基于贝叶斯结构学习的航班保障Petri网构建

2020-08-01邢志伟陈丰华

中国民航大学学报 2020年3期

邢志伟，陈哲，夏欢，罗谦，丛婉，陈丰华

（1.中国民航大学电子信息与自动化学院，天津 300300；2.中国民用航空局第二研究所机场运行与控制工程技术研究中心，成都 610041；3.广州白云国际机场股份有限公司信息科技部，广州 510410）

近几年民航运输业高速发展，截至2017 年旅客吞吐量达千万级的机场已有32 个，以2 月份全球机场放行准点率为例，其中，国内放行准点率最高机场为大连国际机场，准点率80.89%，相比于日本伊丹机场95.13%的放行准点率有较大差距。地面服务保障低效是造成放行准点率低的主要原因之一。目前，中国民航局力推建设机场协同决策支持系统A-CDM 有望解决此难题，A-CDM 通过获得精确的撤轮档时间来提高地面服务保障的效率，实现机场与空管、航空公司共同规划合理的航班放行顺序，从而提升航班正常放行率，保障机场航班高效运行。

针对航班保障服务流程的相关研究有：文献[1]利用关键路径还原的方法刻画航班保障流程；文献[2]针对陆侧服务环节建立数学模型表示航班静态流程；文献[3]首次提出利用Petri 网描述航班保障流程；文献[4]利用Petri 网对不同的保障过程建立了机坪作业任务流程图；文献[5]利用Petri 网刻画航班保障计划流程，通过蒙特卡罗算法预测撤轮档时间，但为提高精度代价过大。

为准确预测撤轮档时间，必须预测保障过程中各关键节点的时间。因此，基于历史数据得到真实的航班保障节点的网络结构是解决准确预测各保障环节时间的关键。文献[6]提出了最大最小爬山（MMHC,maxmin hill climbing）算法，该算法自提出以来得到了广泛的应用，但在航班保障结构学习场景中，需要对边进行反转操作，破坏了各业务环节的先后顺序，导致预测的撤轮档时间与实际结果偏差较大。K2 算法是一种结合先验信息的搜索算法，在考虑先验节点顺序的前提下，避免了前后节点顺序颠倒的情况，保证在符合实际保障执行过程的网络结构基础上，预测撤轮档时间更加准确。

综上所述，利用贝叶斯结构学习K2 算法，从保障数据中确定关键节点的网络结构，通过时间复杂度和搜索空间两个评价指标证明基于父子库所的航班保障K2 算法的合理性，为了精准描述航空器在保障流程中的状态切换，提出了基于贝叶斯网络的无环Petri网关键节点的网络结构。通过对比实验的评分结果，说明从数据中确定网络结构较航班保障的计划流程网络更能反映真实的保障执行过程。

1 基于贝叶斯网络的Petri 网

1.1 保障业务流程

过站航班地面服务，从上轮档到撤轮档的过程中一共包含20 个业务环节。按照各业务环节的依赖关系将上轮档到撤轮档之间的业务环节分为机务巡检、客舱服务、货舱服务及加航油4 个并行的业务流程。各服务流程包含多个子环节，完整的航班计划保障服务工作流程如图1 所示。

图1 航班保障服务流程Fig.1 Flow chart of flight support

上述保障流程是按照业务环节的先后顺序得到的计划执行过程，在实际保障过程中高峰时段因机场保障资源有限，航班保障服务的各业务环节的执行顺序会发生变化，导致航班计划保障流程不能正确反映实际的航班保障过程。因此，只有从实际数据中确定真实的航班保障流程，才能准确描述保障环节的执行过程。

在航班保障流程中，机务巡检和加航油的时间窗口较大，且不影响客、货舱服务流程。客舱服务流程中，首先要进行廊桥/客梯车对接，再进行开客舱门和旅客下机，在此将开客舱门和旅客下机视为同一环节。完成此环节后，在并行开展的4 个环节中，只有客舱清洁开始和完成在客舱内部进行，且影响之后的保障环节。货舱服务流程中，开货舱门完成后，其他的保障环节才能依次进行。

综上所述，在航班保障流程中，将上轮档、廊桥/客梯车对接、开货舱门、开客舱门、客舱清洁开始及完成这6 个保障环节定义为关键节点。其余保障环节在满足串行关系和并行关系的业务前提下，网络结构会随着6 个环节的确定而确定。此6 项环节的网络结构将直接决定航班保障流程的网络结构。

1.2 贝叶斯网络的无环Petri 网

贝叶斯网络[7]用一个有向无环图描述了节点（也称作变量）之间的依赖关系，如果节点X 到节点Y 有一条边，那么称X 为Y 的父节点，而Y 为X 的子节点，将父节点视作原因，子节点视作结果，贝叶斯网络即为从原因到结果的推理过程。Petri 网[8]中S 表示库所，代表实物的状态。实物标识由一个库所传入下一个库所，可看作实物由状态1 切换到状态2，利用贝叶斯网络可以将前一个库所代表的状态视为父状态，后者为子状态。在航班保障流程中，实物代表需要进行保障的航班，上轮档到撤轮档的业务流程看作由父状态到子状态的发生过程。每个业务环节的发生都以父状态的发生为前提，如上轮档环节发生导致机务巡检、廊桥/客梯车对接、开货舱门、加航油发生，开货舱门业务环节完成才能进行装卸货物的业务操作。因此，从上轮档到撤轮档的过程，可以利用一种基于贝叶斯的Petri 网进行描述。

由以上论述及贝叶斯是无环图的设定，定义一种基于贝叶斯网络的无环Petri 网，用于描述航班保障流程。

定义1Σ=（S，T，F）为一个纯网[9]，沿任意有向弧方向的变迁序列δ =（δ1，δ2，…，δl），若∀ti，tj∈δl，tu∈T，∀sk，sm∈S，sk∈·tj且sk∉tj·，sm∈·tu且sk∈tu·，sm为sk的父库所，sk为sm的子库所，记为sm=π（sk），sk=D（sm），则称Σ为贝叶斯无环Pertri 网。其中：S、T、F 分别代表Petri 网中库所集，变迁集和有向弧集，l，i，j，u，k，m∈N+，·tj表示变迁tj所有输入库所的集合，ti·表示ti所有输出库所的集合，·tu与tu·同理。

利用上述定义的网络，构造航班保障关键节点网络，如图2 所示。

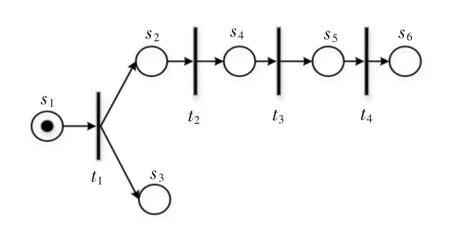
图2 航班保障关键节点的贝叶斯无环Petri 网（计划流程）Fig.2 Bayesian acyclic Petri net of flight support key node（planned flow）

库所与保障环节对应关系如表1 所示。

表1 库所与保障环节对应关系Tab.1 Place and flight support task

由定义1 知，s1=π（s2），s1=π（s3），s2=π（s4），s4=π（s5），s5=π（s6），对应航班保障流程因果关系为上轮档是廊桥/客梯车对接和开货舱门的父状态，开客舱门为廊桥/客梯车对接的子状态，客舱清洁为开客舱门的子状态。所有的子状态只有在父状态完成的情况下才能进行，这也符合航班保障业务环节的先后顺序。由此可看出，贝叶斯无环Petri 网既可以描述航空器在不同保障环节的所处状态，又能够以因果关系描述保障节点之间的依赖关系。

2 航班保障关键节点K2 算法模型

2.1 模型建立

图2 中关键节点流程是基于业务环节先后顺序计划的流程，真实情况的网络结构要从历史数据中确定，才能真实还原航班保障关键节点的网络结构。采用贝叶斯结构学习K2 算法从数据中确定真实情况的关键节点的网络结构。

贝叶斯网络中的K2 算法[8]是最早的贝叶斯结构学习算法之一，算法的目的是在已知先验节点顺序ρ 和最大父节点个数u 的前提下，寻找CH 评分函数最高的网络结构，基于变量Xi、其父节点π（Xi）及之间的边形成的局部结构的CH 评分函数，表示如下

其中：D={D1，D2，…，Dm}为完整的数据集，Di∈D；Xi共有ri个取值1，2，…，ri；其父节点π（Xi）的取值共有qi个组合，则其最大值为表示数据集D 中满足Xi为第k 个节点，π（Xi）为第j 个节点的样本数量，即mijk不超过m。

在航班保障流程中，以库所si及父库所π（si）作为算法中的变量Xi及其父节点π（Xi），代入式（1）得到基于父子库所的航班保障关键节点K2 算法CH 评分函数，即

则航班保障关键节点网络的利用CH 评分选择最优网络结构G 的表达式为

其中：n 为航班保障关键节点数。

在航班保障网络中，各业务环节按照串并行的关系连接成网络结构图，因此，在航班保障网络中，不存在孤立节点，即对于任意保障环节满足如下条件

转换为贝叶斯无环Petri 网的形式为

综上所述，航班保障关键节点的贝叶斯结构学习模型如下

从K2 算法CH 评分函数的角度，网络中出现孤立节点是由于加入该节点后，不再使CH 评分增加，所以为了满足约束条件，只能在节点排序ρ 中，寻找使得评分函数损失最小的节点作为孤立节点的父节点。基于父子库所的航班保障关键节点K2 算法的伪代码如下。

2.2 时间复杂度分析

在流程图中，假设式（2）需要的阶乘结果已经储存在计算机中，保障环节取值状态最大为r，则第4 行CH 评分函数的时间复杂度为O（mr）；第6 行在第4行的基础上最多计算n 次，所以时间复杂度为O（mnr）；if 循环的最多执行u 次，因此while 循环的时间复杂度为O（mnur）；for 循环需要执行n 次，因此关键节点K2算法的时间复杂度为O（mn2ur）。贪心算法时间复杂度[8]为O（mn2r2n）。存在如下性质。

性质1假设m 为样本数量，n 为航班保障关键节点数，u 表示最大父库所个数，r 是节点取值状态的最大值，满足m，n，r，u∈N+，1≤u ＜n，那么mn2r2n＞mn2ur。

证明要证mn2r2n＞mn2ur，即证2n＞u，说明样本数量和取值状态不影响两者大小的比较。由于n，u∈N+，1≤u ＜n，所以2n＞u，即mn2r2n＞mn2ur。证毕。

性质1 说明K2 算法计算局部父子节点评分的方法将指数级的时间复杂度降低为多项式时间复杂度。

2.3 搜索空间分析

贝叶斯网络结构的搜索空间[10]为

这是利用贪心算法在全局范围内搜索最优网络的结构学习算法的可行域。在某一特定排序下，航班保障关键节点的搜索空间为同样存在如下性质。

性质2n 为网络节点数，满足n∈N+，那么，f（n）=

证明令要证命题成立，即证g（n）≥0。

数学归纳法

当n=k+1，则

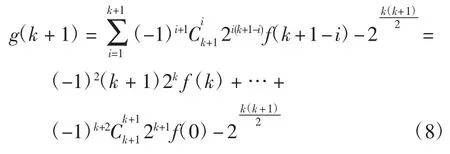
又k+2≥k+1-i，i≥1 则

即n=k+1 时，命题成立，则原不等式成立。证毕。

性质2 说明，加入节点排序缩小了贝叶斯网络结构的可行域。代入数值验证，在含有6 个节点的贝叶斯网络中，贪心算法的搜索空间为算法的搜索空间仅为可从数值上直观地看出加入节点排序，极大地缩小了搜索空间。

3 实验分析

使用国内某枢纽机场的航班保障数据，选取早高峰时段的3U8741 航班上轮档、廊桥/客梯车对接、开货舱门、开客舱门、清洁开始、清洁完成6 个保障关键环节的数据进行实验，利用K-means 聚类算法对各环节的时间数据聚类。将每个聚类时刻的类别作为各变量的取值，再将数据处理为矩阵形式，其中行代表6 个保障环节，列代表一天完整的各环节的数据。先验的节点排序为ρ=[1 2 3 4 5 6]，节点序号依次代表上轮档、廊桥/客梯车对接、开货舱门、开客舱门、清洁开始、清洁完成。

设最大父库所个数u=3。将数据矩阵、节点排序ρ 和u 输入航班保障关键节点K2 算法。算法通过CH评分输出6 个保障环节的网络结构，图3 为最终结果。表2 为存在父子结构节点的CH 评分。

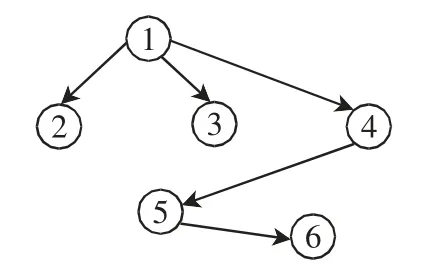
图3 基于K2 算法的航班保障关键节点网络结构Fig.3 Key node network structure of flight support based on K2 algorithm

表2 CH 函数评分结果Tab.2 CH scores

选取贪心爬山类搜索算法中应用较为广泛的爬山（HC,hill climbing）算法、最大最小爬山（MMHC）算法及父子关系（PC, parents children）算法作为对比方法。实验结果如图4 所示。

图4 3 种对比算法的实验结果Fig.4 Experimental results of three algorithms

这3 种算法在搜索过程中，没有利用先验知识，只依评分函数对可能的网络结构进行打分，并将得分最高的结果作为网络的最终结构。从图3 可看出：在没有引入先验节点顺序的条件下，HC 与MMHC 算法将没有前后约束关系的开货舱门环节作为廊桥/客梯车对接的父节点，在数据记录中两者在执行过程中的前后顺序不能作为贝叶斯网络中的因果关系；PC 算法在模型优化过程中，加入了转边操作，如果网络评分大于翻转前的网络评分，则选取该网络结构作为优化网络模型，因此，在PC 算法的实验结果中，清洁完成环节作为清洁开始环节的父节点。在航班保障流程中，清洁开始一定在清洁结束前完成，转边操作虽然提高了评分函数值，但是违反了保障环节的执行顺序，所以不能应用在航班保障结构学习的场景中。利用汉明距离对实验结果进行评价，如表3 所示。

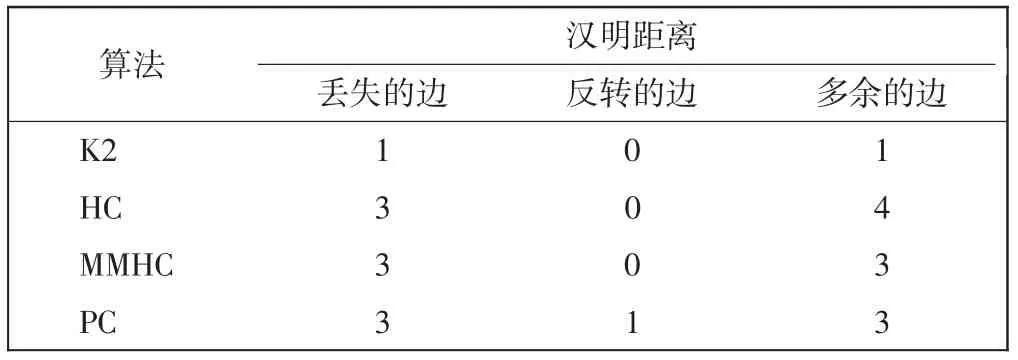
表3 4 种算法结果与计划网络的汉明距离Tab.3 Hamming distances between plan net and four algorithms

从表3 可看出，3 种仅仅根据数据评分的对比算法与计划网络的汉明距离较大。利用定义1 刻画6 个保障环节关键节点，如图5 所示。

图5 航班保障关键节点的贝叶斯无环Petri 网（实际流程）Fig.5 Bayesian acyclic Petri net of flight support key node(actual flow)

对比图2 的航班计划保障流程，开客舱门在廊桥对接之后，而从数据中确定的保障流程，两者是并行关系。

图5 中，s2、s3、s4与s1组成的并行结构评分为CH（〈（s2、s3、s4），s1）〉|D)=-113.871 0。而图2 中，按照计划保障流程，开客舱门与廊桥/客梯车对接、上轮档及开货舱门环节组成的局部网络G*评分值为CH（G*|D）=-225.413 5。对比两者评分结果可看出，从数据中得到开客舱门、廊桥/客梯车对接、开货舱门与上轮档组成的并行结构的网络评分优于计划网络中4个环节组成的网络结构评分。

为保证实验结果的可靠性，在同一时间区间内，随机选取不同时段的3 个过站航班：CZ330 航班的保障任务在下午进行，3U8205 的保障任务在晚上进行，9C8563 为凌晨到达该机场的过站航班。同样将3 个航班的关键节点数据处理为矩阵形式输入航班保障关键节点K2 算法，均得到图3 的实验结果。其中，开客舱门、廊桥/客梯车对接、开货舱门及上轮档组成的并行结构的局部评分与计划保障网络中4 个环节的网络结构的评分结果如表4 所示。

表4 不同航班的4 个保障环节对应两种网络结构的CH 评分Tab.4 CH scores of four support tasks corresponding to two network structures of different flights

在可靠性实验中，上述4 个环节的局部网络评分均优于计划保障网络的评分。说明在实际的航班保障流程中，记录的廊桥/客梯车对接时间为此环节完成的时间，而开客舱门环节在廊桥/客梯车对接完成之后立即执行。因此在历史数据方面，两者记录的时刻几乎相同，通过贝叶斯结构学习得到并行的网络结构。在客舱服务流程中，如果利用计划流程作为实际的网络结构预测各保障环节的开始和执行时间，那么后续环节将廊桥/客梯车对接时间纳入统计时间内，造成串行环节时间预测的偏差。实验结果证明基于历史数据确定航班保障流程网络结构的方法，更能反映真实情况。