基于Chebyshev配置点谱方法的多孔介质平板通道内的流体流动数值模拟

李 斌，李本文，2，陈元元，许学成

(1.武汉科技大学材料与冶金学院，湖北 武汉，430081；2.大连理工大学能源与动力学院，辽宁 大连，116024)

多孔介质内流体的自然对流现象广泛存在于自然界及工程技术领域，近几十年来，国内外众多研究者通过实验、理论分析和数值模拟等围绕该现象展开了大量研究。多孔介质结构具有很强的随机性、复杂性，得益于计算机技术的不断发展，研究者常采用数值方法来研究其中的流动问题。如Kaviany[1]采用有限差分法模拟了等温平板间多孔通道中的层流流动，通过引入多孔介质形状参数γ，分析了γ在极限范围(0，∞)内对多孔介质通道流体的速度分布及压力损失的影响。Nithiarasu等[2]采用有限元法模拟了变孔隙率条件下多孔介质中流体的等温流动，利用半隐式时间离散格式并结合速度修正方法推导出瞬态多孔介质中流场的动量方程。杨勃等[3]采用有限容积法模拟多孔介质通道内的流体流动过程，研究了不同孔隙率下流场的变化规律。常焕静[4]采用有限差分法分别模拟了水和幂律流体在多孔介质中的流动，并分析了多孔介质不同的排列方式及颗粒直径对流体的压降和阻力系数的影响。需要指出的是，有限差分法、有限元法和有限容积法等经典数值方法虽然在针对多孔介质内流体流动特性的研究中运用比较广泛，但它们均为低阶收敛方法，相比之下，谱方法具有指数级收敛精度且易实施、稳定性好[5]，因而应用前景广阔。本课题组基于Chebyshev-Fourier配置点谱方法已稳定地求解了圆柱坐标系下三维瞬态Navier-Stokes方程[6]，并采用Chebyshev配置点谱方法成功模拟了方形多孔腔内的自然对流问题[7-9]。在数值研究中，往往易忽略模型入口段长度和边界层厚度，导致速度分布和传热计算产生严重误差，因此，在本课题组前期研究基础上，本文基于Chebyshev配置点谱方法借助MATLAB模拟多孔介质平板通道内的流体流动特性，并对程序可靠性进行验证，重点探讨达西数(Da)、雷诺数(Re)及孔隙率(ε)对流体流动速度分布、边界层厚度及入口长度的影响。

1 物理与数学模型

以典型的多孔介质平板通道流动模型为研究对象，图1所示为2维轴对称多孔介质平板通道流动物理模型，其高度为H/2，长度L为2H，流体以速度u(y)进入通道，平均速度为u0。

·V=0

(1)

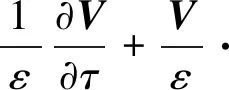
(2)

τ=0,0≤X≤2,0≤Y≤0.5∶U=V=0

(3)

(4)

其它边界条件如压力等见计算方法部分。

2 计算方法

2.1 时间离散

首先采用准隐式格式[12]对动量方程(式(2))进行时间离散，其中时间导数项采用二阶向后差分格式，压力项、扩散项和源项均采用隐式格式，对流项采用显式Adams-Bashforth格式，则式(2)可离散为

(5)

式中：τs为无量纲时间步长；n-1、n和n+1表示时间离散级数。

2.2 改进的投影算法

采用由Hugues等[13]提出的IPS(improved projection scheme)处理速度场和压力场的耦合求解问题，执行步骤如下：

(1)压力预估步，求解预估压力P*。对式(5)两边取散度并用连续性条件限制，得到预估压力泊松方程

ΔP*=

(6)

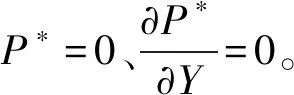
(7)

式中：n表示边界的法向量。

为了提高稳定性，将拉普拉斯算子分解为一个螺旋矢量场和一个无旋矢量场[14]，并用连续性条件限制后得到

2ΔVn-ΔVn-1=-2××Vn+××Vn-1

(8)

(2)速度预估步，求解预估速度V*。根据P*和式(5)，获得亥姆霍兹方程

(9)

·Vn+1=0

(10)

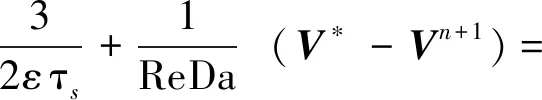
(11)

(12)

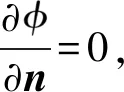
Vn+1=V*-

(13)

(14)

2.3 空间离散

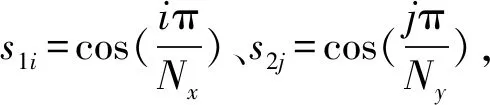
(15)

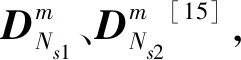
(16)

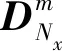
(17)

(18)

式中：T表示矩阵转置。

2.4 系数矩阵的确定

AΦ+ΦB=F

(19)

式中：A、B分别为(Ny+1)、(Nx+1)阶系数矩阵；Φ、F为(Ny+1)×(Nx+1)系数矩阵，Φ表示φ(Xi,Yj)的值。事实上，未知边界向量可以表示为已知边界值和函数内部节点值φ(Xi,Yj)(i=1,2,…,Nx-1，j=1,2,…,Ny-1)的函数关系式，将矩阵方程(19)改写为

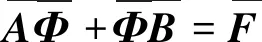
(20)

(21)

式中：hx+,j、gx-,j、hy+,i、hy-,i均为已知边界函数。然后根据离散边界条件和已知边界值可获得未知边界值表达式

(22)

1≤j,k≤Ny-1

(23)

(24)

1≤i≤Nx-1，1≤j≤Ny-1

(25)

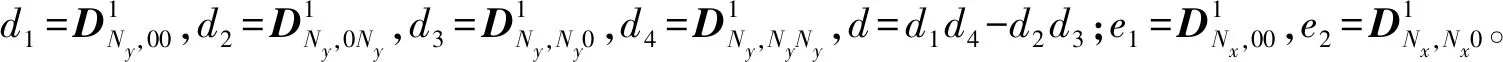
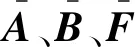
2.5 计算步骤

多孔介质平板通道流动问题求解的计算步骤如下：

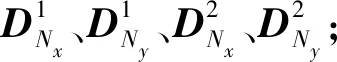
(2)给无量纲变量及各参数赋值，初始化速度场、压力场和中间变量场，并令φ-1=φ0；

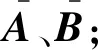
(4)设置收敛标准，开始时间步进；

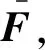
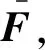
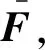
(8)模拟结果如果满足收敛标准就终止循环，否则，推进一个时间步，令φn-1=φn、φn=φn+1，返回步骤(5)；

(9)输出结果。

计算中，取无量纲时间步长Δτ=1×10-6，无量纲速度和无量纲压力的收敛标准分别为‖Un+1-Un‖max<1×10-6、‖Vn+1-Vn‖max<1×10-6、‖Pn+1-Pn‖max<1×10-6。

2.6 网格无关性检验

通过网格加密，考察距离对称轴最近的一条水平网格线上U(Xi,Y1)的分布曲线变化趋势以验证网格无关性。x、y方向的网格节点数(Nx+1)×(Ny+1)从13×4增加到73×19。计算中取ε=0.9、Da=1×10-4、Re=100，检验结果如图2所示。从图2中可以看出，当网格节点数从13×4增加到53×14时，无量纲速度U(Xi,Y1)变化较为明显，继续增加网格节点数，无量纲速度U(Xi,Y1)几乎不再变化，表明网格节点数为53×14时数值解满足网格无关性要求，故而，在本文后续计算中x、y方向的网格节点数取53×14。

图2 网格无关性检验

2.7 程序验证

不同γ条件下，流体在多孔介质平板通道出口速度分布以及在充分发展区域最大速度的精确解表达式[1]分别为

U|X=2=[1-e-2γ-(1-e-γ)(eγ(Yj-1)+e-γYj)]×

[1-e-2γ-2(1-e-γ)2γ-1]-1

(26)

(27)

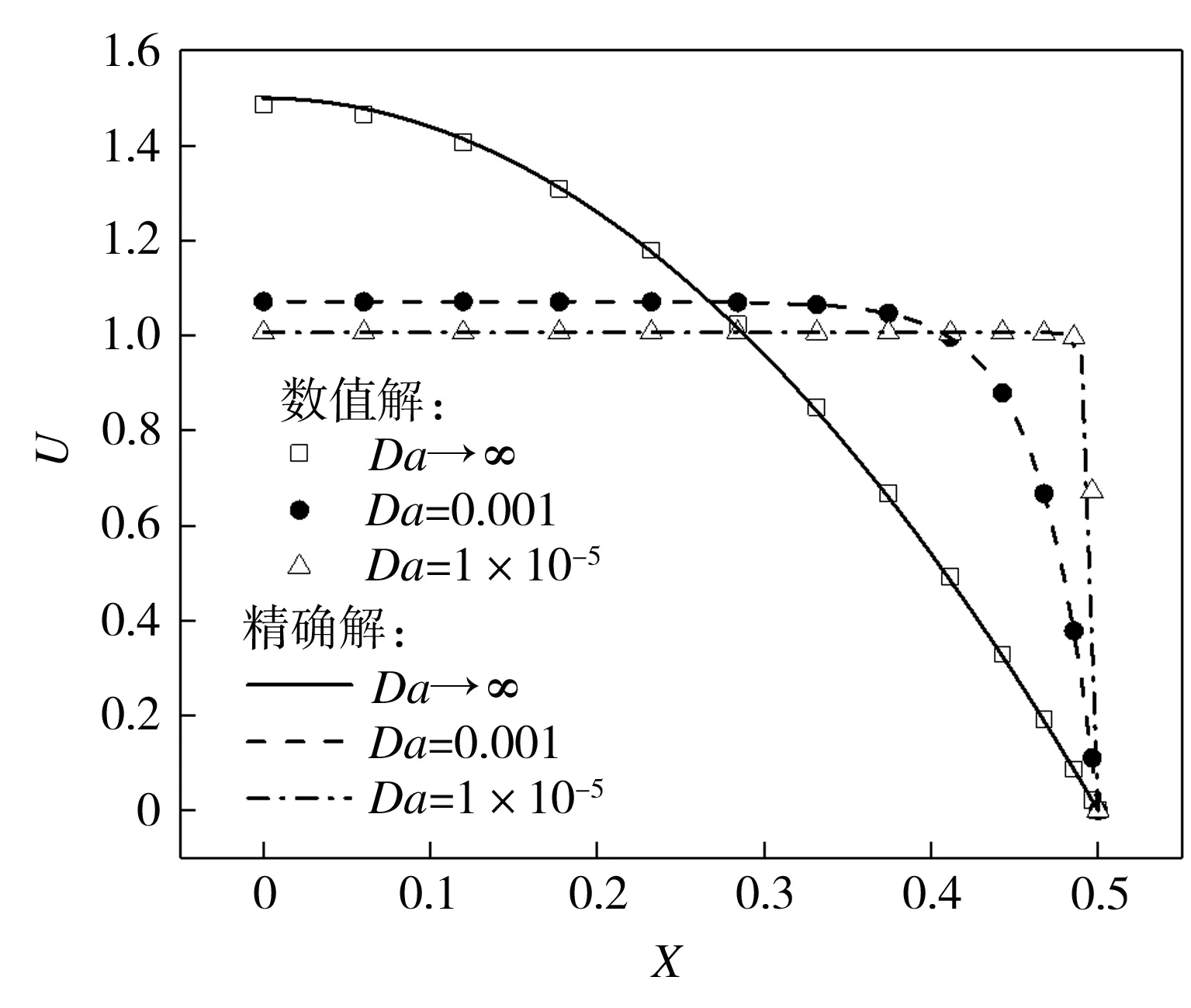
(a) U

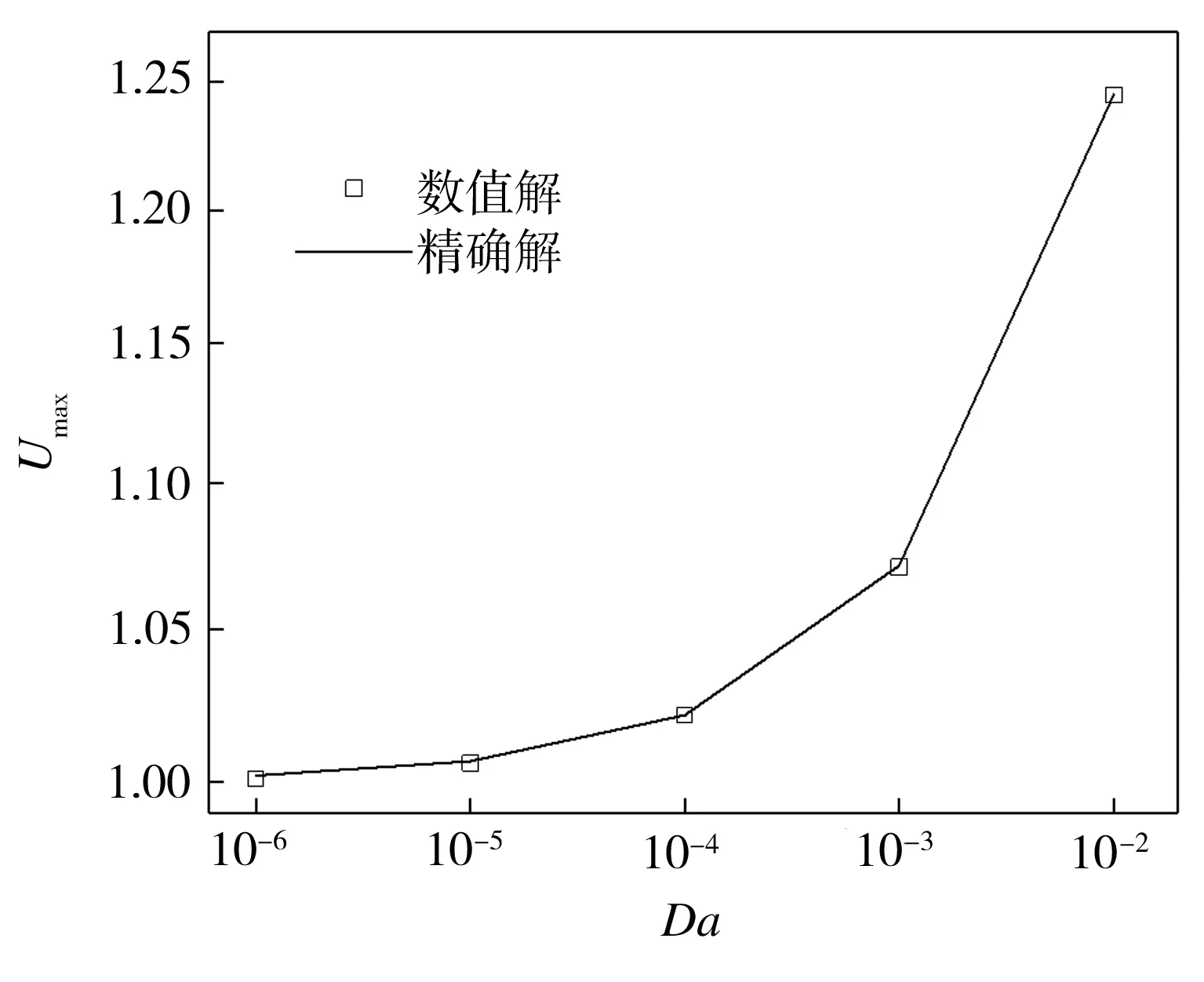
(b) Umax

3 结果与分析

3.1 流体速度分布

当ε为0.9、Da为1×10-4、Re为100时，流体在多孔介质平板通道内沿来流方向不同截面处的无量纲速度分布如图4所示。由图4可见，沿着来流方向，由于多孔介质的弥散作用，近壁面处的速度梯度迅速增大，当X趋近于0.590时，除贴近壁面的极短区域外，其它区域的流体速度分布接近于常数值。

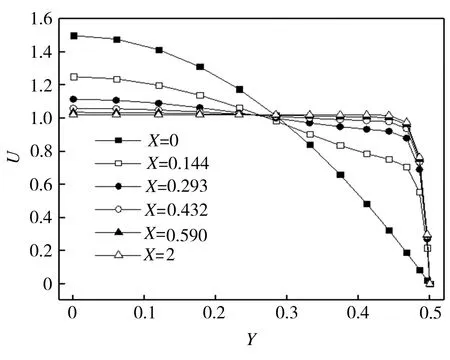
图4 流体速度分布

3.2 Da对多孔介质平板通道内流体流动的影响

当ε为0.9、Re为100时，在不同Da条件下，多孔介质平板通道中的流体在出口(X=2)和对称轴(Y=0)上的无量纲速度分布如图5所示。根据图5模拟结果，可求得不同Da条件下，多孔介质平板通道流体流速在充分发展区域出口处的无量纲边界层厚度δ和入口长度xe如表1所示。结合图5和表1可知，随着Da的减小，近壁面处流体速度梯度逐渐增大，无量纲边界层厚度δ及入口长度xe不断减小，但当Da<1×10-4时，继续减小Da，δ及xe均不再有明显变化。

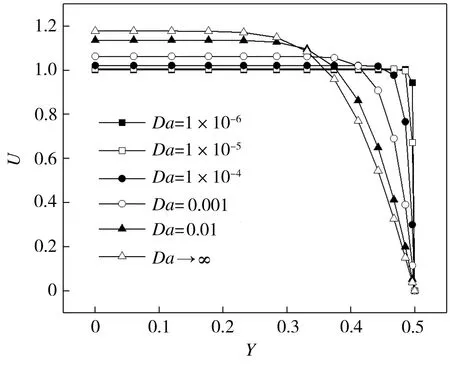
(a) 出口

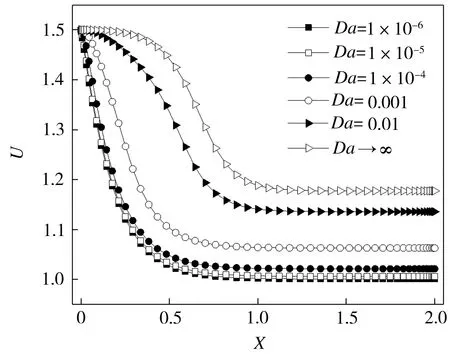
(b) 对称轴

表1 不同Da时多孔介质平板通道流边界层厚度和入口长度

3.3 Re对多孔介质平板通道内流体流动的影响

当ε为0.9、Da为0.01时，在不同Re条件下，多孔介质平板通道中的流体在出口和对称轴上的无量纲速度分布如图6所示，并根据图6模拟结果，求得相应条件下多孔介质平板通道流在充分发展区域出口处的速度边界层厚度δ和入口段长度xe如表2所示。结合图6和表2可以看出，随着Re的增大，多孔介质平板通道流体在充分发展区域出口处的速度边界层不断变薄，而入口段长度相应增大。

(a) 出口

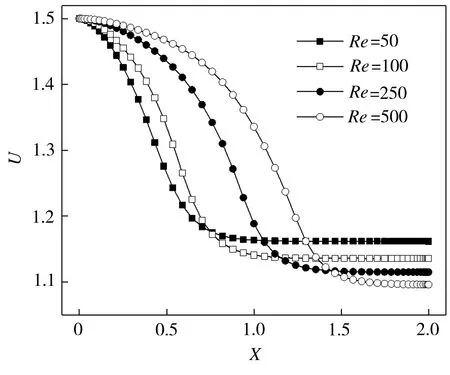
(b) 对称轴

表2 不同Re时多孔介质平板通道流的边界层厚度和入口长度

3.4 ε对多孔介质平板通道内流体流动的影响

当Da为0.01、Re为10时，在不同ε条件下，多孔介质平板通道中的流体在出口和对称轴上的无量纲速度分布如图7所示，相应条件下多孔介质平板通道流体在充分发展区域出口处的速度边界层厚度δ和入口段长度xe的计算结果列于表3。结合图7和表3可知，随着ε的减小，多孔介质平板通道流体在充分发展区域出口处的速度边界层厚度及入口段长度均呈现出增加趋势。

(a) 出口

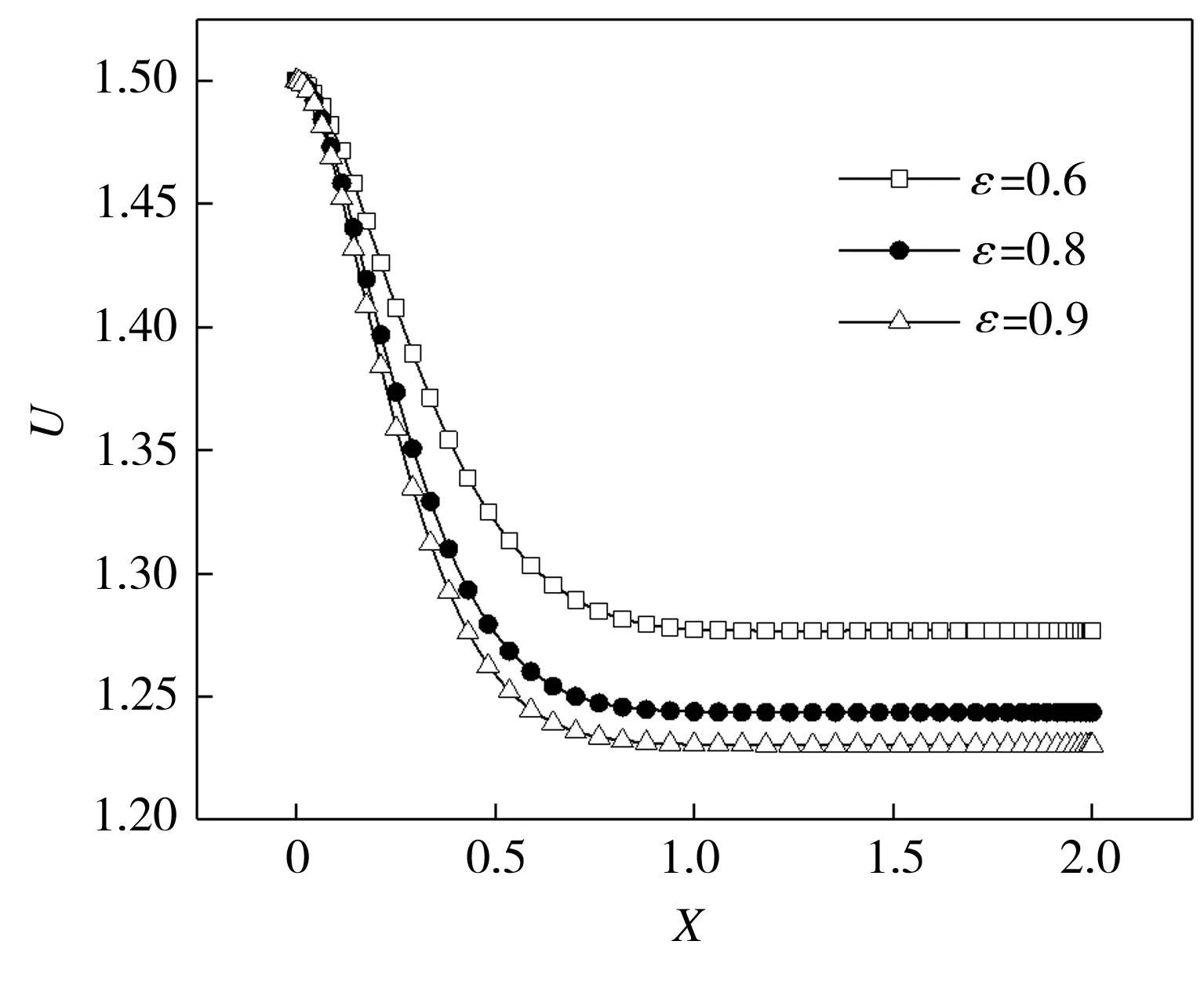
(b) 对称轴

表3 不同ε时多孔介质平板通道流边界层厚度和入口长度

4 结语

本文基于Chebyshev配置点谱方法，借助MATLAB利用数值模拟分析了多孔介质平板通道内流体流动的问题。针对动量方程的离散，空间上和时间上分别采用Chebyshev配置点谱方法和准隐式格式离散，同时采用IPS处理速度场和压力场的耦合求解问题。将数值模拟结果与精确解进行比较，发现两者具有很好的一致性，这证实了使用Chebyshev配置点谱方法求解该类问题有效可行。同时，数值模拟还发现，达西数(Da)、雷诺数(Re)及孔隙率(ε)对多孔介质平板通道流体在充分发展区域的速度边界层厚度和入口长度具有明显影响作用：当其它条件确定时，速度边界层厚度和入口长度随着Da的减小而减小，但当Da减小到1×10-4以下时，这些变化不再明显；随着Re的增大，速度边界层厚度不断变薄，入口长度逐渐增大；速度边界层厚度和入口长度随着ε的减小均呈现出增大趋势。本文研究结果为今后进一步研究多孔介质内流体的流动、换热与燃烧问题提供了参考。