基于遗传算法的混合流水车间调度问题研究
2020-08-01林飞龙王晓晨
林飞龙,陶 泽,王晓晨
(1.沈阳理工大学 机械工程学院,沈阳 110159;2.大连海事大学 航运经济与管理学院,辽宁 大连 116026)
近年来,越来越多的学者开始进行调度问题的研究[1]。国内外对于车间调度优化问题也提出了较多的解决方案[2-5]。企业为提高生产效率、增加收益,优化车间调度无疑是最好的方法之一。车间调度问题目前已被证明是NP-complete问题[6],在实际研究过程中需要考虑很多因素,所以至今为止仍没有形成一套完整系统的理论。
杜利珍等基于果蝇优化算法求解不相关并行机混合流水车间调度问题,并采用标杆实例进行仿真实验,验证了算法的有效性[7]。陶泽等提出小生境遗传算法解决双目标混合流水车间调度问题,并通过仿真实验得出最优方案[8]。Fernandez-Viagas V等针对解决混合流水车间调度问题,比较了20种启发式算法,并提出了两种基于记忆的构造性启发式算法来求解置换flowshop调度问题[9]。Zhong W等研究了两阶段无等待混合流水车间环境下调度算法的性能,该环境具有阶段间灵活性,每个阶段有多台并行机[10]。本文对具有并行机的混合流水车间进行研究,并与EDA[11]遗传算法和SFLA[12]遗传算法进行对比分析,进一步验证本文算法的有效性和鲁棒性。
1 问题描述
相对于流水车间(FSP)调度问题,混合流水车间(HFSP)调度不仅要解决工件的加工顺序且要解决并行机的分配问题。HFSP调度可描述为:n个工件在M台机器上进行加工,如图1所示。各个工件的加工顺序相同,至少有一道工序存在并行机,需要确定工件在哪台机器上加工能够使加工时间最短。

图1 Flow Shop调度的结构
构建具有并行机的混合流水车间调度的数学模型,主要包括工件约束、加工设备能力约束、工艺顺序约束,计算原理如下所示。
xi1为0-1变量(若工件i被安排在第1个位置则取值为1,否则取值为0);
yijk也为0-1变量(若工件i的第j道工序被安排在第k台机器上取值为1,否则取值为0);
sij表示工件i的第j道工序的开始加工时间;
eij则表示工件i的第j道工序的完成时间。
eij=sij+tij,i=1,2;j=1,2,
eijsi(j+1),i=1,2;j=1,2,

j=1,2,…,m
2 遗传算法求解
由于混合流水车间调度问题已经被证明是NP完全问题,所以本文将基于遗传算法对HFSP调度问题展开研究。应用遗传算法求解的一般流程如图2所示。
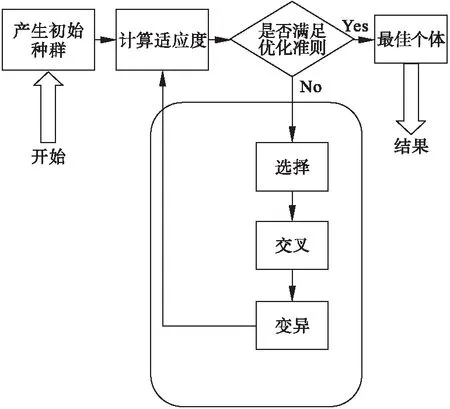
图2 遗传算法的流程图
2.1 编码方法
混合流水车间的编码方式采用基于工件的编码方式。例如用vk=[1,2,3]来表示第k个染色体,工件的加工顺序为:J1、J2、J3。本文讨论的HFSP调度问题,每一加工工序上并行机的加工性能不同,即同一工件在同一工序不同机器上的加工时间不同。
解码规则是依据最小化完工时间,通过计算若在闲置机器M1上加工的完工时间小于工件在正在工作的并行机所需的加工时间与等待时间之和,则在M1上进行加工,反之工件在M2上进行加工,具体示例如下所示。
假定现有3个工件J1、J2、J3依次三道工序进行加工,机器的编码以及并行机的分布情况如图3所示,工件在各个机器上的加工时间为:M1(2,5,3)、M2(5,4,2)、(6,2,5)、M4(2,1,3)。随机产生的染色体为{1,3,2}。

图3 FSP调度的机器编号
(1)工序1:T(1,1)=2,T(3,1)=3,T(2,1)=5。
(2)工序2:T(1,2)=5,T(3,2)=2,T(2,2′)=2;T(1,2)+T(1,1)=7;T(1,1)+T(1,2)+T(3,2)=9;T(1,1)+T(3,1)+T(2,1)+T(2,2′)=12。
(3)工序3:T(1,3)=2,T(3,3)=3,T(2,3)=1;T(1,2)+T(1,1)+T(1,3)=9;T(1,1)+T(1,2)+T(3,2)+T(3,3)=12;T(1,1)+T(3,1)+T(2,1)+T(2,2′)+T(2,3)=13。
2.2 初始种群
初始种群通过计算机随机产生。然后按照一定的方法选择相对较优的个体作为子代,淘汰适应度值相对较低的个体,保证方案向着最优转化。
2.3 适应度函数
用Cmax表示第k个染色体的最大完工时间,那么适应度函数为
F(k)=1/Cmax
2.4 遗传算子的设计
(1)选择算子
按每个个体的适应度函数值大小排名,选出较好的染色体个体,淘汰排名靠后的个体。
(2)交叉算子
首先选取父代染色体1和2,随机产生一个与染色体长度相同的向量,由数字1、2组成。向量定义了由父代1、2中选取基因的顺序,从向量所指定的父代中选取基因并从另一个父代中消除对应的基因,重复该步骤,直到两父代染色体为空且子代包含所有染色体为止。如父代1表示加工工件的数目为10个,且加工时优先考虑加工工件的顺序为J1、J2、J4、J6、J8、J7、J5、J3、J0、J9。随机产生一个与染色体长度相同的向量,由数字1、2组成。
父代1:1 2 4 6 8 7 5 3 0 9;
父代2:1 0 2 4 6 3 9 7 5 8。
随机产生的数字:1 1 2 1 2 2 1 1 2 2。
交叉结果:
子代1:1 2 0 4 6 3 8 7 9 5;
子代2:1 0 2 4 6 8 3 5 7 9。
(3)变异算子
遗传算法中的变异运算,是指将个体染色体编码串中的某些基因用该基因座的其他等位基因来替换,从而形成一个新的个体。本文使用逆序变异算子,如下例所示。
染色体:1 2 04 6 3 87 9 5;
变异后:1 2 08 3 6 47 9 5。
(4)终止条件
取总的繁衍代数为终止条件。
3 仿真实验及结果分析
3.1 仿真案例1
为验证算法的可行性,本文将应用Matlab对HFSP调度进行实例分析。现有10个工件要一次经过9道工序进行加工,其中第8道工序上有两台机器,且其加工性能不完全相同。
设个体数目NIND=40,交叉概率为XOVR=0.8,变异率为MUTR=0.01。最大遗传代数GENmax=200。
这里用矩阵R表示各工件在各个工序上的加工时间。矩阵的每一行表示工件J1、J2、J3、J4、J5、J6、J7、J8、J9、J10在机器M0、M1、M2、M3、M4、M5、M6、M7、M8、M9上的加工时间。

3.1.1稳定性分析
本次实施的程序,本文通过应用软件进行50次模拟仿真,对比所得数据,进行软件稳定性分析。所得数据如表1所示。

表1 仿真结果 min
由表1可以看出,程序稳定性良好,其中非最优解115与最优解的误差为0.88%,且在50次仿真中只出现3次,而非最优解117的误差为2.63%,但在50次仿真中只出现1次,故认为程序误差在可接受范围内。
3.1.2改变运行参数
在其他参数不变的情况下,对交叉概率为XOVR=0.8、XOVR=0.7、XOVR=0.6分别各自进行10次仿真模拟,比较得出较优调度方案。
(1)交叉概率XOVR=0.8时,应用Matlab仿真10次结果如表2所示。

表2 XOVR=0.8时的最大完工时间 min
(2)交叉概率XOVR=0.7时,应用Matlab仿真10次结果如表3所示。

表3 XOVR=0.7时的最大完工时间 min
(3)交叉概率XOVR=0.6时,应用Matlab仿真10次结果如表4所示。

表4 XOVR=0.6时的最大完工时间 min
从表2、表3、表4不难看出,当交叉概率XOVR=0.8时,出现了相对较优的结果128min。
当交叉概率XOVR=0.85时,出现的最优结果仍为128min,但其对系统运行效率影响如表5所示。

表5 改变XOVR对系统运行效率的影响
由此可见XOVR取0.8更优。
按照上述方法改变最大遗传代数和个体数目,最终得出相对较优方案为:交叉率XOVR=0.8,最大遗传代数GENmax=200,个体数目NIND=50。
3.1.3运行结果
程序仿真模拟的结果通过甘特图和进化曲线表示,如图4、图5所示。
3.1.4结果分析
本次仿真设定的最大遗传代数为200,即迭代次数为200次。图4直观的体现了每台机器上工件的加工顺序,valmin=114min。其中每台机器加工工件的顺序并不完全相同,第一台机器上工件的加工顺序即按照随机产生的染色体决定工件的加工顺序,根据所设定的加工时间矩阵R,程序将基于加工周期最小的原则,重新考虑每台机器上工件的加工顺序,但必须保证工件经过每道工序的时间在上一工序之后,即保证每一工件的加工顺序完全相同,符合流水加工的特点。
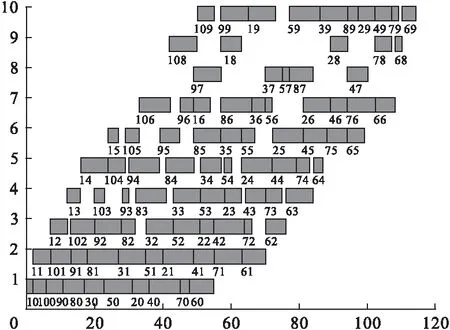
图4 Matlab仿真甘特图
图5直观的体现了在迭代过程中每次迭代产生的最优解的变化以及种群均值的变化,其中种群均值即种群中每一染色体的解求平均值。曲线的起点表示随机产生的初始种群中的最优解,即初始种群中的最佳调度方案。由于初始种群为随机产生,故导致最优解与最差解差异较大,体现在初始阶段两条曲线相差较大,随着遗传代数的增加,种群中的个体逐渐趋于最优化,图5中的两条曲线逐渐趋于重合。

图5 Matlab仿真进化曲线
3.2 仿真案例2
为进一步验证本文算法的有效性和鲁棒性,对文献[11]中的案例进行仿真并与EDA算法和SFLA算法所得的结果进行对比分析,调度结果如表6所示。种群数目NIND=40,交叉概率为XOVR=0.8,变异率为MUTR=0.01。最大遗传代数GENmax=200。

表6 调度结果对比分析
表6表明本文算法取得的最优解优于SFLA方法,运行10次,其中所得解60%优于SFLA所得解;与EDA方法取得的最优解相同,且两者都具有较好的鲁棒性,表明本文所提出的方法确实有效可行。
4 结论
提出基于遗传算法研究具有并行机的混合流水车间的调度问题,解决了混合流水车间n个工件在每台机器上的加工顺序以及工件在并行机上的分配问题。通过Matlab进行仿真模拟所得的甘特图给出最终的调度方案。结果表明,基于遗传算法应用Matlab进行仿真模拟,对混合流水车间的调度问题进行优化,可以很快得出最优解或近似最优解,且易于实现。
