两类图的拉普拉斯谱
2020-07-31李佳建
李 佳 建
(兰州交通大学 数理学院,甘肃 兰州 730070)
近几年,关于拉普拉斯谱的研究取得了一些新的成果。文献[1]得到了H-联图的拉普拉斯特征多项式,给出了H-联图的拉普拉斯谱与图G1、G2、…、Gk之间的关系。文献[2]研究了一致超图的拉普拉斯谱和正规拉普拉斯谱的一些性质。文献[3]刻画了图的字典积的任意幂的邻接谱和拉普拉斯谱。文献[4]利用因子图的谱性质,建立了直积图和强积图的拉普拉斯谱的估计方法。文献[5]和文献[6]讨论了在图的一些乘积运算下拉普拉斯谱的性质。此外,还有一些关于拉普拉斯谱的其他成果[7-12]。
1 基础说明
本文考虑的图都是无向的简单图。设图G的顶点集V(G)={v1,v2,…,vn},边集E(G)={vivj|vi,vj∈V(G)}(vi与vj相邻)。图G的邻接矩阵A(G)=(aij)n×n定义为:若vivj∈E(G),则aij=1;否则aij=0。设λ1≥λ2≥…≥λn为图G的邻接矩阵A(G)的特征值(A(G)的特征值的多重集称为图G的谱,记为Spec(G))。设D(G)=diag(d1,d2,…,dn)为图G的度对角阵,其中di表示顶点vi的度。图G的拉普拉斯矩阵L(G)=D(G)-A(G),其特征值为μ1≥μ2≥…≥μn=0(L(G)的特征值的多重集称为图G的拉普拉斯谱,记为SpecL(G))。
图G与图H的笛卡尔积,记为G□H,其顶点集为V(G)×V(H)={(a,v):a∈V(G),v∈V(H)},顶点(a,v)与(b,w)在G□H中相邻,当且仅当a=b且vw∈E(H),或v=w且ab∈E(G)。设G1i=G1,G2i=G2分别为图G1与图G2的k次复制(1≤i≤k),Gj(j=3,4)为k阶图。2018年,文献[13]首次引入了两种新运算:第一种运算G1■k(G3□G2)是指首先将G3与G2做笛卡尔积,从而产生G2的k次复制G2i,然后将G1i与G2i做联运算G1i∨G2i(i=1,2,…,k)。例如,当图G1=G2=K2、G3=P3时,G1■k(G3□G2)如图1所示;第二种运算(G4□G1)■k(G3□G2)是指首先将G4与G1做笛卡尔积,从而产生G1的k次复制G1i,同时将G3与G2做笛卡尔积,从而产生G2的k次复制G2i,然后将G1i与G2i做联运算G1i∨G2i(i=1,2,…,k)。例如,当图G1=G2=K2、G3=G4=P3时,(G4□G1)■k(G3□G2)如图2所示。受此启发,本文讨论这两类图的拉普拉斯谱。
2 主要结果
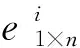
引理1[14]设G1和G2分别为n1和n2阶图,A1和A2分别为G1和G2的邻接矩阵,则G1□G2的邻接矩阵A1□A2=A1⊗In2+In1⊗A2。
引理2[15]设u和v分别为图G1和图G2的属于特征值(或拉普拉斯特征值)θ和η的特征向量。则向量w=u⊗v(ω(x,y)=uxvy)是G1□G2的属于特征值(或拉普拉斯特征值)θ+η的特征向量。
下面给出本文的主要结论。先来刻画图G1■k(G3□G2)的拉普拉斯谱。
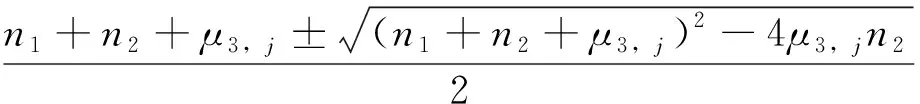
证明:令J为元素全为1的矩阵。对顶点进行适当排列,由引理1可得G1■k(G3□G2)的拉普拉斯矩阵

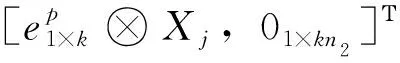
为L(G)的属于特征值n1+r2-λ2,i+μ3,j的特征向量。
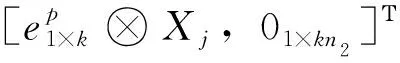
[a111×n1,a211×n1,…,ak11×n1,b111×n2,b211×n2,…,bk11×n2]Τ=[a′⊗11×n1,b′⊗11×n2]Τ。
其中a′=[a1,a2,…,ak],b′=[b1,b2,…,bk],[a1,a2,…,ak,b1,b2,…,bk]≠01×2k。
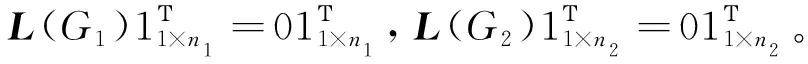
L(G)[a′⊗11×n1,b′⊗11×n2]Τ=ν[a′⊗11×n1,b′⊗11×n2]Τ。
那么,可得到如下含有2k个方程的方程组:
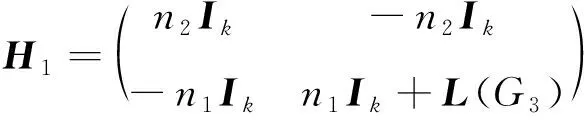
下面讨论矩阵H1的特征值。为此仅需考虑det(νI2k-H1)=0的根。如果ν=n2,由式(1)有bin2=0。但n2>0,从而bi=0。进一步由式(2)可知ai=0。与[a1,a2,…,ak,b1,b2,…,bk]≠01×2k矛盾,从而ν≠n2。故(ν-n2)Ik是非奇异的,即|(ν-n2)Ik|≠0。
注意到
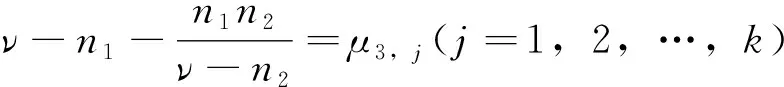
接下来,刻画图(G4□G1)■k(G3□G2)的拉普拉斯谱。
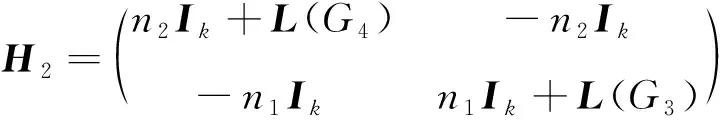
证明:令J为元素全为1的矩阵。对顶点进行适当排列,可得(G4□G1)■k(G3□G2)的拉普拉斯矩阵
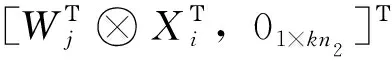

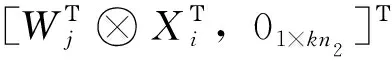
[a111×n1,a211×n1,…,ak11×n1,b111×n2,b211×n2,…,bk11×n2]Τ=[a′⊗11×n1,b′⊗11×n2]Τ。
其中a′=[a1,a2,…,ak],b′=[b1,b2,…,bk],[a1,a2,…,ak,b1,b2,…,bk]≠01×2k。
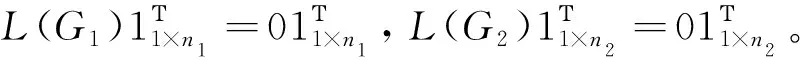
L(G)[a′⊗11×n1,b′⊗11×n2]Τ=ν[a′⊗11×n1,b′⊗11×n2]Τ。
那么我们可得到如下含有2k个方程的方程组
(3)
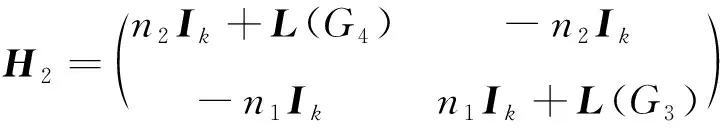
若在定理2中限制G3与G4是两个同构的图,则可得:
推论1 设图Gi为ni阶ri-正则图,且其特征值为λi,1=ri≥λi,2≥…≥λi,ni(i=1,2)并设G3和G4是两个同构的k阶图,则(G3□G1)■k(G3□G2)的拉普拉斯谱是由数
和n1+r2-λ2,i+μ3,j(i=2,…,n2;j=1,…,k)组成的多重集。这里μ3,j(j=1,…,k)是图G3的拉普拉斯特征值。
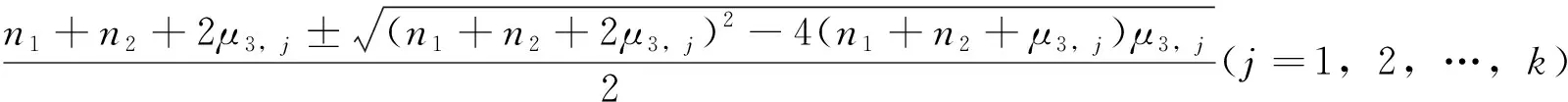

故矩阵H2与H2′相似,从而
|νI2k-H2|
=|νI2k-H2′|

由此得出矩阵H2的2k个特征值为
最后,给出主要结果的两个应用实例。
例1 设Gi=K2(i=1,2),G3=P3,则图K2■3(P3□K2)如图1所示。注意到n1=n2=2,r1=r2=1,图G1、G2的邻接矩阵A(K2)的特征值为λ1,2=λ2,2=-1,图G3的拉普拉斯矩阵L(P3)的特征值分别为μ3,1=0、μ3,2=1、μ3,3=3。由定理1立得图K2■3(P3□K2)的拉普拉斯谱:
SpecL(K2■3(P3□
例2 设Gi=K2(i=1,2),Gj=P3(j=3,4),则图(P3□K2)■3(P3□K2)如图2所示。同理,注意到n1=n2=2,r1=r2=1,λ1,2=λ2,2=-1,μ3,1=0,μ3,2=1,μ3,3=3。由定理2 和推论1可得图(P3□K2)■3(P3□K2)的拉普拉斯谱:


图1 K2■3(P3□K2) 图2 (P3□K2)■3(P3□K2)
3 结 语
一些“简单”的图类在一些图的二元运算作用后可得“复杂”的新图,通过原图的性质刻画新图的相应性质是图谱理论中的重要方法之一。本文针对基于图的笛卡尔积和联运算所构造的两类新图,给出了它们的拉普拉斯谱,并列举了两个应用实例。文中所使用的方法对进一步讨论这两类图的无符号拉普拉斯谱或规范拉普拉斯谱仍有借鉴意义。
