Cartan-Eilenberg绝对clean和level复形研究
2020-07-31张丽英
张 丽 英
(兰州交通大学 数理学院,甘肃 兰州 730070)
Verdier引入了Cartan-Eilenberg(以下简记为CE)投射和内射复形并证明了任意复形G具有CE投射和内射分解[1]。此后,国内外许多学者对CE复形做了进一步研究[2-5]。Bravo等引入了绝对clean模和level模,并由此定义和研究了Gorenstein AC-内射模和Gorenstein AC-投射模[6]。2014年,Bravo等将绝对clean模和level模推广到复形上[7]。2017年,Gillespie对绝对clean模做了进一步研究[8]。受此启发,本文主要研究CE绝对clean复形和level复形。
1 预备知识
以下给出一些基本概念和记号。
定义1[6]称R模F是超有限表示模,如果F具有投射分解…→P2→P1→P0→F→0,其中每个Pi是有限生成投射模。
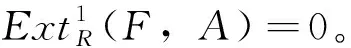

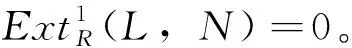

定义5[2]称复形的序列(*)…→C1→C0→C-1→…是CE正合列,如果以下序列均正合:
…→C1→C0→C-1→…
(1)
…→Z(C1)→Z(C0)→Z(C-1)→…
(2)
…→B(C1)→B(C0)→B(C-1)→…
(3)
…→H(C1)→H(C0)→H(C-1)→…
(4)
…→C1/Z(C1)→C0/Z(C0)→C-1/Z(C-1)→…
(5)
…→C1/B(C1)→C0/B(C0)→C-1/B(C-1)→…
(6)
显然(*)是CE正合的当且仅当序列(1)和(2)正合。

定义6[3]称复形的CE正合列0→A→B→C→0是CE纯正合列,如果对于任意的CE有限表示复形P,序列0→Hom(P,A)→Hom(P,B)→Hom(P,C)→0是正合的。
给定一个Abel范畴C,令H是C中的一类对象。记H的右正交为H⊥(H的左正交为⊥H),即H⊥={X|Ext1(H,X)=0,∀H∈H}(⊥H={X|Ext1(X,H)=0,∀H∈H})。称(A,B)是余挠对,如果A⊥=B,且A=⊥B。称余挠对(A,B)是遗传的,如果A关于满态射的核封闭或者B关于单态射的余核封闭。称余挠对(A,B)是完全的,如果它有足够多的投射和内射对象,也就是对于任意的X∈C,存在正合列0→X→B→A→0和0→B′→A′→X→0,其中B,B′∈B,A,A′∈A。
2 Cartan-Eilenberg 绝对clean 和level 复形
除非特别说明,本文中的模均是左R-模。
定义7[2]设F是R-模类。称复形A为CEF复形,如果A、Z(A)、B(A)和H(A)都属于C(F),其中C(F)表示由F中的模构成的复形的全子范畴。
特别地,若F(P,A,L,N)是所有超有限表示模类(有限生成投射模类,绝对clean模类,level模类,cospiral类),则CEF复形就是CE超有限表示(CE有限生成投射,CE绝对clean,CE level,CE cospira)复形。
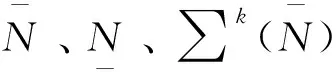

(7)

(8)
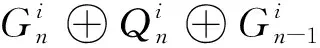

定理1 设A是R-模的复形,则:
(1)A是CE绝对clean复形;
(2)A和Z(A)属于C(A);
(3)B(A)和H(A)属于C(A)。
证明:(1)⟺(2)⟺(3)由文献[6]可知绝对clean模类是余可解的。再根据文献[5]可知结论显然成立。
(1)⟹(4)设A是CE绝对clean复形,X是CE超有限表示复形,则对于任意的CE正合列0→A→U→X→0,有如下正合列
0→An→Un→Xn→0
(9)
0→Zn(A)→Zn(U)→Zn(X)→0
(10)
0→Bn(A)→Bn(U)→Bn(X)→0
(11)
0→Hn(A)→Hn(U)→Hn(X)→0
(12)

考虑如下行正合可裂,列正合的交换图

考虑如下行正合可裂,列正合的交换图
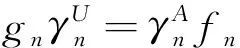
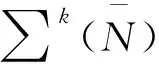
命题1 设R是环,则:
(1)CE绝对clean复形的类关于直和、直积、直和项、正向极限封闭;
(2)CE绝对clean复形的类关于纯子复形和纯商复形封闭;

(4)CE绝对clean复形的类关于CE纯子复形和CE纯商复形封闭。
证明:由文献[6]可知绝对clean模的类关于直和、直积、直和项、正向极限、纯子复形和纯商复形封闭。再根据文献[5]可知(1)、(2)显然。
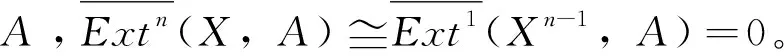

定理2 设L是R-模的复形,则:
(1)L是CE level复形;
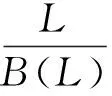
(3)B(L)和H(L)属于C(L)。
证明:(1)⟺(2)⟺(3) 由文献[6]可知level模类是可解的。再根据文献[5]可知结论显然成立。
命题2 设R是环,则:
(1)CE level复形的类关于直和、直积、直和项、正向极限封闭;
(2)CE level复形的类关于纯子复形和纯商复形封闭。
证明:由文献[6]可知level模的类关于直和、直积、直和项、正向极限、纯子复形和纯商复形封闭。再根据文献[5]可知结论显然成立。
推论1 设R是右凝聚环,则L是CE level复形当且仅当L是CE平坦复形。
证明:由文献[6]可知若R是右凝聚环,则M是level模当且仅当M是平坦模,所以结论显然成立。
命题3 设M是复形,则:
(1)M是CE绝对clean复形当且仅当M+是CE level复形;
(2)M是CE level复形当且仅当M+是CE绝对clean复形。
证明(1):由定理1可知M是CE绝对clean复形当且仅当…→P2→P1→P0→X→0和Pi属于C(A)。由文献[6]可知B-n-1(M)是绝对clean模,当且仅当(B-n-1(M))+是level模。再根据文献[4]可知Bn(M+)是level模,当且仅当(B-n-1(M))+是level模。同理,Hn(M+)是level模当且仅当(H-n(M))+是level模。由定理1可知M是CE绝对clean复形,当且仅当M+是CE level复形。
(2)同(1)。
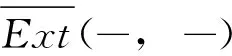
证明:由文献[6]可知(L,N)是完全余挠对。因为L是可解的,所以(L,N)是遗传余挠对。由文献[2]可知(CE(L)、CE(N))是遗传余挠对,再根据文献[4]可知(CE(L)、CE(N))是完全余挠对。
3 结 语
本文首先给出了CE超有限表示复形的充分必要条件是存在复形的CE正合列…→P2→P1→P0→X→0,其中Pi是CE有限生成投射复形。其次给出了CE绝对clean复形和CE level复形的等价刻画。接着给出了CE绝对clean复形的示性是CE level复形。最后给出了CE绝对clean复形和CE level复形关于直积、正向极限、纯子复形和纯商复形封闭的性质。
