六自由度压电隔振平台面向控制的模态分析与动力学建模

于帅彪，张臻，*，周克敏

（1.北京航空航天大学 自动化科学与电气工程学院，北京100083；2.山东科技大学 电气与自动化工程学院，青岛266590）

基于振动主动控制技术的六自由度压电隔振平台能够弥补被动隔振的固有缺陷，有效改进平台的低频隔振性能，提高隔振带宽。采用压电陶瓷、超磁致伸缩材料等智能材料的智能隔振平台提高了系统的控制精度和响应速度，在半导体制造、航空航天精密观测、瞄准等微振动控制领域得到广泛的应用［1-5］。

振动主动控制首先需要建立平台的动力学模型［6-7］。然而多自由度隔振平台各个控制通道间往往存在强耦合，同时压电陶瓷等智能材料固有的迟滞非线性特性会降低系统的控制精度甚至造成系统振荡，这都给平台系统的动力学建模与控制带来很大的挑战。独立模态空间法或模态分解法是基于模态分析技术［8］，利用模态坐标变换将系统解耦成一组独立的二阶系统（模态方程），根据每一阶模态独立进行控制器设计，获得模态坐标下的模态控制信号，再经过模态坐标反变换获得实际作动器的控制信号［9-10］。模态控制方案降低了多自由度耦合系统动力学建模与反馈控制系统设计的难度，在六自由度压电隔振平台控制中得到了应用［11-13］。已有的基于模态分析的多自由度平台动力学建模与控制工作中都未考虑压电等智能材料迟滞非线性特性对系统的影响。此外经典的模态分析技术通过实验测量或有限元方法获得结构的模态参数，但对模态控制信号物理实现过程中的转换关系研究很少。

本文针对一类模块化六自由度压电隔振平台，考虑压电材料迟滞非线性，基于模态分析方法建立面向控制的非线性动力学模型。模型采用Hammerstein结构描述平台非线性动力学特性，利用MPI（Modified Prandtl-Ishlinskii）迟滞模型描述非线性子系统［14］，利用模态分析技术将线性子系统变换为一系列独立的模态方程，采用实验测量方法辨识得到模态参数。同时还研究了模态控制信号到真实控制信号之间的转换矩阵，保证了模态控制的物理实现。

1 模块化六自由度压电隔振平台

六自由度压电隔振平台如图1所示。平台采用模块化的结构形式，其平面图如图2所示，每个隔振模块提供2个自由度方向的主动隔振能力，4个隔振模块与上下台面组合构成具有六自由度隔振能力的平台系统，G-XY为平面坐标系。

图1 六自由度压电隔振平台Fig.1 Six-degree-of-freedom piezoelectric vibration isolation platform

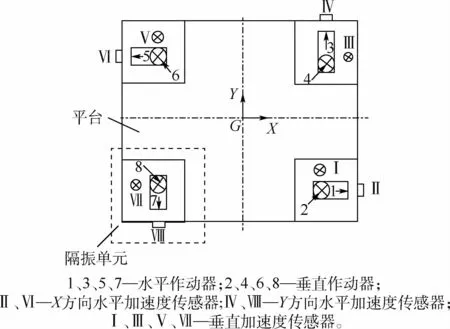
图2 六自由度压电隔振平台平面图Fig.2 Planar graph of six-degree-of-freedom piezoelectric vibration vibration isolation platform

1.1 两自由度隔振模块

两自由度隔振模块如图3所示，模块长150mm，宽160mm，高100mm。两自由度隔振模块采用主动隔振元件与被动支撑元件并联结构形式，在垂直和水平方向各布置一个压电作动器作为主动控制元件，垂直方向布置4个被动支撑组件作为主要的承重元件。考虑到微振动控制的高精度要求，主、被动元件与L型顶板之间采用专门设计的柔性铰链连接。

主动控制元件采用哈尔滨芯明天科技有限公司的VS系列压电作动器，标称推力为3 500 N，最大输出位移为40μm。压电作动器与顶板连接采用空间曲线切口式柔性铰链，如图4所示，其中xmax和xmin分别代表x方向的最大和最小的位移。通过对切口形状参数、曲线截断参数以及切口间距的优化设计，使柔性铰链具有高轴向刚度和低弯曲刚度。

被动支撑元件与顶板之间的柔性连接结构采用一体化设计的金属／橡胶复合结构形式，如图5所示。

图3 模块化隔振单元Fig.3 Modular vibration isolation unit

图4 作动器柔性铰链Fig.4 Actuator flexible hinge

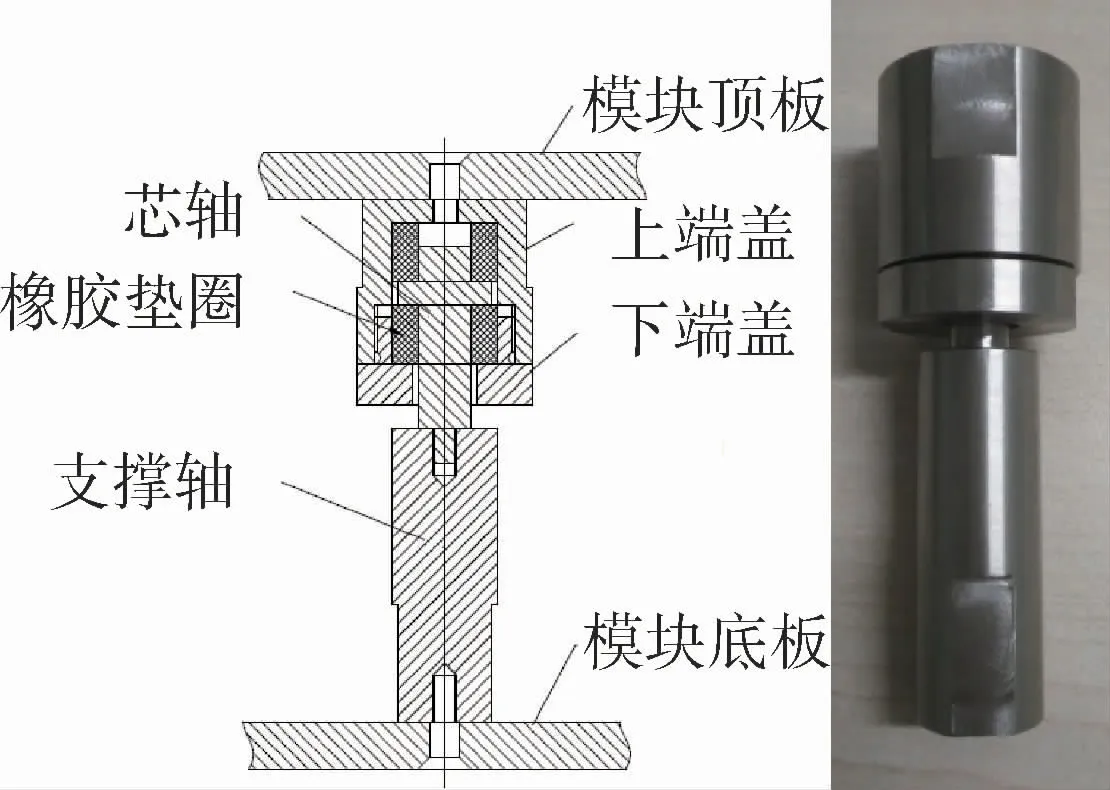
图5 被动支撑元件结构与实物图Fig.5 Passive support assembly structure and photo

1.2 六自由度压电隔振平台

六自由度压电隔振平台由4个两自由度的主动隔振模块和上下台面组成，结构如图1所示。隔振平台上台面为正方形硬铝合金，边长为500mm，厚度为20 mm。平台的8个作动器以及分别布置在水平以及垂直方向的8个直线加速度传感器如图2所示。

2 六自由度压电隔振平台模态分析与动力学建模

2.1 六自由度压电隔振平台模态分析原理

在本文中，上平台是系统控制和动力学建模的对象。考虑到上平台变形的影响，在m个主动驱动元件驱动下，由上平台l个测量节点表达的上平台运动方程可以写为

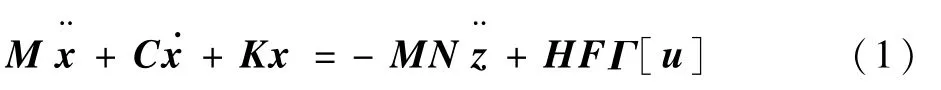
式中：x为l×1维的上平台相对运动向量；u为m×1维的主动控制量；M 为l×l维的质量矩阵；C为l×l维的阻尼矩阵；K为l×l维的刚度矩阵；z为6×1维的直接作用在上平台上包含了不同扰动源的等效干扰向量；N为l×6维的扰动分布矩阵；H为l×m维的刚度矩阵；F为m×m维的作动器位移矩阵；Γ［u］＝［Γ1［u1］ Γ2［u2］ …Γm［um］］T为m×1维的静态迟滞子系统，Γn［·］（n＝1，2，…，m）为对应于第n个作动器的静态迟滞子系统模型。

对于一个实际的物理结构，质量矩阵M 是一个对称正定矩阵，刚度矩阵K至少是一个半正定矩阵，假设阻尼矩阵C同时满足振型正交性，由此可以引入模态变换实现对角化，即

式中：Φ 为l×l维的模态矩阵；ε为l×1维的模态运动向量。将式（2）代入式（1），则可以得到模态坐标下l个解耦的动力学方程为

模态坐标下动力学方程（3）中需要辨识的参数包括M*、C*和K*。由式（2）可得到真实加速度信号与模态加速度信号之间转换关系为

由式（4）可得到真实控制信号与模态坐标下控制信号的关系：

压电作动器的动态迟滞非线性模型可以由Hammerstein模型描述，表达为一个静态迟滞非线性子系统和一个线性动态子系统的串联形式［14-15］，其中压电作动器机械结构的动力学被认为是其动态特征的主要来源。式（1）也被看成是输入端为迟滞非线性的多入多出的Hammerstein非线性动力学系统，如图6所示，其中Γ［·］为静态迟滞非线性子系统，y（t）＝Γ［u］为静态迟滞系统量。线性动态子系统H为多自由度耦合系统，是平台机械结构的动力学响应，包含了压电作动器机械结构动力学响应对系统的影响。通过式（2）的模态坐标可将系统变换成如图7所示的模型，其优点是：模态方程是一组独立的二阶系统，因而可以据此设计独立的模态控制器，降低了控制器设计难度。控制量再经过模态反变换得到实际控制量。图8给出了基于模态变换后等效模型的控制流程。需要注意的是，式（6）中的迟滞逆补偿器Γ-1［·］被串联在被控对象之前，消除压电作动器迟滞特性对系统的影响。

图6 隔振平台Hammerstein模型Fig.6 Hammerstein model of vibration isolation platform

图7 模态变换后的等效模型Fig.7 Equivalent model after modal transformation

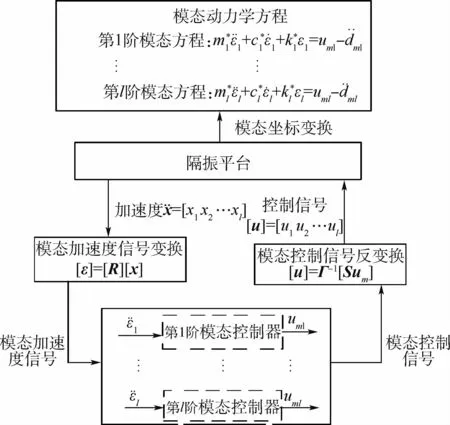
图8 模态控制流程Fig.8 Modal control process

在图7的等效模型中，需要辨识的参数包括模态振型Φ、质量M*、阻尼C*、刚度K*，转换矩阵R、S以及作动器静态迟滞非线性子系统模型Γ［·］及其逆模型Γ-1［·］。图中：y（t）＝Γ［u］为静态迟滞系统量；ξ（t）为模态控制信号，为输入，为经过模态方程变换之后的模态运动向量。

2.2 模态参数

本节采用Coinv DASP模态测试与动力学分析系统辨识系统的模态动力学参数。模态测试系统框图如图9所示，将平台上平面按照图10所示划分网格点，采用多点敲击单点响应，用力锤在2、12测点处沿X方向水平敲击，8、14测点处沿Y方向水平敲击，1、5、9、13测点处沿Z方向垂直敲击，加速度传感器的信号经由电荷放大器传送给DASP系统。模态拟合采用频域拟合方法。

本文上平台在结构设计中虽然尽量设计为刚性，但上平台的弹性变形仍不应完全忽略。为保证系统的可观测性，8个直线加速度传感器被布置在如图2所示的位置，其中垂直方向布置4个，2个水平方向各布置2个。

图9 模态测试系统框图Fig.9 Block diagram of modal test system

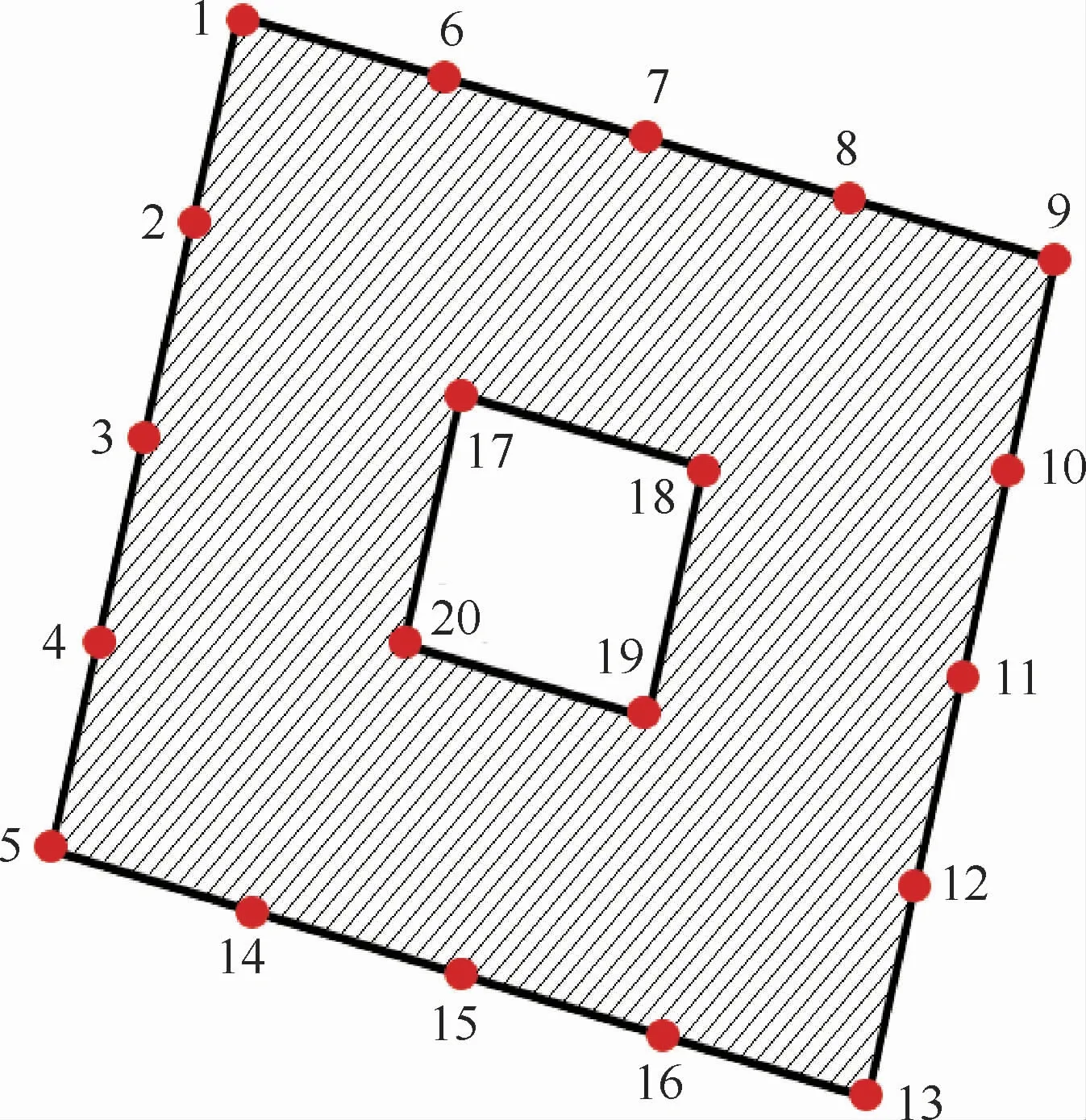
图10 隔振平台划分网格图Fig.10 Grid diagram of vibration isolation platform

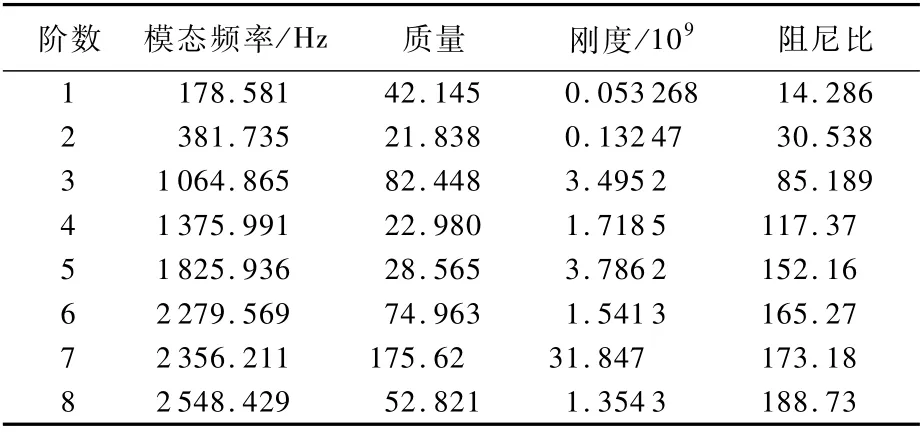
表1 模态频率、质量、刚度和阻尼比Table 1 Modal frequency，mass，stiffness and damping ratio

测得模态频率、质量、刚度、阻尼比如表1所示。振型矩阵在整个模态控制过程中需要用到2次，可见其结果的准确性对于控制过程的重要性。第1次是利用振型矩阵将平台的物理位移转换为模态位移，第2次是利用其进行真实控制信号与模态控制信号之间的转换。根据实验获得的模态分析测试结果，将每阶模态下平台振动的形态用模态振型Φ 并采用X、Y、Z轴进行直观的表示，如图11所示。其中第1阶模态以X向平动为主，其他各阶模态既有平动和转动的存在，也包含了可能存在的弹性变形。

2.3 迟滞非线性子系统建模

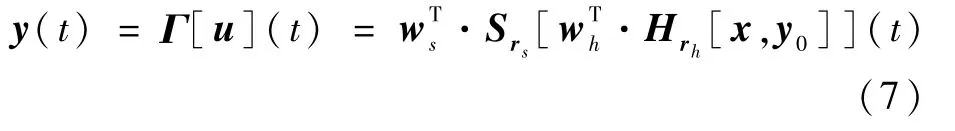
本节采用MPI算子建立静态迟滞非线性子系统模型Γ［·］，并给出了其逆补偿器Γ-1［·］。MPI算子可以写为式中：Hrh＝［Hrh0Hrh1… Hrhn］T，Hrhi为阈值为rhi的play算子；Srs＝［Srs0Srs1… Srsn］T，Srsi为阈值为rsi的死区算子；wh＝［wh0wh1… whn］T、rh＝［rh0rh1… rhn］T和y0＝［y01y02… y0n］T分别为play算子权值向量、阈值向量和play算子初始值向量；ws＝［ws0ws1… wsn］T和rs＝［rs0rs1… rsn］T分别为死区算子权值向量和阈值向量。

给压电作动器系统0.5 Hz低频正弦信号作为激励信号，基于输入输出数据采用最小二乘法辨识模型参数，具体辨识算法详见文献［16］。8个作动器按照相同的阶数进行建模，根据辨识算法得到1号作动器对应的静态迟滞非线性子系统相应的权值向量为

同理可得到其他作动器对应的静态迟滞子系统相应的权值向量。图12给出了1号作动器对应迟滞子系统建模结果，建模结果表明MPI算子可以准确地描述系统的迟滞特性。

图11 隔振平台振型辨识结果Fig.11 Vibration isolation platform vibration type identification results

表2给出了8个作动器对应静态迟滞子系统的建模误差，建模精度由均方根误差来评价，定义为

当MPI模型满足一定不等式约束条件时，式（7）表示的模型具有唯一的解析逆，其逆模型的表达式为［17］

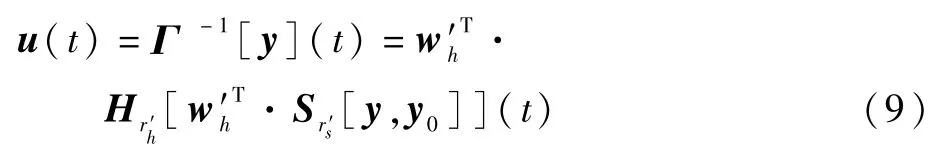
逆模型参数与式（7）中参数具有一一映射关系。图13给出了1号压电作动器迟滞逆补偿的实验结果，由图中可见，逆补偿器很好地消除了压电作动器的迟滞特性。8个作动器的逆补偿实验结果如表3所示。

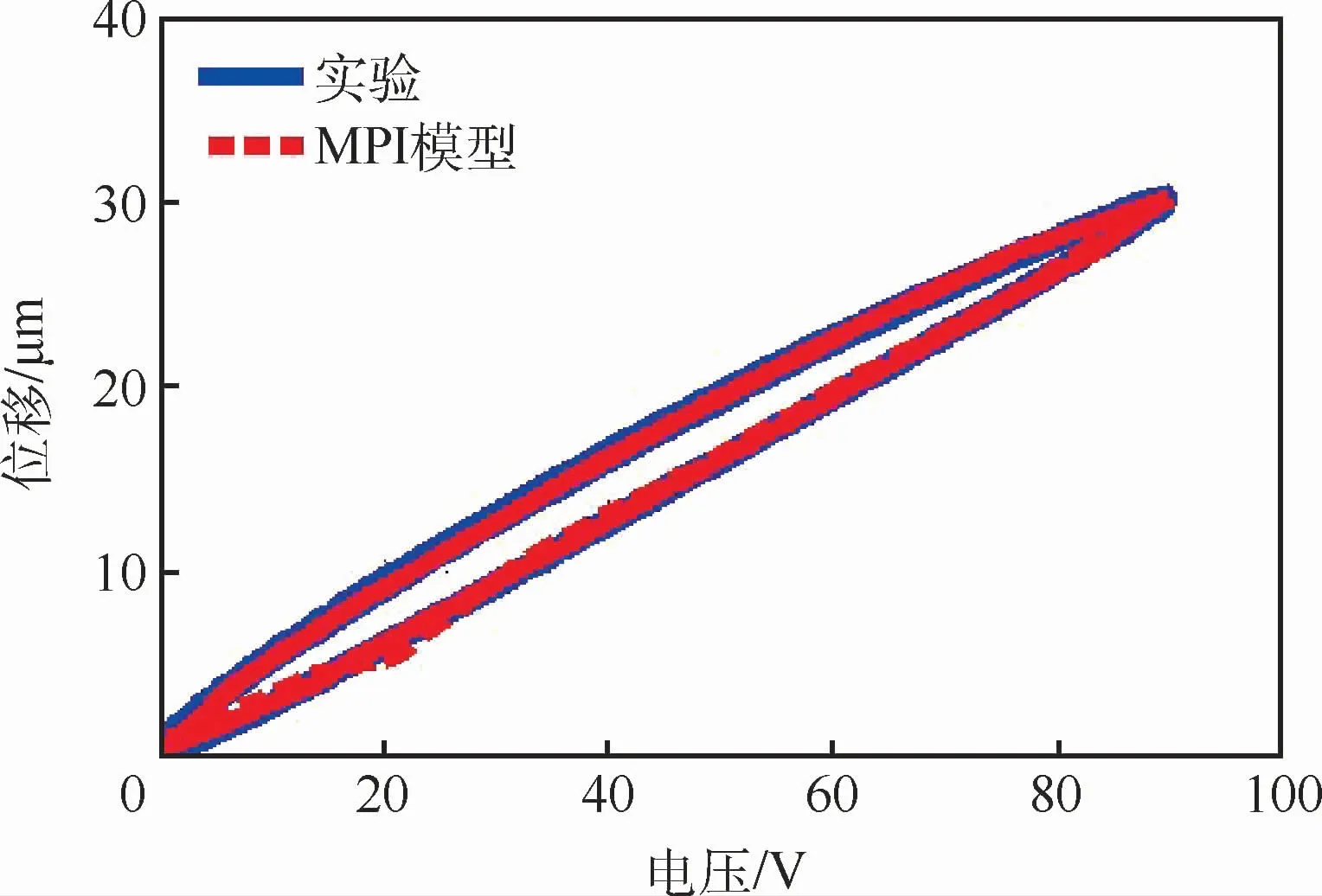
图12 压电作动器迟滞模型建模结果Fig.12 Hysteresis modeling results of piezoelectric actuator

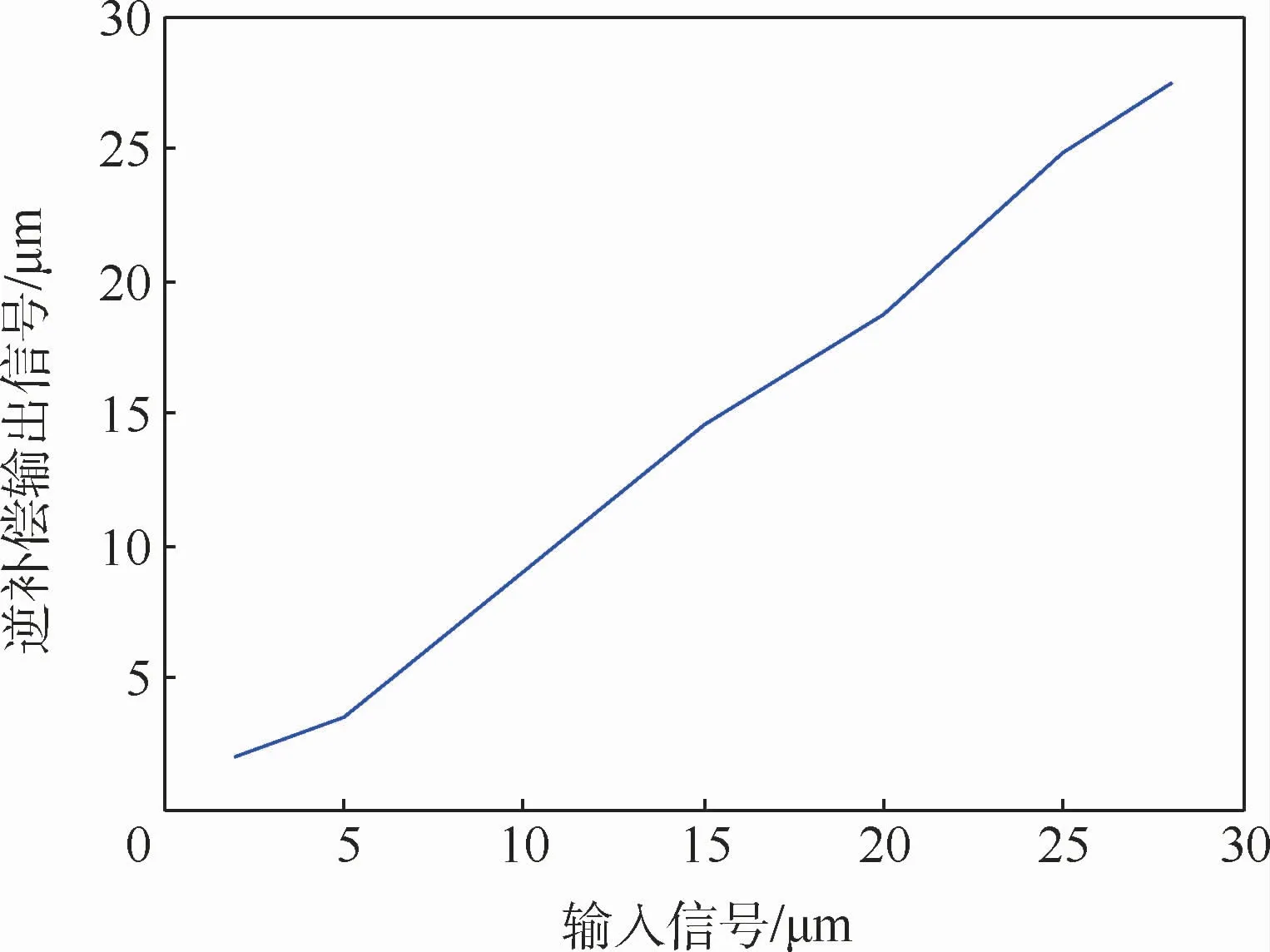
图13 逆补偿实验结果Fig.13 Inverse compensation experimental results

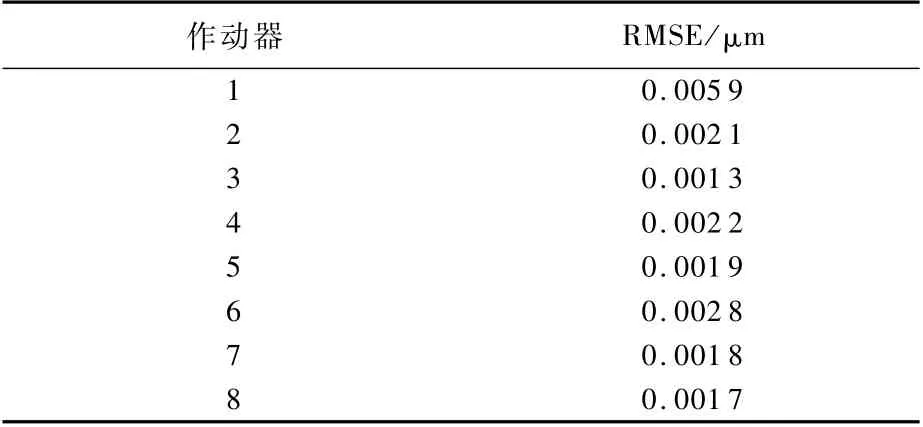
表2 M PI模型建模误差Table 2 Modeling error of MPI model

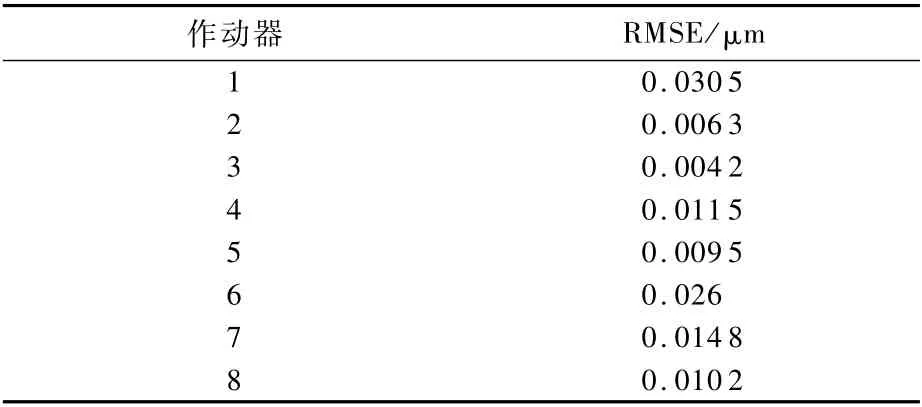
表3 逆补偿实验结果Table 3 Inverse compensation experimental results

2.4 转换矩阵辨识

1）R矩阵。基于2.2节得到的振型矩阵Φ，由式（5）可以得到R矩阵为

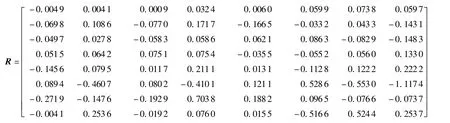
2）S矩阵。HF矩阵可以近似为平台在抵消了迟滞特性后各个输入／输出通道传递函数在低频阶段的增益，即各个通道的刚度。图14给出了辨识HF的框图，其中ui（t）表示作动器的电压输入，xi（t）表示8个测量节点的相对运动向量，各个通道迟滞逆补偿Γ-1［·］根据2.3节所辨识得到的各个通道的迟滞模型由式（9）计算得到。由式（6）最终可以得到S矩阵为

图14 HF辨识框图Fig.14 Block diagram for HF identification

3 结 论

本文针对六自由度压电智能隔振平台开展了面向控制的动力学建模研究，为了解决系统中存在的耦合问题，建立解耦后的模态方程，得出：

1）在考虑压电作动器迟滞特性的情况下，基于模态分析方法建立了平台的动力学模型，为后续的模态控制器设计提供解耦后的动力学方程，并为控制回路的物理实现提供信号在不同坐标下的转换关系。

2）采用MPI算子建立了系统的迟滞非线性模型，设计的逆补偿器通过实验验证有效地消除了迟滞非线性的影响。