中国林业全要素生产率及其收敛性分析

周 越，梁小珍

（上海大学 悉尼工商学院，上海201800）

林业全要素生产率（total factor productivity，TFP）指林业产出中由除以劳动力和资本为代表的全部生产要素投入量以外的因素来解释的部分，从而度量不同地区和国家的林业生产率水平。如何科学准确的测算林业全要素生产率，是进一步分析林业发展方式由依靠资本、劳动力等投入要素的增加，进一步转变到提高林业生产要素的使用效率上来，从而提高在所研究区域的林业经济增长中的贡献份额[1-2]。从现有的实证研究方法来看，对林业生产效率的测算和分析研究主要数据包络分析法（Data Envelopment Analysis，DEA）和随机前沿分析（Stochastic Frontier Analysis，简称SFA）。此外部分研究文献也采用了其他一些实证研究方法如：生产函数法、索罗余值，成本收益分析法和增长核算指数法等[3]。国内外学者基于这些不同的研究方法，研究了全球不同区域的林业全要素生产率及其各区域的林业发展效率特征、趋势和路径[4-8]。

国内外早期的针对林业生产效率研究以理论分析为主，而基于数据的实证研究相对较少，其中只有少数学者对全要素率进行测算。之后的国内外基于定量研究方法的林业全要素生产率的研究开始逐渐发展，主要研究了不同地理纬度上的区域、国家林业全要素生产率变动情况或针对某一具体林业分行业的全要素生产率变动情况进行研究和分析[9-10]。从针对我国林业的全要素生产率的研究文献来看，近年来许多研究文献开始采用DEA 等方法对我国林业效率问题进行实证研究，从而科学的核算和分析我国不同地区的林业生产效率及其区域差异性。如黄安胜（2015）等结合DEA 方法测算了包含较多投入、产出指标的多重目标下林业全要素生产率及时空差异，但没有考虑投入产出的时滞性和生产率的收敛性。其次，基于全国31 个省份林业相关截面数据，运用DEA方法，丁胜等（2019）测算了2016 年全国林业的规模效率，核算平均值为0.588，核算结果表明我国规模经济效率不高，且由于资源浪费等原因而导致我国林业发展的规模不经济。

在对全要素生产率进行定量研究中，另一个重要的方面是进行相应的收敛性分析，从而反映区域差异的变化动态情况，常用于研究区域经济发展之间的差距变动。从现有的研究文献综述来看，具体收敛性分析用于全要素生产率差距分析的主要有σ 收敛、绝对β 收敛、条件β 收敛。如：在测算和分析1982—2002 年各省区全要素生产率的基础上，彭国华（2005）介绍了绝对β 收敛的理论，进行了全要素生产率的收敛检验，并与人均收入的收敛模式进行了对比分析[16]；李谷成（2009）测量了农业TFP增长的地区差异并进行绝对β收敛性分析。基于1993—2010年的中国29个省份的面板数据，采用Malmquist-Luenberger 生产率指数方法，韩海彬和赵丽芬（2013）分析研究了环境约束下我国29 个省份的农业全要素生产率增长及其进一步的收敛性检验和分析研究[17]；基于所构建的DEA-Malmquist指数法模型，姜钰和管时一（2017）在测算林业全要素生产率的基础上对其进行了不同时间维度上的收敛性分析，他们的实证研究结果将其收敛性分成了三个阶段，并分析了不同发展阶段的变化特征[18]，表明只有2008-2011是发散期，其他时期都存在显著收敛。

本文基于DEA 测度的非参数方法，进一步将DEA 和Malmquist 指数法的理论相结合，构建了DEA-Malmquist指数的实证模型，测算并分析了我国林业的全要素生产率。

1 数据来源与指标选取

1.1 投入产出指标

指标选取上要同时考虑指标的质量和数量，以全面的反应林业生产的投入和产出。基于现有研究，本文基于对林业生产有较大影响的3个方面进行指标选取，包括投入产出指标相关程度、投入产出指标数目和多项产出决策单元（Decision-MakerUnit，简称DMU）样本评价单元的规模3 个方面。特别注意，样本评价单元规模大于或等于投入产出指标数之和的三倍。目前引用率较高的文献选取指标情况如表1所示。

表1 相关指标汇总

土地投入、劳动投入、社会产出类指标选取比较统一，资本投入、经济产出类指标选取存在一定的分歧，生态产出类指标大部分选择用森林储蓄量来表示，少部分文献选择了新增造林面积。

基于数据的可得性和研究结果的合理性，本文选取了中国大陆31 个省份2006—2015 年间的林业生产面板数据，模型构建采用一投入多产出为主，多投入多产出为比较方案的办法。

在林业投入变量中，劳动投入变量以林业系统各部门从业人员年末总人数来计算作为代理指标；三个资本投入变量代理指标，基于我们的实证研究，采用了实际到位资金（万元）作为模型的资本投入指标；考虑到中国林业用地面积每5年统计一次，面板数据模型中的土地投入代理指标，我们对该变量每5年采用相同的统计值。

关于林业产出代理变量中经济产出代理变量，本文选择了中国林业产业总产值。以总产出作为产出指标，能够更为合理的反映中国林业整体资源配置的改善和规模节约效能，这与TFP 关于产出的定义更为一致。在该指标的数据处理中，考虑到消除价格因素影响，基于各省份的消费价格指数，将以当年价格测算的中国林业产出总产值换算为以2006年不变价格测算的产值。

1.2 数据描述

本文选取了2006—2015 年间我国31 个省份的面板数据作为我国林业生产率的研究样本，其中31 个省份具体包括11 个东部省份、8 个中部省份和12 个西部省份，文中投入产出指标的主要数据来源于中国历年的《中国统计年鉴》和《中国林业统计年鉴》。从2006年不变价的林业总产值指标来看，我国林业在2006—2015 年期间呈现出持续增长的态势，林业总产值从2006 年的336.28 万元逐年增长到2015年的5.936 3亿元。

投入变量中，从业人数在所研究的样本区间总体呈现出波动下降的态势。从平均增长率来看，中国林业产业从业人员以年均18.3%的速度下降，且从2010 年开始呈现出逐年连续下降的态势，截至2015 年林业从业人员下降至样本期间的最低点120.43万人。以2006年为例，从业人员的区域分布具体为：11 个东部省份从业人员占比为15.91%；12个西部省份从业人员占比为34.1%；其余8个中部省份从业人员占比为49.99%。而实际完成的投资额上升到研究区间的最后一年出现回落。每年完成投资情况从2006年的631.027亿元增长到了2015年的4 290.142亿元（折算后），平均每年增长23.7%。

2 中国林业全要素生产率的时空差异实证分析

2.1 2006—2015年林业全要素生产率的总体趋势

基于时间发展上分析的整体趋势来看，如表2 和图1 所示，在样本期2006—2015 年，实证结果表明中国林业全要素生产率（tfpch）基本实现平稳增长，年均增长率为6.1%，部分分效率指标相对较差，如林业技术效率增进指数年均增长0.1%，而规模效率指数年均降低2.4%。具体分析来看，前几年（2006—2009）人员、资金投入的贡献增多，全要素增长率只有-2.4%，后面全要素生产率开始增长，即人员、资金的贡献降低，用技术进步等其他要素解释的贡献平均上升10.69%。其次，实证研究结果发现，技术效率变化（effch）与技术进步指数（techch）在多数时期呈现出相反的发展特征（计算结果符合effch*techch 约等于tfpch 的前提，即假设全要素生产率受两个指标共同影响）。研究结果还表明，我国农业全要素生产率指数变化趋势与技术效率增进指数、技术进步指数趋势变化基本实现一致，在2008—2012 年与技术效率变化更为接近，而在2012—2015 年受技术效率增进指数影响更多；而规模效益贡献是负值，表明中国林业整体发展还没有达到预期规模效益。

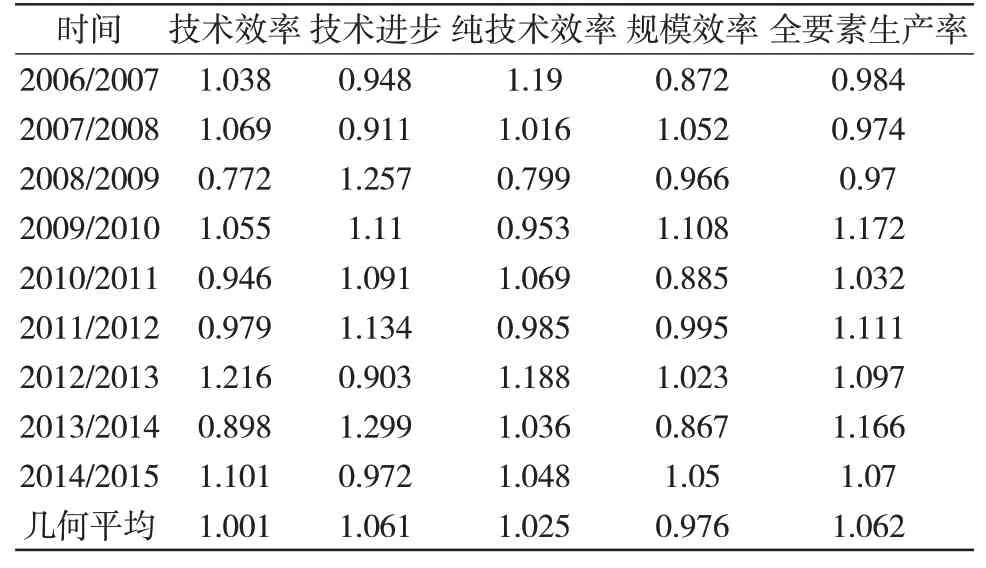
表2 中国林业全要素生产率（年度平均）指数及其构成的变化

2.2 林业全要素生产率区域比较分析

从区域全要素生产率来看，除了海南、西藏、内蒙古、吉林、黑龙江区域以外，其他省份10 年间全要素生产率增长率都大于1，表明大部分区域全要素生产率都是增长的。这几个省份的特点是森林储蓄量远大于其他省份。

将我国林业区域划分为东部、中部、西部三大区域来分析，东部地区发展以平原林业为主，即农田、沟渠等地的防护林；中部地区属于林业发展的优势地区，人工林占比大；而西部地区则多为生态脆弱地区，是生态恢复区与建设区域。从三大不同区域的时间趋势发展比较来看，在前几年（2006—2011）东部省份全要素增长率整体大于中西部省份，到了后半段（2011—2015）东部省份增长速度落后于中西部，如表3所示。

2.3 收敛性分析

σ 收敛性的图形可以用变异系数来显示。取每年中国林业不同区域的曼奎斯特指数平均数和标准差，得到变异系数（C.V.）。变异系数除了2008 年由明显的增长并紧接着出现回落以外，大体呈降低趋势。这与2008 年全球金融危机造成的经济不稳定性有一定关联。σ 收敛性分析的模型如下：

FTFPi,t代表在t时期第i个区域的林业全要素生产率，代表全要素生产率平均数。从图2 所示的中国林业全要素增长率的σ 收敛情况来看，中国的林业经济大致分可以为3个阶段：分别为2006—2008 年不太显著的σ 收敛阶段、2008—2010 年的发散阶段、和2010—2015 年处于比较显著的σ收敛阶段。根据σ收敛性图形的变化特点，选择T=3，得出一组滞后变量，对正常变量与滞后变量分别取对数，然后得出对数之差。最后对等式左边公式得到的数组和等式右边的数组进行多元回归，求得β 值。此处只求得α和ε之和，不需要求得α和β的具体值。

图1 中国林业全要素生产率指数及其分解变化趋势

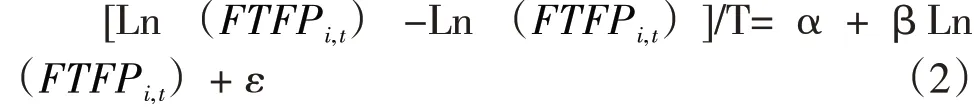
β=-0.004 891 ＜0（Pr（＞|t|） =0.755，β＜0，所以存在绝对β收敛。

选择T=1，得出一组滞后变量，对正常变量与滞后变量分别取对数，然后得出对数之差。最后对等式左边公式得到的数组和等式右边的数组同样地进行多元回归，求得β 值。此处也不需要求得α和β的具体值。

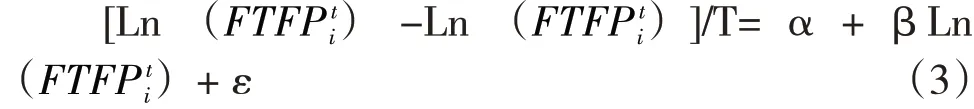
得到β=-0.005 954＜0，Pr（＞|t|）=0.475，同理存在条件β收敛性。

3 结论和政策建议

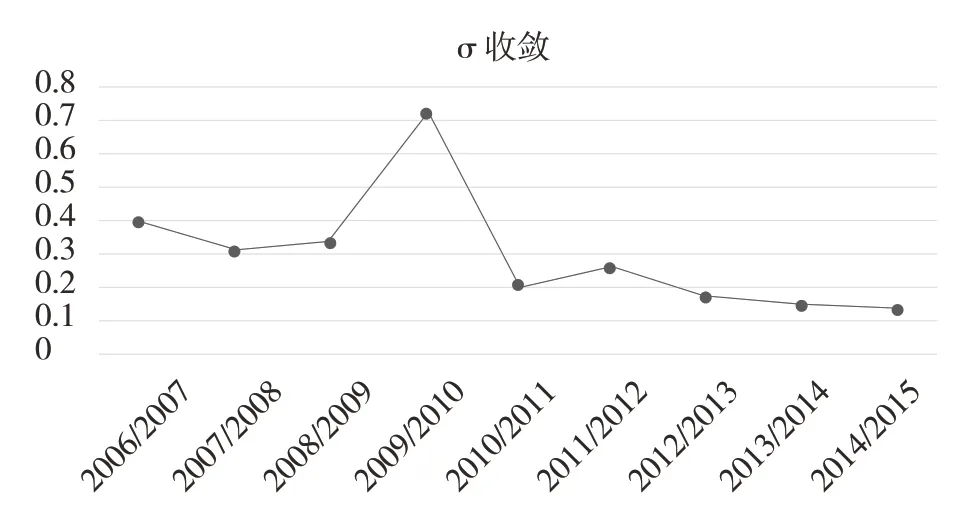
图2 中国林业全要素增长率的σ收敛情况

本文基于2006—2015 年31 个不同省份投入和产出的面板数据，运用DEA的非参数Malmquist指数方法，测算和分析了中国林业全要素生产率在时间维度上的发展特征和空间维度上的差异性，并进行了相应的收敛性检验，且进一步将全要素生产率分解为纯技术效率、规模效率与技术进步上分效率指标进行了不同效率的分析。整体来看，中国林业全要素生产率增长较快，年均增长速度为6.1%；其中技术效率对全要素生产率的影响相对较大。因此，除了技术的引进或创新之外，还必须进行适当的管理创新及制度变化。纵向来看，我国林业TFP 增长存在小幅波动，分为2006—2009 和2009—2015 两个阶段，两段平均全要素增长率分别为-2.4%和10.69%。这说明林业生产率增长易受到宏观经济环境的影响。

从区域来看，西部地区林业TFP 增长率为10.4%，中部省份林业TFP 增长率为6.39%，东部地区TFP 增长率为13.45%，区域间差异较大，即东部和西部TFP 增长率远大于中部区域。西部区域近年来发展加快，基础设施建设等投入和自身资源的合理利用带动了当地的经济发展。在后续发展中可以利用基础建设的优势适当增加旅游开发，但也要同时注意环境保护。针对我国东部经济发达地区而言，林业经营的机会成本较高，但同时全要素生产率增长较快。对于这部分区域，针对林业的专项补贴也是有必要的。

从各个省份单独看，中国各区域林业全要素生产率之间存在一定的差异。林业全要素生产率出现下降的只有个别省份，其特点是森林资源较丰富，但是经济发展速度不是特别靠前。充分了解这些区域林业发展效率的差异，可为我国的总体林业发展政策的制定提供科学的依据，并根据各区域林业自身发展的不同特点，制定相应的区域林业发展的制度。例如全要素生产率较高的东部省份面临同样的人口多、土地资源比较珍贵的情况，国家可以针对相似省份作出统一的战略部署，例如鼓励形成林业经济带。对于地理位置、资源和科技水平相似，但全要素生产率存在很大差异的地区，例如天津和北京等区域，可以就林业发展开展经验交流，从而带动低林业全要素生产率区域的林业发展。对于森林储蓄量占优的地区，可以加强森林资源的管理，对大量的从业人员加强培训，保障林农的利益，预防森林火灾等状况对林业经济造成巨大创伤。对于经济欠发达地区的林业发展还需要政府的财政支持。

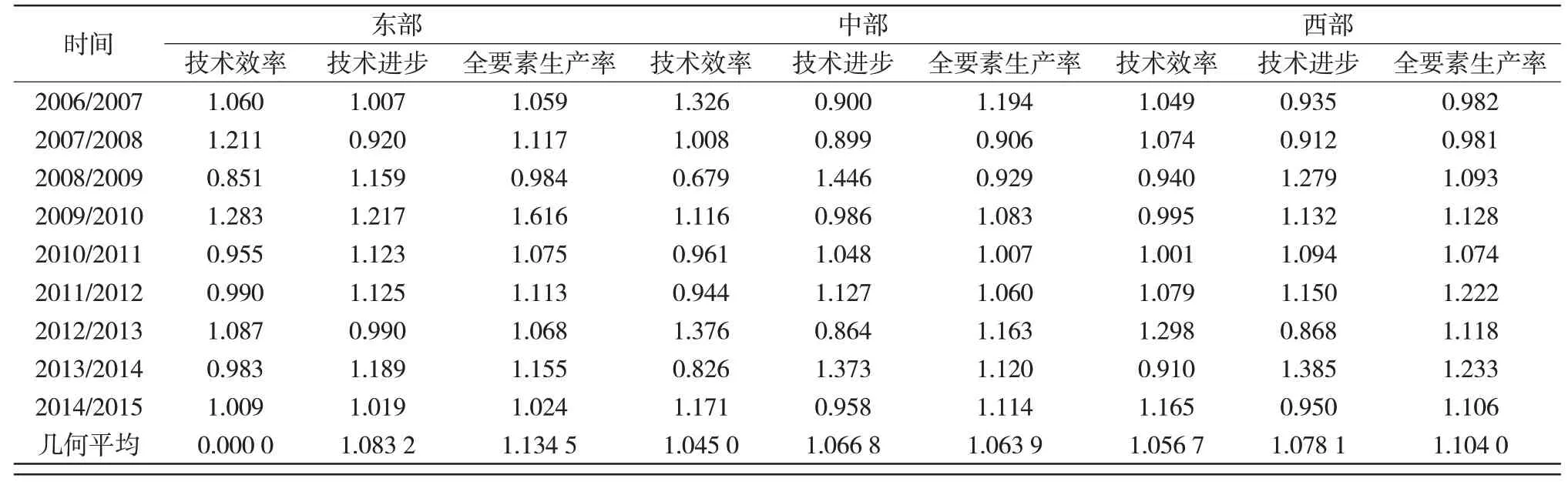
表3 中国三大区域林业全要素生产率及其构成变化

从中国林业全要素增长率的σ 收敛实证结果来看，中国的林业经济大致分可以为3个阶段：分别为2006—2008 年不太显著的σ 收敛阶段、2008—2010 年的发散阶段、和2010—2015 年处于比较显著的σ 收敛阶段。β 收敛检验结果表明，我国林业TFP 同时存在绝对β 收敛及条件β 收敛，说明林业TFP 在区域间保持了均衡。区域间全要素生产率差异受到经济环境的影响比较大，突发的经济金融事件和相应的政策应对措施会导致经济的稳定性受到破坏。然而，在2008—2009 年的金融危机事件伴随着经济周期的波动，相对在短时间内发生概率比较低。因此国家在制定经济政策时应考虑到给产业带来的区域发展差异。