基于等效结构应力法的焊接构架疲劳损伤评估

杨广雪, 刘志明, 李广全，董 磊

(1. 北京交通大学 机械电子控制与工程学院, 北京 100044； 2. 中车青岛四方机车车辆股份有限公司，山东 青岛 266111；3. 中车长春轨道客车股份有限公司 转向架开发部, 吉林 长春 130062)

转向架构架是轨道车辆主要组成部分之一，是安装各种零部件的载体，承受和传递由车体产生的垂向、纵向、扭转载荷等。随着列车速度的不断提高，线路激扰频率范围加宽，而转向架构架自重的减轻，降低了其固有频率，这样就导致构架的低阶弹性模态可能处于线路的激扰范围之内，从而使构架的某些部位产生较大的动态变形[1-2]。

某型焊接构架使用至今已有20余年，近年来在运用中多次出现疲劳裂纹，其发生部位均在构架横梁和侧梁连接区的焊缝部位，见图1。构架关键部位出现疲劳裂纹极大地威胁着列车的运营安全，因此，分析焊接构架疲劳开裂原因及关键焊缝部位的疲劳强度对防止事故发生、设计新型结构、保障我国铁路客运安全性具有重要的工程意义。

构件发生断裂主要是由于裂纹的存在，而裂纹萌生并扩展到足以引起断裂的原因大部分是由疲劳引起的[3]，对于焊接结构，疲劳裂纹源一般发生在焊接接头的焊趾区。目前，焊接结构的疲劳强度分析主要依赖于众多工业领域及国内外的一些标准所推荐的名义应力法，通过与相应的不同等级焊接接头S-N曲线相结合的方式来计算焊接构件的疲劳损伤。例如，英国BS 7608—1993[4]提供了大量的焊接工艺建议和更为丰富的钢结构和铝合金焊接接头抗疲劳设计数据。然而在实际工程应用中存在以下2个主要问题[5]：第一，由于焊接接头几何不连续性，很难从有限元模型中获取名义应力和接头处的弹性应力集中系数；第二，由于焊缝等级评定不仅与接头几何形状有关，还与焊接件所受的载荷模式有关，因此在选用焊接接头S-N曲线计算疲劳损伤时具有一定的主观性。

为更好地对焊接构件进行疲劳强度分析，在20世纪90年代提出了热点应力法[6]，该方法利用线性外推的方式求解接头焊趾处的热点应力值，但在有限元分析中，外推点的选择、单元类型及网格大小等对分析结果具有一定的影响。董平沙[5]提出了一种基于断裂力学理论及大量疲劳试验的新型焊接结构疲劳分析方法——等效结构应力法，该方法已被纳入美国ASME标准中。实践表明，该方法可比较准确地计算出空间任意走向焊缝的疲劳寿命[6-8]。

本文针对该焊接构架出现疲劳裂纹问题展开研究，建立了包含焊缝轮廓在内的焊接构架有限元模型，利用等效应力法对关键焊缝进行疲劳损伤计算，并与线路试验进行了对比分析，研究结果可为制定符合我国线路条件的设计规范提供一定参考。

1 等效结构应力法原理

1.1 基本理论

等效结构应力法以垂直于焊缝方向的结构应力为控制参量，对各种类型焊接结构进行疲劳强度分析。该方法应用于板壳有限元模型时主要考虑了以下3个方面：(1)在结构设计阶段一般不考虑拐角处焊缝的影响，而应用等效结构应力法对板壳有限元模型进行应力分析时应建立焊缝轮廓[6]；(2)焊趾缺口处应力的奇异性导致结构局部应力对网格尺寸具有一定的敏感度，采用等效结构应力法可有效消除或缓解网格尺寸、单元类型等对计算结果的影响，从而有效区分不同接头类型焊趾应力集中情况；(3)以结构应力作为控制参量计算应力强度因子，基于Paris裂纹扩展理论与大量试验数据分析确定与疲劳寿命相关的参数，构建出以等效结构应力为控制参数的疲劳设计主S-N曲线，对焊接构件进行疲劳强度分析及寿命预测[7]。

1.1.1 结构应力的数值计算

在实际焊接构件中，焊趾缺口处应力分布状态通常是非线性的，而结构应力定义中不考虑非线性应力的影响，其值为膜正应力和弯曲正应力之和

σs=σm+σb

( 1 )

式中：σs、σm、σb分别为主板表面结构应力、沿主板厚度t分布的膜正应力、弯曲正应力。

等效结构应力法应用于板壳有限元模型时，单个单元的受力状态见图2。假定单元节点1到节点2之间的直线(距离为l)为焊线，则由单元受力状态建立力平衡和弯矩平衡方程

( 2 )

式中:Fyi为第i个节点在y向节点力；x为焊线方向的距离；fy(x)为单元焊线的y向线力密度函数；xi为第i个节点距坐标原点的长度；l为单元节点1到节点2间的直线长度。

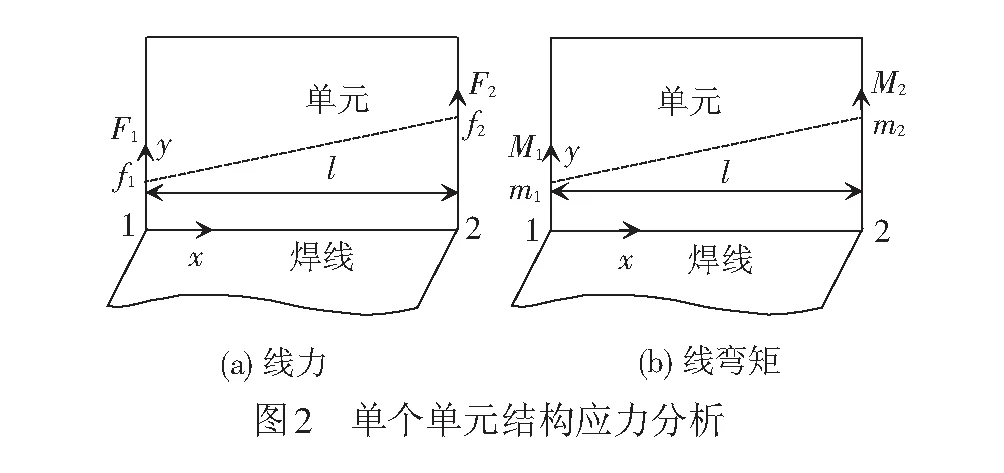
根据式( 2 )，得到节点处线力

( 3 )

式中：fy1、fy2分别为节点1、2处的线力值；Fy1、Fy2分别为节点1、2处的节点力。

同理可得到节点弯矩为

( 4 )

式中：mx1、my2分别为节点1、2处的线弯矩；Mx1、Mx2分别为节点1、2处的弯矩。

根据结构力学理论，可计算得到每个节点垂直于焊缝方向的结构应力为

( 5 )

式中：t为结构板厚；fy为节点线力值；mx为节点线弯矩。

有限元模型进行受力分析后，可获取垂直于焊线的单元节点力F和节点弯矩M，然后根据式( 2 )—式( 5 )确定垂直于焊线的结构应力。

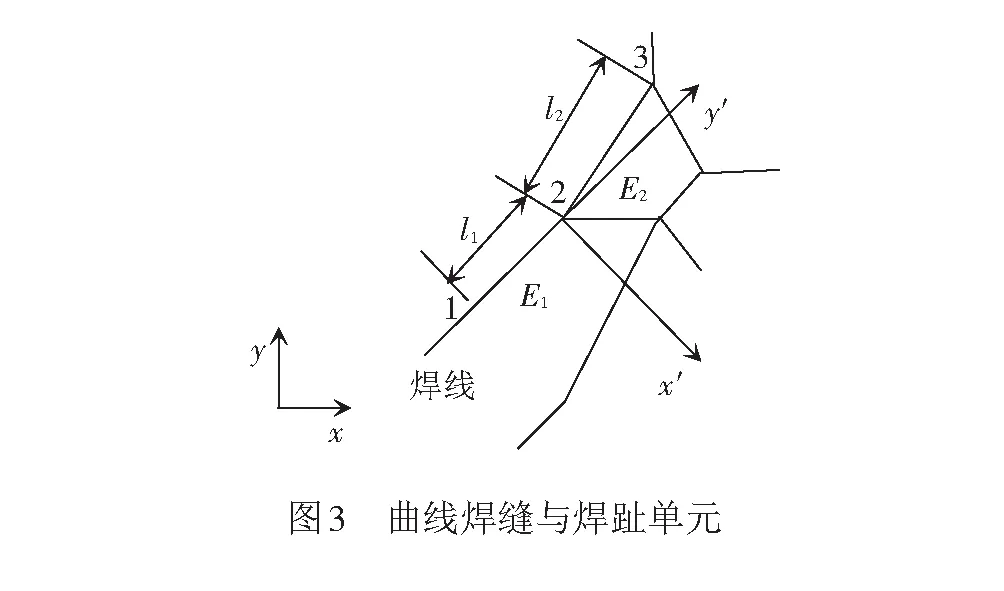
在实际焊接结构建模时，焊线是由多个单元边组成的一条直线或曲线，见图3，E1、E2分别为单元1、单元2。在这种情况下，应考虑整个焊线上单元节点的力平衡和弯曲平衡条件，计算结构应力所需的线力和线力矩可按功等效原理建立联合方程组，求解线力公式为

( 6 )

式中：F1，F2，…,Fn为局部坐标系中x′方向焊线上的单元节点力；l1,l2,…,ln-1为局部坐标系下焊趾单元沿焊线的边长；f1,f2,…,fn-1为局部坐标系下焊线上的单元节点线力，同理可得求解单元节点线力矩的联合方程组。

1.1.2 疲劳设计主S-N曲线的确定

疲劳裂纹扩展划分为2个阶段：短裂纹阶段(a/t≤0.1)和长裂纹阶段(a/t>0.1)，基于Paris裂纹扩展理论的裂纹扩展模型为

( 7 )

式中：a为裂纹扩展深度；N为预测疲劳寿命值；Mkn为焊趾缺口导致的应力强度因子放大系数，用于短裂纹时需进行修正；n为短裂纹扩展阶段的裂纹扩展指数，按照经验取值为2；h为常规的Paris方程裂纹扩展指数，取值为3.6；C为材料的裂纹扩展参数；ΔKn为板边缘裂纹尖端的应力强度因子，其值可通过公式获取

ΔKn=

( 8 )

其中，fm(a/t)和fb(a/t)分别为膜正应力和弯曲正应力单独作用时确定应力强度因子范围的无量纲权函数

( 9 )

(10)

由此可得预测疲劳寿命应用的裂纹扩展方程为

(11)

式中：I(r)为载荷弯曲比r(r=Δσb/Δσs)的无量纲函数，为载荷模式的修正系数。在焊接结构中，对于半椭圆型裂纹扩张

I(r)1/h=2.154 9r6-5.042 2r5+4.800 2r4-

2.069 4r3+0.561r2+0.009 7r+1.542 6

(12)

从而构建出等效结构应力

(13)

式中:S、Δσs为焊缝焊趾处的等效结构应力值、结构应力范围。

文献[8]根据大量焊接接头及不同载荷模式下的疲劳试验数据确定基于等效结构应力的疲劳设计主S-N曲线方程

Sm·N=C0

(14)

式中：m为疲劳设计主S-N曲线斜率正值；N为等效结构应力值对应的循环次数；C0为焊接结构材料参数。

1.2 方法验证

1.2.1 网格尺寸不敏感性分析

在有限元建模分析中，焊趾处单元尺寸及单元类型对分析结果具有一定的影响。为考察焊趾处单元大小对等效结构应力法的影响，从文献[9]中选取2组对比数据，该数据包含试验法、热点应力法及结构应力法所获取的结构应力集中系数KS，其中有限元模型采用不同尺寸网格进行划分，计算结果见表1。

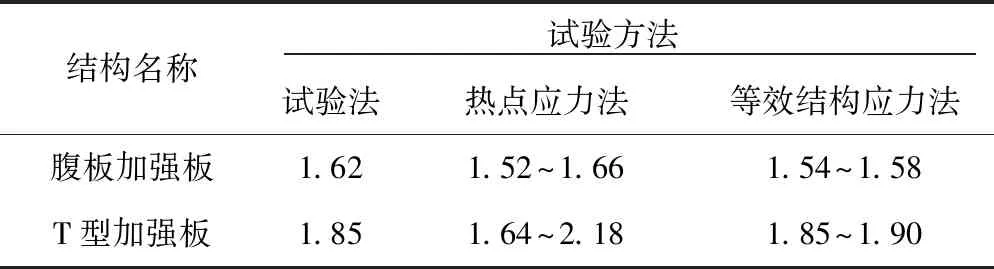
表1 结构应力集中系数KS

由表1可以看出，利用等效结构应力法计算出的应力集中系数离散度较小，与试验法的获取值近似相等，验证了网格单元大小对等效结构应力法具有不敏感的特性。同时，文献[10-11]通过对不同种类焊接接头在不同的载荷模式下进行应力分析，分析结果也表明等效结构应力法具有网格不敏感性。

1.2.2 试验验证

为验证等效应力法对焊接结构疲劳寿命评估的有效性，文献[12]采用材料为Q345E的焊接试件进行疲劳试验，疲劳试件的仿真分析结果和试验结果见图4。由图4可知，随着焊缝咬边深度的增加，试件疲劳寿命不断减低；仿真结果与试验结果较为接近，满足工程误差的要求。

文献[13-15]对T型焊接接头进行了疲劳分析，其分析结果见表2。由表2可知，等效结构应力法的计算结果与试验值最为接近，与热点应力法相比，等效结构应力法具有较高的计算精度。通过对T型焊缝和对接焊缝的疲劳分析可知，在焊接结构的疲劳损伤评估时，等效结构应力法具有较高的可靠性和适用性。

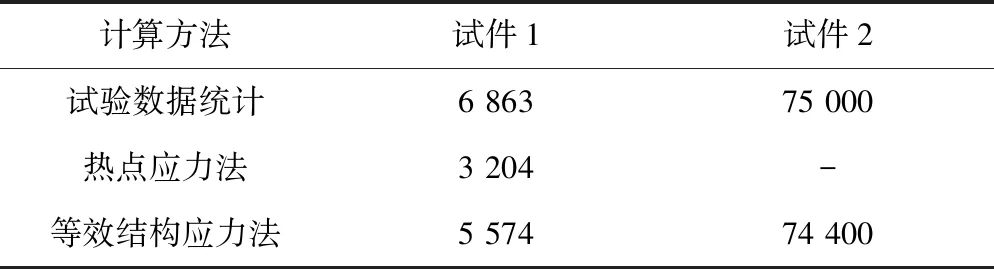
表2 疲劳寿命 次

2 焊接构架的疲劳损伤评估

2.1 有限元模型及载荷条件

该型转向架构架为H型形全钢焊接结构，由两侧梁和两横梁组成。侧梁由钢板焊接组成箱形封闭断面，内有筋板,横梁上焊有制动吊座等结构。该焊接构架在运用检查时发现横梁和侧梁连接处有裂纹出现。针对该现象，对横梁和侧梁连接处的3条主要焊缝进行疲劳强度评估，为更好地模拟构架关键部位的受力状态，有限元建模时考虑焊缝轮廓。

综合考虑整个构架的计算量、计算精度及构架的实际结构特点，选用4节点单元Shell181对构架进行离散，其有限元模型见图5。

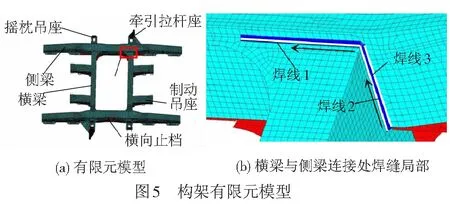
构架的主要载荷工况及受力位置见表3，设定载荷作用频次均为2×106。

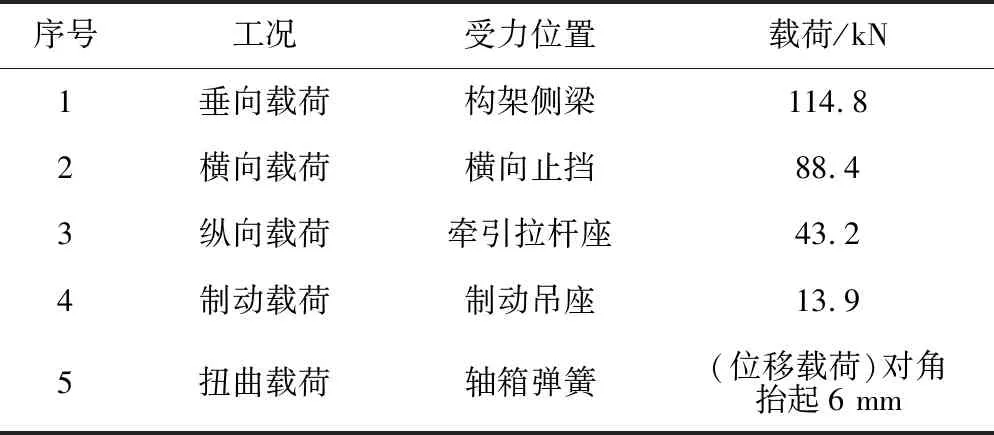
表3 构架模拟运营载荷

2.2 应力计算结果

对有限元模型进行结果分析，提取组合工况下局部坐标系中焊线上单元节点力和节点力矩，计算整条焊缝上的结构应力，从焊线起点到焊线终点的展开方向节点数为横坐标(节点沿图5 (b)中箭头进行编号)，与焊线上节点位置对应的应力幅值为纵坐标，计算结果见图6。

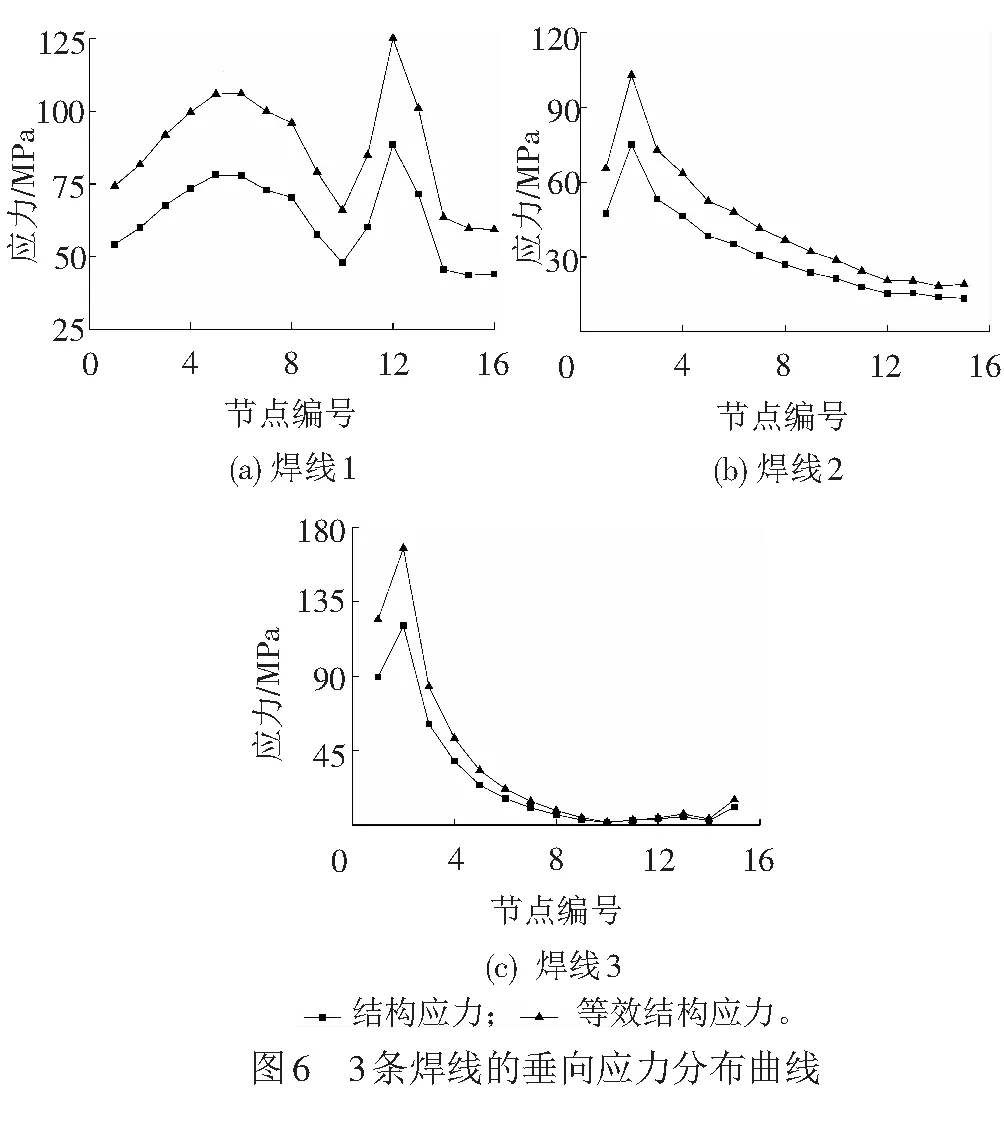
由图6可知，在焊线1焊缝中，节点5、6、12附近的等效结构应力幅值较大，最大值发生在节点12处，其值为125.1 MPa；在焊线2、3焊缝中，等效结构应力最大值发生在节点2附近，其值分别为103.0、167.4 MPa。在3条焊缝的结构应力分析中，焊线1焊缝节点5位于侧梁内部垂向隔板与侧梁纵向立板连接处，节点12位于横梁立板与横梁上盖板连接处；焊线2、3焊缝中的结构应力峰值发生在焊缝端部，此处为侧梁下盖板与横梁立板连接处，这些位置会使构架焊缝连接刚度不协调，从而易引起结构的应力集中。

2.3 疲劳累积损伤计算

根据Miner线性累积损伤理论和疲劳设计主S-N曲线可知，焊接结构的疲劳损伤D为

(15)

式中：N0为应力循环次数，对于焊接构件，N0取值为2×106。

根据式(15)和图6中的等效结构应力值，计算得到3条焊缝各节点的疲劳累积损伤值，见图7。

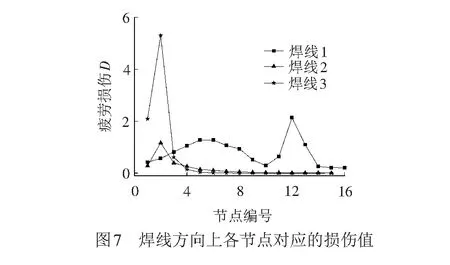
在实际应用中，必须考虑结构的安全裕度以保证构件的使用寿命，因此，在结构设计时，一般取D<0.5[16]。由图7可知，3条焊缝的最大疲劳损伤值分别为2.18、1.19、5.40，均大于0.5，其中在焊线3焊缝上更容易出现疲劳裂纹，因此，该焊接构架横梁和侧梁连接处不满足疲劳设计的要求。

2.4 基于实测应力谱的疲劳损伤评估

为了验证有限元仿真分析结果的有效性，根据仿真计算结果及疲劳裂纹出现的位置，在焊接构架横梁和侧梁连接处布置应力测点，其中焊线1焊缝测点位置位于节点12附近，为测点1；焊线3焊缝的测点位于节点2处，为测点2，测点布置见图8。应变片采用全桥方式布置，以消除环境温度和测试导线电阻对数据信号的影响。

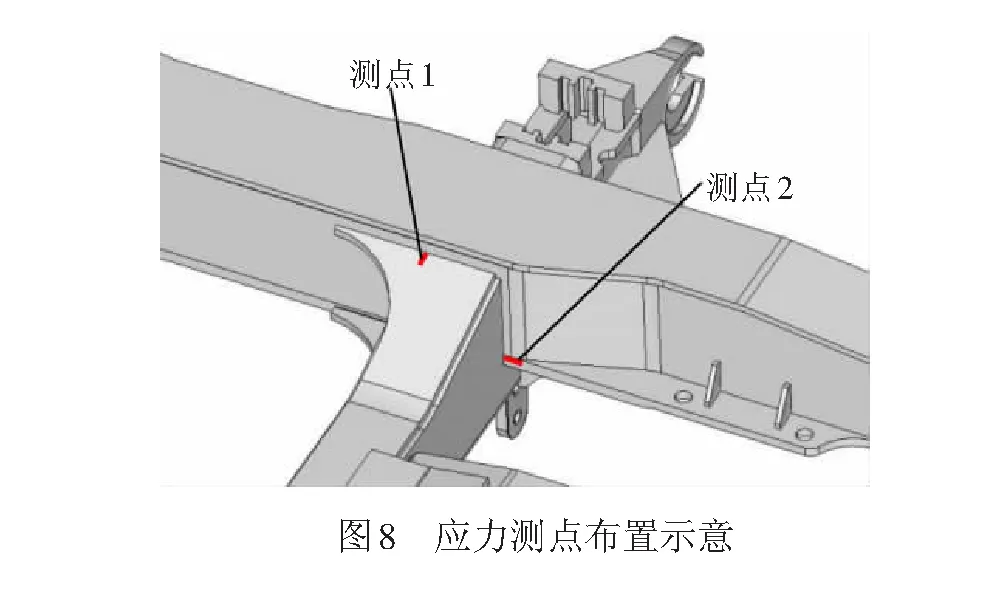
试验过程中采用Imc公司的动态数据采集系统在大连至赤峰区段往返进行线路运营测试试验，设置采样频率为1 000 Hz，以确保试验数据的完整性。采用雨流计数法对应力-时间历程进行数理统计并编制应力幅值谱，在数据处理过程中忽略小幅值应力的影响，最后得到焊接构架横梁和侧梁焊缝连接处各测点的应力幅值谱，见图9。

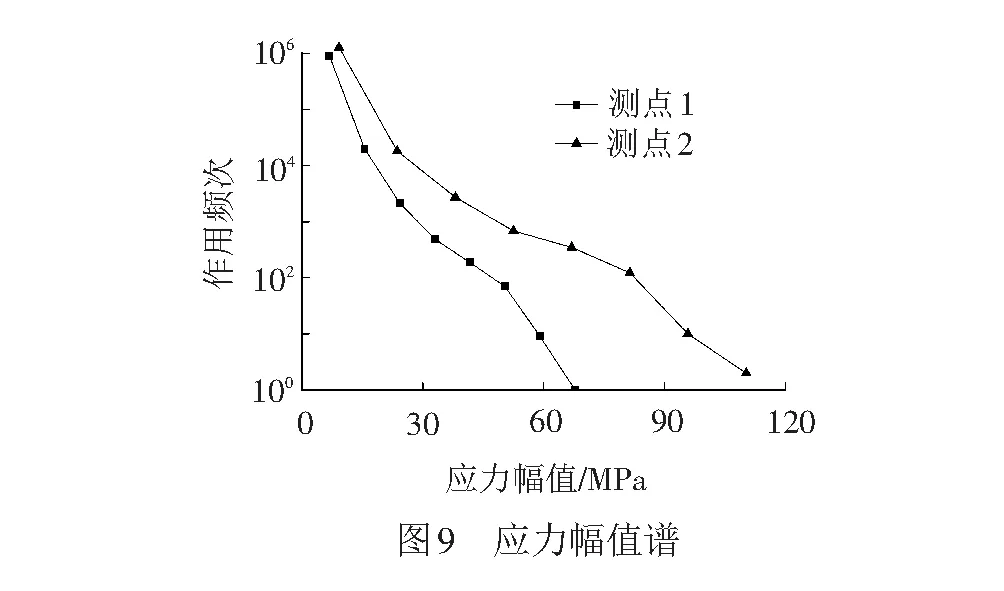
根据Miner线性疲劳累积损伤法则和材料S-N曲线[17-18]，推导出应力谱块的损伤公式为

(16)

式中：D1为实测应力谱产生的损伤；C1为材料S-N曲线的参数；ni为各级应力水平对应的应力循环次数；m0为材料S-N曲线的指数；σi为各级应力水平的幅值；Ki为对应于当前载荷水平的疲劳寿命；k为一个载荷谱的级数。考虑有限元仿真计算时所选载荷偏保守，式中C1、m0的取值参考文献[19]中焊缝F级的相关参数[4]。

已知运行L1的实测应力谱产生的损伤为D1，设在实际载荷下运行L(结构寿命内的总里程)产生的损伤为D，则

(17)

根据式(16)、式(17)及图9可得构架横梁和侧梁焊缝连接各测点的疲劳损伤值，见表4。

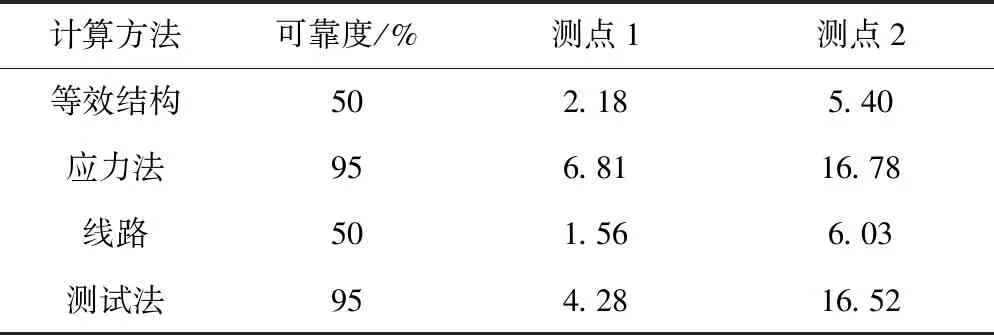
表4 各测点疲劳损伤值

由表4可知，线路测试中测点1和测点2处的疲劳损伤值均大于0.5，且测点2位置更容易发生疲劳破坏，这与等效结构应力法的分析结果相一致，同时在一定程度上也验证了采用等效结构应力法对焊接结构进行疲劳损伤分析和寿命评估时具有较高的精度和可靠性。

3 结论

本文针对某焊接构架在运用过程出现的疲劳裂纹问题，采用等效结构应力法和线路试验法对该型构架进行疲劳分析，主要结论为：

(1) 从文献中选取的对比数据表明，等效结构应力法具有网格不敏感特性，与其他传统焊接结构的疲劳评估方法相比，该方法具有较高的可靠性和适用性。

(2) 基于等效结构应力的仿真计算和线路测试的分析结果表明，该型转向架构架横梁和侧梁连接焊缝处的疲劳损伤值大于0.5，该转向架构架不满足疲劳设计的要求。

(3) 采用等效结构应力法计算得到该焊接构架关键焊缝的疲劳累积损伤与线路试验结果具有较好的一致性，表明等效结构应力法对焊缝部位的疲劳寿命分析具有较高可靠性，研究结果为正确使用规范及制定符合我国线路条件的设计规范提供了参考和依据。