基于射流的高速列车受电弓空腔气动噪声降噪方法

黄凯莉，袁天辰，杨 俭，苗晓丹，宋瑞刚

(上海工程技术大学 城市轨道交通学院， 上海 201620)

列车速度的快速提升，引发气动噪声的危害日益显著。由于运动中的气流受到列车表面凹凸不平位置的影响，两者碰撞引起剧烈的远场空气脉动压力场的变化，从而引发成气动噪声问题，其声压等级也会随车速以6～8次方比增加[1-2]。结合近远场的气动噪声特性来看，受电弓底座及绝缘子区域是受电弓主要噪声源[3-5]，列车速度达300 km/h时，受电弓底座声压级值可达到151.7 dB，仅次于弓头部位总声压级值156.3 dB，并且有较多的低频噪声[6]。由此可见，如何有效减少受电弓底座部位的气动噪声迫在眉睫，同时也是列车降噪的关键所在。

目前对气动噪声研究中有被动及主动2类降噪方法。被动降噪指在流场中无外部能量输入，国内外研究中有优化几何结构(如优化弓头截面形状[7-9]、优化受电弓绝缘子截面形状[10]等)、材料属性(圆柱杆件采用多孔材料[11]等)、安装导流罩(施加导流罩[12-14]等)、仿生改形设计(圆柱杆件表面做仿生改形设计[17-18]等)、受电弓的开/闭口方式[15-16]来影响局部流场运动状态，其中SUEKI等[11]通过改用多孔材料，再经过风洞仿真实验。最终结果表明，列车车速为360 km/h的噪声值降低了1.9 dB；张亚东等[15]对受电导流罩结构和位置、弓开/闭口方式进行优化，最终将噪声值减小了3.1 dB。主动降噪指增加外部能量，使局部流场发生变化，来进一步影响气动噪声值的变化。Mitsumoji等[19]为了达到减少窄频带噪声目标，于弓头处引入主动激励器。目前国内外主要用被动降噪对受电弓进行降噪研究且降噪效果有限，而对其主动降噪研究还处于初级阶段。本文提出一种基于射流的受电弓主动降噪方法，针对受电弓空腔区域做相关降噪仿真分析。

本文通过建立3节车编组高速列车简化数学模型，利用定常剪切应力传输模型SST k-w计算高速列车周围稳态流场，得到了降噪前后流场静压力图，以及空腔内速度流线图与粒子轨迹图，同时进行大涡、FW-H 声学比拟理论以及FFT模拟仿真；通过计算得出相应远场气动噪声，研究空腔部位的噪声特点，并分析在2个不同射流方向下的气动噪声具体表现情况。

1 气动噪声计算模型

1.1 几何模型

基于CRH380B型高速列车做仿真分析，对列车车身进行建模，并对该车身作一定的简化处理，主要由2辆拖车(头车和尾车)、中间1辆带受电弓动车构成，头车车顶设置了2个导流罩。模型选用我国高铁线路上普遍应用的单臂受电弓，并带有安装受电弓用的车顶凹槽。重点分析受电弓与空腔的噪声流场，因射流降噪对列车底部影响不大，仿真计算过程中简化了列车车辆下半部分，包括转向架及车门等系统。以CX-NG型列车受电弓作研究对象，同时将受电弓模型做略微简化，忽略螺栓垫片等细小特征。该仿真模型长76.5 m，宽3.26 m，高3.89 m，高速列车几何模型见图1。

1.2 计算域与边界条件

流场的计算域及边界条件见图2(a)，计算域长306 m、宽78.24 m、高38.9 m，为提高精确度，模拟真实行车环境，将模型置于整个计算域的底部中心位置，忽略列车走行部与地面的间隙，其前端与计算域进口处的间隔为76.5 m(约1节车的长度)，其后端到计算域出口的间隔为153 m(约2节车长)。

计算域设定:进口气流速度v=98 m/s；出口压力为0；模型底面无滑移；车身表面为固定边界。

1.3 网格划分

本文使用Fluent中的ICEM CFD做网格划分处理。其中，车身区域部分进行四面体网格处理，外域部分进行六面体网格处理，其两者连接处设定为interface交界面，进行两者信息交换传送。主要研究受电弓区域，把研究区域的网格再做加密处理，同时设定研究区域最大网格尺寸20 mm；同样列车周围做加密处理；外场设定最大尺寸1 000 mm。经过网格独立性检验，最终划分单元总数约为412万，见图2(b)—图2(d)。

1.4 计算方法

采用基于SST k-w模型做稳态仿真，将瞬态仿真的初始值设置为稳态仿真的计算结果，通过大涡模拟得到瞬态仿真的结果，仿真得到流场中边界脉动压力，再采用FW-H声学比拟理论来求解近场到远场的传播，最后实行FFT，把最终仿真计算结果时域脉动信号转为频域信号。在瞬态仿真过程中，时间步长设定为1×10-4s，共0.2 s(2 000步)。

分析受电弓区域处于高速气流中的声压级值，将其当作声源，共设定A、B、C3列远场噪声监测点。声场计算选用FW-H方程声模拟，计算频率上限设定为5 kHz。

2 数学模型与降噪模型

2.1 数学模型

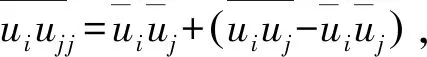
( 1 )

该式右端含有不封闭项

( 2 )

τij为亚格子尺度应力，若达到大涡模拟条件，需构造封闭模式，增加Smagorinsky-Lilly模型，其方程为

( 3 )

( 4 )

( 5 )

其中，Δ代为网格尺寸；Cs是Smagorinsky常数。

初始流场在大涡模拟做瞬态仿真分析中是最为重要的前提，故本文在做稳态仿真时，运用SST k-w模型，具体方程为

( 6 )

( 7 )

( 8 )

式中：vt为涡黏系数；Ω为涡量；y为近壁面间隔；k为湍流动能；ω为湍流比耗散率；σk、σω为k和ω的湍流普朗特数；Vt为湍流黏性系数；v为湍动黏度；a1、γ、β*、σ、β为经验系数;D为运算符号；F1、F2为混合函数，分别为

F1=tanh(ξ4)

其中,

2.2 空腔射流模型

受电弓底座安装部位有几种形式，一种形式是将受电弓安装于车顶空腔内(也称为受电弓沟槽)，见图3。本文将空腔模型做适当简化，其空腔长深比L/D=6.25，是具有代表性的开式空腔[20-21]。

高速运行中的气流在靠近空腔前端处分散，局部分散的气流汇合成剪切层，从而诱发相应漩涡运动，该漩涡按照相应的流速往空腔后端运行，冲击后壁，再引发压力波往回传递；该压力波和空腔前壁发生碰撞，又产生新的漩涡，循环往复产生空腔内自激振荡[22]。空腔噪声产生机理示意见图4。

本文采用的射流装置安装在受电弓空腔处，见图5，射流面设置为宽40 cm，长220 cm。参考余培汛等[23]引入的射流速度为0.1倍来流马赫数的条件，其v=30 m/s，射流面上射流速度保持一致，第一种射流方向与来流方向保持一致，安装在空腔背风面，在此称之为顺向射流，第二种射流方向与来流方向相对，安装在迎风面，在此称之为逆向射流。射流方向位置见图5。

3 射流降噪分析

3.1 近场气动噪声

在车速350 km/h下，表面声功率级分布云图见图6。根据仿真结果，位于车顶的受电弓相比车顶其他位置具有较高声功率级(极值达111 dB)。碳滑板和弓头部位的最高声压级可达111 dB。声功率高的位置，其对应的脉动压力值也会相对较高，同时会引发较高的气动噪声，所以上述2个部位是受电弓部位的主要噪声源。

3.2 涡量分析

射流前后受电弓空腔水平截面，同一时刻下的涡量图对比见图7。降噪前空腔中主要的不稳定区域集中在空腔迎风面附近，漩涡运动抵达空腔后端，和后壁产生碰撞，形成压力波，验证空腔部位引发气动噪声的机理，见图7(a)；引入顺向射流后，使得空腔前端处的涡流较为平缓，也减弱了漩涡撞击空腔后壁的碰撞力度，把局部运动中的气体从空腔后缘导出，见图7(b)；逆向射流的加入，与来流发生碰撞，来流气流在碰撞后从空腔后壁导出，见图7(c)。图7的涡量图对比说明,正向及逆向射流的施加，减小了空腔内气体的碰撞。

3.3 静压力云图

在车速350 km/h下，射流前后受电弓空腔部位的静压力分布见图8。由图8可得出如下结论：

(1) 弓头、底架、平衡杆和绝缘子等为受电弓的主要静压力部位，空腔静压力范围在3 580～6 950 Pa之间，其中空腔后端气动噪声的脉动压力幅值有较大的变化，见图8(a)。

(2) 施加顺向射流后，空腔后缘有较大的静压力，相对于射流前流场，空腔后缘部分的最大静压力从6 950 Pa降到4 520 Pa，下降了34.9%；在逆向降噪后，空腔的后缘部分的最大静压力从6 950 Pa降到5 450 Pa，下降了21.6%，见图8(b)、图8(c)。

3.4 速度流线分析

受电弓空腔速度流线见图9。由图9可知，射流前空腔后壁及前壁尾流较为复杂，易形成分离流动，导致这些位置的压力变化比较剧烈；加顺向射流后，空腔前壁、中部以及后壁流线图较为稳定；加逆向射流后，来流的气流与射流的气流在空腔中部相撞，在空腔中部形成一定的涡流。较明显的是，加顺向射流后，最快速度由原来81.1 m/s降到69.6 m/s。

3.5 粒子轨迹图

降噪前后粒子轨迹见图10。由图10可见，降噪前粒子在空腔内轨迹混乱，形成没有规律可循的漩涡，部分气流在空腔底部滞留；加顺向射流后的粒子轨迹较为平缓、清晰，顺向射流的加入将一部分向后流动的气体从后空腔中导出，能更好的减弱气流到达空腔后壁与之发生的碰撞力度，进而减小气动噪声值；而逆向射流的加入，与来流在空腔中部碰撞，来流一部分在空腔前缘回旋，一部分到达空腔底部后从空腔后缘导出。顺向射流可明显改善粒子在空腔内的流动。

4 远场气动噪声分析

根据稳态流场的分析，构建与之对应的远场气动噪声监测点，基于瞬态下噪声值，分析得到相应的声压信息，最后针对该声压信息做快速傅里叶变换。本文共设置A、B、C3列噪声监测点，分别距离轨道中心线3.5、7、25 m(共13个监测点)，相对地面高度3.5 m，按顺序各列由下至上设定成3、2、1，例如A处监测点A1、A2、A3，见图11。

射流前后标准监测点(C列)的气动噪声总声压级见图12，可得出以下结论：列车速度350 km/h下，C列标准监测点，降噪前、顺向射流和逆向射流3种工况的平均总声压级值依次是78.02、71.98、77.89 dB。施加顺向射流后，其平均总声压级比降噪前下降了6.04 dB；施加逆向射流后，其平均总声压级比降噪前下降了0.13 dB。

各个位置监测点相应的平均总声压级见表1。从表1可以看出：施加顺向射流后，空腔附近监测点平均总声压级小于施加逆向射流时相应监测点平均总声压级，车速达到350 km/h时，施加顺向射流的降噪效果最为显著。

表1 各个位置监测点的平均总声压级 dB

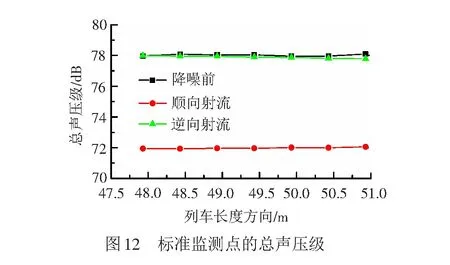
监测点C4处射流前后的声压级频谱图见图13，由图13可得：高速列车受电弓部位产生宽频噪声，处于低频段时声压级值达到高峰，并且随频率的增加，其声压级值不断减小。射流前、顺向射流和逆向射流在100 Hz低频内，各自的最大声压级值分别是57.09、62.81、61.41 dB。

每个频段发出的噪声对人耳产生的影响是不同的，人们能敏锐感受到的频率是500～6 000 Hz范围内。本文采用A计权声压级衡量方法，见图14。

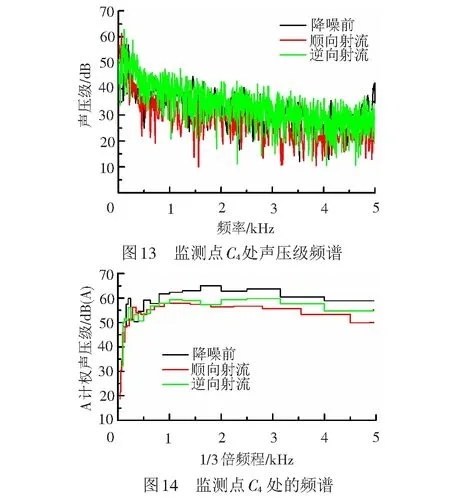
由图14可知：

(1) 施加射流前后，监测点气动噪声的能量重点集中于700～5 000 Hz频率内，并且监测点处A计权1/3倍频程图呈现出相似规律，在低频时A计权声压级值迅速增大，随后变化幅度较为缓慢，趋于平稳。

(2) 射流前在高频1 600 Hz处出现最高峰值65.03 dB(A)；施加顺向射流后，在低频900 Hz处出现最高值57.89 dB(A)，随着频率增大，A计权声压级值趋向于稳定；施加逆向射流后，在高频2 500 Hz处出现最高峰值59.85 dB(A)。射流在该点处抑制高频段的声压级较为明显。

由上述分析可知，空腔逆向射流的加入，减小了漩涡与空腔后壁的碰撞，然而由于逆向射流与来流相撞产生新的漩涡，同时漩涡也影响空腔前缘的剪切层，远场气动噪声监测点(C列)平均总声压级值降低了0.13 dB。空腔内引入顺向射流，部分射流将运动的气体从后空腔中导出，另一部分射流减小了漩涡与空腔后壁的碰撞程度，同时减少了空腔内部自激振荡的过程，远场气动噪声监测点平均总声压级值降低了6.04 dB。综上所述，在受电弓空腔处施加顺向射流有明显降噪效果。

5 结论

本文提出了一种基于射流的受电弓空腔主动降噪方法，对空腔部位做仿真分析，根据SST k-w模型和大涡模拟对受电弓底座与空腔部位做计算分析，同时比较2个射流方向的降噪效果。数值计算结果表明，顺向射流降噪效果较为显著，射流降噪对高速列车节能减排、减阻降噪具有重要意义。基于有限元仿真结果分析，得出以下结论。

(1) 受电弓系统是高速列车主要噪声源，气动噪声聚焦产生在受流碳滑板、弓头以及底架，其中弓头部位的静压力值为6 950 Pa，底座静压力值为5 820 Pa，由此可见在受电弓底座区域做降噪很有必要。

(2) 施加顺向射流后，由于射流对空腔漩涡的影响，从而改变空腔内的压力分布，减弱了漩涡与空腔后壁的碰撞，将一部分流动的气体从后空腔导出。经仿真验证，本文采取的模拟方法所模拟的空腔流动状态与空腔流动机理是相吻合的，证明了顺向射流主动降噪具有一定可行性。

(3) 施加逆向射流后，减小了漩涡与空腔后壁的碰撞，逆向射流与来流相撞产生新的漩涡，新的漩涡一部分向后空腔导出，一部分影响空腔前缘，空腔后缘部分的最大静压力从6 950 Pa降到5 450 Pa，下降21.6%。

(4) 远场标准监测点平均总声压级为78.02 dB。加入顺向射流后，射流改变剪切层与后壁的碰撞强度，远场气动噪声监测点平均总声压级降幅为6.04 dB，作为对比，施加逆向射流后，平均总声压级降幅为0.13 dB。因此，顺向射流降噪效果比逆向射流降噪效果显著。