基于有限元法的高速铁路接触网吊弦动态特性研究

2020-07-30吴文江高占凤骆祥坤

铁道学报 2020年7期

吴文江，李响, 高占凤, 骆祥坤

(1. 石家庄铁道大学机械工程学院，河北石家庄 050043; 2. 石家庄铁道大学工程训练中心，河北石家庄 050043)

高速铁路运行中，受电弓与接触网通过滑动接触方式相互作用，从而完成电力传输。吊弦作为接触悬挂中承力索与接触线的连接环节，将接触线所承受的非等幅阻尼振动传递至承力索上，吸收和缓冲承力索及定位点所受的振动冲击。吊弦一旦发生断裂，将导致接触网几何参数发生变化，影响列车取流及安全运行。近年来，武广、京广、京沪等高速铁路均有整体吊弦断股、折断现象发生[1]。因此，分析吊弦的动态行为，对于改善吊弦工况、提高列车运行安全性具有重要的研究意义。

Park等[2]利用有限元法，对行车速度为100～400 km/h的弓网作用情况进行仿真计算，研究发现：通过优化受电弓参数，可以达到有效改善弓网振动特性的目的。文献[3-4]建立受电弓-接触网有限元模型，结合直接积分法对不同行车速度下的弓网系统进行仿真计算，研究发现随着速度增加，离线率也随之增加，并得出无离线现象发生的最大车速在250～300 km/h之间的结论，同时还指出：通过优化受电弓刚度、阻尼、静抬升力、接触线张力等参数，可以降低弓网系统离线情况的发生。陈立明[5]以现场测试吊弦动态抬升量为初始载荷，基于有限元法对接触网进行瞬态动力学分析，结果表明：整体吊弦动态力波动较大，约为静态力的6倍；定位点附近吊弦力波动最大，受压幅度最大，容易发生疲劳破坏；跨中吊弦受压频率最高。但文中认为吊弦对称排布，导致相对于跨中对称位置上的吊弦受力情况相同，忽略了接触网自身波动传播具有方向性所造成的影响。戚广枫等[6]通过对弓网系统进行仿真计算，得到了250、300 km/h双弓情况的吊弦静、动态应力结果，并利用数值模拟等方法处理成疲劳载荷谱，研究表明：跨中位置吊弦最易出现疲劳断裂；车速越高，疲劳断裂概率越高。Liu等[7]通过对现场断裂吊弦进行断口形貌分析实验，并结合接口压紧力仿真分析，得出结论：压紧力过大导致的局部铜导线截面减小所引发的应力集中是引发吊弦断裂的原因之一。

综上所述，目前已有研究中对吊弦具体服役工况下动态行为缺少深入研究，断裂结论尚未统一。因此，本文基于有限元法对弓网系统进行瞬态动力学分析，确定各位置吊弦服役工况与所产生故障的联系，为改善吊弦断裂情况、优化接触网波动特性提供有效方案。

1 弓网耦合动力学方程

接触网跨距大，承力索和接触线的抗弯刚度都较小，属于柔性结构，呈现出明显的弦特性，故跨内的不同位置其刚度存在差异[8]，因此一般将其视为变刚度弹性系统。取流核心部件受电弓主要由弓头、上框架、下框架组成，是一个变系数的带有平方项的非线性系统，本文采用典型的三自由度受电弓系统模型对其进行线性化处理。二者耦合状态示意见图1。

图1中,Ft为弓网接触力；F1为静抬升力；F2、F3为空气抬升力；m1、m2、m3分别为下框架质量、上框架质量、弓头质量；k1、k2、k3分别为下框架刚度、上框架刚度、弓头刚度；c1、c2、c3分别为车体与下框架阻尼、上下框架间阻尼、弓头阻尼；kt为接触网刚度。利用最小二乘原理对接触网刚度非线性数据进行曲线拟合[9]，得到接触网刚度为

( 1 )

( 2 )

式中：α1～α5为拟合系数；k0为接触网平均刚度，N/m；v为机车行驶速度，m/s；L为接触网跨距，m；L′为相邻吊弦距离，m；t为系统时间，s。

根据图1建立弓-网耦合动力学方程

-Ft+F3

( 3 )

( 4 )

c1y1+k1y1=F1

( 5 )

式中：

Ft=kt·y3

( 6 )

则式( 3 )可改写为

( 7 )

式中变量与图1一致，相关参数取值见表1。代入参数，对速度为250、300 km/h 2种情况做10 s仿真计算，求解接触力、抬升量的变化情况，仿真结果见图2、图3。

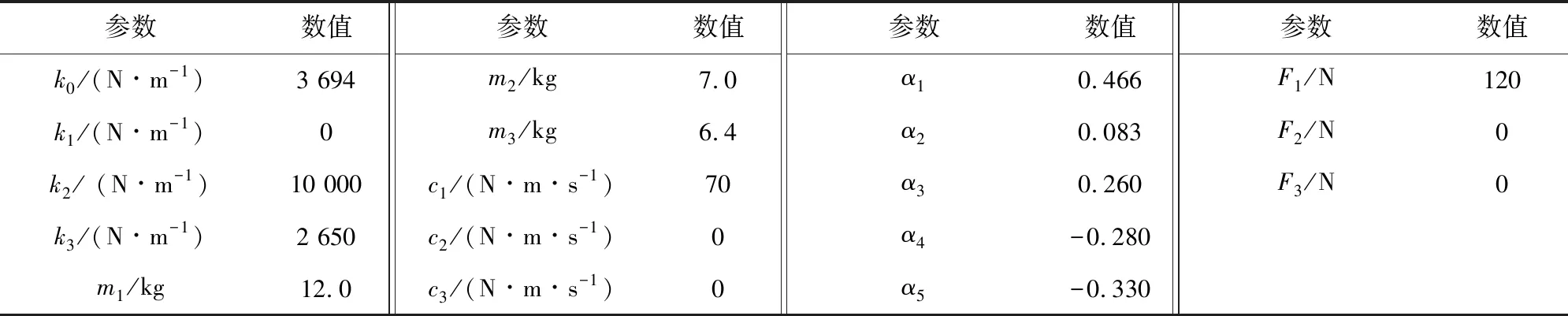
表1 弓网耦合模型参数

根据欧洲标准EN 50318—2002[10]所提供的速度250、300 km/h 2种情况下的仿真标准对计算结果进行有效性验证，结果见表2。

表2 模型有效性验证

由表2可知，仿真结果在EN 50318—2002许可范围内，仿真结果具有有效性。从图2、图3的仿真计算结果来看，抬升量相比于接触力，波动变化更为稳定平滑，作为载荷输入更容易在接触分析时达到收敛要求。因篇幅有限，仅对时速250 km/h情况下单跨抬升量波动曲线进行线性拟合，拟合结果见图4。利用拟合的载荷谱，作为之后瞬态动力学分析中的受电弓抬升量变化输入。

2 弓网耦合瞬态动力学仿真

以往研究常将吊弦视为质量-弹簧单元模块，将质量平均分布在接触线与承力索上[11]，这种方法虽可以降低计算量，但无法真实准确地反映列车经过时吊弦的动态行为。为了显示受电弓通过单跨接触网全部时间历程内的吊弦响应结果，利用Ansys WorkBench中包含时间维度的瞬态动力学模块对弓网耦合系统进行仿真。本文采用结构高度1.2 m、跨距64 m、吊弦间距8 m的简单链型悬挂接触网作为研究对象，利用分模法[12-13]进行接触网初始状态求解：将接触悬挂分解成接触线与承力索2个部分，先根据接触线无弛度静态模型，计算求解此条件下吊弦受力结果；再根据吊弦受力与承力索所受自重的叠加状态求解承力索变形，进而确定吊弦长度，最终完成整个接触悬挂的几何参数确定。接触网结构参数见表3。

表3 接触网结构参数

根据结构参数创建接触网静态几何模型，导入WorkBench后将其设为柔性体，承力索两端定位处固定且无相对转动，接触线两端定位处垂向位移为0，可以平面转动，二者材料属性及补偿张力参数见表4。本文不考虑受电弓形变，将其作为刚性体处理以简化计算量。承力索、接触线及吊弦结构均属于简单几何体，利用扫略生成六面体网格，承力索扫略尺寸500 mm，共计512个单元；接触线扫略尺寸100 mm，共计3 200个单元；吊弦扫略尺寸50 mm。

表4 接触网线材参数

利用Workbench中接触分析模拟受电弓与接触线之间的相互作用关系。接触分析是对空间上多个物体相互接触但无法彼此渗入贯穿所进行的状态非线性分析，有限元理论中基于罚函数法进行计算，罚函数为

Fnormal=kknormal·xpenetration

( 8 )

式中：Fnormal为接触力；knormal为接触刚度；xpenetration为渗入量。

式( 8 )中，当knormal理想无限大或xpenetration足够小时，即可模拟弓网之间接触力的传递关系。

接触示意3模型及罚函数求解原理见图5。利用对受电弓相对于地面设置位移运动副的方式模拟列车运行取流过程，将图4载荷谱作为移动点载荷输入，其中水平轴数值模拟列车行驶过程，垂向数值模拟受电弓抬升、下落过程。弓网接触属于刚柔耦合状态非线性问题，二者之间的接触存在大形变和相对滑动，接触网刚度每个瞬间发生的形变都将引起其自身刚度的迭代变化，求解过程通过Newton-Raphson法迭代完成。由于接触网跨距尺寸大，求解过程难以收敛，为解决此问题，需对载荷步长及接触参数进行精确调试设置，参数设置见表5。

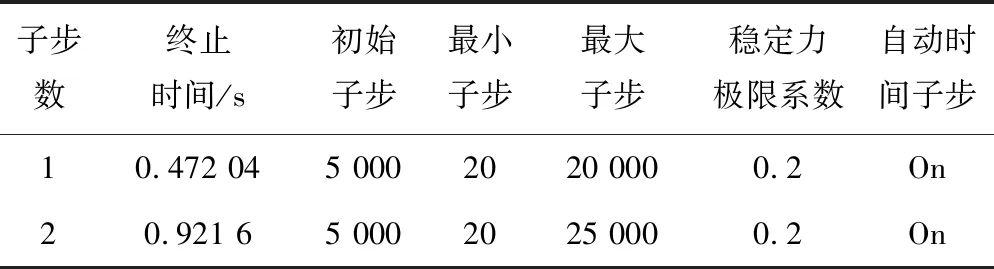
表5 有限元参数设置

3 结果与分析

3.1 吊弦振动形变分析

吊弦振动受接触线形变驱使，自下向上传递，由于自身材料阻尼特性，波峰逐渐变小，故最大振幅在靠近接触线一侧。提取各吊弦最下端单元的全部时域下的空间位置坐标，即可确定振动源运动轨迹，结果见图6。图6中，X轴负半轴为列车行驶方向，Y轴表示左右方向，Z轴表示垂直地面方向，正半轴为向上。

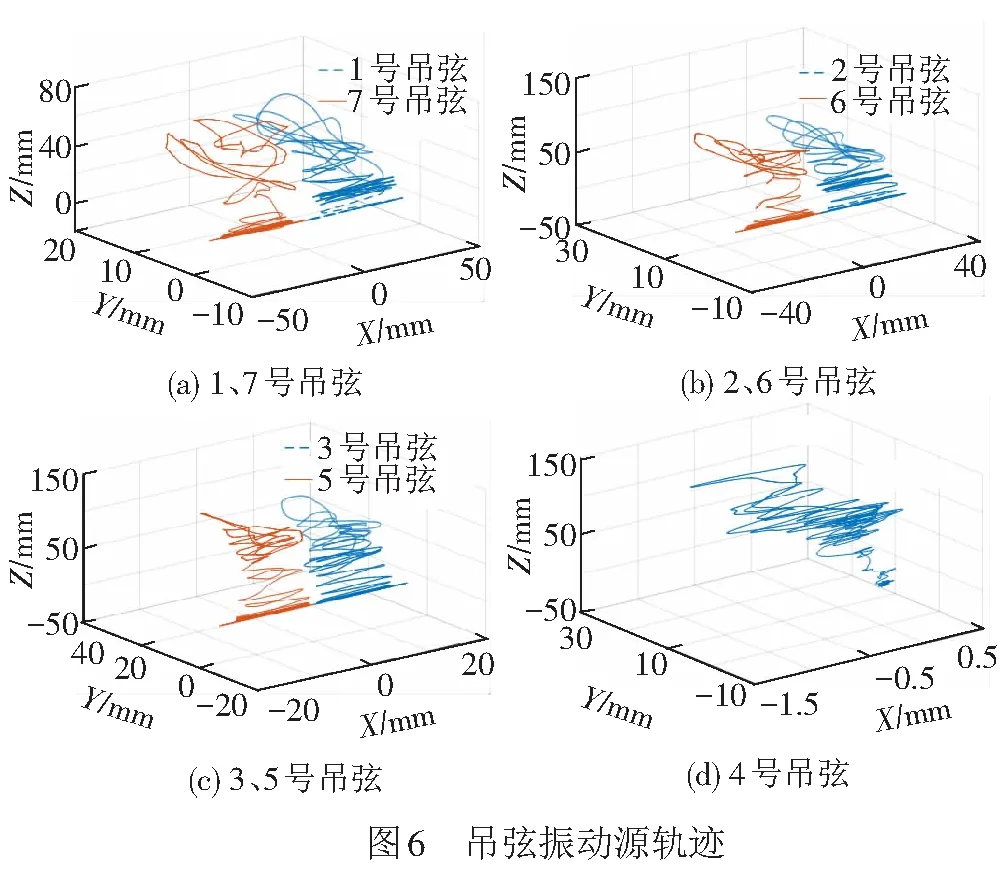
由图6可以看出，相对于跨中位置对称分布吊弦的振动源，在Y、Z轴方向运动规律基本一致，1、2、3号吊弦振动源产生X正半轴形变，5、6、7号吊弦振动源产生X负半轴形变，幅值基本相等。这是因为接触线的形变实际是围绕两端定位点发生的微转动，由于抬升量向上，则左半侧的接触线实际做绕左侧定位点逆时针微转动，其上方的连接点向X负半轴发生位移；右半侧接触线做绕右侧定位点顺时针微转动，其上方连接点向X正半轴发生位移，4号吊弦处于跨中位置，故出现反复波动的现象。从运动规律上来看，吊弦位置越靠近跨中，吊弦压缩幅值越大，振动频率也增大；压缩产生初期，运动以前后摆动为主，越靠近定位点的吊弦前后摆动越大，魏超等[16]认为吊弦下端过大的摆动会加剧与钳压管之间的摩擦，从而引起微动弯曲疲劳的发生，使疲劳裂纹提前萌生并加速扩展，最终导致吊弦过早断裂，见图7(a)；压缩值逐渐增大后，吊弦开始出现明显的左右摆动，这是吊弦在过大抬升作用下处于松弛状态，下端约束力降低所导致的，当左右横摆过大时，将扩大弓网之间的摩擦范围，加剧弓头磨损、降低接触线使用寿命，使取流质量受到影响，见图7(b)；4号吊弦在小幅度压缩时，振动源各方向位移较小，随着压缩幅度增大，其各方向摆动幅值也逐渐增大。因为位于接触网跨中位置，距离约束点最远、柔性最大，故4号吊弦振动频率及幅值也大于其他位置的吊弦，这说明其承受的疲劳断裂风险也最高。另外，高频振动还容易造成线夹螺栓止动环松动，从而引起载流环下垂，干扰列车正常取流，见图7(c)。

对图6中振动频率及运动轨迹在X、Y、Z方向上的最大值和平均值统计分析见表6。表6中可以看出，振动频率由两端向中间逐渐增高；振动源的X方向最大形变值和平均值从接触网跨两端向中间逐渐减小，Z方向上，越靠近中间位置抬升量越大，4号吊弦的垂向形变约为1号、7号吊弦的2倍，这表明两侧吊弦对于水平方向摆动更为敏感，跨中位置吊弦则对垂向抬升更为敏感，且振动频率更高。Y方向横摆平均值、最大值变化不明显，说明左右摆动情况受吊弦位置影响不大。

表6 振动轨迹统计

3.2 吊弦压缩弯曲形变分析

吊弦垂向上存在2种状态，即静态拉伸与受压弯曲。当受电弓距离分析跨较远时，各位置吊弦由于承受自身重力以及接触线重力，处于静态拉伸状态；当受电弓滑入分析跨内，引起接触线抬升，此时吊弦处于受压弯曲。通过提取吊弦与承力索、接触线间共享节点的垂向位移L1、L2，计算2点垂向位移差得到每根吊弦的具体状态，即

L2-L1>0

( 9 )

L2-L1≤0

(10)

式( 9 )表示受压弯曲状态；式(10)表示拉伸状态。七根吊弦压缩计算结果见图8。

由图8可以看出，受电弓经过跨内时长不足1 s，接触线形变恢复不充足，吊弦始终处于受压弯曲状态；各位置吊弦的弯曲变化频率基本一致，约为10 Hz；时域上，各吊弦初始受压弯曲的产生时间存在明显的滞后性(图中黑线标出)，1号吊弦最早产生受压弯曲，随后自左向右依次发生；越靠近跨中位置吊弦受压弯曲程度越高，4号吊弦受压弯曲程度最大，约为120 mm。吊弦由多股铜丝绞制而成，整体上存在因绞制而产生的具有方向性的内力，当受压弯曲形变过大时，外力约束减小，内力占据主导位置，容易造成吊弦扭结，见图9(a)。扭结后的吊弦在受电弓经过后由于无法恢复至原本长度，将引发接触线长期形变、受流中断的诸多状况。扭结严重时，还会引发吊弦局部塑性变形，从而造成吊弦松弛现象，见图9(b)。

3.3 吊弦弯曲特性分析

由3.1、3.2节可知，吊弦动态特性是振动形变与压缩形变二者共同作用的结果。结合图6、图8来看，压缩幅值为水平方向形变量数倍，说明单根吊弦内存在多个弯曲点，仅通过最大形变值并不能说明吊弦的真实弯曲状态，因此需要进一步计算曲率加以说明。3.1、3.2节提到4号吊弦压缩幅值、水平形变值均为所有吊弦中最大，以4号吊弦为例进行弯曲特性分析研究。提取4号吊弦上12个间距为40 mm的等距节点，作为形变的特征点，X轴零点为接触线与吊弦连接点位置坐标，向上至承力索方向为正方向，Y轴为时间，Z轴为弯曲形变量，利用吊弦的每个节点的形变结果生成吊弦弯曲形变时域图，见图10。

2.提高文化业务素质，认真履行工会职能。作为工会干部，要努力提高洞察能力，塑造优秀的人格形象，掌握有关法律、法规和政策；了解企业的经营情况。还要有刻苦钻研的精神，要精通业务，吃透有关工会工作基本理论和相关的知识。熟悉工会工作的特点与规律，自觉贯彻执行工会工作方针和总体思路，全面履行工会的基本职能，善于将工会工作与单位的中心任务结合起来，只有这样，工会说话办事才有底气，在群众中才有号召力，才能使工会工作开展得正确规范，富有成效。

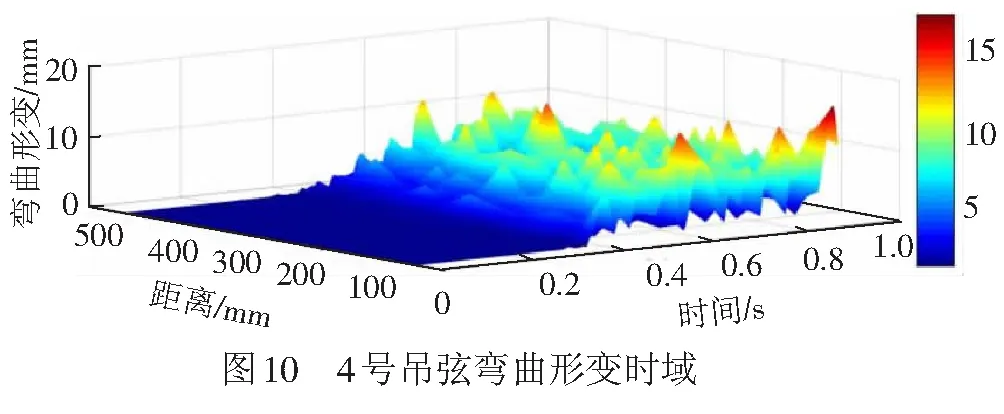
由图10可以看出，整个时域下的形变结果分成两部分，0.3 s之前，4号吊弦上各个位置的节点弯曲形变几乎为零，这是因为4号吊弦位于跨中位置，接触线弛度最大，当受电弓距离吊弦正下方较远时，引起该位置抬升量较小，未造成吊弦大幅弯曲；0.3 s之后，受电弓划至4号吊弦附近，抬升量开始引起吊弦弯曲形变。数值上来看，后半程弯曲形变均保持在6 mm以上，最大值出现在接触线与吊弦的连接点一侧为16.5 mm。一跨内，吊弦大于10 mm以上的弯曲形变发生16次，按每日100对单弓列车行驶计算，吊弦将发生1 600次反复弯曲。文献[17]通过实验证明：采用冷拉拔成型的铜合金导线，经过强烈塑性变形后，线体表面出现一层超细晶，超细晶塑性低于材料内部组织，在反复弯曲过程中，由于表层与芯部的力学性能差异使得形变发生不协调，将导致其提前断裂。根据云图数据，进一步对4号吊弦弯曲形变情况进行统计，见表7。

表7 弯曲形变统计值

注：表中节点号为4号吊弦上自下向上的12个等距节点；平均值为每个节点位置产生的弯曲形变平均值；最大值为每个节点位置产生的弯曲形变最大值。

以表7中平均值、最大值作为x值，12个节点纵坐标为y值，利用样条差值方法分别模拟吊弦的2种典型的弯曲形变状态，进而确定各弯曲点位置及曲率。结果见表8。

表8 4号吊弦各位置及曲率

采用相同方式处理其余对称分布的6根吊弦，制成所有吊弦的距离-曲率曲线，见图11。

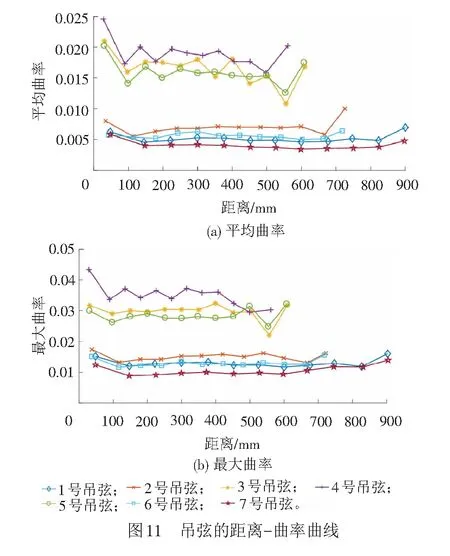
由图11可知，吊弦曲率由两端向中间逐渐增加，其中4号吊弦无论平均曲率还是最大曲率，均高于其他位置吊弦；图11中存在明显的分级现象，3、4、5号吊弦曲率远高于1、2、6、7号吊弦曲率，这说明跨中位置吊弦弯曲程度远大于两侧位置吊弦，伴随着每日过高的弯曲次数累积，其断裂风险也更大；位置对称的吊弦曲率变化情况基本一致，但数值上，后半程的5、6、7号吊弦要稍小于与之分别对应3、2、1号吊弦，这是因为本文针对受电弓的单跨时域内进行仿真运算，后半程吊弦由于受电弓滑动所引发的振动在时间上发生较晚，当受电弓行走过跨内全程后，还尚未完全响应，导致数值上偏小，建议建立连续三跨仿真模型对其进行验证。

3.4 形变方向分析

正常工作状态下，吊弦发生的形变属于弹性形变，当外力或位移载荷减小时，将恢复至初始状态，此过程中的弯曲与回弹均具有方向性，截取受电弓分别划过7根吊弦时各吊弦的瞬时形变速率矢量结果，对其方向进行判断，结果见图12。

由图12可以看出，形变方向呈旋转上升状态，旋转同时存在左旋(黑框内)与右旋2种(红框内)状态。文献[18]中6.5.2小节要求绞线各相邻层的绞向应相反，最外层绞向为右向，因此当吊弦形变方向为右旋时，外丝被加紧，芯丝放松，将导致外丝与芯丝之间相互挤压力增大，严重时芯丝鼓包顶出，影响吊弦力学性能，见图13(a)；当形变方向为左旋时，芯丝之间磨损加剧，外丝出现松股，见图13(b)，严重时导致内外之间产生缝隙，强度整体下降，致使吊弦容易断裂。