基于动态购票需求的动车组重联决策方法研究

詹 彤，单杏花，卫铮铮

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081)

0 引言

高速铁路“一日一图”的运营模式，是根据不同时间段客流需求的大小，实施不同的运行图。在“一日一图”目标下，高速铁路列车开行方案根据市场需求编制，使得需求和运力互相协调。一般情况下，客流较少时实施“常态图”，周五、六、日实施“周末图”，春运暑运和节假日实施“高峰图”。“一日一图”根据市场需求，每日动态调整高速铁路列车开行方案，提高了运输能力投放的精准度，进一步提升广大高速铁路旅客的出行体验。“一日一图”目标下的动车组列车重联开行，是充分利用动车组列车可双向运行、可连挂的特性，在高峰时段实行2 组动车组列车重联编组运行，从而最大限度满足旅客的出行需求[1]。

对于高速铁路列车开行方案的优化研究，国内外学者既有长期优化，也有短期优化，但在短时优化方面还基本处于空白。而且研究一般都是侧重在旅客需求预测、开行成本测算以及开行方案优化模型方面。桂文毅[2]采用灰色线性回归模型、王煜等[3]采用Adaboost-CART 模型，进行客流预测的相关研究，以及MATSUMOTO 等[4]采用独立成分分析和时间序列分析等对高速铁路的旅客需求波动预测。CLAESSENS 等[5]利用二元决策变量整数线性规划模型对铁路客运专线成本进行优化分配。左大杰[6]给出确定性多目标绝对约束模型，设计基于随机模拟的遗传算法对铁路旅客列车开行方案进行研究；史峰等[7-8]建立客运专线相关旅客列车开行方案的多目标优化模型，在此基础上，给出旅客列车开行方案优化的双层规划模型。

目前，高速铁路“一日一图”重联开行决策已经成为铁路运输发展所面临的时代命题。通常情况下，“一日一图”开行方案决策一般会采用效益测算方式决定开行方案的可行性，即测算高速铁路列车开行的盈亏点，达到或超出高速铁路列车盈亏点则认为方案可行。由于动车组列车开行成本具有可计算性，基于效益测算的“一日一图”开行方案决策可以转化为客流预测问题，而客流预测的不准确性导致基于效益测算进行“一日一图”决策，需要通过专家介入进行交互处理。因此，考虑管内动车组列车旅客购买车票的行为特点以及管内动车组列车决策的时效性因素，研究基于动态购票需求的铁路动车组列车重联决策方法，避免采用传统基于效益的决策方法对客座率以及成本的复杂计算。

1 动车组列车重联决策模型

1.1 动车组重联

从动车组列车自身的特点出发，采取动车组列车重联运行的组织措施，虽然原理简单，却有着显著的扩能效果[9]。当区段现有运输能力不能满足旅客需求时，应用重联运输，可以减少乘务人员数量，减轻乘务人员的劳动强度，还可以增加动车组列车的运输能力。一趟动车组列车由原来的8节车厢变为16 节，使得运能翻倍，能够更好地与运输需求相适应。

然而，动车组列车重联运行作为扩能措施仍然存在不利因素，尽管动车组列车重联能够减少线路通过能力对旅客需求的限制，但也需要更多地关注客流本身的变化情况，以及动车组列车开行对客流的满足情况。当客流量足够大，在不考虑动车组列车发车频率的条件下，重联运行可以将动车组列车的输送能力扩大1 倍，加倍满足客流需求。但是，对于某些客流情况经常发生变化的线路，如果动车组列车盲目重联，很可能造成上座率不足而导致亏损运行，在这种情况下应结合客流变化，除灵活重联和摘解动车组列车，还应考虑动车组列车基本是在始发站组织单组或重联，而不在中间站进行摘解和重联。另外，由于跨局动车组列车在重联决策时链条环节多且复杂，因而一般都在各铁路局集团公司管内实施真正意义上的“一日一图”。

铁路局集团公司实施动车组列车“一日一图”决策时，基本是在周二来确定下周的动车组列车日开行方案，实际上还有很多在前两天甚至当天决策开行动车组列车的情况，其中，广深城际铁路(广州—深圳)通常会在周五下午或放假前一天下午，根据客流临时增开动车组列车；中国铁路南昌局集团有限公司(以下简称“南昌局集团公司”)管内，根据售票态势提前一天或当日增开动车组列车已经形成常态。而且，动车组列车由单组变重联相比增开协调难度小，更易于铁路局集团公司执行。

1.2 购票拟合需求模型

2019 年我国动车组列车发送量23.3 亿人次，占全国铁路发送量的65.3%，而管内动车组列车发送量又占全国动车组列车发送量的46.0%。由于我国高速铁路运输能力的大幅增加，旅客出行计划周期缩短，因此不论是长途的还是短途的动车组列车，旅客日常的购票规律一般都是距开车前两天内开始购票。分析日常京沪高速铁路(北京南—上海虹桥) 30 d 预售期内的购票规律发现，66.68%的车票均是在距开车前两天内售出；分析日常沪宁城际高速铁路(南京—上海) 30 d 预售期内的购票规律发现，72.84%的车票均是在距开车前两天内售出。基于此，管内动车组列车的“一日一图”重联决策，在距开车前两天内开展研究。

为确定“一日一图”的管内动车组列车是否需要重联，需要观察距开车前两天(49 h)内动车组列车单组运行和重联运行时的旅客购票需求规律，构建管内动车组列车的购票模型，依据购票模型，推算动车组列车潜在的客流需求。

管内动车组列车的售票规律具有明显的阶段特征，以自然日为周期，午夜零点左右售票值归零，而在中午或下午到达单日内高峰。由售票规律，并根据开车时间划分为3 段，分别对其进行拟合分析。分析开车前两天内实际售票数据，可以得到第一、二、三段分别符合幂函数、二次多项式函数、一次线性函数规律。用xi表示距开车ih；yi表示i- 1 到ih 之间的售票张数。通过对xi，yi进行拟合，构建管内动车组列车购票模型。设距开车小时数为x，单小时内的旅客购票张数为y，建立x，y间的函数关系为

式中：f(x)表示购票-时间函数；a1，b1，c1，a2，b2，c2，a3，b3表示系数，通过各段拟合得到；t表示开车时间，取整数。

进而可以得到开车前两天内的购票需求Y为

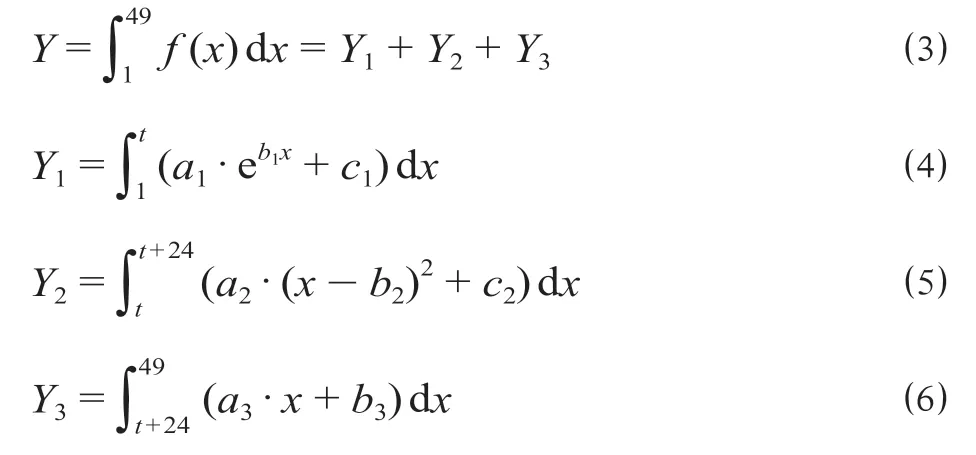
式中：Y1，Y2，Y3分别为第一、二、三分段内的购票需求。

1.3 基于购票拟合需求的动车组重联决策模型

管内动车组列车“一日一图”重联开行决策时，基本分为2 种情况，一是同期已开行单组或重联动车组列车，决策本期应该是单组或重联；二是同期未曾有开行动车组列车，决策本期开行时是单组或重联。

因此，需要依据历史同期数据分别计算单组和重联时，构成分段函数的系列参数，分别记为在预售时间进入开车前两天后，利用已发售的小时购票张数，计算分段函数的参数。将参数带入公式3，4，5 和6，可以得到开车前两天内的购票需求Y。进而可以计算购票拟合需求接近单组或远离重联的程度R，计算公式为

式中：Y(1)，Y(2)分别为单组、重联历史参考购票需求，重联参考需求大于单组。

当R< 0.5 时，则决策为单组运行，反之决策为重联运行。R越远离0.5，判定结果越有参考价值。特殊情况，R= 0.5 的判定结果表示单组重联皆可，此时需要权衡其他因素，根据经验判定单组还是重联，本模型对此情况选择重联。特别地，当R< 0，说明被决策动车组列车的拟合需求比往年单组参考需求还要低，R过低可能单组开行依旧亏损；当R> 1，说明被决策动车组列车的拟合需求比往年重联参考需求还要高，R过高可能重联开行也不能满足全部需求，需要通过增减动车组列车来解决问题。

与R类似地定义R实际，表示被决策动车组列车实际数据与单组参考需求的接近程度，R实际计算公式为

根据R实际判断决策准确度a，直观地衡量决策效果，a计算公式为

2 实例分析

2.1 购票拟合需求数据分析

选取某铁路局集团公司动车组列车在清明节的售票数据，该动车组列车在历史同期单组和重联均曾开行。开车时间为11 : 25，取整之后，t取值11，因此将其在清明节的第一天到第三天分为以下3 段：①1 h ～ 11 h；②11 h ～ 35 h；③35 h ～ 49 h。该动车组列车在2018 年清明节第一、二、三天单组运行，2019 年重联运行。因此，选用清明节前两天作为历史同期数据，将第三天用于验证。

对2018 年清明节前两天数据求均值，得到单组运行数据，根据公式2 所示分布及其系数取值范围，利用Matlab 对单组历史同期数据进行拟合，得到单组参考购票－时间函数的各个参数。观察数据发现，11 h 与35 h 附近，平均售票张数均接近0，为保证第一段指数函数拟合效果，令f(1)(t) =f(1)(11)= 0。得到该车单组参考购票-时间函数为

得到单组参考购票需求Y1(1)= 389.7，Y2(1)=相对误差= 7.66%。

类似地，令f(2)(t) =f(2)(11) = 0，得到重联参考购票－时间函数为

得到重联参考购票需求Y1(2)= 518.9，Y2(2)=相对误差eY(2)= 6.71%。单组与重联拟合图如图1所示。

图1 单组与重联拟合图Fig.1 Fitting graph of single unit and coupled units

2.2 动车组重联决策判定

针对2018 年4 月6 日(清明第三天)进行动车组重联决策判定分析，分3 段进行拟合，在每段上选择合适的时间点，计算购票需求，从而进行重联判定分析。针对每次拟合计算误差，比较判定结果，并计算决策准确度值进行验证。

（1）第一次重联决策判定。由于第三段采用线性拟合，当预售时间进入开车前第45 h，即t+ 34 h 内，选取4 个点，根据第49，48，47，46 h 的售票数据对第三段进行拟合，得到a3I，b3I，并据此进行第一次判定。开车前46 ～ 49 h 分小时售票数据如表1 所示。

根据公式2 所示分布及其系数取值范围，拟合得到第三段的购票－时间函数为

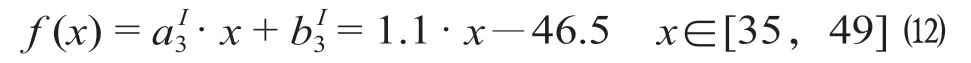
表1 开车前46 ～ 49 h 分小时售票数据Tab.1 Hourly tickets pre-selling volume within 46 to 49 hours before departures

（2）第二次重联决策判定。当预售时间进入开车前第24 h，即t+ 13 h 内，可以根据第25 ～ 35 h的售票数据对第二段进行拟合，并根据第35 ～ 49 h的售票数据对第三段重新进行拟合，得到参数据此进行第二次判定。开车前25～49 h 分小时售票数据如表2 所示。

根据公式2 所示分布及其系数取值范围，拟合得到第三段的购票－时间函数为

对第一次判定时的拟合参数进行修正，得到修正后的第三段购票需求80.266 7，修正拟合相对误差= 6.67%。接下来拟合第二段的购票-时间函数。此时用于拟合的数据均位于拟合后抛物线的右半支，为保证拟合抛物线的形状与历史售票规律相符合，使用单组参考、重联参考函数中的平均值，代替拟合曲线中的参数。

根据公式2 所示分布及其系数取值范围，拟合得到第二段的购票－时间函数为

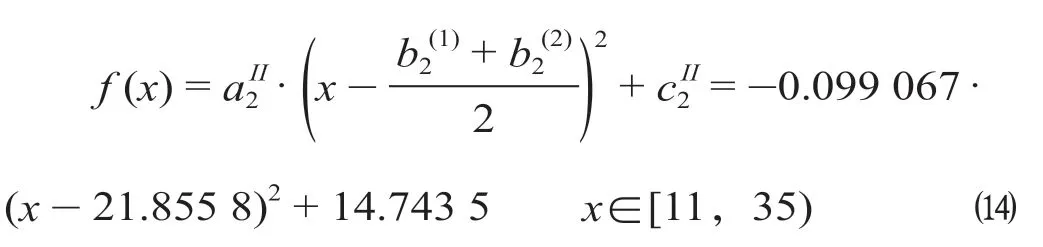
（3）第三次重联决策判定。对于中午和下午发车的车次，可以进行第三次重联决策判定。当预售时间进入开车前第3 h，即t- 8 h 内，可以根据第4 ～ 11 h 的售票数据对第一段进行拟合，并根据第11 ～ 35 h 的售票数据对第二段重新进行拟合，得到参数据此进行第三次判定。由于第二次判定时，第三段拟合已使用到第三段全部数据，故在第三次拟合时不再重新拟合，参数开车前11 ～ 35 h 分小时售票数据如表3 所示。开车前4～11 h 分小时售票数据如表4 所示。

根据公式2 所示分布及其系数取值范围，拟合得到第二段的购票－时间函数为

表2 开车前25 ～ 49 h 分小时售票数据Tab.2 Hourly tickets pre-selling volume within 25 to 49 hours before departures

表3 开车前11 ～ 35 h 分小时售票数据Tab.3 Hourly ticket spre-selling volume within 11 to 35 hours before departures

表4 开车前4 ～ 11 h 分小时售票数据Tab.4 Hourly tickets pre-selling volume within 4 to 11 hours before departures

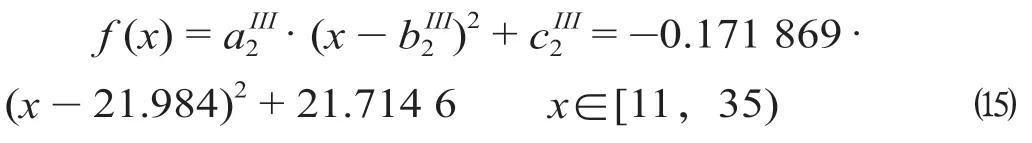
对第二次判定时的拟合参数进行修正，进而得到修正后的第二段的购票需求为修正拟合相对误差=1.24%。

令f(x) =f(11) = 0，根据公式2 所示分布及其系数取值范围，拟合得到第一段购票－时间函数为进而得到第一段的购票需求272.313 7，拟合相对误差进而计算拟合购票需求与单组参考需求Y(1)在第一、二、三段的接近程度= -0.055 3 < 0.5，由此得到第三次判定结果为单组。当时间进行到开车后，可以计算决策准确度值aIII=以直观地衡量第三次决策效果。开车前4 ～ 49 h 的拟合图像如图2 所示。

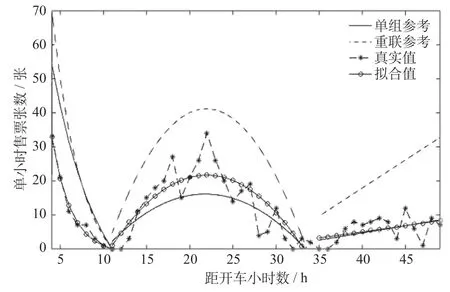
图2 开车前4 ～ 49 h 分小时售票数据拟合图Fig.2 Fitting graph of hourly tickets pre-selling volume within 4 to 49 hours before departures

同样，对2019 年4 月6 日(清明第三天)进行三次判定，得到判定结果与准确度值为：第一次判定结果为单组，决策准确度值为1.033 1；第二次判定结果为重联，决策准确度值为0.067 5；第三次判定结果为重联，决策准确度值为0.295 3。对2年清明节第三天的三次判定进行分别比较分析，可以看出此方法的准确性较好，除2019 年4 月6日第一次判定以外，决策准确度值均在0.5 以下。

南昌局集团公司采用该方法进行试验时，客票系统相应进行了调整。在30 d 开始预售车票时，仅销售一组动车组列车的车票，待到开车前两天内进行重联决策，如果决定重联，则放开销售另一组动车组列车的车票，既保证了市场需求的满足度，同时也尽可能的降低了运营成本。

3 研究结论

（1）针对“一日一图”目标下动车组列车开行方案决策过程中，较为关键的动车组列车重联决策问题进行研究，分析管内动车组列车的旅客购票规律，基于管内动车组列车购票特点，构建购票拟合需求模型。

（2）基于购票拟合需求模型，建立基于部分时段已售数据的重联决策判定方法，有助于铁路“一日一图”决策判定，精准优化动车组列车重联开行方案，实现铁路编组精细化管理，达到规范、经济、高效的管理目标。

（3）基于动态购票需求的铁路动车组重联决策实际过程中的干扰因素过于复杂，存在售票策略和列车售票组织之间的相互影响等，模型还应进一步全面考虑影响因素进行完善。