铁路列车晚点时间预测方法研究

2020-07-30彭其渊郭一唯

铁道运输与经济 2020年7期

石晶，彭其渊，文超，郭一唯，刘岭

（1.北京全路通信信号研究设计院集团有限公司信号院，北京 100073；2.西南交通大学交通运输与物流学院，四川成都 610031；3.西南交通大学综合交通运输国家地方联合工程实验室，四川成都610031；4.中国铁道科学研究院集团有限公司运输及经济研究所，北京 100081)

0 引言

列车晚点是列车运行中由于受到干扰而发生的实际运行线偏离图定运行线的现象。正常的列车运行秩序会因为列车晚点而受到扰乱，铁路运输产品的质量降低，影响旅客出行计划安排，也不利于行车安全。由于列车运行线间的关联性，列车晚点往往会向后传播，干扰后续列车的准点运行[1]。为此，列车调度员需要根据列车运行位置、速度及与前后车的距离，实时调整列车运行图，以控制和减小晚点传播的影响[2]。列车晚点预测可以为调度员提供列车运行调整的依据，以节省旅客的等待时间，优化旅客出行体验，提升综合交通网络总体运能和服务质量，对自动化调度指挥系统的实现和多方式交通方式协同发展至关重要。

国内外关于列车晚点预测的研究方法可以分为2 种。一种是假设晚点分布，基于列车运行冲突的机理和晚点传播理论，运用计算机模拟等方法研究列车晚点相关问题[3-4]；另一种是基于列车运行实绩数据，分析晚点概率分布及影响[5-10]，并将模糊Petri 网络模型[7]、神经网络模型[8]、基于马尔科夫链的模型及数据驱动方法[9]用于列车晚点预测。随着神经网络算法的发展和列车运行数据量增长，基于神经网络的列车运行晚点时间预测可以提高晚点时间预测的准确性，但基于实绩数据的多层神经网络模型训练过程复杂、体量庞大，推算实时列车晚点时间耗时相对较长，而基于实绩数据的逻辑回归模型在计算速度上表现更优。为此，结合铁路列车实绩晚点分布情况，选取广义线性模型对晚点时间预测问题进行研究。

1 铁路列车晚点预测方法

最初的列车晚点由列车运行过程中受到的干扰产生。由于车辆故障、线路故障、异物侵入等干扰因素引起的列车晚点称为初始晚点，由于晚点传播导致的列车晚点称为连带晚点。干扰具有传播特性，某一列车的干扰会影响其他列车的运行。列车运行晚点传播按方向可分为横向晚点传播和纵向晚点传播2 种。列车受到干扰后偏离图定时刻，如果其后方列车也受到干扰(即由一列车传播给多列车的干扰)称为横向晚点传播；若某一列车在某一车站或区间不能按图行车，干扰影响延伸至前方车站或区间，称为纵向晚点传播。干扰具有累积效应，随着干扰的数量和时间的增加，列车受影响程度增大。列车实绩运行数据是干扰累积、调度决策和列车运行状态共同导致的结果。由于列车运行干扰的随机性，仅分析单一干扰的影响不能充分反映实际情况。因此，基于列车运行实绩数据，分析挖掘列车运行晚点时间的预测方法是较为直接有效的方法之一。

1.1 列车晚点时间被动关系网

假定列车在区间运行采用准移动自动闭塞方式，采用目标距离控制模式，根据目标距离、目标速度及列车性能确定列车制动曲线。准移动闭塞的追踪目标点是前行列车所占用闭塞分区的始端。为保证前后2 列车安全运行，存在追踪间隔时间的限制，以保证车站办理2 列车到达、出发或通过作业安全。为此，车站前后行列车到达晚点时间和出发晚点时间之间存在制约关系。

列车运行晚点时间被动关系网如图1所示。图1中共有q个车站，通过因子间的被动关系形成关系网络。将i- 1 站出发晚点时间DDi-1、i站前行列车到达晚点时间LADi、出发晚点时间LDDi看作i站列车到达晚点时间主要干扰因素，如图1 中的红色箭头所示；将i站到达晚点时间ADi、前行列车i站出发晚点时间LDDi、i+ 1 站到达晚点时间LADi+1看作i站列车出发晚点时间主要干扰因素，如图1 中的黑色箭头所示。

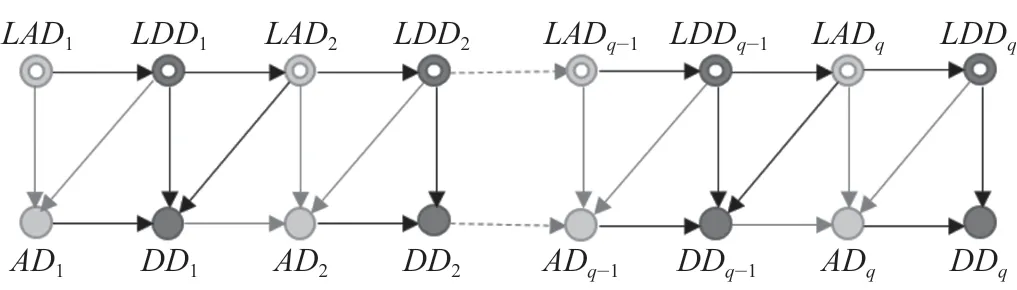
图1 列车运行晚点时间被动关系网Fig.1 Passive relation network of train delay time

1.2 列车晚点时间分布特征

以武广高速铁路(武汉—广州南)列车运行数据为例，武广高速铁路长沙南—广州北区段共有11 个车站，列车运行实绩数据采集于CTC 系统，包含途经各车站列车的图定及实际到发时刻，可得到对应的到发晚点时间。由于车辆故障、线路故障、异物侵入等干扰因素导致的列车晚点[11]称为初始晚点，具有较强的随机性和不可预测性。因此，对原始数据进行预处理，剔除因初始干扰造成的初始晚点，剩余的数据是列车连带晚点的数据。到达晚点时间频数分布如图2 所示，出发晚点时间频数分布如图3 所示

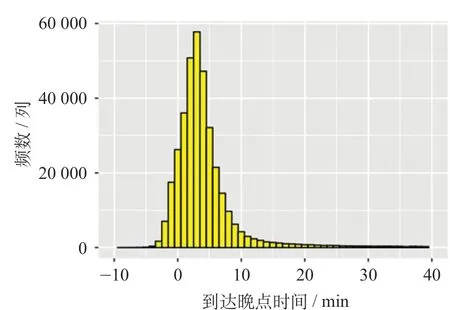
图2 到达晚点时间频数分布图Fig.2 Arrival delay time distribution

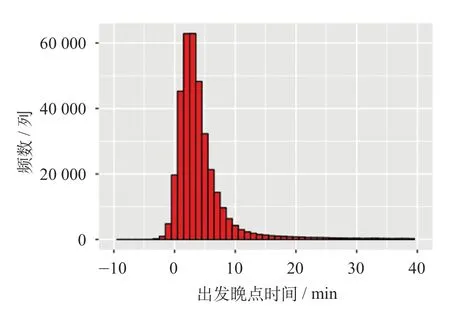
图3 出发晚点时间频数分布图Fig.3 Departure delay time distribution

由图2、图3 可知，列车晚点呈现明显的正偏态分布，大部分晚点时间集中于10 min 之内。在连带晚点的中，大晚点时间是影响旅客出行方式选择、运输方式衔接以及列车运行调度的重点，因此不能忽略大晚点时间因列车晚点传播等因素对相关列车运行的影响。采用上述数据，作为列车传播晚点时间预测的数据。

1.3 回归模型预测方法

由于晚点时间具有偏态分布的特性，为了保证大晚点预测的精确度，不宜采用基于概率的模型，而广义回归模型不需要关于变量分布的假设条件，包含非正态因变量的分析，拓展线性模型的框架，比较适合用于大晚点预测，为此选用广义回归模型作为预选模型。

对因变量Y和预测变量X1，X2，…，Xp间的关系进行建模。广义回归模型的拟合公式为

式中：g(μY)为条件均值函数；g为连接函数；μY为变量Y的条件均值；βj为未知参数。

设定连接函数和概率分布后，可以通过极大似然估计的多次迭代推导出各参数值。广义回归模型中，如果将连接函数设为logit 函数，可以得到Logistic 回归模型，如果将连接函数设置为log 函数，可以得到Poisson 回归模型。

依据《课程标准》，职业技术师范院校应在教师教育课程设置上体现育人为本、实践取向和终身学习的基本理念，体现教育信念与责任、教育知识与能力、教育实践与体验这三个总体目标，满足课程最低必修学分10学分、最低总学分14学分、最低教育实践时间18周的要求，加强教育实践环节，提升教育实践课程的管理水平和质量，大力推进课程改革，创新教师培养模式，探索合作培养师范生的新机制。

（1）Logistic 回归模型。列车到达晚点时间作为因变量，可采用多分类Logistic 回归用于列车到达晚点时间模型的建立，利用对数最大似然函数法求解多分类Logistic 回归模型。记因变量y有n个取值，取值范围为[0，n- 1]，自变量Z有c类，Z= (z1，z2，…，zc)，那么y的条件概率为

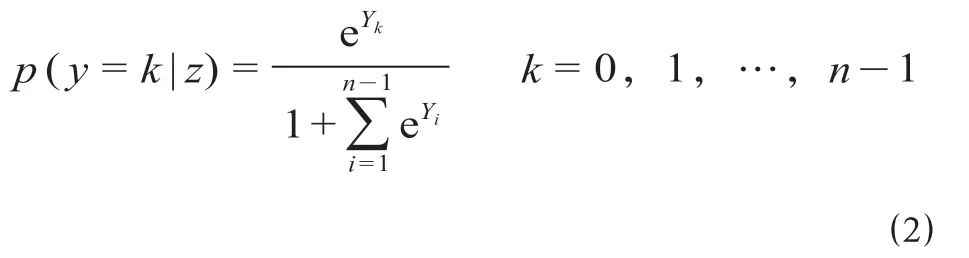
式中：p(y=k|z)表示y视作z类别标记为k的可能性。

相应Logistic 回归模型的表达式为

式中：Yk为条件均值函数；β1,k，β2,k，…，βc,k为偏回归系数。

（2）Poisson 回归模型。Poisson 回归模型通过一系列连续型或类别型预测变量，预测计数型结果变量的有效工具。假设计数随机变量Yi，其中i=1，2，…，n服从均值为λi的Poisson 分布，那么Yi的概率密度函数为

式中：P(Yi=yi)为n个独立实验中，该事件发生yi次的概率分布；λiyi为某事件总体的发生次数。

其对数似然函数方程为

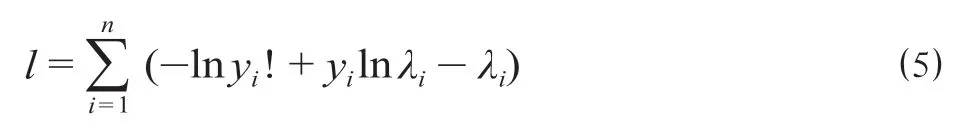
将列车运行数据分为训练集和测试集，运用训练集训练模型，测试集测试预测精度。在上述回归模型中，确定较优的列车晚点时间预测方法，比较分析预测精度和晚点分布。

2 相邻列车晚点预测建模

2.1 变量说明

从列车实绩数据中可以提取晚点时间、区间运行时间、运行速度、间隔时间、停站时间、缓冲时间等因子，采用向后选择法，构建回归模型，根据F 统计量的P值确定哪个自变量对因变量有显著影响。结果显示，相关联晚点时间对因变量具有显著影响。因此，结合列车运行晚点时间相关关系，确定DDi-1，LADi，LDDi作为指定列车到达晚点时间ADi的预测因子；将ADi，LDDi，LADi+1作为指定列车出发晚点时间DDi的预测因子。经过数据初步处理，剩余列车到达晚点时间预测模型建模数据量59.91 万，列车出发晚点时间预测模型建模数据量58.09 万，相邻到发晚点预测模型变量说明如表1 所示。

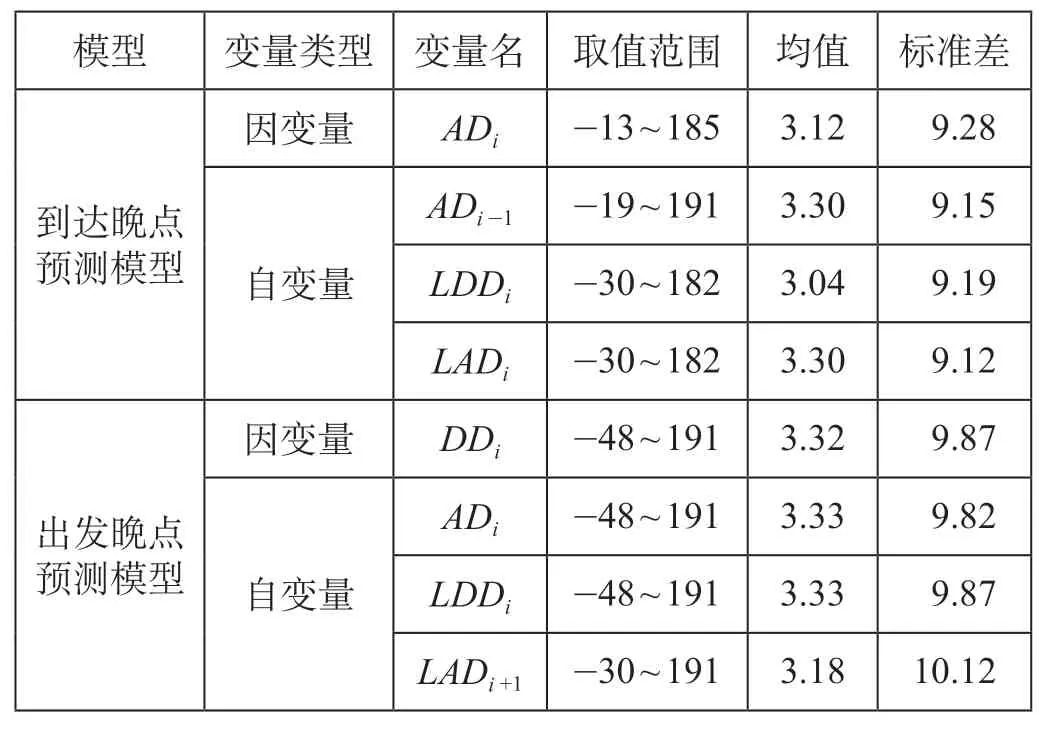
表1 相邻到发晚点预测模型变量说明 minTab.1 Adjacent to the arrival and departure delay time prediction model of variable description

2.2 数据预处理

2.2.1 多重共线性检测

预测因子间的线性相关性会影响回归模型的参数估计并使得模型失真，需要通过构建多元线性规划模型，并对预测因子做多重共线性检验，检验数据是否能够达到构建回归模型要求。晚点时间预测模型自变量的膨胀因子如表2 所示。表明存在多重共线性问题。由表2 可知，2 个模型的VIF值均有表明模型存在多重共线性问题，不能通过多重共线性检测。因此，在构建预测模型之前，需要将预测因子进行主成分分析，通过降维的技术，将几个预测因子化为少数主成分，消除因子间的高相关性。

表2 晚点时间预测模型自变量的膨胀因子Tab.2 VIF of independent variables in delay time prediction model

2.2.2 主成分分析

使用R 语言CARET 包中PREPROCESS 函数，采用因子标准化和主成分分析方法，消除因子的高相关性。晚点预测模型因子方差贡献率如表3 所示。

表3 晚点预测模型因子方差贡献率 %Tab.3 Factor variance contribution rate of delay time prediction model

由表3 可知，保留PC1 和PC2 主成分，能够达到累计方差贡献率达到95%的要求，即能够最大程度上保留因子的特征，因而保留主成分PC1和PC2 作为预测模型因子。

2.3 预测模型比选

将建模数据中的70%作为训练集，30%作为测试集。采用K 折交叉验证方法(k= 5)，使用预测模型精度、模型参数、真实值与预测值分布比较作为验证指标。使用了R 语言中GLM 函数构建广义回归模型，预测列车晚点时间。以PC1，PC2为自变量，分别对到达晚点预测模型(因变量ADi)和出发晚点预测模型(因变量DDi)构建Logistic 回归和Poisson 回归模型。模型均可以通过显著性检验(t 检验)。不同允许误差下模型预测精度比较结果如表4 所示。由表4 可知，采用Logistic 回归模型作为相邻到发晚点时间预测模型预测效果更优。

表4 不同允许误差下模型预测精度比较结果Tab.4 Comparison of model prediction accuracy under different allowable errors

模型预测精度评估参数结果如表5所示。由表5可知，模型的MAE、RMSE值较小，拟合优度分别为0.96 和0.99，说明模型能够充分说明解释模型变量并较准确预测列车晚点时间大小。

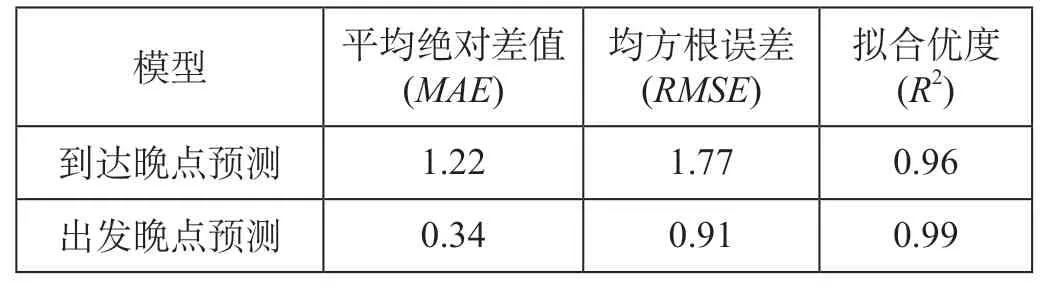
表5 模型预测精度评估参数结果Tab.5 Model parameter results

2.4 预测结果分析

由于列车晚点时间具有明显正偏态分布的特性，且晚点时间具有跨度范围大、标准偏差较大等特征，因而比较分析预测值与真实值。到达晚点时间模型和出发晚点时间模型的预测值和真实值变化趋势图如图4 和图5 所示。由图4 和图5 可知，预测值与真实值大小、范围和变化趋势符合较好，预测效果较好。

3 相间列车晚点预测建模

根据列车运行关系和相邻晚点时间预测结果，确定预测j站某列车到达晚点时间ADj和出发晚点时间DDj的预测因子为i站到达晚点时间ADi、前行列车i站出发晚点时间LDDi，i+ 1 站到达晚点时间LADi+1，i站出发晚点预测时间p_DDi。模型变量说明如表6 所示。其中，相间车站的数量为w(w= 1，2，…，5)，有w=j-i。

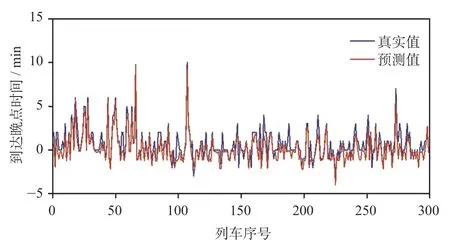
图4 到达晚点时间预测模型预测结果Fig.4 Prediction results of arrival delay time prediction model

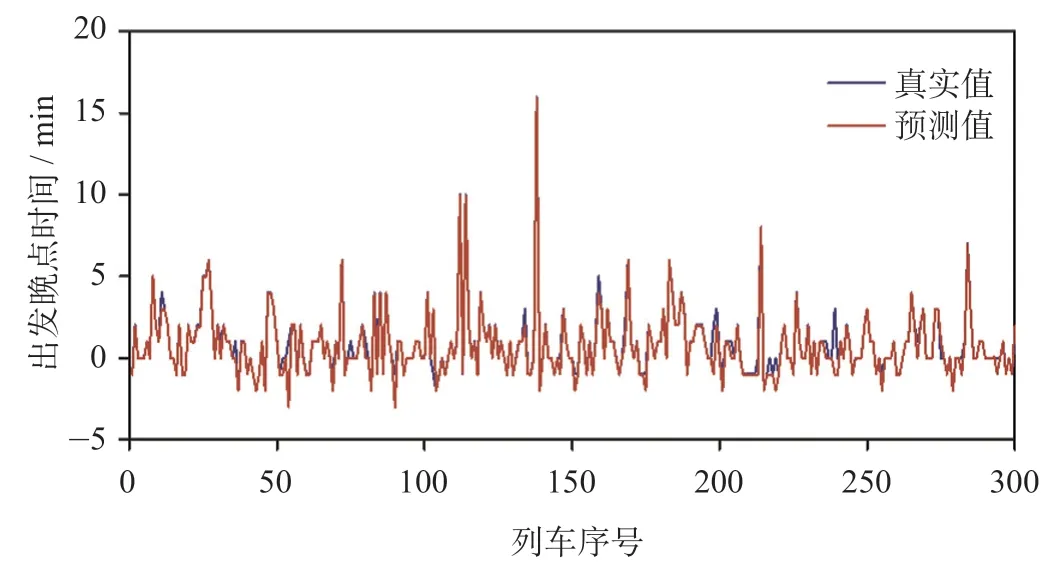
图5 出发晚点时间预测模型预测结果Fig.5 Prediction results of departure delay time prediction model

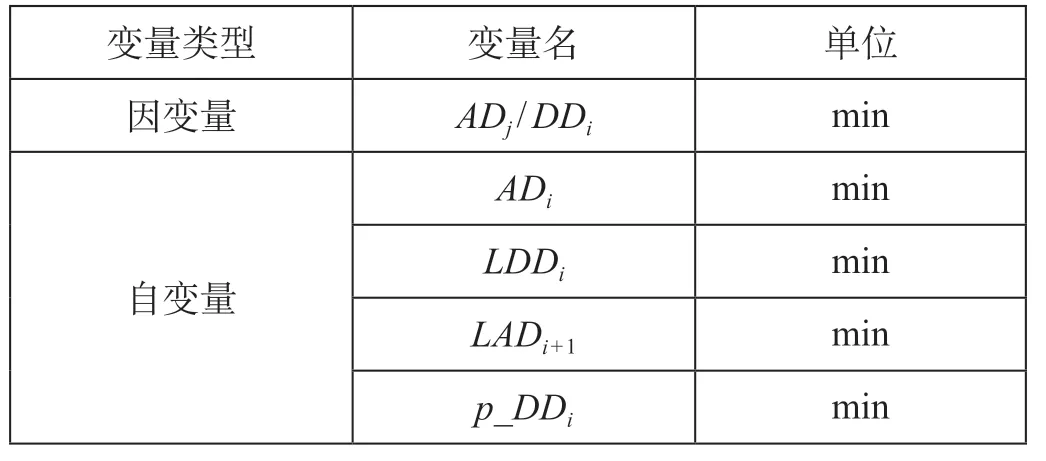
表6 模型变量说明Tab.6 Model variable description

由于采集数据量限制，预测晚点时间相间车站w不同，对应的有效建模数据量不同。模型有效数据量如表7 所示。

相间到发晚点预测模型建模数据初步处理和预处理过程与相邻到发晚点预测建模过程相同。根据模型预测精度比选和预测结果，结合真实值对比分布、变化趋势等，确定Logistic 回归模型为相间到发晚点预测模型的最优模型。相间站点数量w对应的相间到达晚点时间预测精度如下图6 所示；相间出发晚点时间预测精度图7 所示。

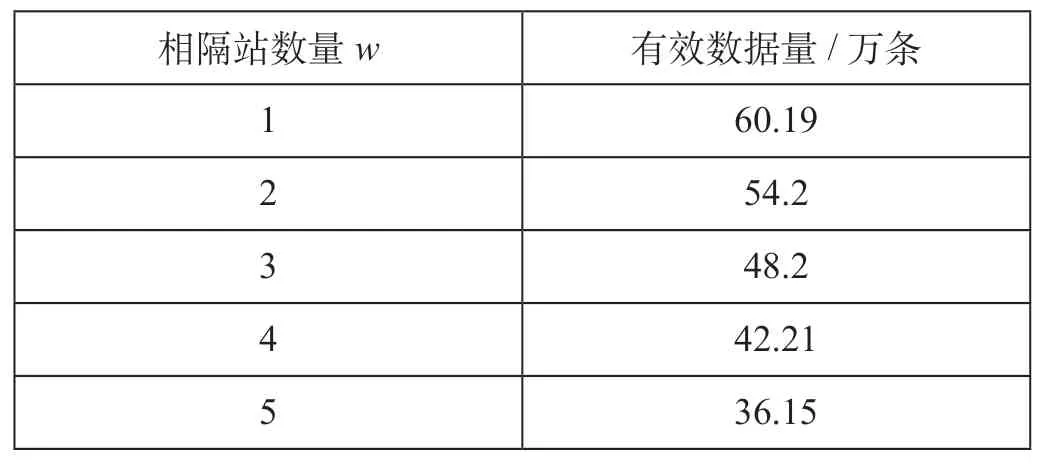
表7 模型有效数据量Tab.7 Number of valid data for the model

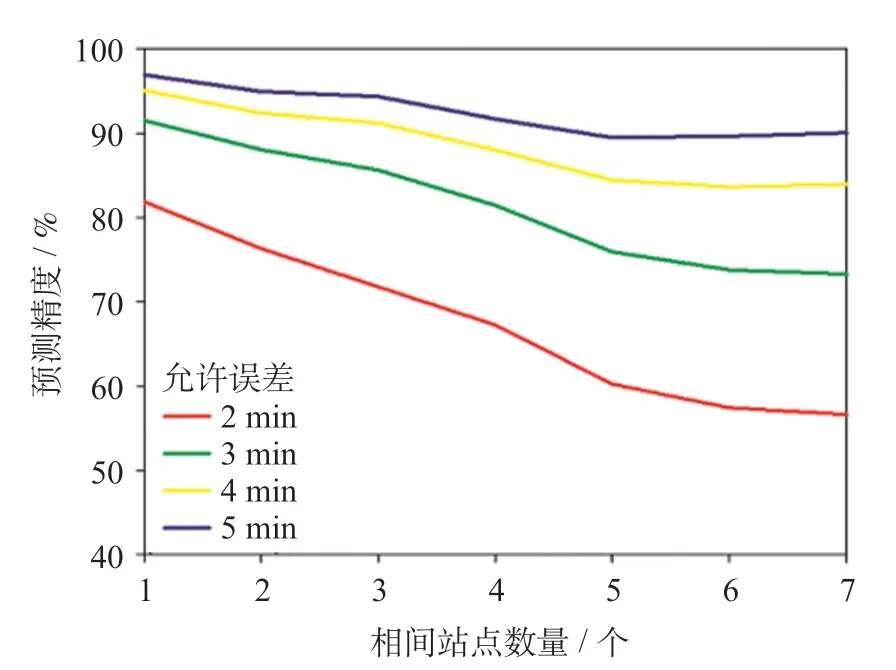
图6 相间到达晚点时间预测结果Fig.6 Prediction result of arrival delay time of following train

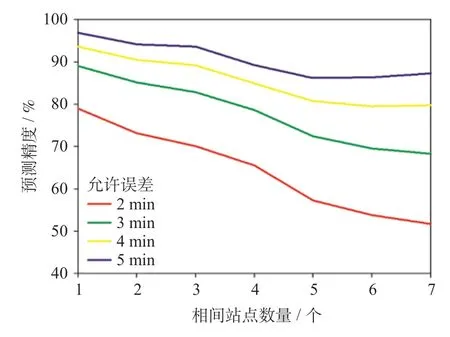
图7 相间出发晚点时间预测结果Fig.7 Prediction result of departure delay time of following train

由图6 和图7 可知，随着预测相隔站点数量逐渐增加，预测精度随之降低。当w= 4 时，在2 min 允许误差下，预测精度为67.26%；在3 min允许误差下，预测精度80%以上；仅通过列车运行关系和晚点时间传播规律预测较远车站晚点时间精度有待提高，但是可以通过不断修正预测因子数值，以提高预测精度。因此，此方法具有粗预测性、易修正性和快速响应性，可以作为旅客行程规划及乘务组织的预警及参考。