基于空中交通密度的进场航班动态协同排序方法
2020-07-30刘继新江灏董欣放兰思洁王浩哲
刘继新,江灏,*,董欣放,兰思洁,王浩哲
1. 南京航空航天大学 民航学院,南京 211106 2. 国家空管飞行流量管理技术重点实验室,南京 211106 3. 中国民用航空华北地区空中交通管理局天津分局,天津 300300
近年来,在全球经济稳步复苏,中国经济运行稳中向好的态势下,民航主要运输指标保持平稳较快增长。2018年,民航全行业完成运输总周转量1 206.53亿吨公里,比上年增长11.4%;全行业运输航空公司完成运输起飞架次469.47万架次,比上年增长7.6%。以上数据表明,中国航空事业正快速发展,这使得航班数量日益增加,也增加了保障航班正常运行的压力;同年全国客运航空公司共执行航班434.58万班次,平均航班不正常率为19.87%,平均航班延误时间为15 min[1]。
航班运行是严格基于管制员指令的,航班落地的时间依赖于管制员为其分配的次序。目前对进场航班的排序主要由管制员在熟悉各类航空器性能的基础上,依据航班的动态信息与飞行计划,依靠经验进行。这种方法在任务繁重时,管制员的工作负荷较大、空管系统运行效率较低,且会导致大量的航班延误。因此,空管部门希望在保证航班安全的前提下,尽量降低管制员的工作负荷。同时,航空公司和机场也基于自身利益,对进场航班排序提出了各自的要求:机场部门希望机场资源最大化的转化为经济效益并提高航班正常率;航空公司希望在保证市场公平性的前提下使得本公司的航班延误最小。这样,航班排序问题就变成多种因素耦合,复杂度急剧增高,先到先服务(First Come First Served, FCFS)的排序方法已经不能够满足航班排序的需要,这就需要使用更加科学合理的航班调度方法以满足空管、航空公司和机场的诉求。
国内外相关学者从不同的角度对航班排序问题开展了大量研究,航班排序问题的研究主要集中于:动态调度、多跑道/多机场协同等。模型方面,文献[2]基于滚动时域控制(Receding Horizon Control, RHC),将静态调度推广到动态调度领域。在RHC框架下,文献[3-4]求解了多跑道机场的进场动态调度问题;文献[5]建立了航班动态排序模型;文献[6-8]从跑道协同的角度,实现进离场航班动态协同优化排序。文献[9-10]引入多元受限时间窗的创新理念和航班满意度概念,建立了多机场终端区进离场交通流协同排序模型。文献[11-12]引入外围航班流概念,建立了多机场终端区进离场航班协同优化排序模型。算法方面,遗传算法[3-5,9-10]、分支定界法[6-8]、模拟退火算法[11-13]、蚁群算法[14]、贪心算法[15-16]、分散搜索算法和生态算法[17]等均被用来解决进场航班排序问题。目前国内外对于进场排序的研究成果较为丰富,部分已经应用于实际运行,如欧洲的进场管理(Arrival MANagement, AMAN)系统。但在下列研究领域中,仍有需要提升的空间:① 在实际运行过程,如何根据不同时段空中交通密度情况调整资源,选择合理的优化目标与排序方案,在当前研究中尚有欠缺;② 在未来航空运输业多方协同决策的发展趋势下,当前研究未充分考虑空管、航空公司和机场对于进场航班排序的协同决策因素。
本文立足于民航运输业多方协同决策的发展趋势,以单跑道机场为对象,重点研究了不同空中交通密度下进场航班动态协同排序问题。研究工作着眼于进场航班排序的“动态性”和“协同性”。在满足进场航班排序的“动态性”方面,基于进场航班的广播式自动相关监视系统(ADS-B)数据,设计一种进场航班动态排序方法。本文的“协同性”是指在对进场航班排序时,充分考虑空管、航空公司和机场的诉求。这些将在以下内容中进行详细阐述。
1 进场航班动态排序方法
为了满足对进场航班排序的实时性和动态性要求,常用的策略是RHC,即每间隔一段时间对进场航班进行排序,从而实现对进场航班的连续排序过程。由于民航运输业拥有大量可以获得的运行数据,如雷达数据、ADS-B数据等,因此本文结合民航运输业的运行特点,利用进场航班ADS-B数据中的航班号和航班实时位置信息,结合进场航班飞行计划数据,设置相应的进场航班排序触发及更新规则,作为实现航班实时、动态和自动化排序的基础。
1.1 进场航班排序触发及更新规则
进近管制区是连接区域管制区和机场塔台管制区之间的空间。在实际运行中,对进场航班排序由进近管制员完成,进近管制员对进入进近管制区的进场航班进行排序,并通过调速、引导等手段实现预定次序。
本文模拟实际运行过程,设置以机场基准点为圆心的2个同心圆:起始圈和更新圈(如图1所示),将更新圈内的范围模拟成进近雷达管制区,起始圈和更新圈之间的范围作为航班排序的缓冲区域,以使得进场航班在进入进近雷达管制区前即获得落地次序,以便进近雷达管制员有充分的时间和充足的空间实现预定次序。起始圈和更新圈的构型亦可根据管制区的实际边界形状来确定。

图1 进场航班排序触发及更新规则Fig.1 Rules for triggering and updating arrival flight sequencing
基于以上设置的进场航班排序起始圈和更新圈,结合ADS-B数据,设置一种进场航班排序触发及更新规则:在当前排序阶段,当第1架进场航班到达更新圈即触发起始圈与更新圈之间的进场航班排序;以下一排序阶段第1架进场航班到达更新圈作为排序更新触发条件,对下一排序阶段的进场航班进行新一轮排序从而实现对所有进场航班的连续排序。
1.2 起始圈和更新圈半径的确定
1) 更新圈半径R1
进近管制空域的水平范围通常为半径50 km或者走廊进出口以内的除机场塔台管制区以外的空间[18]。因此,本文将更新圈的半径R1设置为50 km。
2) 起始圈半径R2
考虑到进近管制员应当有充足的空间和时间对各进场航班实施相应的管制方法,从而按照预定次序完成对进场航班的排序工作,故对进场航班落地次序的确定应当尽早完成。借鉴RHC中的排序时间窗概念,本文取15 min时间窗对应的航班飞行距离作为缓冲区域的长度。进场航班在接近进近管制区时的速度约为600 km/h,由此得到的缓冲区域长度为150 km,故将起始圈的半径R2设置为200 km。
1.3 进场航班动态排序方法流程
本文提出的进场航班动态排序方法流程如图2 所示。

图2 进场航班动态排序方法Fig.2 Dynamic sequencing method for arrival flights
步骤1将实时接收到的ADS-B数据(Data1)和本场进场航班飞行计划(FP1)相关,筛选出本场进场航班的ADS-B数据(Data2)。
步骤2根据Data2中的航班位置信息,判断是否满足1.1节提出的进场航班排序触发及更新规则,若满足,则进行步骤3;若不满足,则返回步骤1。
步骤3进一步处理Data2,筛选出此刻处于起始圈和更新圈之间的进场航班ADS-B数据(Data3),并从FP1中提取出Data3中涉及到的航班的飞行计划数据(FP2)。输出Data3和FP2作为后续对航班排序的初始输入信息,并将FP2从FP1中删除以完成对FP1的更新。
步骤4排序阶段加1,返回步骤1。
2 模型建立
在CDM理念下对进场航班排序时,希望考虑到空管、航空公司和机场的诉求,但各方的目标众多且一致性不强,甚至各目标之间会相互冲突,因此造成多目标进场航班排序问题的高复杂性。针对这一问题,本文以单跑道机场为例进行建模,提出一种基于空中交通密度的进场航班协同排序模型,从而满足各方的定制化需求。
假设F为某日所有进场航班的集合;Fi为第i个排序阶段的所有进场航班的集合。
2.1 目标函数
1) 跑道容量最大
本文考虑的最大化跑道容量,即某排序的最后一个进场航班的落地时间最小:
(1)
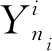
2) 航班延误均衡性最高
本文综合考虑航班总体延误时间和个体延误时间,提出航班延误均衡性概念。本文将航班偏离计划时刻当作延误处理,则某排序阶段内的航班延误均衡性最高,即
(2)
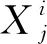
3) 航班正常率最高
对进场航空器而言,航班正常判定标准为:不晚于计划开舱门时间后10 min落地[19]。某排序阶段内的所有进场航班正常率最高,即
maxWi
(3)
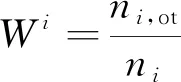
4) 航班延误公平性最高
本文将航班延误公平性以进场航班延误时间均值和标准差来反映,因此某排序阶段的进场航班延误公平性最高,即进场航班延误时间均值和标准差最小:
minAi
(4)
minσi
(5)
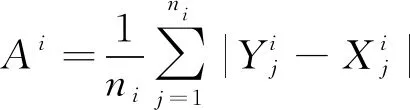
2.2 约束条件
本文提出的基于空中交通密度的进场航班协同排序模型,在管制间隔要求的基础上,将其他运行约束与限制均转化为时间窗约束。模型中涉及的约束条件如下。
2.2.1 管制间隔要求
由于进近管制员连续移交给塔台管制员的进场航班高度通常为某一双方约定的协议高度,故对于进场航班而言,其必须满足水平间隔要求。当前进近管制单位多采用雷达管制,其中运行的进场航班在进近-塔台移交点处受到的水平间隔约束有:雷达尾流间隔、雷达管制间隔和协议间隔。塔台管制是有雷达设备的程序管制,塔台管制下的进场航班落地前受到的水平间隔约束主要为非雷达间隔的尾流间隔。
1) 雷达尾流间隔
航空器在飞行过程中由于机翼上下表面的压力差,会在翼尖处产生涡流,对后续飞行航空器的安全造成影响。因此,航班进场序列必须满足尾流间隔要求,即
(6)

2) 雷达管制间隔
航班进场序列必须满足雷达管制间隔要求,即
(7)

3) 协议间隔
航班进场序列必须满足进近-塔台移交的协议间隔要求,即
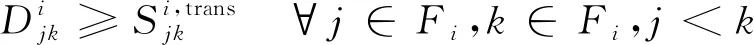
(8)

综上,航班进场序列在进近-塔台移交点处必须满足管制间隔要求,即
(9)
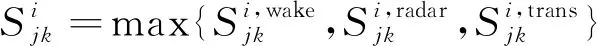
4) 非雷达间隔的尾流间隔
前后进近着陆的航班应能满足非雷达间隔的尾流间隔要求,即
(10)

2.2.2 时间窗约束
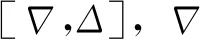
1) 可行着陆时间窗
终端空域范围有限,考虑到航空器性能、燃油储备、进场航线等因素的限制,为保证优化序列的可行性,优化序列中进场航班的计划落地时间必须处于航班的可行着陆时间窗[E,L]内。
(11)
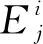
2) 可接受延误时间窗
在管制运行过程中,管制员会根据不同类型进场航班的重要度,在进场排序时考虑其优先级。本文在文献[9]的基础上,建立进场航班类型和其可接受的最大提前/推迟到达时间之间的关系,从而得到进场航班可接受的延误时间窗。

(12)

3) 管制负荷限制时间窗
管制员对于优化序列中与FCFS序列中次序偏差较大的航班,需要对其发布大量的附加指令,这会增加管制员的工作负荷。最大约束位置转换(Maximum Position Shift, MPS)规定了优化序列中各航班次序相对于FCFS序列中相应航班次序的最大偏移量。由于航班次序的偏移也即航班到达时刻的偏移,因此,可以建立MPS约束和航班计划落地时间之间的关系。基于以上分析,本文将MPS约束转化为一种时间窗约束——管制负荷限制时间窗。
(13)
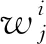
4) 公平性约束时间窗

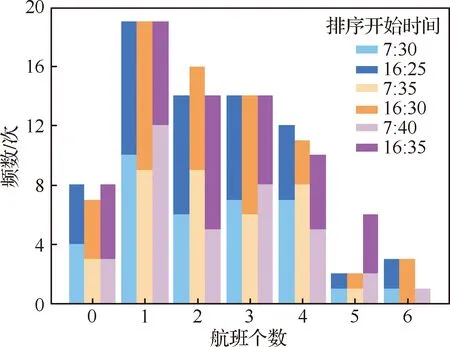
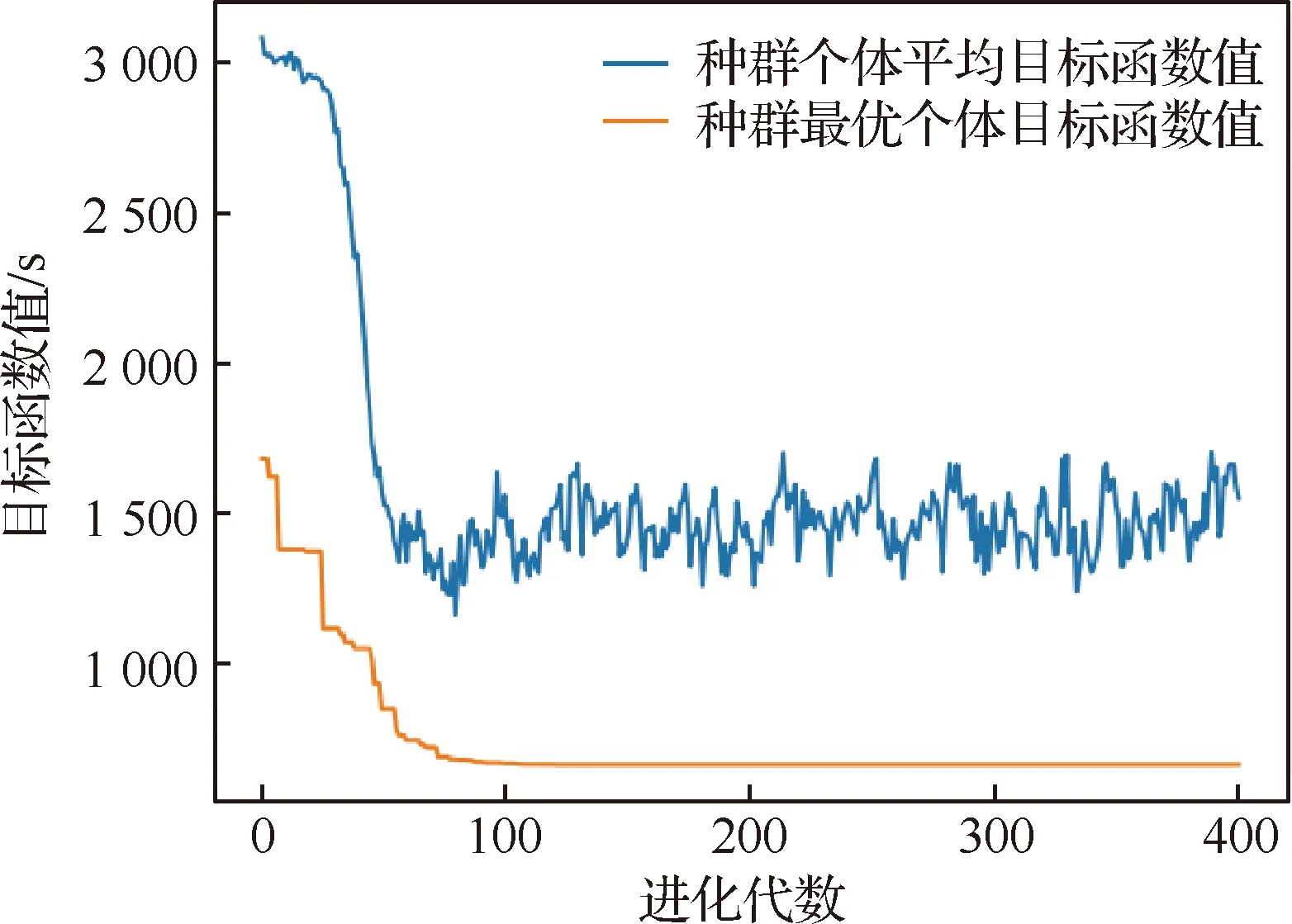
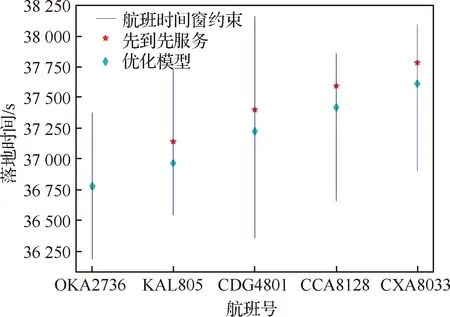
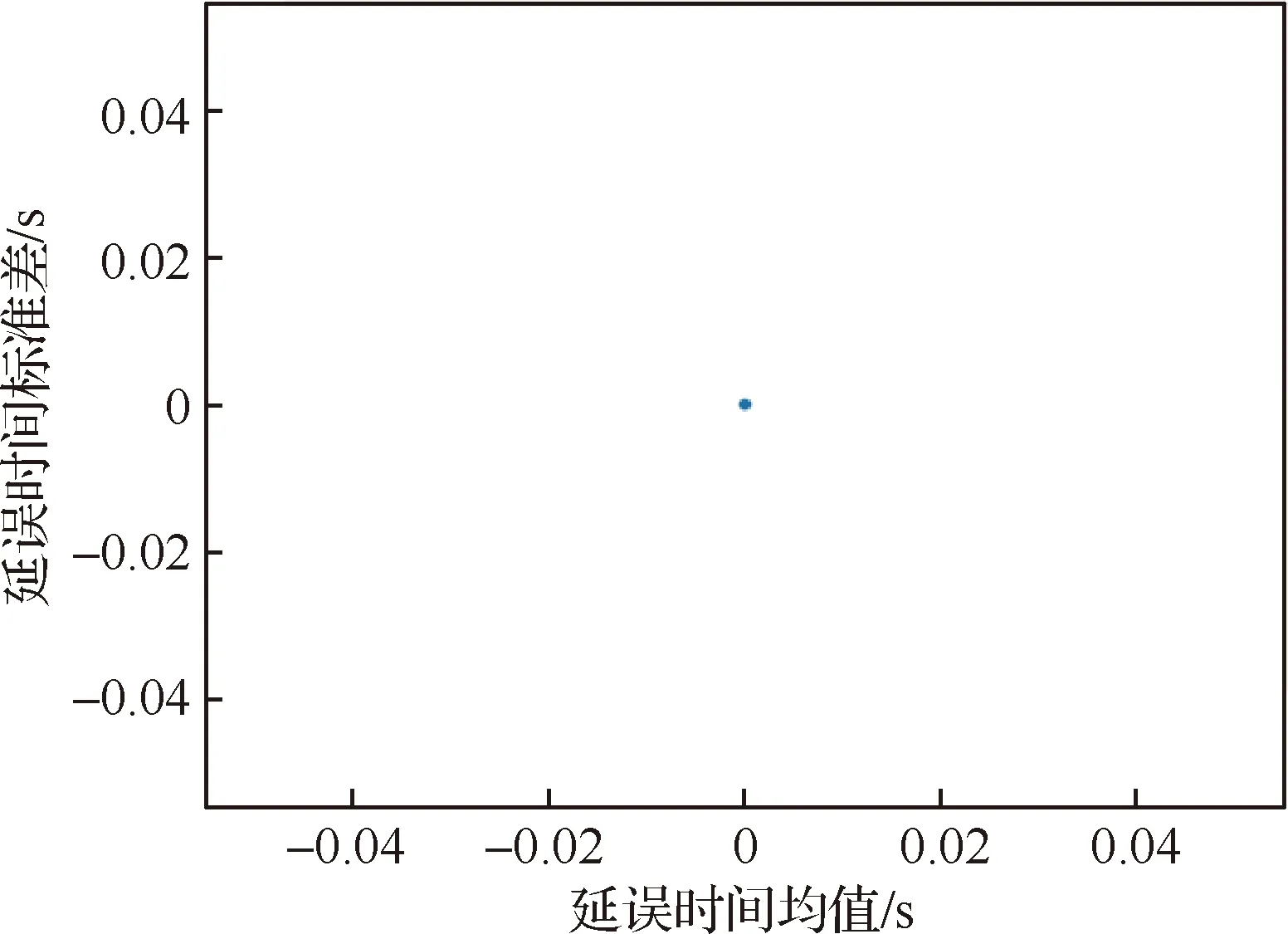
对于第i个排序阶段使用同一进场航线的第j和k个进场航班(j 图3 公平性约束时间窗调整Fig.3 Equity constraint time window adjustment 2.2.3 变量约束 目标函数及约束条件中涉及的各变量取值应满足如下的约束: i,j,k,ni,ni,ot,K∈N (14) j,k,ni,ot≤ni (15) (16) 在CDM的理念下,应当充分考虑管制单位以外的航空公司和机场对于进场航班排序的决策因素。因此,本文设计了一种时隙交换方法以提高航空公司在进场航班排序过程中的参与度。 在实际运行中,航空公司从商业角度出发,基于对本公司的商业利益等多方面综合考虑,对于航班的重要性分析与管制单位的分析存在差异。如:某个航班落地后有后续的飞行任务或者有较多落地机场换乘旅客,且前站已经延误,航空公司为减小延误损失,希望此航班尽快落地。时隙交换让此设想成为可能。 2.3.1 时隙交换规则 本文涉及的时隙交换是指:在对进场航班进行优化排序后,航空公司在满足航班可行着陆时间窗约束(式(11))的前提下,可对优化排序结果中分配给本公司航班的着陆次序进行再分配,牺牲本公司某个或某些进场航班的利益以优先保障重要进场航班,从而提高决策的科学性和合理性。 考虑到尾流间隔的不对称性,为使得交换时隙后不影响其他公司的航班,保证航空公司间的公平性,本文设计的时隙交换规则如下: 1) 同一航空公司同一尾流等级的进场航班之间。 或者 2) 在不影响其它航空公司航班时,同一航空公司不同尾流等级的进场航班之间。 2.3.2 时隙交换方法流程 基于本文2.3.1节设计的时隙交换规则,本文的时隙交换方法实施步骤如下: 步骤1根据实时排序结果和2.3.1节时隙交换规则,确定可进行时隙交换的航空公司及其对应的可发生时隙交换的航班。 步骤2向步骤1确定的各航空公司发送各自相应的可发生时隙交换的航班排序信息Seq1:航班号和初始落地次序。 步骤3各航空公司在收到Seq1后进行决策,向管制单位发送时隙交换后的航班排序信息Seq2。 步骤4将所有收到的Seq2进行整合并结合Seq1,获得最终的排序结果。 基于空中交通密度的进场航班协同排序模型根据当前排序阶段的空中交通密度高低,选择相应的目标函数和约束条件对进场航班进行排序。在对空中交通密度大小进行分类时,主要考虑当前排序阶段空中交通的拥挤程度,文献[20]对欧洲、美国及日本的扇区交通流拥挤判定方法进行了比较分析,本文选取欧洲中央流量管理单位(Central Flow Management Unit, CFMU)的扇区流量黄色告警,即交通流量超过容量C的80%,作为判定空中交通密度高的标准;对于判定空中交通密度低的标准,本文设定为交通流量低于容量的50%。 通过以上分析,建立基于空中交通密度的进场航班协同排序模型如下: 1) 高密度(ni≥80%C) 此时,空中交通密度高,减轻管制负荷和提升跑道容量是当前最关注的问题。此时同时考虑的是空管和机场的利益,为减轻管制负荷,使用MPS约束并规定使用同一进场航线的进场航班间不允许超越;以当前排序阶段内最后一个进场航班的计划落地时间最小为目标,从而最大化跑道容量。即目标函数为式(1),约束条件为式(9)~式(13)。 2) 中密度(80%C>ni≥50%C) 此时,空中交通密度适中,管制员开始有一定的调配空间和时间,管制负荷不再是主要关注点,将航空公司的利益考虑进来,以航班延误均衡性最高为目标。即目标函数为式(2),约束条件为式(9)~式(12)。 3) 低密度(ni<50%C) 此时,空中交通密度较低,管制员有充足的调配空间和时间,同时考虑航空公司和机场的诉求。从机场的角度出发,以航班正常率最高为目标;从航空公司角度,以航班延误公平性最高为目标,并引入时隙交换方法满足航空公司的定制化需求,从而实现三方协同排序。即目标函数为式(3)~式(5),约束条件为式(9)~式(12)。 进场航班动态协同排序问题具有多目标和多约束,属于典型的非确定性多项式难解(Non-deterministic Polynomial-Hard, NP-Hard)问题。而遗传算法作为经典的智能优化方法,其并不需要事先描述问题的全部特点及确定算法应采取的措施,由于其具有的此种健壮性,特别适合于处理传统搜索算法解决不好的复杂和非线性问题。因此,本文采用精英保留的遗传算法(EGA)[21]和带精英策略的快速非支配排序遗传算法(NSGA-II)分别对所建立的单目标和多目标模型进行求解。EGA和NSGA-II均使用了精英保留策略,此策略在种群进化过程中,保证了找到的最优解不会被抛弃,是群体收敛到优化问题最优解的一种基本保障。NSGA-II适用于求解复杂的多目标优化问题,其解决了NSGA的主要缺陷,具有快速、准确的搜索性能[22]。 所提算法的流程图如图4所示。 图4 所提算法流程图Fig.4 Flowchart of proposed algorithm 步骤1获得本场进场航班的飞行计划数据(FP1)和实时接收到的ADS-B数据(Data1)。 步骤2对FP1和Data1使用进场航班动态排序方法进行判断,以确定是否触发排序。若是,获得Data3和FP2,并完成对FP1的更新,进行步骤3;否则,返回步骤1。 步骤3根据Data3和FP2,运用基于空中交通密度的进场航班协同排序模型获得空中交通密度分类以及对进场航班排序的目标函数及约束;同时,此排序阶段数据处理完成,返回步骤1进行后续的数据判断及处理工作。 步骤4判断空中交通密度分类。若是低密度,使用NSGA-II进行排序计算,获得初步排序结果,时隙交换后获得最终排序结果;若是中/高密度,使用EGA进行排序计算,获得的排序结果即最终排序结果。 3.2.1 管制间隔处理 本文在对进场航班优化排序时综合考虑雷达尾流间隔、雷达管制间隔、协议间隔和非雷达间隔的尾流间隔,并将基于距离的间隔要求进行空间—时间转化,以获得进场航班落地时间间隔要求。 情形1前机慢后机快(如图5所示) 图5 情形1 (前机慢后机快)Fig.5 Situation 1(trailing aircraft is faster than leading one) 此时进场航班在进近到落地过程中,接地点处二者的相对距离最小。 (17) 情形2前机快后机慢(如图6所示) 图6 情形2(前机快后机慢)Fig.6 Situation 2 (leading aircraft is faster than trailing one) 此时进场航班在进近到落地过程中,进近-塔台移交点处二者的相对距离最小。 (18) 综上,进场航班的落地时间应当满足: (19) 3.2.2 时间窗处理 1)可接受的最大提前/推迟到达时间 本文考虑机场和航空公司双方的诉求,将机场基地航空公司航班的重要度设置为次高等级。 2) 单位时间偏移量 3.2.3 遗传算法编解码 本文在进行模型求解时将以时分形式表示的时间均转换成用秒表示,即将a时b分转换成秒的转换公式为:a×3 600+b×60。 本文采用实数编码的方式对进场航班的计划落地时间进行编码。根据2.2.2节确定的航班时间窗约束,第i个排序阶段第j个进场航班的计划落地时间编解码公式为 (20) 天津滨海国际机场(ZBTJ)拥有平行双跑道并采用隔离平行运行模式,其中仅有东跑道用于落地,其适用于本文提出的优化排序模型。因此,本文以天津滨海国际机场为例,对某日某时段的进场航班进行动态协同排序。 综合考虑算法运行时间和收敛效果,多次调整参数取值并进行仿真实验,获得对于进场航班排序问题有效的算法参数如下: 1) EGA控制参数包括:种群规模为100;最大进化代数为400;染色体编码长度为ni;采用两点交叉,交叉概率为1;采用实值变异,利用压缩率和梯度划分来控制变异距离,压缩率为0.5,梯度为20。 2) NSGA-II控制参数包括:种群规模为200;最大进化代数为500;染色体编码长度为ni;采用模拟二进制交叉和多项式变异,交叉和变异概率均为1,分布指数为20。 本文将基于RHC策略的动态排序方法(简称RHC方法)、基于先到先服务策略的排序方法(简称先到先服务方法)与所提的基于空中交通密度的进场航班动态协同排序方法(简称动态协同方法)进行对比,以评估所提方法的优化效果。本文选择某日2个不同时段,共对165架次(时段1∶82架次、时段2∶83架次)进场航班进行排序。 4.2.1 RHC方法与动态协同方法对比 本文设定RHC的排序时间窗为30 min,滑动时间窗为15 min。图7为RHC方法对时段1的不同排序开始时间(7∶30、7∶35和7∶40)和时段2的不同排序开始时间(16∶25、16∶30和16∶35),每次排序时涉及的航班个数及其在排序时段内出现的次数统计。由图7可见,RHC方法对于不同的排序开始时间会获得不同的结果,因此RHC方法结果无法反映空域系统的实时状态,进而准确判定实时的空中交通密度情况。而动态协同方法基于航空器实时位置信息触发排序,所得结果与排序开始时间无关。 图7 RHC方法在不同排序开始时间情况下的结果对比Fig.7 Results comparison of RHC method with different starting time of sequencing 图8为RHC方法和动态协同方法每次排序时涉及的航班个数及其在排序时段内出现的次数统计。由图8可见,对于时段1(时段2),RHC方法共进行了36次(36次)排序,动态协同方法共进行了28次(25次)排序,减少了8次/22.2%(11次/30.6%)。因为在对进场航班排序时不希望出现无航班需进行排序和仅有1个航班需进行排序的情况,故出现此2种情况的次数越少,排序的效率越高。对于时段1(时段2),RHC方法存在4次(4次)无航班需进行排序和10次(9次)仅有1个航班需进行排序的情况,而动态协同方法不存在无航班需进行排序和存在4次(3次)仅有1个航班需进行排序的情况,排序效率有所提高。 图8 RHC方法和动态协同方法结果对比Fig.8 Comparison of results between RHC method and dynamic collaborative method 4.2.2 先到先服务方法与动态协同方法对比 在时段1(时段2)内,动态协同方法共包括28个(25个)排序阶段:高密度2个(2个),中密度6个(10个),低密度20个(13个)。仿真结果表明,各密度条件下算法运行时间均小于1 s,且随着遗传算法进化代数的增加,各密度条件下种群中的个体均朝着最优化方向进化,故其能快速获得最优解。较先到先服务方法,对时段1(时段2)而言,高密度条件下各排序阶段最后一个进场航班的落地时间平均提前203.5 s(196 s);中密度条件下各排序阶段航班延误总时间平均减少30.8%(27.4%),航班延误均衡性平均提高35.5%(31.9%);低密度条件下在航班正常率及航班延误公平性得到保证的前提下,满足时隙交换规则的排序阶段均增加了1种进场航班排序模式。 以下对各交通密度条件下,使用先到先服务方法和基于空中交通密度的进场航班协同排序模型(以下简称优化模型)的排序结果作详细的对比讨论。 1) 高密度 图9为时段1第11个排序阶段最后1个进场航班的落地时间(优化目标1)在不同进化代数对应的种群个体平均目标函数值和最优个体目标函数值的变化趋势。从图中可以看出,随着种群的不断进化,种群个体的平均和最优目标函数值变化趋势一致,均朝着优化的方向变化。从种群最优个体目标函数值曲线中可以看出,在50代以内,最优目标函数值迅速由44 292 s下降到44 173 s 后不再发生变化。从种群个体平均目标函数值曲线中可以看出,种群的平均目标函数值迅速由44 624 s下降到44 200 s后趋于稳定,种群收敛。 图9 种群进化过程中目标函数值变化趋势(时段1-11)Fig.9 Trend of objective function value in population evolution process (time interval 1-11) 图10为时段1第11个排序阶段优化模型排序结果与先到先服务排序结果的对比。由图可见,相对于先到先服务排序结果,优化模型排序结果中的CSH9115落地次序推迟,GCR7804落地次序提前,且次序变化量都为1,此结果验证了本文将MPS约束转化为管制负荷限制时间窗的可行性。先到先服务排序结果最后一个进场航班的落地时间为44 413 s,优化模型排序结果为44 173 s,落地时间提前了240 s,即对于此排序阶段可多容纳2架进场航班落地。 图10 不同策略下进场航班计划落地时间(时段1-11)Fig.10 Scheduled landing time of arrival flights using different strategies (time interval 1-11) 图11为时段2第6个排序阶段最后一个进场航班的落地时间(优化目标1)在不同进化代数对应的种群个体平均目标函数值和最优个体目标函数值的变化趋势。从图中可以看出,随着种群的不断进化,种群个体的平均和最优目标函数值变化趋势一致,均朝着优化的方向变化。从种群最优个体目标函数值曲线中可以看出,在150代以内,最优目标函数值迅速由66 618 s下降到66 471 s;在150代~263代,最优目标函数值由66 471 s平缓的下降到66 461 s;263代以后,最优目标函数值不再发生变化。从种群个体平均目标函数值曲线中可以看出,种群的平均目标函数值迅速由66 664 s下降到66 500 s后趋于稳定,种群收敛。 图11 种群进化过程中目标函数值变化趋势(时段2-6)Fig.11 Trend of objective function value in population evolution process (time interval 2-6) 图12为时段2第6个排序阶段优化模型排序结果与先到先服务排序结果的对比。由图可见,相对于先到先服务排序结果,优化模型排序结果中的CSN6654落地次序推迟,CSZ9123落地次序提前,且次序变化量都为1,此结果同样验证了本文将MPS约束转化为管制负荷限制时间窗的可行性。先到先服务排序结果最后一个进场航班的落地时间为66 613 s,优化模型排序结果为66 461 s,落地时间提前了152 s,即对于此排序阶段可多容纳1架进场航班落地。 图12 不同策略下进场航班计划落地时间(时段2-6)Fig.12 Scheduled landing time of arrival flights using different strategies (time interval 2-6) 可见,在高密度条件下,使用优化模型排序方法可使得最后一个进场航班的落地时间提前,进而实现提升跑道容量的目标。 2) 中密度 图13为时段1第6个排序阶段内的航班延误均衡性(优化目标2)在不同进化代数对应的种群个体平均目标函数值和最优个体目标函数值的变化趋势。从图中可以看出,随着种群的不断进化,种群个体的平均和最优目标函数值变化趋势一致,均朝着优化的方向变化。从种群最优个体目标函数值曲线中可以看出,在90代以内,最优目标函数值迅速由1 743 s下降到672 s;在90代至121代,最优目标函数值由672 s平缓的下降到656 s;121代以后,最优目标函数值不再发生变化。从种群个体平均目标函数值曲线中可以看出,种群的平均目标函数值迅速由3 078 s下降到1 280 s后趋于稳定,种群收敛。 图13 种群进化过程中目标函数值变化趋势(时段1-6)Fig.13 Trend of objective function value in population evolution process (time interval 1-6) 图14为时段1第6个排序阶段优化模型排序结果与先到先服务排序结果的对比。由图可见,先到先服务排序结果和优化模型排序结果各航班落地次序相同。先到先服务排序结果的所有进场航班延误总时间为765 s,优化模型排序结果的所有进场航班延误总时间为481 s,减少了284 s (37.1%);先到先服务排序结果的航班延误均衡性为1 100 s,优化横型排序结果的航班延误均衡性为656 s,提高了444 s(40.4%)。对具体的航班而言,先到先服务排序结果中后3架航班均发生延误,分别为CDG4801延误142 s、CCA8128延误335 s、CXA8033延误288 s。由于CDG4801的尾流等级为中级,而在其前落地的KAL805的尾流为重级,因此二者之间需要满足较大的间隔要求,后续落地的CCA8128和CXA8033均存在较大延误的原因是CDG4801延误的传递。优化排序结果中KAL805和CDG4801分别提前 175 s 和33 s,CCA8128和CXA8033分别推迟160 s和113 s,优化排序结果中前机提前落地,减弱了前机延误对后机的影响,在一定程度上避免了延误的传递,可见优化排序结果将延误均衡化。 图14 不同策略下进场航班计划落地时间(时段1-6)Fig.14 Scheduled landing time of arrival flights using different strategies (time interval 1-6) 图15为时段2第18个排序阶段内的航班延误均衡性(优化目标2)在不同进化代数对应的种群个体平均目标函数值和最优个体目标函数值的变化趋势。从图中可以看出,随着种群的不断进化,种群个体的平均和最优目标函数值变化趋势一致,均朝着优化的方向变化。从种群最优个体目标函数值曲线中可以看出,在50代以内,最优目标函数值迅速由714 s下降到206 s;在39代至159代,最优目标函数值由206 s平缓的下降到200 s;159代以后,最优目标函数值不再发生变化。从种群个体平均目标函数值曲线中可以看出,种群的平均目标函数值迅速由3 044 s下降到638 s后趋于稳定,种群收敛。 图15 种群进化过程中目标函数值变化趋势(时段2-18)Fig.15 Trend of objective function value in population evolution process (time interval 2-18) 图16为时段2第18个排序阶段优化模型排序结果与先到先服务排序结果的对比。由图可见,先到先服务排序结果和优化模型排序结果各航班落地次序相同。先到先服务排序结果和优化模型排序结果所有进场航班延误总时间均为133 s,但较先到先服务排序结果航班延误均衡性266 s,优化模型模型排序结果航班延误均衡性为200 s,提高了66 s(24.8%)。对具体的航班而言,先到先服务排序结果中仅CSC8128延误133 s;优化模型排序结果中OKA3084提前67 s,CSC8128推迟66 s,可见优化模型排序结果将延误均衡化。 图16 不同策略下进场航班计划落地时间(时段2-18)Fig.16 Scheduled landing time of arrival flights using different strategies (time interval 2-18) 在实际管制运行中,当2架进场航班间隔过小时,管制员通常使用“前快后慢”的方法拉开间隔,因此优化模型排序结果符合实际运行情况。在中密度条件下,优化模型排序结果均衡了总体延误和个体延误,并贴近实际运行,使用优化模型排序方法可有效提高延误均衡性。 3) 低密度 由于目标函数和约束条件可相互转换,本文在求解模型时将目标函数(3)转换为航班正常率为1的约束。 图17为时段1第5个排序阶段内的进场航班延误时间均值(优化目标4)和标准差(优化目标5)在种群进化完成时所得的Pareto最优解。 图17 Pareto最优解(时段1-5)Fig.17 Pareto optimal solution (time interval 1-5) 图18为时段1第5个排序阶段优化模型排序结果与先到先服务排序结果的对比。可知,优化模型排序结果提供了2种排序模式:① 与先到先服务排序结果相同;② 较先到先服务排序结果,CCA1678和CCA8225的落地次序互换。此优化结果保证了时隙交换的可行性,对国航而言,由于CCA1678和CCA8225的尾流等级均为中级,其可根据实际需要选择是否交换二者的落地次序。 图18 不同策略下进场航班计划落地时间(时段1-5)Fig.18 Scheduled landing time of arrival flights using different strategies (time interval 1-5) 图19为时段2第8个排序阶段内的进场航班延误时间均值(优化目标4)和标准差(优化目标5)在种群进化完成时所得的Pareto最优解。由图可见,此排序阶段仅存在1个Pareto最优解,即算法寻找到对于优化目标4和优化目标5均为最优的解。该最优解表明,此排序阶段的所有航班均无延误发生。 图19 Pareto最优解(时段2-8)Fig.19 Pareto optimal solution (time interval 2-8) 此阶段的进场航班为GCR7826和GCR7896,二者尾流等级为中级和重级,但由于此阶段的航班均属于同一航空公司,故满足时隙交换规则的要求。对天航而言,其可根据实际需要选择是否交换GCR7826和GCR7896的落地次序,若选择交换落地次序,则GCR7896最多可提前10分钟落地。因此,使用时隙交换方法的优化模型排序结果提供了2种排序模式:①与先到先服务排序结果相同;②较先到先服务排序结果,GCR7826和GCR7896的落地次序互换。图20为时段2第8个排序阶段优化模型排序结果与先到先服务排序结果的对比。 可见,低密度条件下,在航班正常率及航班延误公平性得到保证的前提下,进场航班排序的灵活性提高,实现了三方协同排序。 在理论层面上,本文基于以往的研究,所做的改进与主要区别如下: 1) 文献[9-10]对某一时段内的所有航班进行排序,执行一次算法的时间均超过10 min,排序的实时性稍差。本文基于进场航班ADS-B数据和飞行计划数据,设计了一种进场航班动态排序方法,将某一时段划分为多个排序阶段,并且在各排序阶段内算法运行时间均小于1 s,实现了进场航班实时、动态和自动化排序。 2) 文献[9]提出了“多元受限时间窗”的概念,本文在此基础上进行改进:① 在可接受延误时间窗中,考虑机场和航空公司双方的诉求,将机场基地航空公司航班的重要度设置为次高等级;② 提出了“管制负荷限制时间窗”的概念,建立了MPS约束和航班计划落地时间之间的关系。 3) 文献[9-10]均使用了航班延误总时间最小作为目标函数之一,本文提出“航班延误均衡性”的概念,综合考虑航班总体延误时间和个体延误时间,将航班总体和个体延误均控制在较低水平。 在实践应用层面上,本文基于以往的研究,所做的改进如下: 1) 本文深入分析管制运行特性,充分考虑管制负荷对进场航班排序的影响,对空中交通密度进行分类,在各密度条件下选择合理的优化目标与排序方案,建立了基于空中交通密度的进场航班协同排序模型。 2) 在管制运行中优先保障重要度高的航班,其通常提前到达,但不可推迟到达;重要度低的航班可提前亦可推迟到达。基于此,本文将文献[9]的“最大可接受延误时间”细化,提出“可接受的最大提前到达时间”和“可接受的最大推迟到达时间”。 3) 在实际运行中,航空公司从商业角度出发,基于对本公司的商业利益等多方面综合考虑,对于航班的重要性分析与管制单位的分析存在差异。因此在CDM的理念下,本文设计了一种时隙交换方法以充分考虑航空公司对于进场航班排序的决策因素。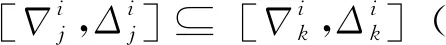
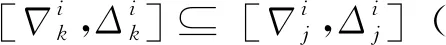

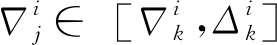
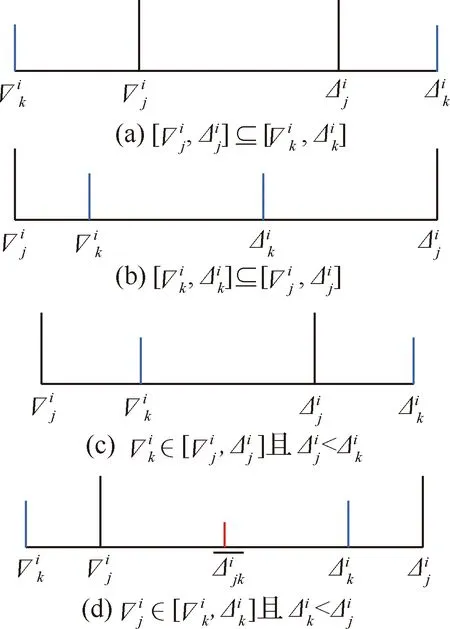

2.3 时隙交换方法
2.4 基于空中交通密度的进场航班协同排序模型
3 算法设计
3.1 算法流程

3.2 算法实现
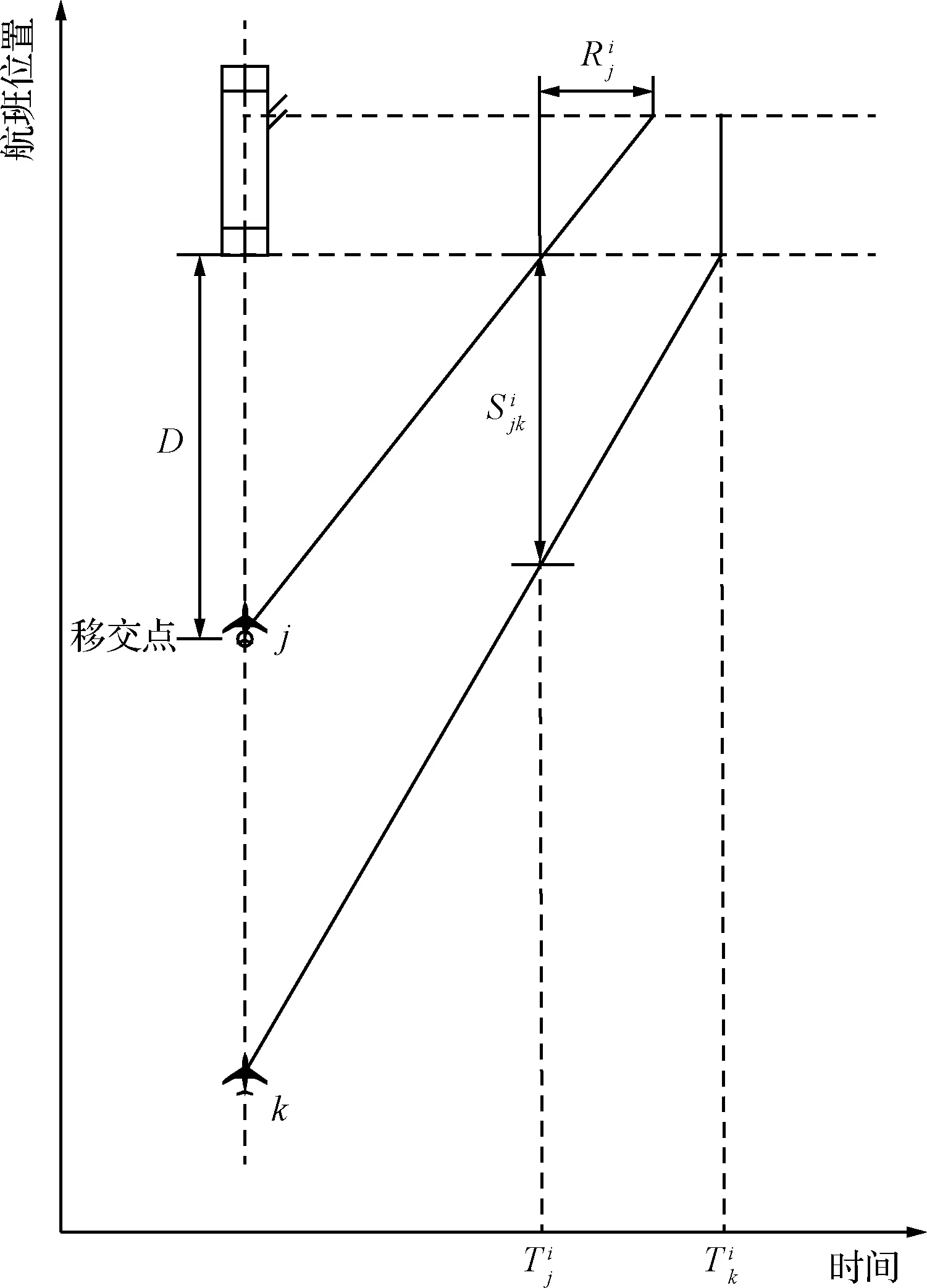
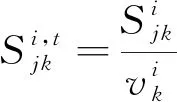



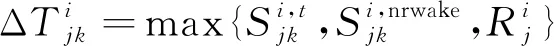

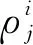
4 实例验证
4.1 实验设计

4.2 结果分析









5 结 论
