基于改进A-Star算法的隐身无人机快速突防航路规划
2020-07-30张哲吴剑代冀阳应进何诚
张哲,吴剑,2,*,代冀阳,应进,何诚
1. 南昌航空大学 信息工程学院,南昌 330063 2. 北京航空航天大学 可靠性与系统工程学院,北京 100083
在现代战争中,随着隐身与反隐身技术的快速发展,现代战区立体防空体系部署日益严密,飞行器仅仅依靠传统突防模式下的航迹规划技术实现战区突防已经越来越难[1]。如何在严密的组网雷达系统威胁下,为隐身无人机快速地规划出具有高安全性的突防路线是当前面临的一个重大难题[2-4]。
雷达的探测能力与目标的雷达散射截面(Radar Cross Section,RCS)有关。由于隐身无人机全向的部分角域具有较小的RCS值,通过调整隐身无人机的姿态角,使得这些具有较低RCS值的角域面向雷达时,能够大幅度地降低雷达检测概率,从而保证隐身无人机的安全突防[5]。此外,现有雷达系统只有在多次扫描获取的目标信号满足一定准则时,才会做出有效的判决。因此,在复杂的战场环境下,结合飞行器全向的动态RCS特点和雷达发现准则这2个因素,选用合适的突防飞行路线,便能够保证隐身无人机能够在复杂的战场环境中实现安全、快速突防。
目前大部分航路规划研究主要集中在离线规划、在线规划或是航迹优化等方面[6-8],通常将雷达威胁以固定的威胁区域放置于二维或三维空间进行讨论,较少考虑飞行器全向RCS值及雷达发现准则等因素,这些研究显然无法满足隐身无人机在复杂环境中的突防需求[9]。文献[10-13]通过建立动态RCS模型来获取目标更准确的全向RCS值,从而更好地反映目标时刻所处的威胁状态。文献[14-15]分析雷达工作机理,以一定扫描周期内的发现概率均值来体现目标被确认发现的概率。这两部分的研究为飞行器实现快速、安全的战区突防奠定了重要的理论基础。
本文结合隐身无人机突防过程中的动态RCS特性和雷达发现准则,建立了隐身无人机运动学模型和组网雷达探测概率模型。充分考虑了所规划航路的快速性和安全性,采用A-Star算法进行突防航迹规划,对隐身航路的实际需求进行了算法改进:① 在A-Star算法搜索过程中引入了含有加权因子的多层变步长搜索策略;② 在算法搜索节点中添加隐身无人机的姿态角信息;③ 在 航迹节点中考虑雷达的秩K融合准则[16],以此来判断新航迹点的可行性。分别在单雷达和组网雷达系统环境下,运用改进A-Star算法与传统A-Star算法进行仿真实验对比,结果表明在复杂的组网雷达威胁环境下,改进算法用于隐身无人机,能够实现其快速、安全的战区突防,从而进一步验证了所提出的改进A-Star算法的有效性。
1 隐身无人机突防过程建模与分析
在现代空战的防御体系中,组网雷达系统根据空中目标的RCS,能够从多个站点对指定的空域进行全面探测,对整个空域范围内的目标实现全方位的定位、识别和跟踪。因此,组网雷达的广泛应用,极大程度地提高了飞行器在空域内的突防难度。
隐身无人机在设计时,通常根据雷达的几种波段,对机头、机身和尾翼等雷达重点照射角域进行RCS减缩,这样能够大大减小雷达的探测概率,降低系统的战斗效能,从而提高隐身无人机的突防能力和生存能力。
1.1 隐身无人机运动学模型
隐身无人机在飞行中为了节省燃油消耗,更好地展现隐身性能实现战区突防,通常会在固定高度保持巡航状态,尽量不做出大规模机动动作。结合隐身无人机的运动学特性,对其进行建模分析。
本文将隐身无人机认为是一个带有姿态信息的质点,以恒定的速度v在固定高度h下做小机动动作或转弯飞行。因此建立隐身无人机的运动学模型,即
(1)
式中:x、y分别为无人机在地理坐标系中的位置;φ为无人机的航向角;θ为无人机的滚转角;v为无人机的飞行速度;g为重力加速度。
考虑无人机在空域水平飞行中的小机动动作和转弯运动,由于保持定高飞行模型,因此隐身无人机的运动状态如图1所示。
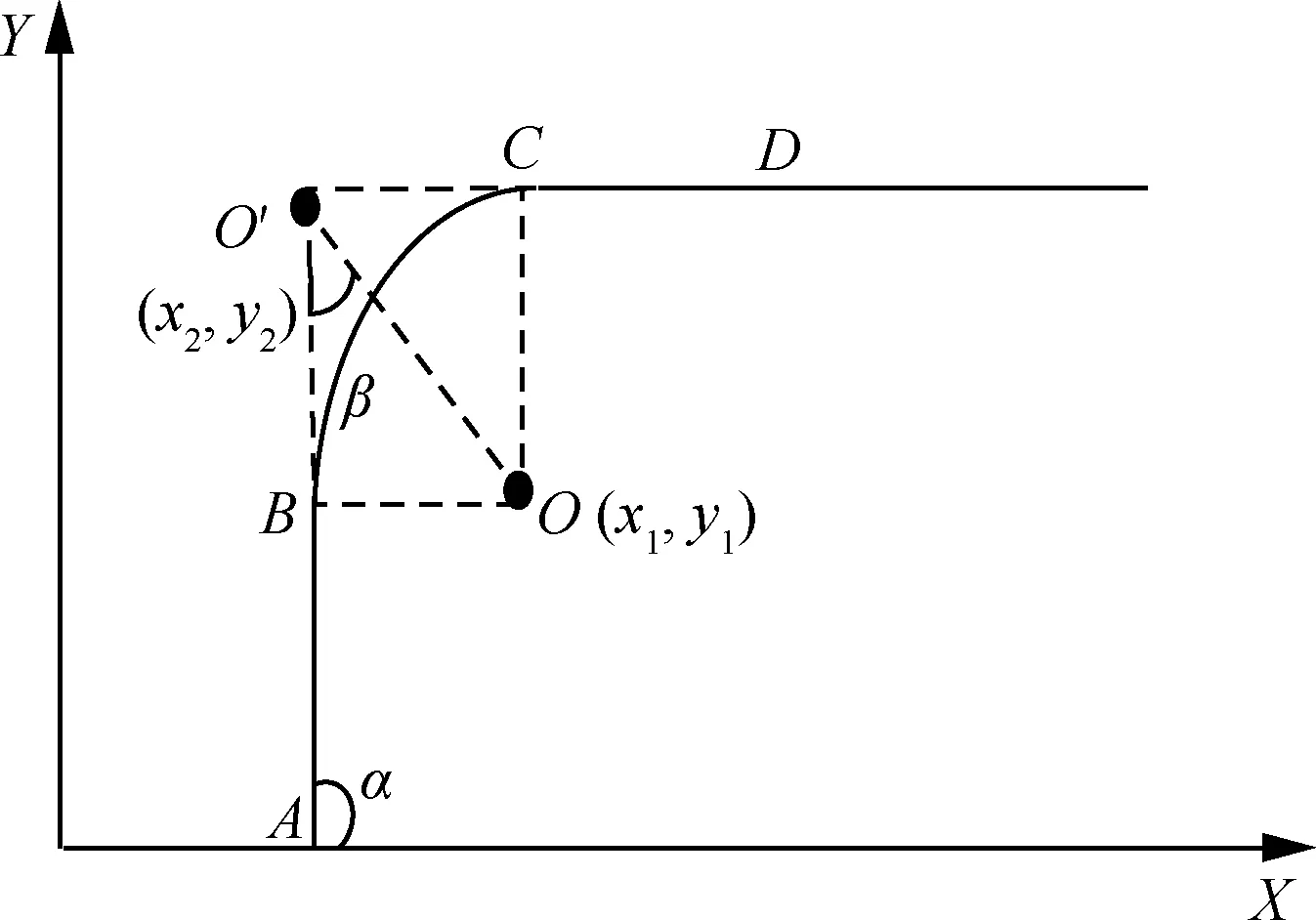
图1 隐身无人机的运动状态Fig.1 Movement state of stealth UAV
假设已给出直线段的路线参数和转弯半径,由图1可知,线段AB和线段CD分别为无人机转弯前的飞行路线。圆弧BC为无人机转弯过程中的轨迹。因此,圆弧的中心坐标可以表示为
(2)
式中:(x1,y1)为点O的坐标;O′为AB和CD两条线段延长线的交点;b为AO′与BO′长度的比例系数;α为航线与水平方向的夹角;β为航迹延长线与转弯半径延长线的夹角。
无人机在转弯过程中由于滚转角θ的变化,会增大被雷达所探测到的概率,从而大大提高了隐身突防难度。因此,为了保障无人机转弯过程中的安全,本文给出了无人机的2种转弯飞行模式[17],并进行了以下分析:
1) 最大负载飞行模式。无人机在转弯时保持较大的滚转角,这样可以保证转弯半径r最小,转弯所需时间最少,暴露于雷达中的时间相对较短。
2) 最小滚转角飞行模式。假设图1中线段AO′和BO′是无人机飞行中相邻的2个航线,当B点为线段AO′的中点,C点为线段O′D的中点时,无人机能够以最大转弯半径保持转弯飞行,这样便可以在飞行过程中始终保持相对较小的滚转角θ,大大降低了雷达系统的探测概率。
分析图1中航线的几何关系及式(2),可得无人机飞行中的转弯半径与航线段的关系式为
(3)
以rmin和rmax分别表示无人机的最小转弯半径及最大转弯半径,由式(3)计算可得无人机飞行过程中的最大转弯半径为
(4)
用θmax和θmin分别表示无人机飞行时的最大滚转角和最小滚转角,分析式(1)中无人机的运动学模型及图1中的航线几何关系,可以计算得到:
(5)
通过对隐身无人机运动学模型的求解,充分考虑无人机的姿态角信息,从而更好地分析隐身无人机突防的航路变化及精准计算雷达的探测概率。
1.2 动态RCS特性
隐身无人机的RCS是影响雷达探测概率的关键因素之一,对无人机实现战区的隐身突防有直接的影响。一般的航迹规划问题通常将RCS视为固定值,但在实际中并不合理。目标无人机的RCS值会根据雷达波照射方向的不同而变化,不同视线方向上的RCS具有剧烈起伏的特点。而且,某一方向上的无人机RCS的大小还与入射雷达波的频率、雷达天线的极化方向这2个因素有关[1]。因此,无人机在进行隐身设计时,通常会在防空雷达的几种常用波段(如S、C波段)以及水平(Horizontal and Horizontal,HH)极化和垂直(Vertical and Vertical,VV)极化方式下,对无人机的重点角域进行RCS减缩。
隐身无人机在飞行过程中,其与各部雷达相对姿态角的改变,使得雷达探测到的无人机的RCS值也会不断变化,即呈现出动态RCS特性。为了充分利用隐身无人机的动态RCS特性进行快速突防,需要采用更完整的RCS周向数据来进行航迹规划。本文根据数值计算和微波的实验数据,以RCS数据表[18]作为动态RCS特性来分析。若无人机不进行频繁大机动飞行时,可仅取水平照射一定俯仰角范围内的数据。
1.3 雷达的探测概率
雷达系统会对指定空域进行反复扫描,在有效作用范围内,用雷达检测概率表示雷达在某段时间内能够连续获得目标信息的可能性,每次进行的空域扫描都会以一定的检测概率来获取目标信号。当所获得的目标信息满足常用的航迹准则时,雷达系统确认发现目标,并将所获取的目标信息传递至系统的信息融合中心。下面分别讨论在单雷达和组网雷达下系统对目标的探测概率。
1.3.1 单雷达系统的探测概率
对于给定的单雷达系统,当其检测概率和虚警概率确定时,对无人机目标的探测概率只与无人机到雷达中心的距离和RCS值有关。在一段时间内,通过累计雷达对无人机目标的多次瞬时探测概率,可以计算得到雷达探测概率为
(6)
式中:P为雷达探测概率;Pt为瞬时探测概率;T为雷达扫描周期;t为当前时刻;Ri为无人机到第i个雷达中心的距离;σ为无人机的RCS值;c1和c2为由雷达自身性能确定的参数[1,18]。
然而在实际的突防飞行过程中,隐身无人机按照某一航路飞过雷达区域时会经历多次雷达探测,由于每次探测时无人机的RCS值、与雷达中心的距离和姿态角均不同,造成雷达在无人机各航迹点的探测概率也不同。为了更客观地反映隐身无人机在雷达系统探测下整个航路受到威胁的情况,将雷达系统的各次瞬时探测概率进行累加,即对式(6)中无人机探测概率作离散化处理,得到单雷达系统下的无人机探测概率为

(7)
式中:s为雷达扫描次数;pi为雷达对无人机的第i次探测的瞬时探测概率。
1.3.2 组网雷达系统的探测概率
对于完整的组网雷达系统,内部各雷达的联网可以显著提高系统对无人机的探测概率。组网雷达系统的探测概率主要是指信息融合中心计算得出的目标发现概率。在现代的组网雷达系统中,秩K融合规则应用广泛。因此,采用秩K融合规则对组网雷达探测概率进行深入分析。
设组网雷达系统中有M部雷达,由秩K融合规则,当系统内发现目标无人机的雷达数量超过最优检测门限K0时,即认为雷达发现该目标,当组网雷达对无人机的融合探测概率Pd∈[0.5,0.9],组网雷达系统的融合虚警概率Pf∈[10-9,10-5]时,最优检测门限K0的近似值为
(8)
秩K融合规则判决流程如图2所示。每部雷达根据自身对隐身无人机的探测做出局部判断,判决结果非0即1,取决于局部门限检测目标是否存在。由二元假设为H0和H1,H0表示目标不出现,H1表示目标出现。因此第j个雷达的决策值dj(j=1,2,…,M)可以表示为

图2 秩K融合规则判决流程Fig.2 Rank K fusion rule decision process
(9)
然后将局部判决结果传递至雷达系统的信息融合中心,构成全局判决空间D,即D={d1,d2,…,dM},组网雷达信息融合规则记为R,则秩K融合的判决规则R(D)可以表示为

(10)
此时,组网雷达系统对无人机的总探测概率为
(11)
式中:集合S1是使融合中心判为1的局部判决向量所构成的集合,由融合规则R(D)确定;集合S0是使融合中心判为0的局部判决向量所构成的集合;Pdj为组网雷达系统内第j个雷达对无人机的探测概率。
同理可知,整个组网雷达系统的虚警概率PF为
(12)
2 突防航迹规划算法
A-Star算法作为一种启发式搜索算法,广泛应用于各类智能体的路径规划问题中[19-21]。本文引入A-Star算法用于隐身无人机的战区突防航路规划,从隐身无人机航路搜索的快速性和安全性两方面入手进行深入分析。
2.1 算法描述
在标准A-Star算法的航路搜索过程中,通过设定合适的启发函数,全面估计待搜索区域可扩展搜索点的代价值,通过比较各点不同代价值的大小,兼顾考虑航迹点搜索的运算时间与距离代价,找出一条最优的航路。在A-Star算法中,通常利用对OPEN表和CLOSE表的操作来实现航迹点的存储和更新。算法的寻优运算可以表示为
f(n)=g(n)+h(n)
(13)
然而采用标准A-Star算法搜索产生的航路存在以下不足:① 只能反映无人机的位置信息,无法体现隐身无人机的动态RCS特性及姿态信息;② 并且未考虑雷达探测概率,仅仅通过比较各相邻扩展点的代价大小来判断航迹点的可行性;③ 在航路搜索过程中未知路径代价估值的h(n)在路径还未被完全扩展之前无法精确计算,最终设计的路线可能不是全局最优解且运算时间较长。因此,对传统A-Star算法进行改进,对航迹点的扩展搜索方式、步长值、新航迹点的可行性判定及运算时间等进行优化改进。
2.2 改进A-Star算法
2.2.1 无人机姿态角信息融合
结合隐身无人机的动态RCS特性,在A-Star算法节点中添加了无人机的姿态角信息。首先将A0(x0,y0)作为第1个扩展节点放入OPEN表中,由相邻节点总代价值向待搜索区域进行扩展;然后,比较各节点的代价值大小,选取所有节点中总代价值f(n)最小的点,作为新的航迹节点An(xn,yn),同时生成新节点处的航向角φn。最后,在等高和匀速小机动飞行模式下,结合式(1),在An处父节点的滚转角θn可表示为
(14)
式中:φn为与航迹新节点相邻的各节点的航向角;φs为周围节点的航向角;η为扩展搜索的步长。
此外,在对待扩展区域的搜索过程中,相邻航迹节点之间的航向角变化需要满足最大转向角速度的约束,即
(15)
因此,可以得到扩展搜索过程中在An处无人机飞行时的姿态角信息(θn,φn),再结合式(6)~式(8),便可计算出各时刻An节点处的雷达探测概率Pt。
2.2.2 多层变步长策略
标准A-Star算法利用OPEN表进行寻优运算时,无法对待搜索区域内未知路径的代价值进行准确的计算,通常采用当前节点与下一步的目标扩展节点的直线距离来估计,显然无法保证这段航迹点的精度及整段航线的安全性[22-23]。因此,引入一个加权因子ω,其中ω>1,此时f(n)的表达式为
f(n)=g(n)+ωh(n)
(16)
这意味着增大了未知路径代价在总路径代价的占比,即增加了A-Star算法的搜索深度,防止算法陷入局部搜索的死区中,保证了最优解的质量。
为保证隐身无人机在复杂的组网雷达系统下实现快速突防,需要对传统A-Star算法的搜索方式进行改进,来提高整个突防过程中航迹点搜索效率。因此,设计了一种多层变步长的搜索方式来进行运算寻优。
在算法搜索过程中,由第k步已扩展点Ak(xk,yk)至第k+1步可扩展点Bk(xk+1,yk+1)坐标为
(17)
式中:φi和Lj分别为拓展搜索线段间的夹角与对应弧长,即
(18)
若该元素不与B阵中的其他元素重合,不在OPEN表或CLOSE表中,则该元素可扩展至CLOSE表。变步长搜索策略的拓展过程如图3所示。

图3 变步长搜索航迹点拓展过程Fig.3 Variable step size search track point expansion process
2.2.3 新航迹点的可行性判定
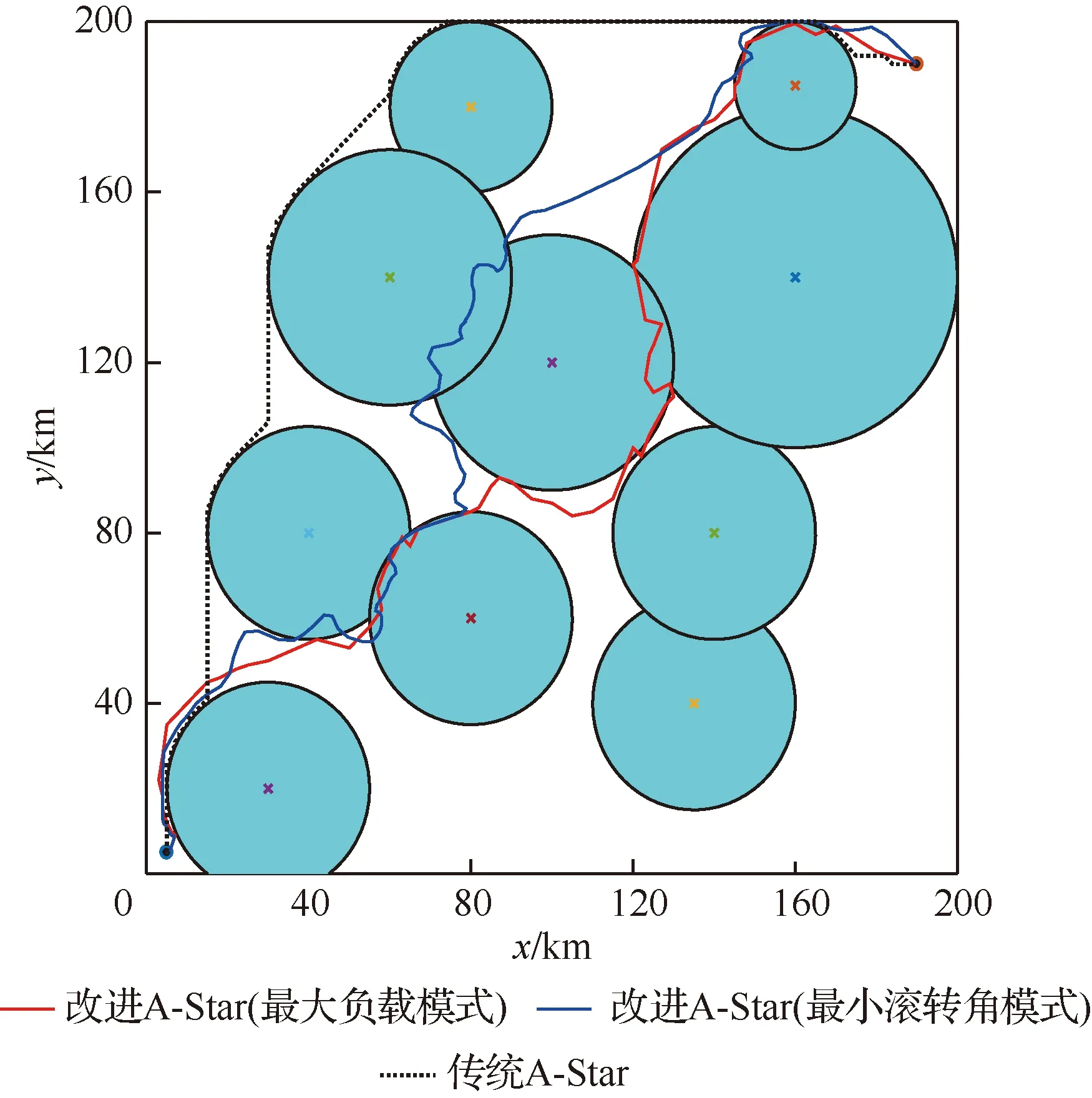
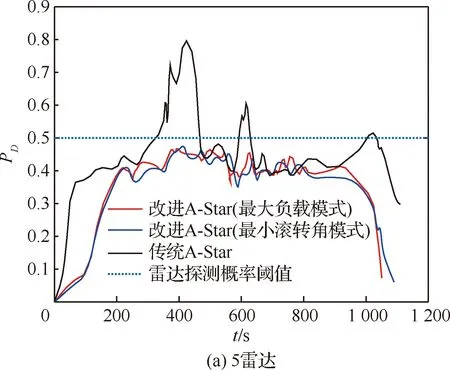
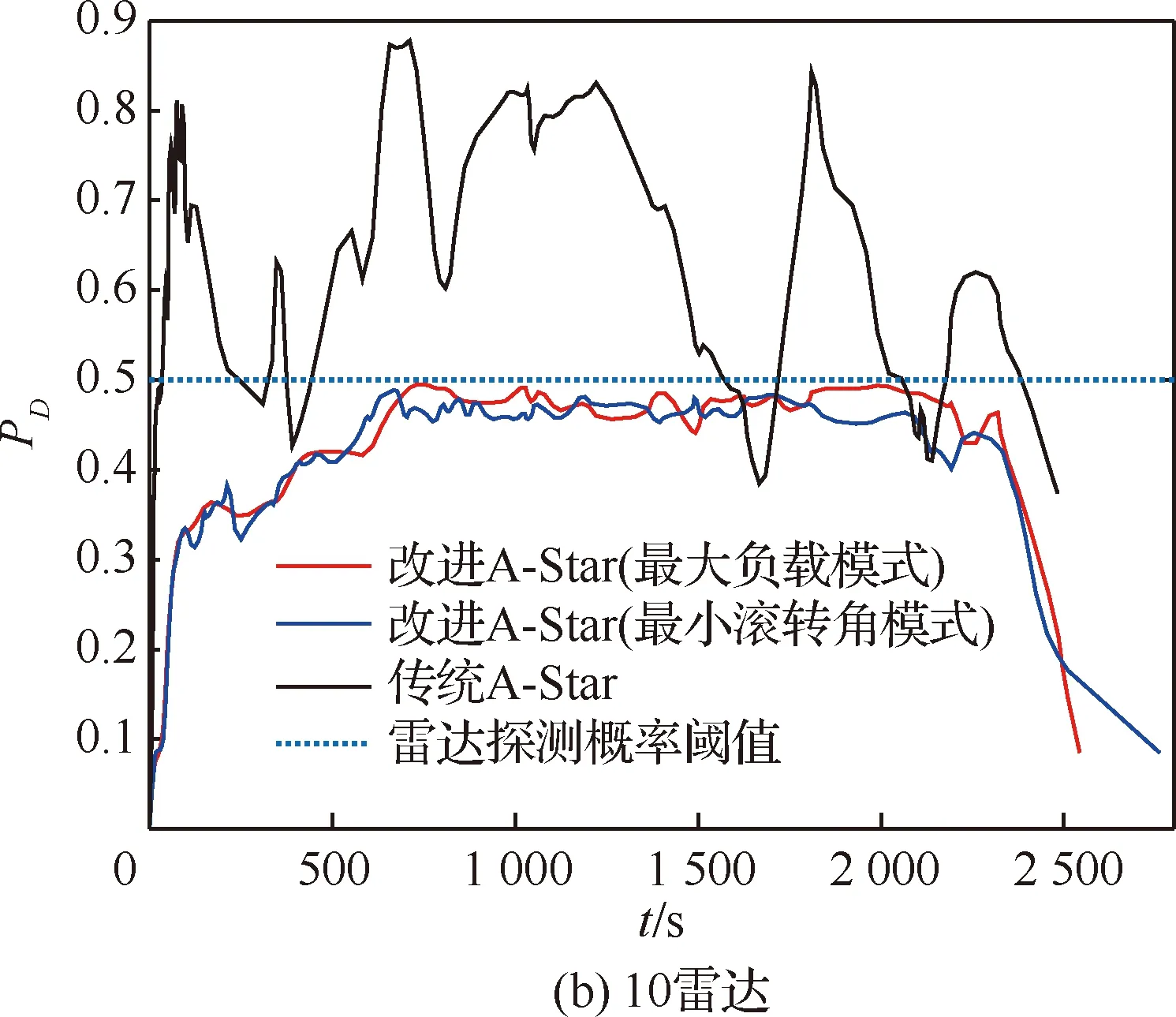
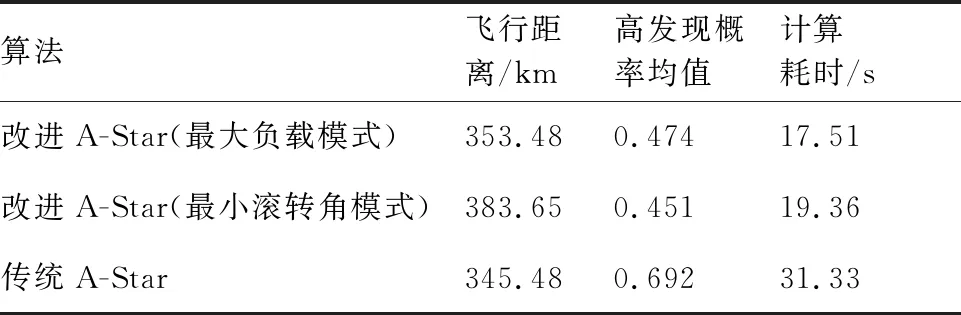
改进A-Star算法在对待扩展区域的搜索过程进行当前航迹节点An(xn,yn)扩展时,生成其相邻节点及其航向角和滚转角,由秩K融合规则的式(10)和式(11),计算对应节点该时刻的雷达探测概率;然后,结合当前节点与之前相邻节点的雷达探测概率,计算得到该航迹段上的探测概率Pn;最后,根据突防安全性要求,设定一个概率阈值Pc,若Pn 综上分析,可以给出改进A-Star算法的详细流程如图4所示。 图4 改进A-Star算法的流程图Fig.4 Flowchart of improved A-Star algorithm 为了验证模型及改进算法的有效性,在单雷达和组网雷达的战区防空系统下,分别采取最大负载飞行和最小滚转角飞行这2种转弯飞行模式,隐身无人机以速度v为500 km/h,高度为1 000 m,b=2,符合实际无人机运动状态,在匀速定高飞行下实现低空战区突防,并通过限制航向角φ使得无人机仅做小机动动作。所有雷达均采用秩K融合准则判定及计算无人机的探测概率,K0值由雷达数M确定,取s=3,改进A-Star算法搜索过程中的加权因子ω=1.5,初始的拓展搜索角度为6°,步长为2。设雷达对无人机的探测概率阈值Pc为0.5,当Pn>0.4时为雷达高发现的概率状态,用来评估该航迹段的安全程度,在仿真实验中,RCS表选取S波段HH极化数据,可得到某型隐身无人机的全向RCS数据,如图5所示。 图5 某型隐身无人机的全向RCS曲线(S波段HH极化)Fig.5 Omnidirectional RCS curve of a stealth UAV (S-band HH polarization) 设定100 km×100 km的无人机突防区域,单雷达系统中雷达的坐标为(50,50) km,无人机飞行起始点为(10,10) km,目标点为(80,80) km,分别采用改进A-Star算法和传统A-Star算法进行无人机隐身突防仿真,如图6所示。单雷达系统下的隐身无人机飞行数据见表1。 图6 单雷达系统下的突防仿真结果Fig.6 Penetration simulation results under single radar system 表1 单雷达系统下飞行仿真数据Table 1 Flight simulation data under single radar system 由图6中2种方法的仿真结果比较及表1的无人机飞行数据统计可知,在单雷达系统的战区突防环境下,改进A-Star算法通过控制隐身无人机在各航路点上的飞行姿态,实现了更有效和相对安全的航路突防。 由于组网雷达系统内的各种雷达覆盖范围互有重叠,因此相较于单雷达系统,其信息融合系统能够得到质量更好地目标航迹,极大提高了系统对目标的反低空突防能力。为了进一步验证改进A-Star算法的有效性,设定组网雷达系统中雷达数量分别为3、5和10这3种情景,各雷达性能参数略有不同,对隐身无人机进行战区突防仿真。 3.2.1 3雷达系统 在100 km×100 km的突防区域中,各雷达位置分别为:雷达1 (80,40) km,雷达2 (30,80) km,雷达3 (50,50) km。无人机飞行的起始点坐标(10,10) km,目标点坐标(90,90) km。分别采用改进A-Star算法和传统A-Star算法进行无人机隐身突防仿真,如图7所示。3雷达系统下的隐身无人机飞行数据见表2。 由图7中仿真结果及表2中的飞行数据统计可知,在3雷达系统的战区突防环境下,改进A-Star算法可以在雷达威胁密度较大的区域中实现隐身无人机安全突防。与传统A-Star算法相比,改进算法通过对各航迹点的变步长搜索,能够更加精确地调整隐身无人机的姿态,从而控制整段航路上各处的RCS值,得到更短的飞行距离和安全的航迹节点,实现快速、安全的战区突防航路规划。 图7 3雷达系统下的突防仿真结果Fig.7 Penetration simulation results under three radars system 表2 3雷达系统下飞行仿真数据Table 2 Flight simulation data under three radars system 3.2.2 5雷达系统 在100 km×100 km的突防区域中,各雷达位置分别为:雷达1 (50,50) km,雷达2 (30,20) km,雷达3 (75,80) km,雷达4 (40,80) km,雷达5 (80,60) km。无人机飞行的起始点坐标为(10,10) km,目标点坐标为(90,90) km。分别采用改进A-Star算法和传统A-Star算法进行无人机隐身突防仿真,如图8所示。5雷达系统下的隐身无人机飞行数据见表3。 表3 5雷达系统下飞行仿真数据Table 3 Flight simulation data under five radars system 图8 5雷达系统下的突防仿真结果Fig.8 Penetration simulation results under five radars system 3.2.3 10雷达系统 在200 km×200 km的突防区域中,各雷达位置分别为:雷达1 (135,40) km,雷达2 (30,20) km,雷达3 (140,80) km,雷达4 (40,80) km,雷达5 (80,60) km,雷达6 (160,140) km,雷达7 (160,185) km,雷达8 (80,180) km,雷达9 (100,120) km,雷达10 (60,140) km。无人机飞行的起始点坐标为(5,5) km,目标点坐标为(190,190) km。分别采用改进A-Star算法和传统A-Star算法进行无人机隐身突防仿真,如图9所示。10雷达系统下的隐身无人机飞行数据见表4。 图9 10雷达系统下的突防仿真结果Fig.9 Penetration simulation results under ten radars system 以雷达探测概率作为突防结果的影响因素,不同环境下的组网雷达探测概率如图10所示。 图10 典型威胁环境下不同算法的突防威胁概率Fig.10 Penetration threat probability of different algorithms in typical threat environment 由图8和图9中仿真结果及表3和表4可知,在5雷达系统和10雷达系统的典型威胁环境下,由于传统A-Star算法在航迹搜索过程中,计算得到部分航迹节点的雷达探测概率高于阈值,无法满足航路的安全性要求。因此,传统A-Star算法在实际的雷达威胁环境中应该是无航路规划结果的。但是,为了进一步分析,认为被探测概率即使超过阈值,无人机仍然可以向前突防,计算得到在5雷达和10雷达威胁环境下,无人机探测概率超过阈值的飞行时间分别为209.35 s和1 940.35 s。而改进A-Star算法仍然可以在雷达威胁密度较大的区域中实现隐身无人机成功突防,且整段航路的探测概率均小于阈值。与传统A-Star算法相比,改进算法充分利用各航迹点的变步长搜索策略和姿态变化,控制整段航路上各点的RCS值,能够满足隐身无人机战区突防中快速和安全这两点要求。 表4 10雷达系统下飞行仿真数据Table 4 Flight simulation data under ten radars system 1) 针对复杂的组网雷达系统下隐身无人机实现快速和安全的突防问题,提出了一种改进A-Star 算法的隐身无人机战区突防航路规划方法,并将其与传统A-Star算法进行比较,仿真结果表明改进算法优于传统算法。 2) 所设计的改进A-Star算法在对航迹节点的搜索过程中引入了多层变步长搜索策略和无人机的姿态角信息,加快了航路搜索的效率,体现了隐身无人机动态RCS的变化特性,为复杂战场环境中的隐身无人机突防提供了一定的军事应用价值。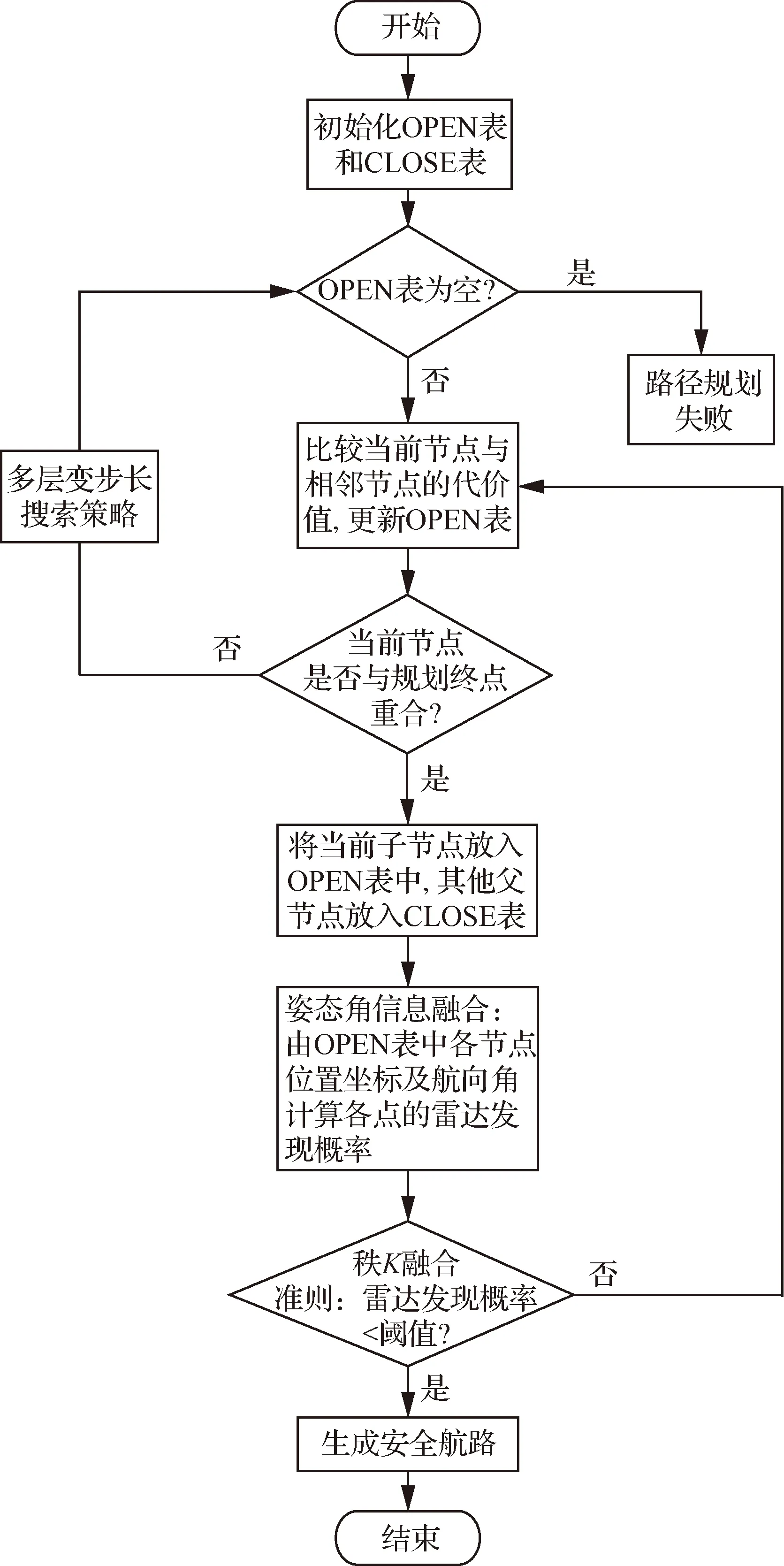
3 仿真实验分析
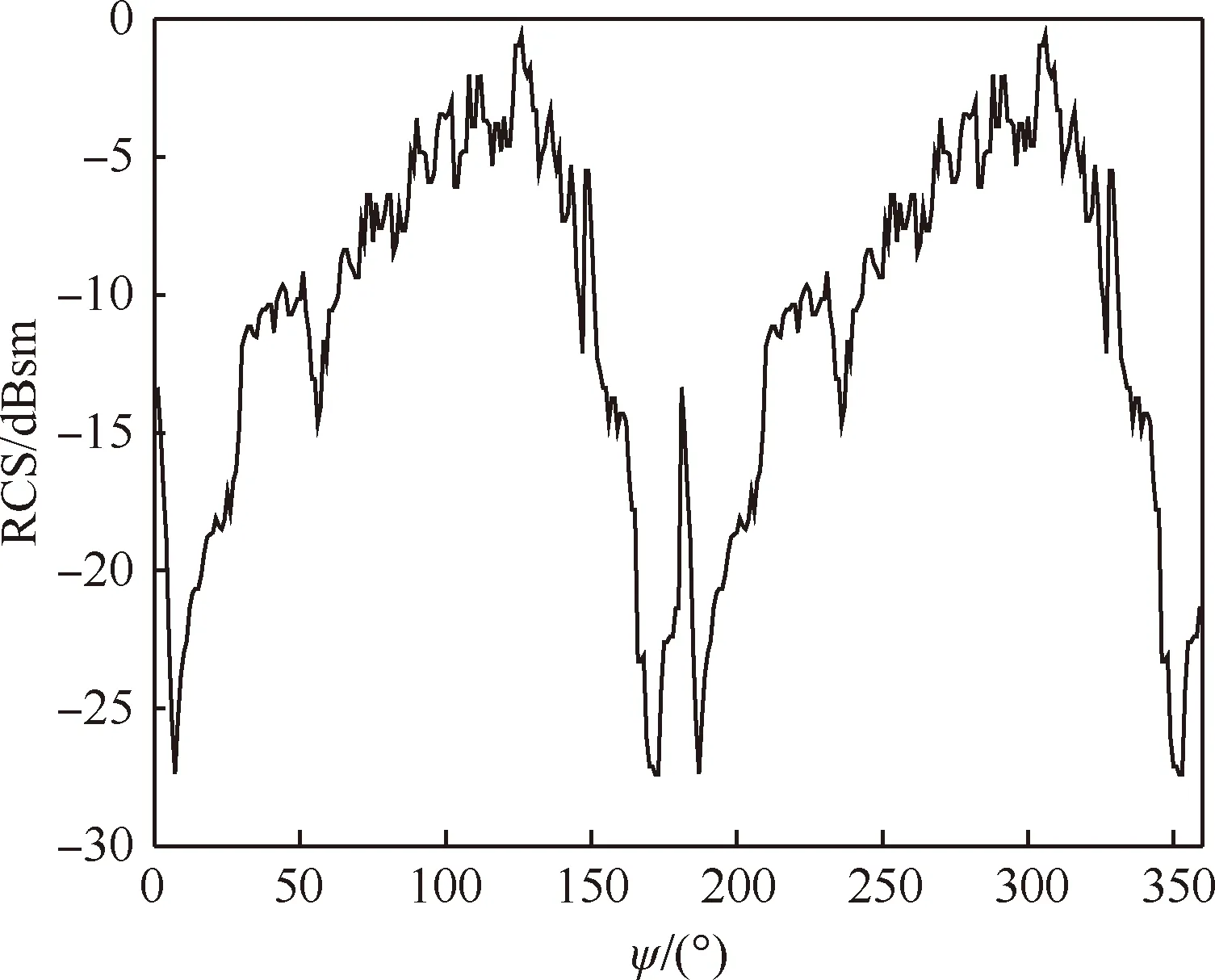
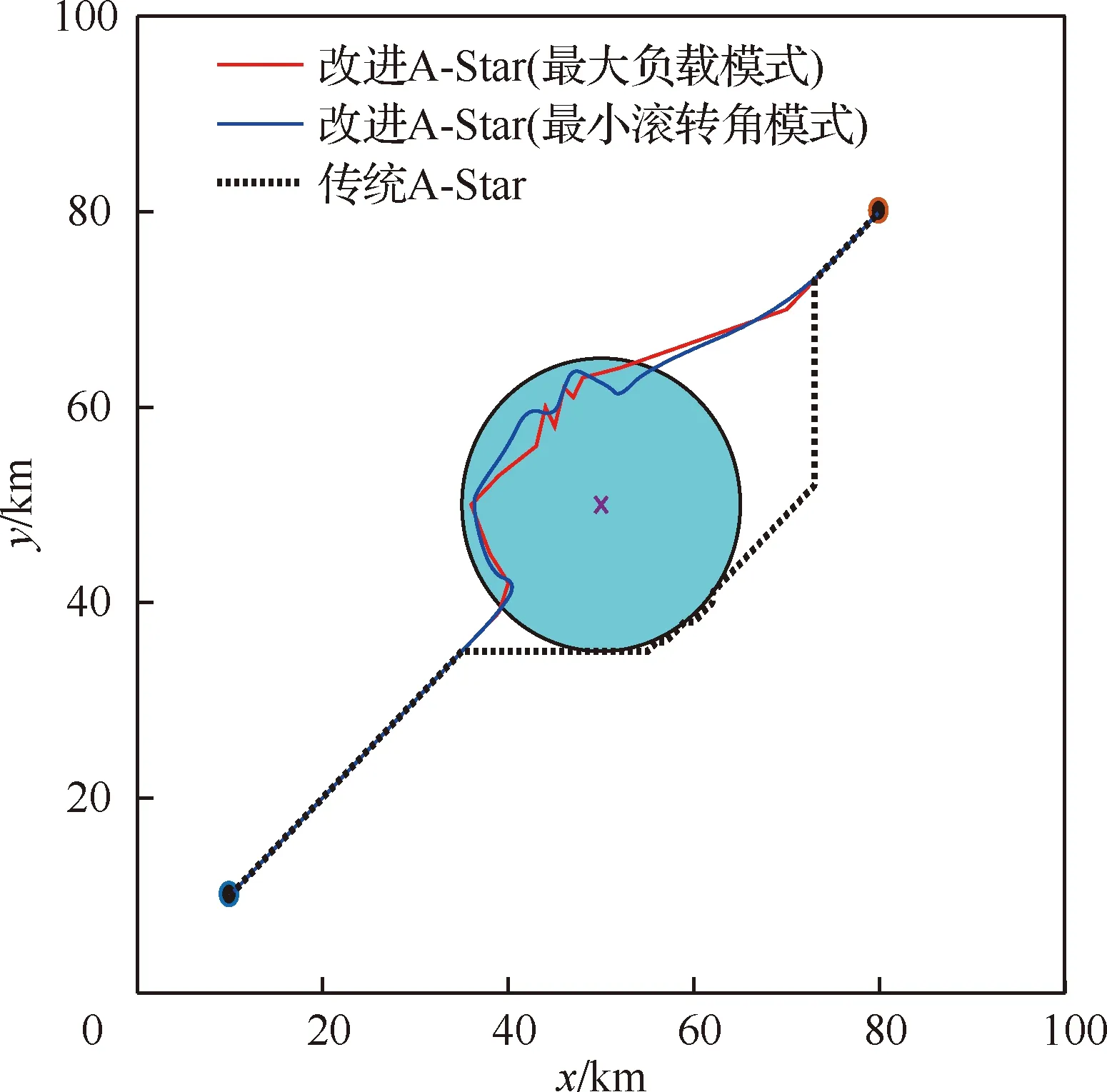
3.1 单雷达系统
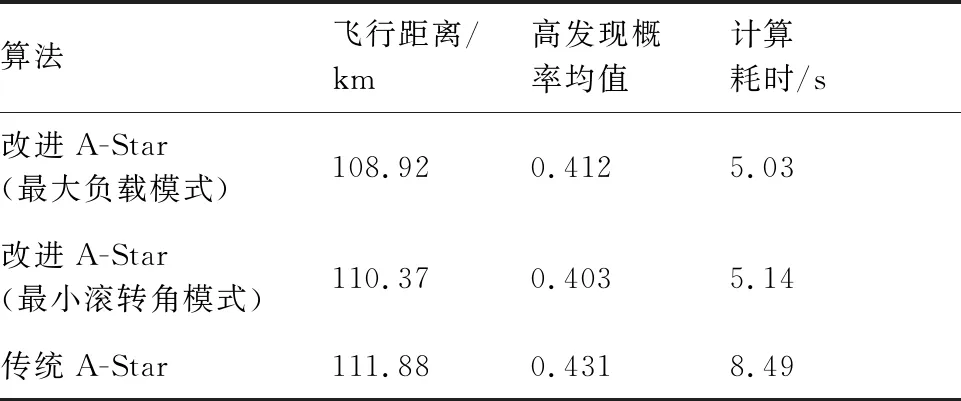
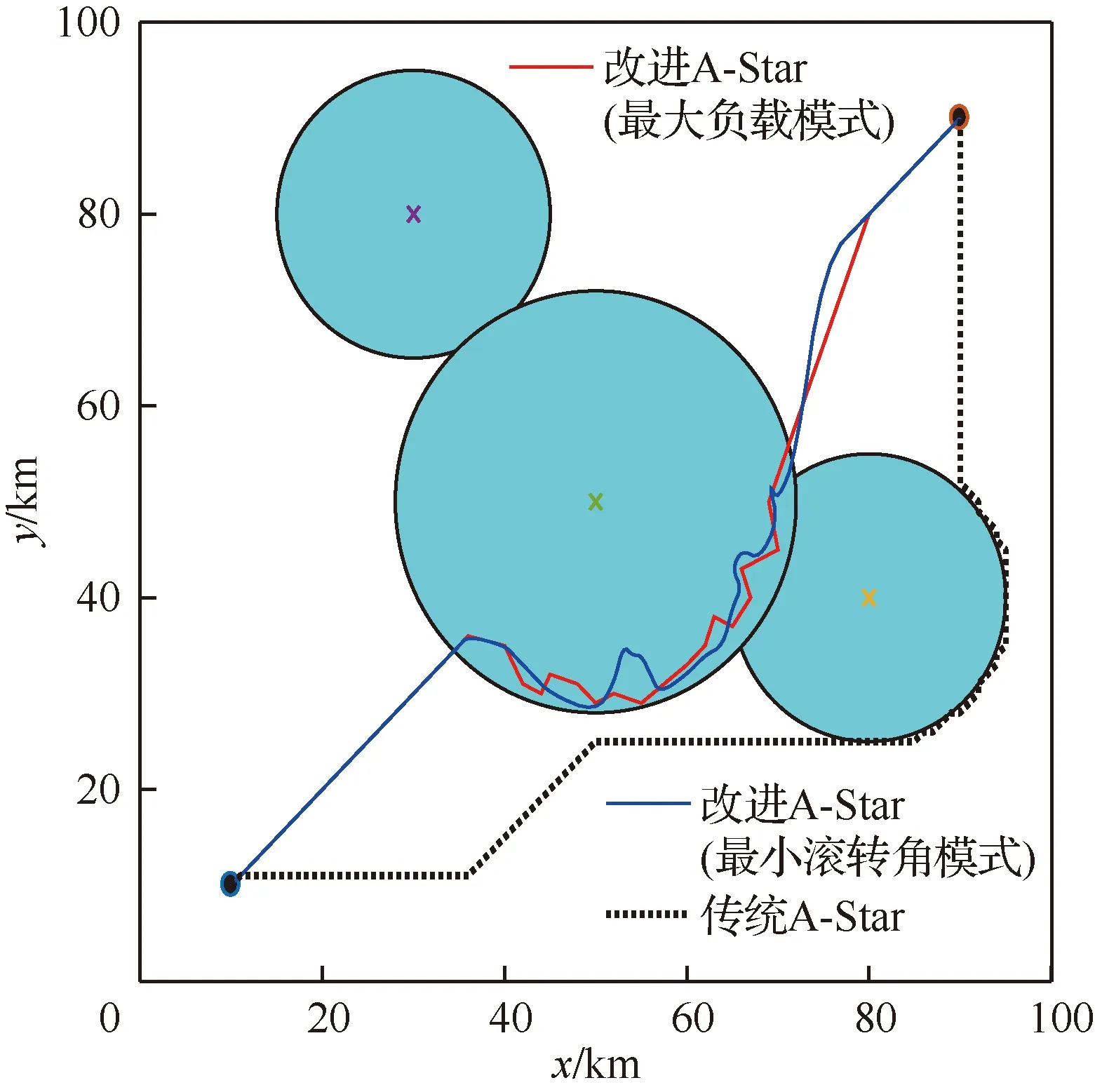
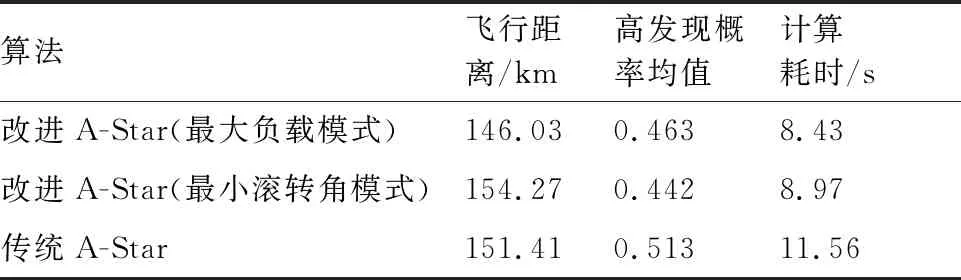
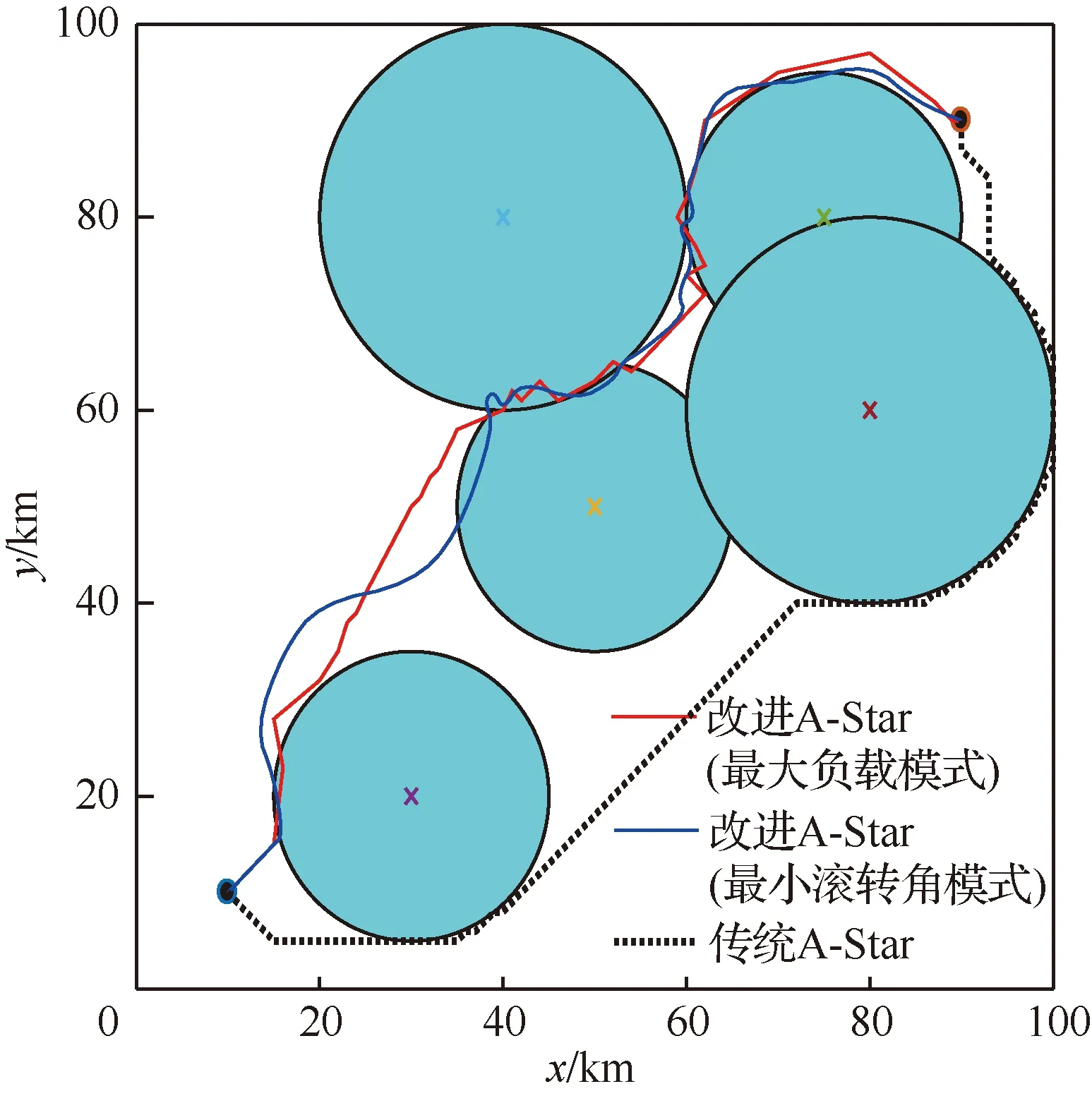
3.2 组网雷达系统

4 结 论
