基于可靠性分析的立方星网络维护架构优化
2020-07-30符弘岚张皓高扬
符弘岚,张皓,高扬
1. 中国科学院 空间应用工程与技术中心,北京 100094 2. 中国科学院大学 计算机与控制学院,北京 100049
立方星是一种以1U (10 cm×10 cm×10 cm)为基本单元的可扩展小型卫星,与传统卫星相比其开发周期短且研制成本低[1-3]。立方星体积小重量轻,配备的传感器、执行机构等硬件精度差,需要设计专门的控制算法抵消低精度带来的定姿、控制误差[4],这导致立方星在功能上比不上大型卫星,因此在开发应用初期立方星主要用于技术验证和作为教育平台使用[5]。为了更好地发挥立方星的优势,人们使用大量立方星以较低成本形成分布式空间传感器网络,实现传统单个卫星无法实现的功能[5]。构建立方星星座以执行商业、科学、技术验证任务已经率先在近地轨道实现。例如,Planet Labs建立了由120多颗Dove卫星组成的星座[6]。喷气推进实验室(JPL)设计在低地球轨道(LEO)上部署雨立方星座(Raincube Constellation)形成空间雷达网络[7]。除了执行近地空间任务,立方星星座在辅助深空探测任务领域也具有巨大潜能。如Chen 等提出在地月L2点部署4颗立方星为月球背面的用户提供定位服务[8]。
立方星通常作为搭载载荷与其他主要载荷一同发射。到达预定轨道后,由部署系统利用弹簧机构弹射出去[9-10],发射和弹射过程的振动会影响立方星的功能而降低任务成功率,统计数据显示立方星失败任务中约20%发生在发射和部署阶段[11]。另外可以用软袋将立方星打包发射到天基平台,如国际空间站(ISS)上[12],等待部署命令。ISS作为立方星部署的中转站,可以降低立方星在发射过程中遭受的振动级别,提高任务成功率。
分布式立方星网络立方星数目多,相较于传统卫星星座呈现出新的特点,立方星的发射成功率、部署成功率、故障发生频率等不确定性都与传统卫星不同。截至2018年5月31日,总的立方星任务失败率仍有25%,且立方星在早期运行阶段易发生故障的状况仍未得到明显改善[11]。传统的卫星星座(如导航卫星星座、通信卫星星座、遥感卫星星座)一般会有备份星,在部分卫星失效后启动,代替故障卫星工作[13-16]。对于分布式立方星网络,相较于直接从地面发射新的立方星,在轨道上储存备用立方星可以提高系统对故障的响应性[14]。传统备份星一般直接被部署于空间轨道,但是立方星更易受到恶劣空间环境的影响,直接暴露于轨道上会降低其寿命而影响备份效果,因此考虑使用在轨仓库储存备份立方星。在轨仓库与运载火箭、服务航天器、备用立方星组成在轨维护架构。然而由于立方星故障随机发生,用于维护立方星网络的备用立方星的需求不确定,在轨仓库应提前存储多少备用立方星难以确定。此外备用立方星还应适时从地面补充。因此,一个重要的问题是确定备用立方星的发射频率和发射数量,从而在保证系统性能的同时,降低维护架构的运行成本。由于故障的随机性,这个问题具有极大的挑战性。
Gu等提出基于航空部件寿命分布的部件采购策略以处理部件需求的不确定性,并且假定部件寿命服从正态分布[17]。Du Jonchay和Ho描述了一种由运载火箭、机器人服务设备和轨道仓库组成的机器人在轨服务基础设施,这篇文章假定故障发生服从泊松过程[14]。然而航天器故障行为并不一定遵守正态分布或者泊松过程[18],真实的模型应该来自真实的数据。部分学者对小卫星数据进行统计分析,结果表明Weibull分布适合用于建模卫星以及卫星子系统的故障行为[19]。
本工作旨在为维护架构优化提供更实际的解决方案,考虑随机故障行为,优化备用立方星的补给时刻和补给量,以降低维护架构的运行成本。提出了分布式立方星网络维护架构成本模型。接着收集了立方星故障数据,设计了最大化拟合优度参数估计方法,比较了不同分布类型对故障数据的拟合效果,最终选择Weibull分布来建模立方星的寿命分布[19-21]。最后结合成本模型和寿命分布模型采用蒙特卡罗仿真和遗传算法分析了成本模型参数对最优补给策略的影响。
1 维护架构与成本模型
1.1 维护架构
在合适时刻发射备用立方星替换故障立方星可以对立方星网络进行维护。分布式立方星网络维护架构如图1所示,由4部分组成:运载火箭、在轨立方星仓库、服务航天器和备用立方星(包括地面备份和在轨备份)。该架构进行维护的过程如下:一定数量的备用立方星适时搭载运载火箭到达在轨仓库,当立方星网络中有立方星发生故障时,由停靠于在轨仓库的服务航天器携带备用立方星/或者立方星采用自身的轨道机动系统转移至故障立方星的轨道,替换掉故障立方星,然后服务航天器返回在轨仓库,等待下次任务。

图1 立方星网络维护架构Fig.1 Maintenance architecture of CubeSat networks
使用在轨仓库临时存储备用立方星有两点优势:① 当网络损失立方星后,在轨仓库可以迅速释放备用立方星,对故障的响应性高;② 在轨仓库可以提供相对稳定的储存环境,降低恶劣的空间环境对备用星的影响,提高立方星的寿命。
1.2 成本模型
假定立方星网络维护架构的运行成本包括3部 分:固定成本、储存成本和短缺成本[17]。固定成本是指设计和制造立方星的成本;储存成本是用于为在轨仓库中的备用立方星提供稳定的储存环境所产生的成本;短缺成本是指空间传感器网络由于未能及时补充立方星而造成的经济损失。为了简化分析,本文不考虑地面备份、运载火箭发射成功率和备用立方星轨道转移成功率、备用立方星从在轨仓库转移到目标位置所消耗的时间。
成本模型用到的记号如下:s为单位时间短缺成本;h为单位时间储存成本;c为立方星的固定成本;T为规划周期;t为备用立方星到达在轨仓库时刻;Q为到达在轨仓库的备用立方星数量;n为故障立方星数量;j为t时刻前故障立方星总数量;tj为第j个故障发生时刻;tk为第k个故障发生时刻。
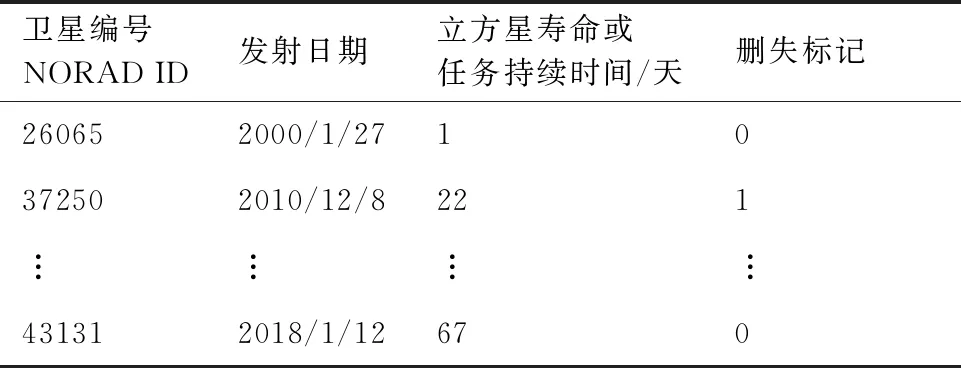
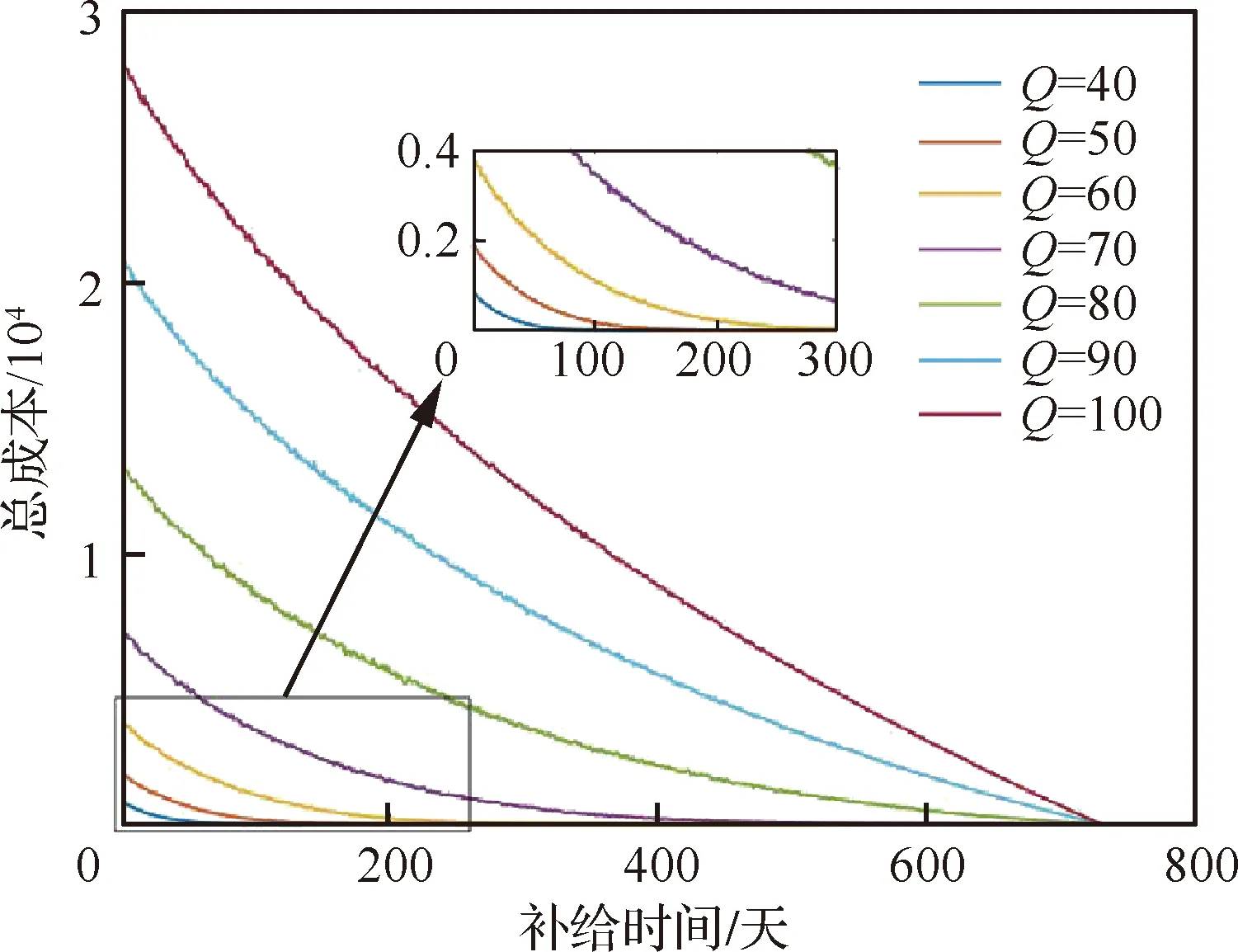
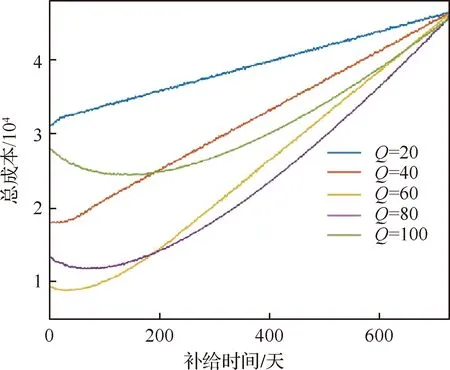
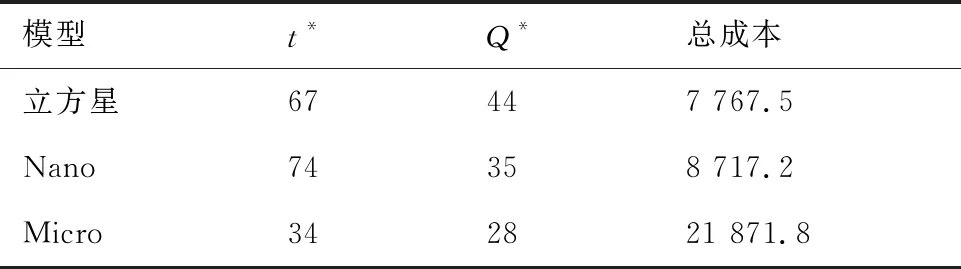
假定新的立方星在t时刻到达在轨仓库,tj≤t≤tj+1。同时假定在一个规划周期内共有n颗立方星发生故障。成本模型可以根据Q与j的大小分成5种情况(Q 图2 成本计算示意图(j+1 假设Q颗备用立方星在t时刻到达在轨仓库。其中j颗立即用于替换故障立方星。剩余的Q-j颗备用立方星从t时刻起被储存在在轨仓库中。每出现一个新的故障事件就消耗1颗备用立方星,直到第Q个故障发生并消耗掉最后一颗备用立方星,相应的储存成本为:h(tk-t),k=j+1,j+2, …,Q;短缺成本为:s(t-tk),k=1, 2, …,j。在这之后发生故障的n-Q颗立方星因为缺少备用立方星无法被替换,相应的短缺成本:s(T-tk),k=Q+1,Q+2, …,n。此种情况的总成本计算公式为 (1) 另外4种情况总成本分析方法与第4种情况类似,不再赘述。总的成本模型可统一写为 M= (2) 可靠性分析方法包括非参数分析方法和参数分析方法。非参数分析不需要假定寿命服从某一分布,适合于不同类型的故障数据,也可以用于评估参数分析的结果。参数分析首先假定寿命服从某一分布,然后估计该分布的参数。 由于立方星网络维护架构成本分析需要考虑立方星的寿命分布,因此本文选择参数分析方法,并用非参数分析方法评估参数估计结果。 收集了立方星寿命数据,包括立方星的发射时刻、故障发生时刻或项目结束时刻等[22]。如果立方星一直正常工作到任务完成,即没有故障发生,这样的数据称为右删失数据。本文获得的数据包含右删失数据。 由于一些立方星没有公开任务运行状态,最终共收集到111个有效数据,包括84个故障数据,27个删失数据,数据时间跨度为2000—2018年,足以进行统计分析并用于拟合参数模型。用于可靠性分析的数据示例如表1所示,其中删失标记0表示故障,1表示删失。 表1 立方星寿命数据示例Table 1 Lifetime data of CubeSats Kaplan-Meier(KM)估计方法可以从包含删失数据的故障数据中推导出经验可靠性函数。可靠性函数又称为生存函数,对于立方星而言,其可靠性函数表示立方星故障发生在t时刻之后的概率,计算公式为 (3) 式中:ti为故障时刻;ai为ti时刻故障立方星总数量;ni为ti时刻前正常运行的立方星数量,等于立方星总数量减去ti时刻前完成在轨任务的立方星数量(删失数量)和故障立方星数量。 该可靠性函数是阶梯状函数,在观察到的故障时刻处不连续,在删失时刻函数值不变。 参数分析首先需要选择合适的模型,然后采用参数估计算法估计模型参数。对数正态分布适合用于建模故障率随时间先增加后降低的对象的寿命分布,Weibull分布可以用于建模故障率随时间降低、增加、或不变的对象的寿命分布[21]。采用最大化拟合优度估计上述分布的参数。 1) 最大化拟合优度参数估计方法 统计模型的拟合优度表明观测数据与模型预测值的差异,拟合优度函数值越大表明模型拟合效果越好[19],因此可以对拟合优度函数进行优化,确定模型参数值。 对实际观测故障数据进行非参数分析得到的可靠性记为R(ti),由参数模型得到的可靠性记为R′(ti,α),α为模型参数,则拟合优度R2计算公式为 (4) (5) (6) (7) 最大化拟合优度参数估计建模为 α*=arg maxR2(α) (8) 采用遗传算法对式(8)进行求解。 2) 对数正态分布 假定立方星寿命x服从对数正态分布,即lnx~N(μ,σ2),则立方星的可靠性函数为 (9) 式中:erf为误差函数。 3) Weibull分布 Weibull分布广泛应用于可靠性分析中,能灵活描述不同故障行为,其PDF和CDF分别为 f(x;β,η)= (10) F(x;β,η)=1-exp(-(x/η)β) (11) 式中:β为形状参数;η为尺度参数。 假定立方星寿命x服从Weibull分布,则立方星的可靠性函数为 (12) 由1.2节分析可知,分布式立方星网络维护架构运行成本与立方星的故障时间序列、备用立方星的发射时刻和补给数量有关。因此分析成本模型首先需要生成故障时间序列。以两年(730天)为一个规划周期T,假定分布式网络由Qm颗相同的立方星构成,用Weibull寿命分布模型生成Qm个随机数,用以代表这Qm颗立方星的寿命,删除大于730的数,将剩余的随机数从小到大排序, 即为一个规划周期内的故障时间序列,记作{t}。 将故障时间序列,备用立方星补给时刻、补给数量代入式(2),可得到维护架构的运行成本。但是由于故障时刻是随机的,单个故障时间序列对应的总成本随着补给时刻延后而波动变化,因此采用蒙特卡罗仿真,求N个故障时间序列对应成本的平均值对成本进行分析。 为了求解最小总成本对应的最优补给策略,给出优化模型。采用遗传算法求解可得到最优补给时刻t*和最优补给数量Q*,即 (13) 式中:{t}l表示第l个故障时间序列。 采用最大化拟合优度方法分别估计了对数正态分布和Weibull分布的参数,同时对比文献[19] 中结合马尔可夫链-蒙特卡罗(MCMC)仿真的贝叶斯方法,对比了这2种参数估计算法对于立方星故障数据的拟合效果。 非参数分析方法Kaplan-Meier估计得到立方星的可靠性如图3中的阶梯状曲线所示,可以看出立方星可靠性在初期迅速降低,随后缓慢降低。 图3 不同参数估计方法对比Fig.3 Contrast of different parameter estimation methods 参数估计结果列于表2。拟合优度R2越接近于1说明拟合优度越好。对于Weibull分布,最大化拟合优度参数估计方法所得结果的R2比MCMC方法所得结果的R2更大,说明前者的拟合效果更好。如图3所示,在早期,最大化拟合优度参数估计方法获得的可靠性函数曲线显然更靠近KM非参数分析得到的曲线,即该方法能更好地拟合立方星的早期失效率高的特征,也说明了最大化拟合优度参数估计方法拟合精度更高。Weibull分布拟合结果的R2大于对数正态分布拟合结果的R2,说明Weibull分布更适合用于立方星寿命分布的拟合。 表2 参数估计结果Table 2 Parameter estimation results 下面分析最大拟合优度方法Weibull分布拟合结果。β=0.476 8,β<1,表明立方星具有早期失效率高的特点。η=291.900 4,表示立方星的特征寿命为291.900 4天。当t=η时,代入Weibull分布的累计分布函数(CFD),得到F(t)=0.632,表示当立方星网络运行到第291.900 4天时,可能有63.2%的立方星发生故障。 早期立方星主要用于技术验证或科学实验,因此收集的故障数据前一部分以验证或实验立方星为主。随着技术发展,执行商业任务的业务立方星出现[6],对可靠性要求更高。有必要将数据按发射时间等分成早期和近期两部分,分别进行参数估计,得到两类可靠性,结果如表3和图4所示。由表3可知,近期发射的立方星的特征寿命约为415 天,明显高于早期发射的立方星,但是形状参数β差别不大,都呈现出早期失效的特点;由图4 可知近期发射的立方星的可靠性也高于早期的立方星。该对比在一定程度上说明了验证实验立方星与业务立方星的差异性,因此在优化业务立方星网络补给策略时,需要考虑这种差异性。 表3 早期、近期数据参数估计结果 图4 早期、近期立方星对比Fig.4 Contrast of early and recent CubeSats 分布式立方星网络维护架构成本模型中有3个 未知参数:c、h、s,通过调节这些参数的大小,可以涵盖大多数的情形。假定立方星网络由100颗 立方星组成,分析这3个参数对总成本的影响。 1) 单一成本情况 只考虑固定成本,即c:h:s=1:0:0时,成本模型简化为:M=cQ,总成本与补给时刻无关,仅与补给数量成正比。 只考虑储存成本,即c:h:s=0:1:0时,t、Q对总成本的影响如图5所示,总成本随着补给时刻延后而降低,随着补给数量增加而增加。值得注意的是,当补给数量小于60,补给时刻延后至第300天之后时,储存成本降为零,原因如下:由Weibull分布拟合结果可知立方星的特征寿命约292天,表示当立方星网络运行到第292天时,可能有63.2%的立方星发生故障;立方星网络由100颗立方星组成,当运行到292天时,可能有63颗 立方星发生故障,因此在第300天之后补给立方星数量小于60时,这些补给的立方星将全部立即用于替代故障立方星,因此总储存成本为零。 图5 储存成本对总成本的影响(c∶h∶s=0∶1∶0)Fig.5 Effect of holding costs on total costs (c∶h∶s=0∶1∶0) 只考虑短缺成本,即c∶h∶s=0∶0∶1时,t、Q对总成本的影响如图6所示,总成本随着补给时刻延后而增加,随着补给数量增加而降低。当补给数量超过80时,改变补给数量,总成本随补给时间的变化曲线几乎重合(如图6放大图所示,Q=90与Q=100的曲线几乎是重合的),这是由于在规划周期内,总故障立方星数目小于80的概率非常大,补给立方星数目大于80时,所有故障立方星都能被替换,因此总的累积短缺时间是相同的,又由于没有考虑短缺成本和固定成本,所以总成本相同。 图6 短缺成本对总成本的影响(c∶h∶s=0∶0∶1)Fig.6 Effect of shortage costs on total costs (c∶h∶s=0∶0∶1) 2) 全部成本情况 同时考虑固定成本、储存成本、短缺成本,即取c∶h∶s=1∶1∶1时,t、Q对总成本的影响如图7所示。补给数量较少(大约是Q≤60)与补给数量较多时对总成本的影响存在较大差异:当补给数量较少时,总成本随着补给数量增加而减少,随着补给时刻延后而增加;当补给数量较多时,总成本随着补给数量增加而增加,随着补给时刻延后先降低后增加。这一差异反应了短缺成本和储存成本对于总成本不同影响效果,这2种成本分别对应备件短缺和备件冗余2种情况。 图7 3种成本参数对总成本的影响(c∶h∶s=1∶1∶1)Fig.7 Effect of three cost parameters on total costs (c∶h∶s=1∶1∶1) 由上述分析可得出下述结论:只考虑储存成本,补给时刻取在立方星的特征寿命292天之后,补给数量小于网络中立方星总量的63.2%时,总储存成本为0;只考虑短缺成本,当补给数量Q>80时,总成本不再随着补给数量增加而变化。当补给数量较少时,短缺成本对总成本的影响占主导;当补给数量较多时,储存成本对总成本的影响占主导。 分析不同成本比例对于最优补给策略的影响,这里的不同比例指短缺成本与储存成本的不同比例,由于立方星成本正在逐步降低,因此暂不考虑固定成本,最优补给策略指最优补给时刻t*、最优补给数量Q*;并且对比了立方星网络不同规模的仿真结果,考虑网络中立方星数量分别为50、100、150这3种情况。 如图8所示,随着s/h比例增大,最优补给时刻均提前,但最优补给时刻与立方星网络规模无关,都没有超过150天,均在规划早期取得,这与立方星的故障行为有关,由4.1节分析可知立方星有早期失效特点,即立方星在轨运行早期发生故障的概率较高,因此在轨运行早期发生故障的立方星数目比在轨运行中期和后期的故障数目要多,所以应该在早期及时补给备用立方星。 图8 s/h对t*的影响(不考虑固定成本)Fig.8 Influence of s/h on t* (without considering fixed costs) 如图9所示,考虑不同比例的s/h,立方星网络最优补给数量大小与规模正相关且变化趋势相同,随着短缺成本所占比重增加,最优补给数量也随之增加,这是由于增大补给数量能够缓解备件短缺情况。 图9 s/h对Q*的影响(不考虑固定成本)Fig.9 Influence of s/h on Q* (without considering fixed costs) 将由故障数据和最大化拟合优度方法得到的可靠性模型和文献[19]中的与立方星质量相接近的Nano卫星、Micro卫星的可靠性模型(如表4所示)分别代入到维护架构补给策略优化模型中,得到3种补给策略,依次记为立方星模型Nano模型、Micro模型;再将3种补给策略和基于数据的可靠性模型代入维护架构,计算总成本。结果如表5所示。 表4 文献[19]模型参数Table 4 Model parameters of Ref.[19] 表5 不同补给策略比较Table 5 Contrast of different supply strategies Nano模型与立方星模型的结果接近,总成本增加了12.23%;而Micro模型相对于立方星模型结果总成本增加了181.58%。这说明引入适当的实际故障数据对维护架构进行优化的必要性。 由于早期和近期发射的立方星均具有早期失效的特点,都应该在规划早期补给备用立方星,因此只对补给数量进行对比分析。用早期和近期的立方星可靠性模型,分别求解由100颗立方星组成的网络的最优补给数量。如图10所示,对于不同成本比例,近期立方星的补给数量均小于早期立方星的补给数量。由4.1节分析可知,近期发射的立方星的可靠性更高,因此在规划周期内立方星网络中发生故障的立方星数量相对更少,所以需要的补给量也少。这一结论说明在优化立方星网络的维护策略时,应该考虑技术发展导致的可靠性模型的变化。 图10 早期、近期立方星Q*对比Fig.10 Q* comparison between early and recent CubeSats 1) 立方星寿命分布的参数模型可采用Weibull分布或对数正态分布,进而采用最大化拟合优度参数估计方法进行参数估计,拟合数据表明Weibull模型精度比对数正态分布模型稍高。 2) 立方星具有早期失效率高的特点,由于这一特点,备用立方星最优补给时刻建议为规划周期早期。目前立方星总的特征寿命大约为292天,近期发射的立方星的可靠性高于早期发射的立方星。 3) 基于本文收集的立方星寿命数据,若在轨服务成本以短缺成本为主,那么建议备用立方星补给时间不晚于第150天,补给数量与立方星网络规模有关。若以储存成本为主,建议备用立方星补给数量约等于立方星网络中立方星总数量的60%,补给时刻不晚于第300天。补给时刻随短缺成本/储存成本增加而提前,与立方星网络规模无明显相关关系;补给数量随短缺成本/储存成本增加而增加。 4) 近期发射立方星的最优补给数量比早期立方星的少,对立方星网络的补给策略进行优化时,不仅需要选择合适的可靠性模型,还需要考虑由于技术发展而导致的立方星可靠性模型的变化。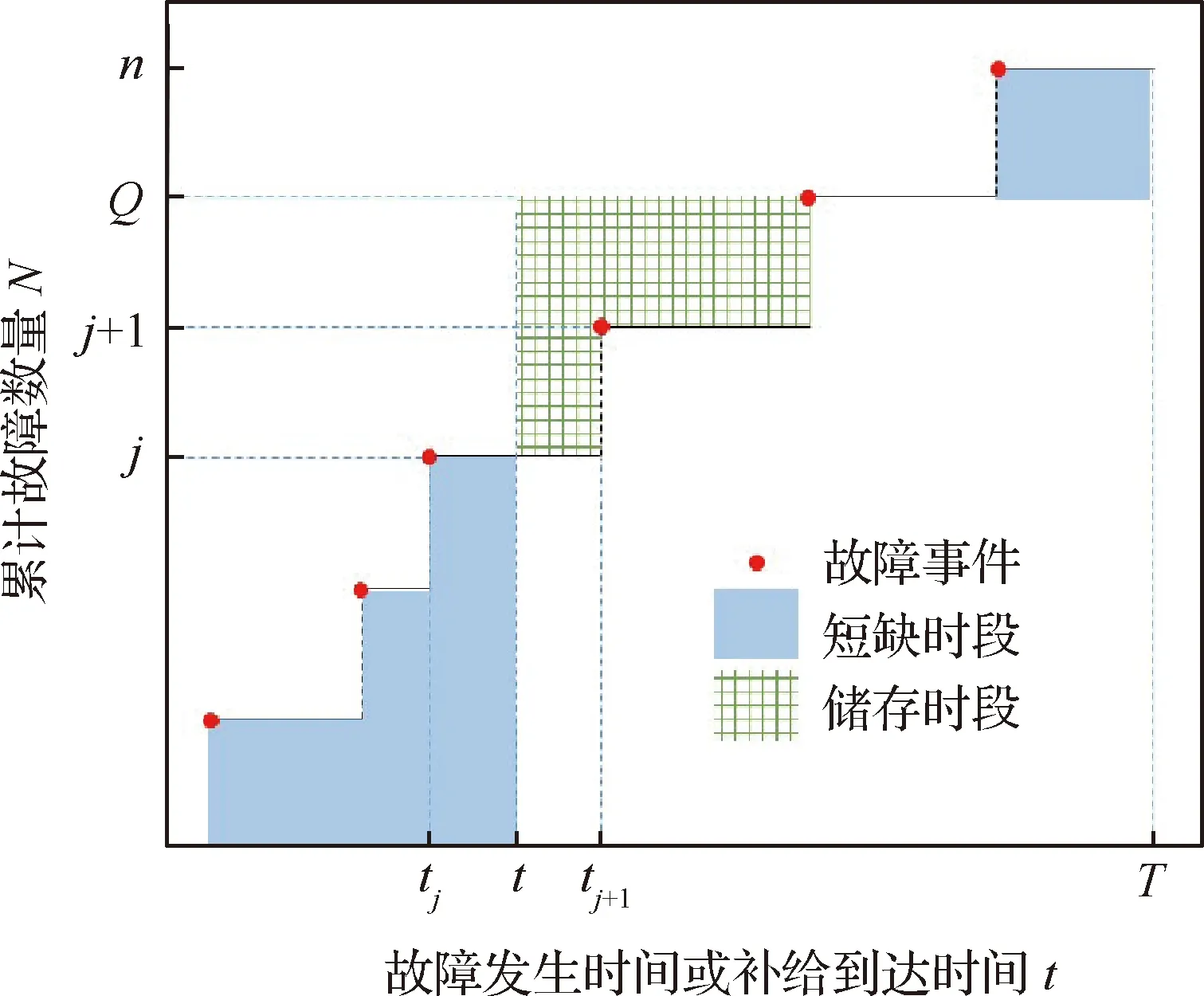
2 立方星可靠性模型
2.1 立方星寿命数据
2.2 非参数分析
2.3 参数分析


3 仿真方法

4 结果分析
4.1 立方星寿命分布模型




4.2 参数对总成本的影响

4.3 最优补给时刻与最优补给数量


4.4 不同可靠性模型对应的成本比较

4.5 早期、近期立方星补给策略对比

5 结 论
