基于IPSO-Elman神经网络的飞机客舱能耗预测
2020-07-30林家泉孙凤山李亚冲庄子波
林家泉,孙凤山,李亚冲,庄子波
1. 中国民航大学 电子信息与自动化学院,天津 300300 2. 中国民航大学 飞行学院,天津 300300
随着节能减排的规划逐步推进,民航设备的节能减排也受到越来越多的关注。在夏季,飞机停靠在机场时,大部分航空公司均采用飞机地面空调设备为客舱制冷[1],准确预测出客舱的能耗需求,是达到地面空调节能以及保证客舱热舒适性的关键,也有助于机场电能的合理分配。同时,由于地面空调采用恒速的送风策略,当地面空调送风速度过小时,不满足客舱热舒适性要求,当地面空调送风速度过大时,浪费能源。因此,若能准确地预测客舱的能耗,通过计算能够得出既满足热舒适性又节能的地面空调的最优送风速度,则能为地面空调的送风控制提供理论依据。地面空调为客舱制冷如图1所示。影响客舱能耗的主要因素为天气因素与客舱内部因素,天气因素主要包括室外温度、湿度、太阳辐射强度、降水量等,客舱内部因素主要包括客舱内的温度、湿度、风速等[2]。

图1 地面空调系统Fig.1 Ground air condition system
人工神经网络方法广泛地运用于建立非线性数据间的关系,以达到预测的目的[3]。文献[4]提出基于改进的遗传算法用于优化极限学习机网络的航空发动机轴承故障预测模型,文献[5]提出将人工神经网络运用于建筑物能耗预测中,取得了较为理想的效果。文献[6]提出基于小波神经网络,运用于飞机客舱能耗预测中,建立了飞机客舱能耗预测模型。综上可知,由于影响客舱能耗的因素间也存在着这种非线性特性,在采集到的样本数据充足的情况下,依据神经网络建立客舱能耗预测模型理论上是可行的。
Elman神经网络采用梯度下降的学习规则,存在容易陷入局部最优且收敛速度慢的问题。有学者提出使用标准的粒子群优化(PSO)算法优化Elman神经网络[7],但实验结果显示,基于标准的PSO优化后的Elman神经网络,仍然存在精度不佳的问题。因此,需要对PSO算法进行改进。改进PSO算法能够通过调节算法的惯性权重与学习因子实现。文献[8]通过调节PSO算法中的学习因子c1和c2,c1随着迭代次数的增加进行线性递减变化,c2随着迭代次数的增加进行线性递增变化,增强了算法搜索能力,使得寻优精度得到提高。文献[9]提出一种惯性权重的非线性递减调节,加快了算法的寻优速度。文献[10]提出了一种基于全局最优位置对惯性权重进行动态调节的方法,改进了PSO算法。文献[11]提出了一种基于粒子聚集程度的惯性权重动态调节方式,在一定程度上避免了算法陷入局部最优。文献[12]通过结合粒子的适应度对惯性权重进行动态调节,提高了算法的精度。
仅单一调节学习因子或惯性权重,并未考虑惯性权重与学习因子之间的配合作用,则不能建立粒子的局部搜索能力与全局搜索能力的动态平衡[13]。因此,为使得PSO算法得到更大程度的优化,本文考虑了2个参数之间的配合,基于参数的收敛域,提出了基于粒子到全局最优位置的距离对惯性权重与学习因子进行动态调节,构造了两者的动态调节函数,同时,引入了变异因子,提出了跳出局部最优的策略,避免PSO算法过早收敛,使得PSO算法得到改进,提高了PSO算法的收敛速度与精度。将IPSO算法与Elman神经网络相结合,通过IPSO算法的全局最优位置对Elman神经网络的权值与阈值进行更新,将IPSO-Elman应用于对Boeing738飞机客舱进行能耗预测,用以准确预测出飞机客舱的能耗并缩短预测耗时。
1 Elman神经网络和PSO算法
1.1 Elman神经网络
Elman神经网络是在BP(Back Propagation)神经网络上增加一个承接层使得网络对历史数据具有短期记忆功能,增强了其处理动态数据的能力[14]。Elman神经网络结构如图2所示。
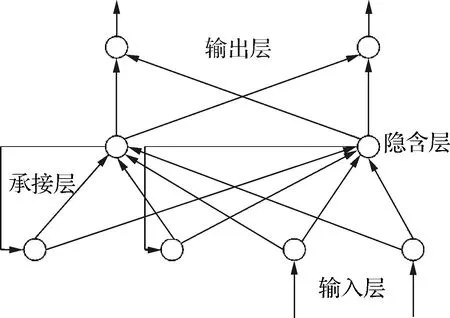
图2 Elman神经网络结构Fig.2 Structure of Elman neural network
Elman神经网络的模型为
xc(t)=axc(t-1)-x(t-1)
(1)
x(t)=g(W1xc(t)+W2u(t-1))
(2)
y(t)=f(x(t)W3)
(3)
式中:u(t-1)为神经网络的输入;x(t)为隐含层输出;xc(t)为隐含层向承接层的输入;W1、W2、W3分别为承接层到隐含层、输入层到隐含层、隐含层到输出层的权值;t表示迭代计算到第t步;y(t) 为神经网络输出;g(*)为隐含层传递函数;f(*)为输出神经元的激励函数。
Elman神经网络的误差函数为
(4)
式中:ei(t)为期望输出;m为样本总数;i为第i个样本。
1.2 PSO算法
PSO算法受鸟群搜寻食物行为的影响而产生[15],影响鸟群中的鸟搜寻食物主要有2个因素:鸟飞行的速度、鸟和食物之间的距离。同样,将鸟群中的鸟视为粒子群中的粒子,搜寻食物的过程视为粒子搜寻最优解的过程。
每一个粒子均有速度和位置2个属性,在每次迭代计算中,每个粒子在K维空间下,以一定的速度和位置在搜寻最优解,将搜寻到自己的最优解所处位置记为个体极值,其中Vi={Vi1,Vi2,…,Vik}为第i个粒子速度,xi={xi1,xi2,…,xik}为第i个粒子位置,Pbesti={Pbesti1,Pbesti2,…,Pbestik}为第i个粒子的个体极值。
假设目标函数为fg(x),第i个个体极值的计算式为[16]
Pbesti=
(5)
将个体极值与粒子群中的其他极值共享,选出最优的个体极值做为全局最优位置gbest(t)。假设粒子群中含有N个粒子,迭代次数为t,gbest(t)的求解过程为
Gbest(t)=min{fg(Pbest 1(t)),fg(Pbest2(t)),…,
fg(Pbest N(t))}
(6)
若fg(Pbesti(t))=Gbest(t),则有gbest(t)=Pbestj(t),Gbest(t)为全局最优位置对应的适应度函数值。
每个粒子通过全局最优位置来调整其位置和速度。粒子的速度与位置计算公式为
Vij(t+1)=ωVij(t)+c1r1[Pbest ij(t)-xij(t)]+
c2r2[gbest j(t)-xij(t)]
(7)
xij(t+1)=xij(t)+Vij(t+1)
(8)
式中:i为粒子群的粒子个数,i=1,2,…,N;j为搜索空间的维数,j=1,2,…,K;Vij(t)为迭代t次后,粒子的速度;xij(t)为迭代t次后,粒子所在的位置;Pbest ij为第i个粒子的个体极值的j维值;gbest j为全局最优位置的j维值;r1与r2为[0,1]上的随机数;c1、c2为学习因子;ω为惯性权重。
2 IPSO算法优化Elman神经网络
2.1 粒子与全局最优间的距离
PSO算法中,粒子的位置更新与速度更新取决于全局最优位置,当粒子与全局最优位置的距离较大时,粒子分布分散,有助于粒子的全局搜索,粒子分布集中,有助于粒子的局部搜索。因此,粒子与全局最优位置之间的距离是学习因子与惯性权重动态调节过程中的重要因素,在第t次迭代中,每个粒子与当前全局最优位置之间的距离R(t)的计算公式为
R(t)=
(9)
2.2 基于R(t)的惯性权重及学习因子动态调节
单一调节粒子群的惯性权重或学习因子,很难使粒子群算法达到最佳效果,需要进行惯性权重与学习因子的共同调节。
在PSO算法中惯性权重ω影响了粒子群的粒子搜索能力,当ω较大时,全局搜索能力强,更容易定位到全局最优解的大体位置,ω较小时,局部搜索能力强,更容易逼近全局最优解。研究结果表明对惯性权重随着迭代次数的增加进行递减的动态调节方式有助于加快算法的收敛速度与提升精度[17]。为了进一步改善PSO算法的收敛速度与精度,引入每个粒子与当前全局最优位置之间的距离R(t),即第t次迭代中,每个粒子与当前全局最优位置之间的距离R(t)。利用R(t)在寻优前期较大、在寻优后期较小的特点,提出了一种结合R(t)、ω随着迭代次数的增加进行非线性递减的动态调节方法,使ω在迭代寻优的前期拥有较大的值,快速最优解的位置,使ω在迭代寻优的后期,拥有较小的值,更快逼近最优解,所构造的ω动态调节函数如式(10)所示,对ω的动态调节过程如图3所示。本文ω的取值范围为[0.4,0.9][18]。
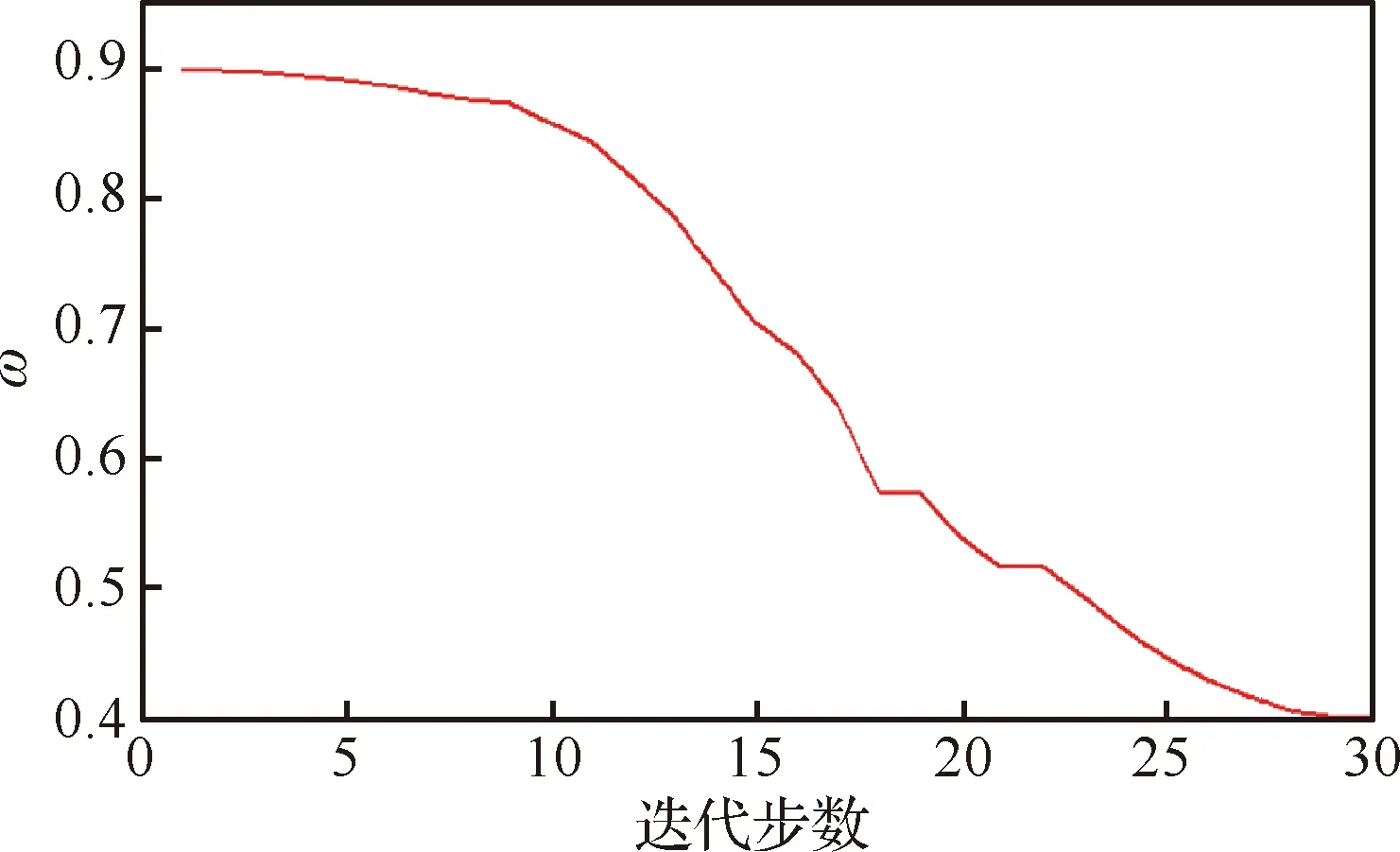
图3 惯性权重调节过程Fig.3 Adjustment process of inertia weight
ω(t)=ωmin+(ωmax-ωmin)·
(10)
式中:tmax为t的最大迭代次数;ωmax为惯性权重的最大值;ωmin为惯性权重的最小值;Rmax为粒子与全局最优位置的距离最大值;ω(t)为第t步惯性权重的值。
在PSO算法中学习因子c1、c2影响了粒子群中粒子寻找最优解的运动轨迹,c1决定粒子的个体认知能力,c1取值越大算法搜索全局最优解越依靠个体极值,c2决定粒子的社会认知能力,c2取值越大算法搜索全局最优解越依靠群体最优位置。利用R(t)在寻优前期较大、在寻优后期较小的特点,提出了一种结合R(t)、c1随着迭代次数的增加进行非线性递减的动态调节方法,一种结合R(t)、c2随着迭代次数的增加进行非线性递增的动态调节方法。所构造的c1、c2的动态调节函数如式(11)和式(12)所示,c1、c2的动态调节过程如图4所示。

图4 学习因子调节过程Fig.4 Adjustment process of learning factors
c1(t)=c1min+(c1max-c1min)·
(11)
c2(t)=2.8-c1(t)
(12)
式中:c1min为学习因子c1的最小值;c1max为学习因子c1的最大值;c2min为学习因子c2的最小值;c2max为学习因子c2的最大值;c1(t)为第t步学习因子c1的值;c2(t)为第t步学习因子c2的值。
根据文献[15]得出了PSO算法的ω与c1、c2的收敛域,其中0 为了避免PSO算法的过早收敛现象,提出了一种跳出局部最优的策略。依据遗传算法中的变异思想,引入了变异因子,通过分析粒子的聚集程度与变异因子的关系,构造了全局位置的更新函数,使得算法跳出局部最优。聚集程度的判定公式为[19] (13) 式中:N为粒子群中粒子的个数;,fi为第i个粒子的适应度;favg为当前粒子群的平均适应度;σ2为粒子群的聚散程度;n为归一化定标因子。 设定变异因子s的值为0.1,迭代计算至第t步,当σ2 gbest(t)=gbest(t)(σ2r+1) (14) 式中:r为[0,1]之间的随机数。 利用IPSO算法得到的全局最优位置作为Elman算法的最优权值与阈值,使得Elman神经网络得到优化,IPSO-Elman的流程图如图5所示。IPSO-Elman神经网络的步骤如下: 图5 IPSO-Elman算法流程图Fig.5 Flow chart of IPSO-Elman algorithm 1) 样本数据归一化,确定Elman神经网络的网络结构,建立Elman神经网络。 2) 初始化粒子的速度、位置、惯性权重、加速因子及迭代次数。 3) 计算粒子的适应度,粒子的适应度定义为 (15) 4) 根据粒子的适应度值求得个体最优位置与全局最优位置。 5) 计算粒子群的聚集程度,若聚集程度的值小于变异因子的值,则根据式(14)更新当前全局最优位置,否则不对当前全局最优位置进行改变。 6) 根据式(10)~式(12)对学习因子与惯性权重进行动态调节,避免PSO陷入局部最优,加快算法迭代速度。 7) 判断粒子适应度是否小于设定值或达到最大迭代次数,满足条件,则退出PSO算法,否则返回步骤3),继续计算粒子适应度。 8) 依据Elman神经网络的网络结构,将IPSO得到的全局最优位置分配给Elman神经网络作为其最优阈值与最优权值,利用样本数据进行网格训练。 9) 当网格训练的误差小于设定值时,结束训练,对测试数据进行仿真。 为了达到客舱能耗预测的目的,需要建立影响客舱热舒适性的主要因素与客舱能耗之间的关系,影响客舱热舒适性的主要因素为客舱温度与湿度[20]。因此,为建立飞机客舱能耗的预测模型,采集了夏季停靠在某机场,使用地面空调制冷的Boeing738飞机客舱能耗数据,包括乘客下机后的客舱温度和湿度,乘客登机时到达客舱热舒适性要求的客舱温度和湿度以及飞机客舱的耗电量。研究飞机客舱能耗的阶段为当上一批乘客下机完成,使用地面空调对飞机客舱进行制冷,在下一批乘客登机时为止。共采集300组能耗数据,部分采集数据如表1所示。 表1 部分样本数据Table 1 Part of sample data 为消除样本数据中奇异样本数据的影响,需要对样本数据进行归一化: (16) 式中:dmax与dmin为样本数据中的最大值与最小值;d′为归一化后的样本数据。 Elman神经网络是在BP神经网络上增加了一个承接层,以达到记忆的目的,使得其对历史数据更加敏感,相比于BP神经网络具有更强的计算能力,而能耗预测模型的训练与验证依靠历史数据。因此,为准确预测出客舱能耗,选择Elman神经网络建立飞机客舱能耗预测模型。在获取了实验数据后,需要建立能够用于研究实验数据的神经网络。由于地面空调能耗产生的原因是为客舱制冷除湿,以达到乘客的热舒适性要求,而影响客舱热舒适性的主要因素为温度与湿度,两者具有较强的耦合性且对于客舱能耗的影响较大,故选择乘客下机后的客舱的温度和湿度,乘客登机时达到客舱热舒适性要求的客舱温度和湿度作为预测模型的输入数据,飞机客舱的能耗量为输出数据。共计4种输入数据、1种输出数据,因此,得出Elman神经网络的输入层为4个节点,输出层成为1个节点,隐含层节点数的计算公式为[21] (17) 式中:min为输入层节点数;nout为输出层节点数;a为0~9之间的常数。 为判断出H的取值对Elman神经网络性能的影响,得出H的最佳值,根据H的取值范围[3,12],建立了含有不同H的Elman神经网络。依据飞机客舱能耗的实验数据,进行50次仿真实验,每次仿真实验进行1 000次迭代运算,得出H值不同时Elman神经网络的平均误差,如表2所示。 由表2可知,当H=10时,Elman神经网络预测值与实际值的平均误差最小,故Elman神经网络隐含层的节点数H取10。同时,由于Elman神经网络承接层的节点数应该与隐含层一致,故承接层的节点数也为10。 表2 Elman神经网络的平均误差Table 2 Average error of Elman neural network 由于设定Elman神经网络的输入层节点数为4,隐含层节点为10,承接层节点数为10,输出层节点数为1。所以,IPSO的维数为161,粒子个数为[22] (18) 式中:D为IPSO的维数;int(·)为向下取整。 IPSO的维数为161,则存放全局最佳位置的矩阵为1×161。而Elman神经网络输入层到隐含层的权值矩阵为10×4的矩阵,共计40个权值,隐含层到承接层权值矩阵为10×10的矩阵,共计100个权值,隐含层的阈值矩阵为10×1的矩阵,共计10个阈值,隐含层到输出层的权值矩阵为1×10的矩阵,共计10个权值,输出层的阈值矩阵为1×1的矩阵,共计1个阈值。因此,将全局最优位置中的前40个元素分配作为神经网络输入层到隐含层的最优权值,第41~140个元素分配作为隐含层到承接层的最优权值,第141~150个元素分配作为神经网络隐含层的最优阈值,将第151~160个元素分配作为神经网络隐含层到输出层的最优权值,将第161个元素分配作为神经网络输出层的最优阈值。 为验证IPSO-Elman神经网络的预测精度以及收敛速度,进行了IPSO-Elman神经网络的编程,建立了Boeing738飞机客舱能耗预测模型。同时,与Elman神经网络、PSO-Elman神经网络进行对比。其中总的数据集为300组能耗数据,随机选择290组数据作为训练数据,验证数据为10组,利用该方法对模型进行了验证。设定粒子群个数为35,网络结构为4-10-10-1的Elman神经网络,PSO-Elman依据参数设定标准[23]设定学习因子c1为2.05、c2为0.5,每种方法均进行50次独立的仿真实验,每次仿真中IPSO算法进行200次迭代计算,Elman神经网络算法进行1 000 次迭代计算,以预测模型跳出局部最优所需要的迭代次数为评判收敛速度快慢的标准。以预测结果与真实值之间的相对误差的平均值作为模型精度优劣的评判指标,相对误差的计算公式为[24] (19) 式中:upi为第i个预测值;uti为第i个真实值。 在预测模型的训练函数、隐含层传递函数、输出层传递函数以及相对误差方面,对3种不同飞机客舱预测模型进行综合分析与对比,所得结果的比较如表3所示。其中常用的训练函数包括:traingd、trainlm、 traingda、traingdx,隐含层常用的传递函数包括:logsig、tansig、radbas、tribas。常用的输出层传递函数为purelin。 由表3能够得出,基于IPSO-Elman的飞机客舱能耗预测模型,选择训练函数为trianlm,传递函数为tansig、purelin时,其最小相对误差仅为0.06%,相比于其他2种预测模型,预测精度有了一定的提升。依据表3分析能够得出训练函数以及传递函数的选取极大地影响了预测结果,当基于IPSO-Elman的飞机客舱能耗预测模型选择训练函数为traingda,传递函数为radbas、purelin时,其最小相对误差为1.35%,预测误差大大提高,因此,使用神经网络对不同数据集进行预测研究时,分析出适合该数据集的训练函数与传递函数是至关重要的。同时,当训练函数选择traingd,传递函数选择radbas、purelin时,PSO-Elman能耗预测模型的预测精度不如Elman能耗预测模型,可知,由于PSO算法自身也存在着容易陷入局部最优的特点,导致标准的PSO优化Elman神经网络的效果不佳,因此,对标准PSO算法的改进很有必要。 表3 不同模型的预测结果对比Table 3 Predictive results comparison of different models 续表 当选择训练函数为trianlm,传递函数为tansig、purelin时,3个模型的预测结果对比如图6所示,从图中能够得出IPSO-Elman预测精度最高。 图6 模型的预测值与真实值对比Fig.6 Comparison of predicted and real values of model PSO-Elman与IPSO-Elman模型的收敛速度对比如图7所示,从图中能够看出IPSO-Elman的收敛速度明显加快。跳出局部最优的迭代步数与适应度函数的值如表4所示。 图7 收敛速度对比Fig.7 Comparison of convergence rates 由表4能够得出,基于IPSO-Elman的飞机客舱能耗预测模型,其达到适应度函数的稳定值的迭代步数为96步,稳定值的适应度函数值为53.03,相比于PSO-Elman预测模型,收敛速度有了一定的提升。可知,该预测模型考虑了学习因子与惯性权重之间的配合调节,同时,引入了变异因子,使得算法在收敛速度与精度上取得了提高。 表4 稳态步数与适应度函数值Table 4 Steady state steps and fitness function values 1) 为准确预测飞机客舱的能耗,通过考虑粒子与全局最优位置的距离并引入变异因子,提出了一种动态调节PSO中的学习因子与惯性权重的方法,构造了学习因子与惯性权重的动态调节函数与全局位置的更新函数,进而建立了IPSO算法。 2) 将IPSO与Elman算法结合,建立了IPSO-Elman的飞机客舱能耗预测模型。 3) 通过仿真验证了IPSO-Elman相比于Elman、PSO-Elman对飞机客舱能耗的预测,在预测精度与收敛速度方面均有一定程度的提高。 IPSO-Elman飞机客舱能耗预测模型在一定程度上解决了飞机客舱能耗预测的精度不高与收敛速度慢的问题,为飞机地面空调的能耗预测提供了支持。2.3 跳出局部最优的策略
2.4 IPSO-Elman神经网络
3 飞机客舱能耗预测
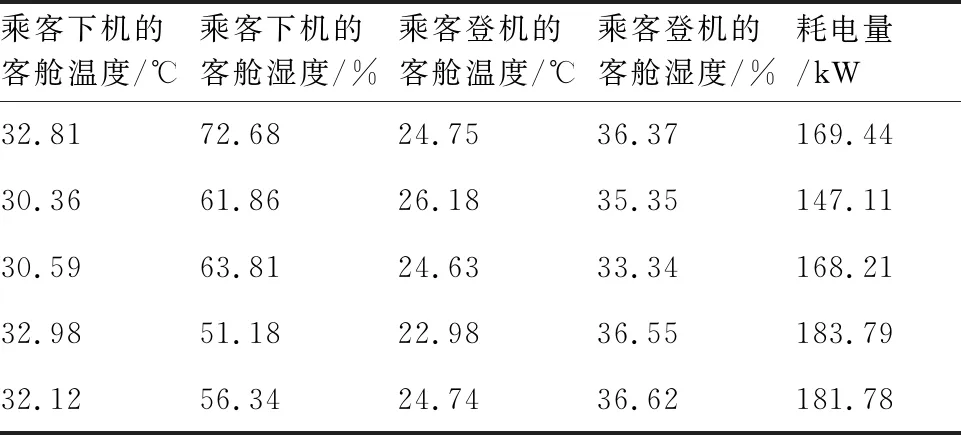
3.1 数据来源
3.2 数据归一化处理
3.3 Elman神经网络结构的建立

3.4 IPSO算法参数设置
3.5 Elman神经网络最优权值与阈值的获取
4 算法验证





5 结 论
