实测地质剖面中地层真厚度计算公式的修正

王兆国，鲁如魁，夏立元

（1. 西北大学大陆动力学国家重点实验室，陕西西安710069；2. 西北大学地质学系，陕西西安710069；3. 安徽省地质调查院，安徽合肥230001）

区域地质调查工作是获取野外第一手资料的主要手段，也是综合分析沉积相和古地理环境、厘定构造格架、重塑区域构造演化史等后续研究工作的重要基础，主要包括地质踏勘、实测剖面和地质填图等三阶段工作。实测地质剖面是厘定地层结构构造特征与地层接触关系、确定地质填图单元及其识别标志的核心工作，涉及剖面实测和编制综合地层柱状图两部分内容。近年来很多学者针对实测地质剖面的绘制问题进行了很多研究［1-3］，发展了新的地质剖面绘制方法［4-5］，并进行了数字化成图［6-9］、自动成图［10-11］和数据库系统建设［12-17］等研究工作。综合地层柱状图的编制涉及真厚度的计算问题，Mertie［18］和Price［19］分别提出了地层厚度计算公式，与20世纪50 年代引入我国的列氏厚度计算公式相同［20］，Ickes［21］给出了用积分和方向余弦表示的地层厚度公式，Price［22］指出用斜距（纵横距）、真倾角、坡角和地层倾向与测绳经过的坡向的夹角表示的地层厚度公式对于地质学家更适用，Mandelbaum等［23］指出公式存在负值问题，建议采用绝对值对负值进行处理，Addie［24］提出了用视倾角表示的地层厚度公式，对于负值依然采用取绝对值进行处理。列式公式引入我国后，为便于计算，前人对列氏公式进行了多次讨论和改进［25-28］，叶东虎［29］编著了岩层厚度计算手册，刘元生［30］设计绘制了地层厚度计算表盘，许边远［31］在对列氏公式进行改进的基础上，提出了正负厚度的概念，朱正勇等［32］根据计算结果针对不同的测量情况对列氏公式采用了取绝对值和负值的方式进行了改正。在上述文献中，特别是实际工作中发现有“0值”、“负值”现象，其产生的根源、“负值”和“负厚度”概念统一性问题、列氏公式适用性等问题悬而未决，亟待研究。

本文从实际工作过程中不同野外露头情况出发，推导了地层厚度的计算公式，对列氏公式进行了修正，分析了新公式的取值范围和角度误差影响，明确了“0值”和“负值”产生原因，理清了“负值”和“负厚度”概念的差异，并以实例验证了地层厚度计算公式。

1 地层真厚度计算公式

1.1 计算公式推导

列昂托夫斯基［20］提出的地层厚度计算公式一直为我国广大地质工作者所接受和使用［25-32］，要明确“0值”和“负值”现象，确定“负值”和“负厚值”概念，首先需理清地层厚度计算公式的准确性、正确性和适用性。野外实测剖面时地层倾向与测绳经过的地面坡向存在三种情况（图1）：①地层倾向与测绳经过的地面坡向相向；②地层倾向与测绳经过的地面坡向相同，坡度角大于地层倾角；③地层倾向与测绳经过的地面坡向相同，坡度角小于地层倾角。

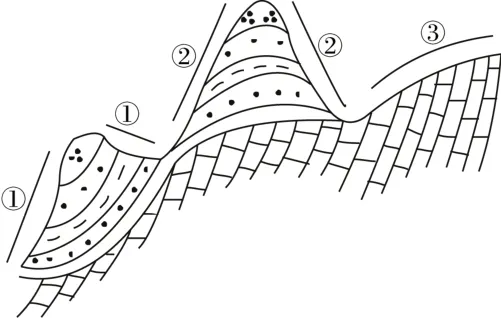
图1 实测地层剖面测线坡度角与地层产状关系示意图Fig.1 Schematic diagram of the relationship between the slope angle and the stratum dip angle in the field measured profile

图2 中两不同灰度的面Sabcd和Sefgh是两个平行的层面，Sbcgf是水平面，SADE是垂直于Sabcd和Sefgh的平面。从Sabcd和SADE的交线上的点E向面Sefgh做垂线EF，EF位于面SADE上，F为垂足，因此EF为两个平行层面的垂线段长度，即为地层真厚度。Sbcgf与Sabcd、Sbcgf与Sefgh的夹角即为真倾角，图中用α表示。线段AB为导线经过地面斜坡的导线斜距，过A点做面Sefgh的垂线，垂足为C，∠ABC为坡角，用β表示。∠γ为地层倾向与测绳经过的地面坡向的锐夹角。

由图2a知，

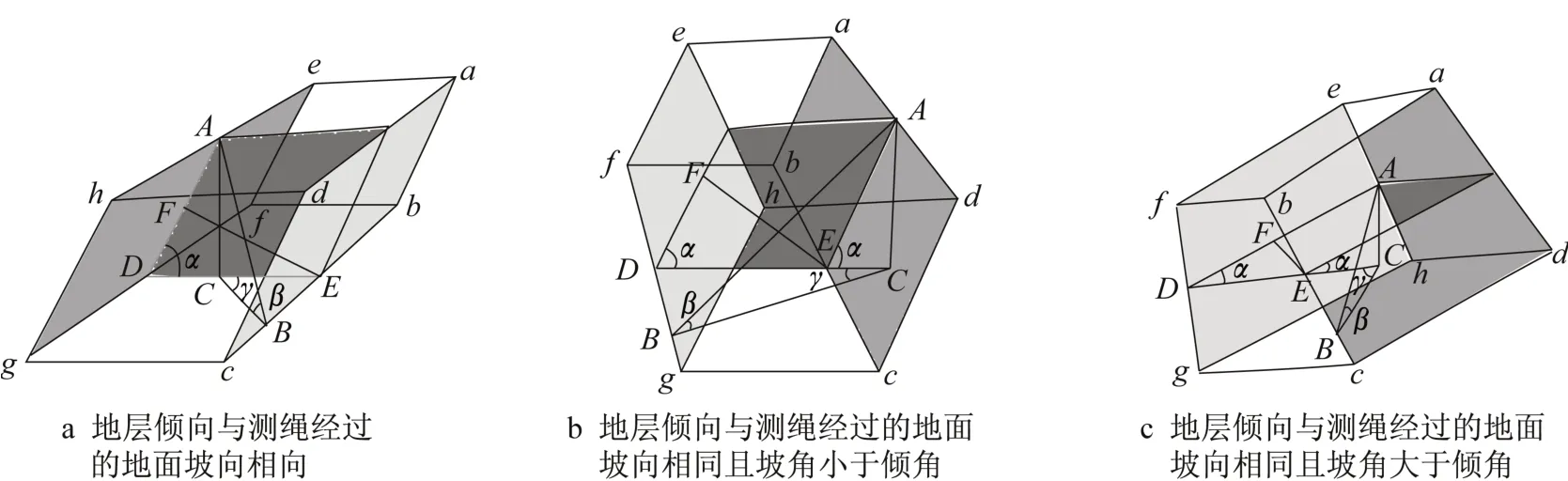
图2 地层真厚度计算模型Fig.2 The calculation model of the stratum true thickness

由公式（1）可得，

由图2b知，

由公式（3）可得，

由图2c知，

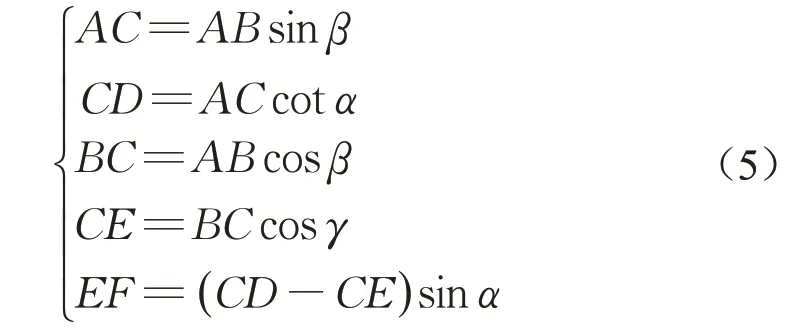
由公式（5）可得，

由式（2）、（4）、（6）可得地层总厚度计算公式为

设φ表示导线与地层走向之间的锐夹角，则φ与γ互余，由公式（7）得

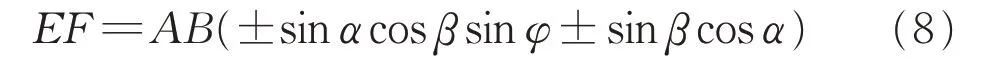
可知当地层倾向与测绳经过的地面坡向相向时，式（7）、（8）取“+”、“+”；当地层倾向与测绳经过的地面坡向相同且坡角小于倾角时，式（7）和式（8）取“+”、“-”；当地层倾向与测绳经过的地面坡向相同且坡角大于倾角时，式（7）和式（8）取“-”、“+”。

1.2 地层真厚度计算公式对特殊地层的适用性

为检测公式对特殊地层的适用性，进行了水平地层和垂直地层的验证。如图3 所示，两灰色面是平行的层面，AB是导线斜距，两个层面的垂线段是地层厚度，β是坡角。由图3a知水平地层厚度AC=ABsinβ；水平地层的真倾角α=0，代入公式（7）得：AC=ABsinβ，两者结果一致。由图3b知垂直地层厚度CD=ABcosβsinφ；垂直地层真倾角α=90°，代入公式（7）得：CD=ABcosβsinφ，两者结果一致。因此水平或垂直地层计算公式均为地层厚度计算公式（7）的特例。

图3 特殊地层厚度计算模型Fig.3 The calculation model of the stratum thickness in particular situation

2 地层厚度数值特征和误差分析

2.1 地层厚度数值取值特征

由公式（8）可知，因为测绳斜距恒为正，因此地层厚度值取决于地层倾角、坡角、导线与地层走向锐夹角的三角函数计算项的结果，即取决于公式（9）。

图2a 为地层倾向与测绳经过的地面坡向相向的情况，公式（9）取“+”、“+”，α为0～90°，β为0～90°，φ为60～90°，F值如图4所示。由图4a可知，地层厚度F值关于α=β和α+β=90°直线是近乎对称的，说明地层倾角和地层坡角对F值计算具有相同的影响；当φ值变小时，关于α=β的对称性变差，说明测绳与地层走向间的锐夹角影响了对称性；当α+β=90°时F值取得最大值，说明地层倾向与坡向垂直时F取得最大值；当α=β=0°或α=β=90°时F值取得最小值0，说明实测剖面是水平层面或垂直层面且测绳均为平移导线时，F取得最小值0。由图4b可知，F值随着φ值增大而增大，对F值影响范围为0～0.10，且F值越大变化范围越大。

图2b 为地层倾向与测绳经过的地面坡向相同且坡角小于倾角的情况，式（9）取“+”、“-”，α为0～90°，β＜α，φ值为60°～90°，F值如图5所示。由图5a可知，地层厚度F取值关于α+β=90°是对称的，随着地层倾角α的增大而增大，随着β的增大而减小；α=β时，F取得最小值，说明地层倾向与坡向近平行时F取得最小值；在α=90°、β=0°时取得最大值，说明地层倾向与坡向应近垂直时F取得最大值；φ值越小越影响F极大值。由图5b 可知，随着φ值增大F值增大，φ对F值影响范围为0.10～0.15。

图2c为地层倾向与测绳经过的地面坡向相同且坡角大于倾角的情况，式（9）取“-”、“+”，α为0°～90°，β＞α，φ值为60°～90°，，F值如图6所示。由图6a可知，地层厚度F取值关于α+β=90°是近乎对称的，随着α的增大而减小，随着β增大而增大；α=β时F取得最小值，说明地层倾向与坡向近平行时F取得最小值；α=0°、β=90°时取得最大值，说明地层倾向与坡向近垂直的取得最大值。由图6b可知，随着φ值增大，F值减小，φ对F值影响范围为0～0.05。

图4 地层倾向与测绳经过的地面坡向相向时地层厚度取值Fig.4 F-data variation map when the stratum dip direction is opposite to the slope direction of ground where the measure line passes

2.2 地层厚度误差分析

为了进一步分析地层厚度F值误差对地层真厚度计算的影响，掌握其误差变化特征，需对公式（9）计算F误差值。在α为0～90°，β为0～90°，φ为60～90°范围内，分别计算了三种情况下α、β、φ角分别误差1°时F的误差值。

当地层倾向与测绳经过的地面坡向相向时，误差分析结果如图 7 所示。图 7a 为α误差 1°时F的误差图，F 的误差值范围为-0.02～0.02，φ影响F误差极大值，φ值越小，F误差极大值越小；随着α增大，F误差由大变小，F误差绝对值先小后变大；随着β增大，F误差由大变小，F误差绝对值先变小后变大。图7b为β误差1°时F的误差图，F的误差值范围为-0.02～0.02，φ值影响F误差极小值，φ越小，F误差极小值越大、但绝对值越小；随着α的增大，F误差由大变小，其绝对值先变小后变大；随着β增大，F误差由大变小，误差绝对值先变小后变大。图7a和图7b表明在α、β极小或极大时，F误差绝对值最大，由图4a可知，此时F值较小，表明地层倾向与测绳经过的地面坡向近平行时α、β误差对地层厚度计算产生最大影响。图 7c 为φ误差 1°时F的误差图，F的误差范围为0～0.01，只有在大α值、小β、φ时，F误差较大，表明地层倾向与测绳经过的地面坡向近垂直时φ误差影响最大，且φ越小误差影响越大。

图5 地层倾向与测绳经过的地面坡向相同且β＜α时地层厚度取值图Fig.5 F-data variation map when the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is smaller than the stratum angle (β＜α)

图6 地层倾向与测绳经过的地面坡向相同且α＜β时地层厚度取值图Fig.6 F-data variation map when the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is bigger than the stratum angle (α＜β)

图7 地层倾向与测绳经过的地面坡向相向时地层厚度F取值误差分析图Fig.7 Error analysis chart of F-data when the stratum dip direction is opposite to the slope direction of the ground where the measure line passes

当地层倾向与测绳经过的地面坡向相同且β＜α时，F误差结果如图8所示。图8a为α误差1°时F的误差图，F的误差范围为0～0.02，随着α增大、β减小，F误差减小；φ越小，对小α、小β情况影响越大。图8b为β角误差1°时F的误差图，F的误差范围为-0.02～0，随着α增大、β减小，F的误差增大，但绝对值减小；φ值越小，对大α、大β情况影响越大。图8a和图 8b 均表明在β=α附近，F误差绝对值最大，由图5a可知，此时F值较小，说明地层倾向与测绳经过的地面坡向近乎平行时α、β误差对地层真厚度的计算影响最大。图 8c 为φ误差 1°时F的误差图，F的误差范围为0～0.01，只有在大α，小β、φ时，F误差较大，说明地层倾向与测绳经过的地面坡向近垂直时φ误差影响最大，且φ越小，F误差影响越大。

当地层倾向与测绳经过的地面坡向相同且β＞α时，误差结果如图9所示。图9a为α误差1°时F的误差图，F的误差范围为-0.02～0，随着α增大、β减小，F误差减小但其绝对值增大；φ越小，对小α、小β情况影响越大。图9b为β误差1°时F的误差图，F误差范围为0～0.02，随着α增大、β减小，F误差增大；φ越小，对大α、大β情况影响越大。图 9a 和图 9b 表明，在β=α附近，F误差绝对值最大，由图6a可知此时F较小，说明地层倾向与测绳经过的地面坡向近平行时，α、β误差对地层真厚度的计算影响最大。图9c 为在φ误差 1°时F的误差图，F误差范围为-0.006～0，只有小φ且α与β取值相近时，F误差较大，说明地层倾向与测绳经过的地面坡向近平行时φ误差影响最大，φ值越小误差影响越大。

3 “0值”和“负值”讨论

当式（9）F为0 时，地层厚度为0，包括以下几种情况：①由图4a可知，在地层倾向与测绳经过的地面坡向相向情况下，α=β=0°或α=β=90°时，F为0，说明地层水平或垂直且在层面拉测线时，地层厚度为0。②由图5a可知，在地层倾向与测绳经过的地面坡向相同且α＞β情况下，φ≠90°，α=β=0°或α=β=90°时，F为0；当φ=90°，α=β时，F为0，均说明在地层倾向方向沿层面拉测绳时，地层厚度为0。③由图6a 可知，在地层倾向与测绳经过的地面坡向相同且α＜β情况下，φ≠90°，α=β=0°或α=β=90°时，F为0；当φ=90°，α=β时，F为0，均说明在地层倾向方向沿层面拉测绳时，地层厚度为0。

图8 地层倾向与测绳经过的地面坡向相同时且β＜α时地层厚度F取值误差分析图Fig.8 Error analysis chart of F-data when the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is smaller than the stratum angle (β＜α)

当式（9）F为负时，计算的地层厚度才为负。F为负时，可能包括以下几种情况：

（1）地层倾向与测绳经过的地面坡向相同且坡角小于倾角时，欲使F为负，坡角须位于最小β线上方（图10）。

在地层倾向与测绳经过的地面坡向相同且坡角小于倾角的情况下，S1 和S2 是平行层面，受三维空间角度关系影响（图11），易知，

由图11 可知，θ＜α，由γ与φ互余知，γ为0°～30°，因此可得，

令tanη=tan αcosγ，则β＜η

计算结果如图10所示，β取值位于最大值η线下方，最大η线均位于最小β线下，说明在α、β、φ定义域内受三维空间角度关系制约，F不为负。

（2）地层倾向与测绳经过的地面坡向相同且坡角大于倾角时，按列氏地层厚度公式计算，倾向与坡向相同，因此式（8）取“+”、“-”，可得

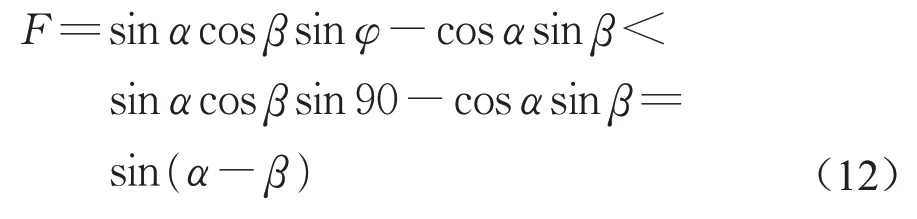
因此α＜β，式（12）必小于0。

若考虑坡角与倾角关系，α＜β时，式（8）取“-”、“+”，此时有

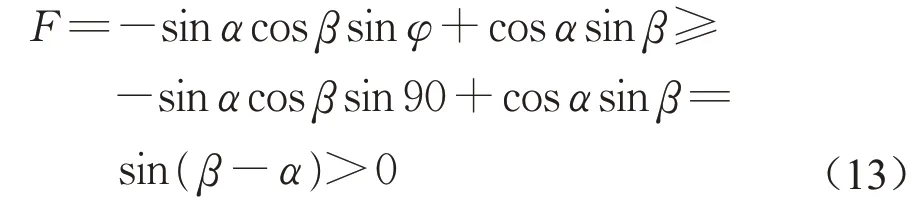
图9 地层倾向与测绳经过的地面坡向相同时且β＞α时地层厚度F取值误差分析图Fig.9 Error analysis chart of F-data when the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is bigger than the stratum angle (β＞α)

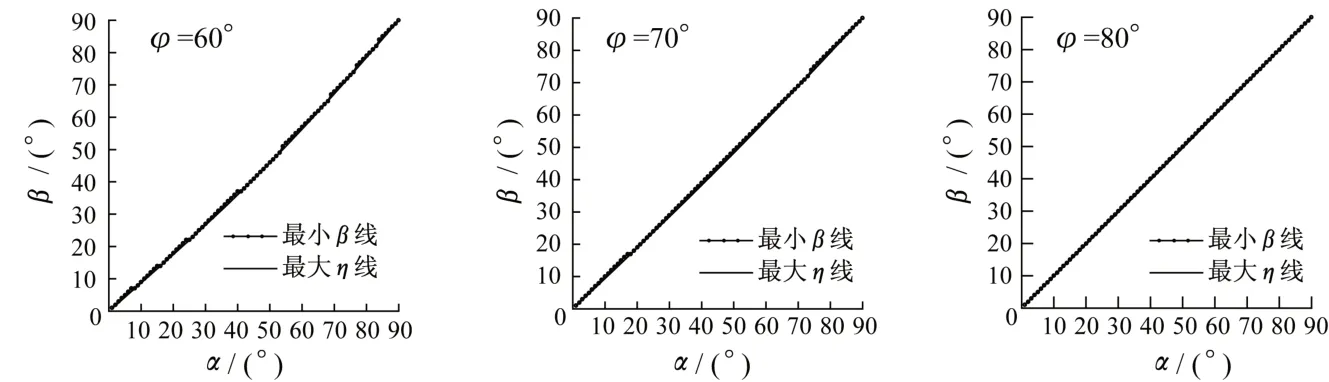
图10 地层倾向与测绳经过的地面坡向相同且α＞β的情况下F值为负值时的坡角分析图Fig.10 The analysis map of the slope angle when the F-data is negative under the situation that the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is smaller than the stratum angle (α＞β)

从文献［1］可以看出，列氏公式只强调地层倾向与测绳经过的地面坡向之间的关系，分为相同与相向两类，没有考虑倾角与坡角关系，当倾角小于坡角时，根据列氏公式必然为负（公式12）；而由图2c 可知，导线无论由上层面到下层面还是从下层面到上层面，地层厚度真实客观存在，计算结果与实际地层空间关系不符。而式（13）计算结果与实际地层空间关系相符，说明改进公式的正确性，同时也说明列氏公式不全面，缺失了野外实际情况，且列氏公式计算的负值不具有地质意义，后续实例分析也可证明，前人往往采用取绝对值进行处理［25］。

地层真厚度公式在沉积盆地分析、构造岩相分析与古地理恢复等研究中具有重要的价值。众所周知，沉积盆地分析、构造岩相分析与古地理恢复的基本研究手段是岩石地层剖面的测制，根据剖面所揭示的地层发育、岩性、岩相、厚度、接触关系及它们的时、空变化特点，恢复各地质时期的古地理（包括海陆分布、海侵方向、海水深度等）、古气候、古地貌（隆起-剥蚀区与坳陷-沉积区）、地壳沉降幅度（即沉积物厚度的相对大小）与速度（快速或逐渐堆积）、古构造状况以及演化历史等。显而易见，地层真实厚度的客观准确反映是正确分析古地理、古地貌、古构造运动的重要前提和必由途径，地层厚度计算公式的补充完善在科学研究与生产实践中均具有潜在的应用价值。

4 实例分析

文中选用了包含图1中所有情况的安徽省明光市杏山新近纪中新世下草湾组（N1x）—上新世桂五组（N2g）实测剖面，验证本文所完善的地层厚度计算公式。为了突出反映问题，选取了部分导线数据（表1），对比了列氏公式、矢量厚度公式［31］和本文的厚度计算公式的计算结果（表1）。

从表1中可以看出，列式公式计算的负值是表1中3―4 导的4、5、6 分层，地层均是在地层倾向与测绳经过的地面坡向相同且倾角小于坡角的情况，说明列氏公式本身缺失一种实测情况，使实际地层厚度出现负值，列式公式计算的厚度负值不能看作“负厚度”。矢量厚度计算公式的特点是不需要进行公式正负符号选择，矢量厚度公式计算的负厚度是表示由上层面到下层面测量、正厚度表示由下层面到上层面测量，计算总厚度时可以直接把负厚度舍去，只累加正值［31］。

图11 地层倾向与测绳经过的地面坡向相同且α＞β 的情况下三维空间角度关系Fig.11 Three dimensional spatial angle diagram under the situation that the stratum dip direction is same as the slope direction of the ground where the measure line passes and the slope angle is smaller than the stratum angle(α＞β)

但从表1中可以看出，6―7导的12、13分层，8―9 导的14、15 分层都是由上地层到下地层的测量方法，而计算结果为正值；9―10导的17分层是由下地层到上地层的测量方法，而计算结果为负值，可以看出矢量厚度公式由下―上地层的测量方法并非全为正，由上―下地层的测量方法也并不全为负，上述不符合矢量厚度计算公式表述的地层都是地层倾向与测绳经过的地面坡向相同且坡角小于地层倾角的情况，这是由矢量厚度公式直接去除负号的处理方式造成的。矢量厚度公式结果由上―下不全为负和由下―上不全为正（表1），因此总厚度计算时不能简单正值相加，对于构造复杂地区的地层总厚度，更应该计算出所有层的厚度，结合构造分析把有效地层进行相加。本文改进的厚度计算公式对所有野外测量情况计算结果全为正（表1），结合构造特征，更能有效计算地层总厚度。

表1 安徽省明光市杏山新近纪中新世下草湾组（N1x）—上新世桂五组（N2g）实测地质丈量表及计算结果对比Tab.1 Comparison table of geological survey and calculation results of Xiacaowan Formation of Neogene Miocene (N1x) to Guiwu Formation of Neogene Pliocene (N2g) at Xingshan of Mingguang city, Anhui province

5 结论

通过对实际测量情况下的地层厚度公式的推导、地层厚度取值范围和误差分析、“0值”“负值”的讨论及实例验证，主要得到了以下几个认识：

（1）列氏地层厚度计算公式不全面，不包括所有的野外实测情况，对其进行了修正，新的地层厚度计算公式为EF=AB(±sinαcosβsinφ± sinβcosα)，其中α是真倾角，β是坡角，φ是测线与地层走向之间的锐夹角，当地层倾向与测绳经过的地面坡向相向时，取“+”、“+”；当地层倾向与测绳经过的地面坡向相同且坡角小于倾角时，取“+”、“-”；当地层倾向与测绳经过的地面坡向相同且坡角大于倾角时，取“-”“+”。

（2）三种情况下F值随着α、β、φ具有各自不同的变化规律，但均在地层倾向与测绳经过的地面坡向近垂直时取得最大值；均在地层倾向与测绳经过的地面坡向近平行时取得最小值。

（3）三种情下F误差随着α、β、φ具有不同的变化规律，但α、β角度误差均在地层倾向与测绳经过的地面坡向近平行时对地层厚度计算影响最大，φ角度误差均在测绳与地层倾向偏离最大时对地层厚度计算影响最大。

（4）地层倾向与测绳经过的地面坡向无论是相同还是相向，只有在沿层面拉测绳时（测绳不穿层），地层厚度才为0；运用列氏公式计算的“负值”，是由公式缺失一种野外情况造成的，不具有地质意义；“负厚度”概念，只在矢量厚度计算公式中具有意义，表明由上界面到下界面穿过地层；本文实例表明矢量厚度计算公式也缺失了野外实测情况，使正厚度并不能完全表示由下―上穿过层面，负厚度并不能完全表示由上―下穿过层面，总厚度也不能用正值相加获取；修正的厚度计算公式，计算值全为正，符合客观实际情况，结合构造分析，能够计算地层总厚度。