高中物理教学中的数学思想渗透

张金德

【内容摘要】数学学科以其計算过程直观、解题思路清晰为特点，在多门学科中起着工具性辅助的作用。新课程改革对学生多学科综合应用能力提出了更高层次的要求。本文简要分析函数与方程思想、数形结合思想、转化与归化思想等数学思想在高中物理教学中的渗透方式，对教师如何引导学生将数学思想应用到物理问题的解决进行思考和提出建议。

【关键词】数学思想  高中物理  教学方法

引言

十七世纪数学学科的快速发展为自然学科的研究提供了强有力的理论支撑和工具支持。利用数学思想解决物理问题，这一要求的提出使学生对数学基础知识有一定的掌握。物理问题的分析能力和多学科综合思维能力是更高层次的要求，教师应在教学过程中慢慢渗透数学思想，培养学生多学科结合的思维方式。本文笔者依据自己在多年教学中总结出来的经验，探讨数学思想在高中物理教学中具体有效的渗透方法。

一、函数与方程思想

函数与方程思想在物理学科中的应用主要表现在两个方面：一是找到物理量之间的函数关系，列出函数关系式，利用函数的极值、参数的取值范围等解决物理问题。二是在物理问题的研究过程中针对某些物理量构造中间函数，将函数作为辅助工具，将复杂的物理问题转化成直观简易的函数关系式。在“研究平抛运动”“生活中的圆周运动”“匀变速直线运动”“弹簧振子的振动规律”等物理问题的研究中，或利用函数关系式求值，或通过研究函数性质获得物理规律都不可避免的利用到函数与方程思想。例如，在《匀变速直线运动》这一节中，若某质点的位移随时间的变化关系式求质点的初速度和加速度。教师可以引导学生将物理量一一映射到数学变量，通过对位移时间关系式的求导得出质点的初速度和加速度。同时，深刻理解数学中导数的含义为学生理解速度、加速度的概念提供一种新的思路。

二、数形结合思想

数形结合思想是解决高中物理问题的另一种常见思想。数形结合思想利用图形直观反映物理量之间定性的联系，从图中总结出物理量之间的关系，利用数学函数图像的增减性、极值等性质归纳出物理过程中隐含的规律。

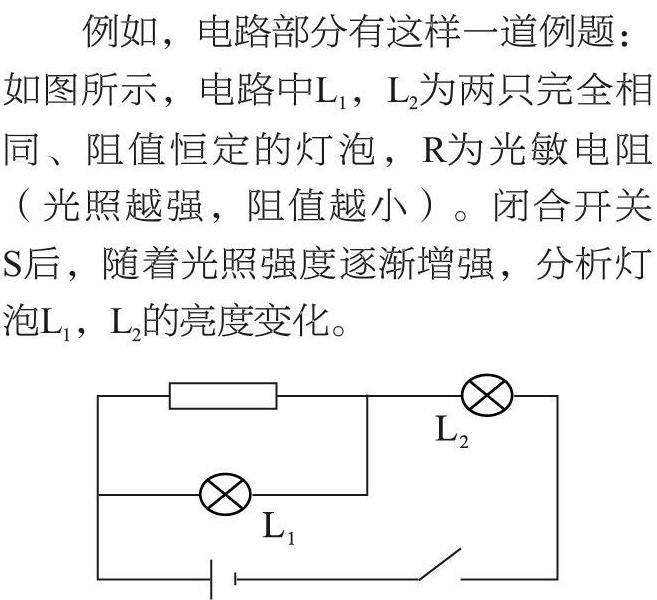
例如，电路部分有这样一道例题：如图所示，电路中L1，L2为两只完全相同、阻值恒定的灯泡，R为光敏电阻（光照越强，阻值越小）。闭合开关S后，随着光照强度逐渐增强，分析灯泡L1，L2的亮度变化。

在分析灯泡L1的亮度变化时，将灯泡L2等效为电源内阻。教师引导学生得出灯泡L1的功率P=-I2（R+r）+EI。P和I是二次函数的关系，做出P-I图像。根据二次函数的性质，结合对初始电流大小的分析就可以判断出随着光敏电阻阻值的减小，灯泡L2的功率会减小，即灯泡L2的亮度减小。通过本题可以总结出数形结合思想解决物理问题的具体步骤，首先应利用物理量之间的关系列出数学函数表达式。然后运用数学知识对图形进行分析，最终由数学量映射到物理量，归纳出物理过程的规律。数学图形以其能够清晰直观的反映出变量之间的变化规律和内在联系的特点在各个学科中都具有重要的应用价值，教师应引导学生尝试将数形结合思想应用于物理问题的解决中，培养学生观察图形、分析图形的能力。掌握好数形结合思想对于物理问题的解决能达到事半功倍、化繁为简的效果。

三、转化与归化思想

转化与归化思想是将一个问题由陌生化为熟悉、由复杂化为简单的过程。转化与归化思想不仅是一种解题策略，更是一种有益的思维方式。不仅在研究和解决物理问题时有重要价值，更对学生培养高效的思维方式和处事习惯有重要意义。例如，在天体运动中有A、B两颗卫星绕地心O做圆周运动，旋转方向相同，A卫星的周期为T1，B卫星的周期为T2，在某一时刻两卫星相距最近，求再隔多长时间，两颗卫星再次相隔最近。天体运动的问题因其复杂抽象的特点，学生常有“无从下口”之感。在这道题目中如果学生能够将复杂陌生的天体运动问题利用转化与归化思想转化成熟悉简单的相遇追及问题，再利用数学函数进行求解，从而达到化繁为简的高效求解。

结束语

数学思想在高中物理教学中的应用不止上文三种。无论采用哪种数学思想，重要的是教师需要引导学生学会找到物理学科和数学学科串联的入口，同时培养学生跨学科思维的能力，将已掌握的知识融会贯通、形成知识体系方能取用自如，适应高考千变万化的命题方式。

【参考文献】

[1] 王春燕. 在高中物理教学中如何应用数学思想与方法[J]. 学周刊，2017（5）：117-118.

[2] 丁国园. 高中物理教学中整合数学思想的实践探索[J]. 中华少年，2018（17）：137-137.

（作者单位：福建省浦城县第二中学）