集材机用三角履带轮关键参数的优化设计*

2020-07-28刘铁男王立海张广晖孟庆凯

林业科学 2020年6期

刘铁男王立海张广晖孟庆凯

(1. 东北林业大学工程技术学院哈尔滨 150040； 2. 黑龙江省森林工程与环境研究所哈尔滨150081)

我国自1998年开始施行天然林保护工程以来，森林采伐量逐年减少，功能单一的大型集材设备利用率逐渐下降，取而代之的是畜力集材作业；但随着林区劳动力成本不断提升，加之畜力集材作业方式存在成本高、效率低等问题，急需探索一种新型、高效、环保的多功能集材机械(王立海等， 2010)。根据林区生产实际，杨德岭(2013)研发出一种环保型多功能轮式集材机，该集材机集木材绞集、装卸、清障和修简易路等多功能于一体，具有外形尺寸小、转弯灵活、爬坡能力强等特点，不用修建集材道，可在林间穿行，对地表土壤破坏小，有很好的生态效益；同时，可以提高生产效率，降低生产成本，有较好的经济效益；此外，在非集材作业期还可用于采伐迹地的清理、整地、营林等多项作业，真正实现了一机多用。但该集材机在复杂的林地环境中功能会受到一定影响，其主要原因在于行走机构有待提高和优化。

三角履带轮是20世纪90年代发明的技术，其融合了履带和轮胎行走机构的优点，具有更高的通过性能，在国外现已广泛用于农用车辆、工程机械和军事装甲车上(Brownetal.， 1992； Ansorgeetal.， 2007； Servadio， 2010； Bessette， 2011； Kheirallaetal.， 2012； Hansen， 2013； Reshadetal.， 2014)。在国内，该项技术近年来逐渐受到重视，也得到了一定的研究和应用(钱珍宝等， 2012；傅德莲等， 2007；陈宁等， 2014；王胜军等， 2012；穆希辉等， 2014a; 2014b; 2014c；侯亮等， 2012)，但与国外相比还有较大差距，尚未形成一套科学的方法。鉴于此，本研究基于轮式集材机的基本参数和林内工况，提出集材机用三角履带轮结构技术方案，选取三角履带轮关键参数，并采用参数优化方法得到最优关键参数，以改善轮式集材机的通过性，提高集材机的牵引力和爬坡能力，为集材机用三角履带轮后续研究提供理论数据，为其他三角履带轮研发提供参考。

1 集材机用三角履带轮结构技术方案的确定

1.1 三角履带轮的结构组成及其作用

三角履带轮与传统履带相比，其构成基本相同，主要由框架、承重轮、导向轮、驱动轮、减震张紧装置和履带等部件组成(Nagorckaetal.， 2005；刘焕民等， 2004；杨立浩等， 2011；李立顺等， 2007；侯忠明等， 2009)。三角履带轮行走机构如图1所示。

图1 三角履带轮行走机构Fig.1 Structure diagram of walking device of triangular crawler wheel

框架结构大多为三角形，用于安装驱动轮、导向轮和承重轮等组件。三角履带轮的总体设计方案决定三角框架的结构形式，可分为中间支撑式和悬臂支撑式2种。中间支撑式三角框架主要用于重载的履带轮中，具有承载能力强和易于布局等特点；悬臂支撑式三角框架的承载能力相对较小，但其结构简单，易于加工，主要用于轻型和中型的履带轮中。

承重轮的主要作用是传递压力，使履带接地比压尽可能平均分布，其既可直接安装在三角框架底部，也可成对装配在摆臂悬架上，摆臂悬架再与三角框架连接(承重轮组对地面有一定的适应能力，更有利于应对起伏多变的地形、保持履带与地面的接触、缓冲振动、保护履带轮组件并提高舒适性)。

导向轮位于三角框架底部的两端或前端，主要用于引导履带。此外，导向轮与张紧装置一起可为履带提供张紧力，满足履带张紧需要。当导向轮的最低位置与承重轮相同时，导向轮也参与承重。如果工况复杂，障碍物较高，则需要导向轮的最低位置高于承重轮，以形成较大的接近角或离去角，为避障提供条件。

为了减少泥泞或碎石对驱动轮啮合的影响，通常将驱动轮安装在三角框架顶端。驱动轮直径一般小于原车轮胎直径，因此在相同运行条件下，装有三角履带轮的车辆行驶速度比原车行驶速度慢，但其牵引力会增大。

履带安装在轮系之外，直接与地面接触，将车体的质量传给地面，履带的选择直接关系到车辆的接地比压和附着性能。由于履带工作性质原因，其是三角履带轮中最容易破坏的部件之一，因此履带需具有强度大、耐磨性好的特性。

1.2 集材机用三角履带轮结构技术方案的确定

研发集材机用三角履带轮，重点是应对林内复杂工况，保证集材机的通过性，提高集材机越障能力并减少地面激励对集材机车体的冲击等。通过对三角履带轮结构组成及其作用的分析，本研究选择中间支撑式三角框架；为保证集材机具有较强的越障能力，需要导向轮的最低位置高于承重轮，以形成足够的接近角或离去角；在结构上采取左右对称方式，使接近角和离去角相同；采用带有摆臂悬架的承重轮系，以更好适应林内工况，减少地面激励。

2 三角履带轮关键参数取值范围的确定

三角履带轮结构总体技术方案确定后，更重要的是选取关键参数。关键参数可分为总体参数和各部件主参数2类。

2.1 总体参数取值范围的确定

三角履带轮总体参数指长(L1)、宽(Q1)、高(H)等三维尺寸(图2)，影响三角履带轮总体参数最主要的因素是原轮式集材机的基本参数。轮式集材机的基本参数见表1。

图2 三角履带轮三维尺寸Fig.2 Three-dimensional dimensions of wheeled skidders

表1 轮式集材机的基本参数Tab.1 Basic parameters of wheeled skidders

三角履带轮长度(L1)由原轮式集材机安装轮胎部位的空间决定。通过对实车的测量，可用空间的最大长度为1 600 mm，因此本集材机选用的三角履带轮长度L1≤1 600 mm。

三角履带轮宽度(Q)即履带宽度，该参数在确定履带主参数时进行详细计算，此处不再赘述。

三角履带轮高度(H1)多数要比替换下的轮胎半径大，导致换装三角履带轮车辆的车身高度有所增加，而车身高度增加则直接影响车辆行驶的纵向稳定性。一般情况下，研究车辆的纵向稳定性分为2种工况：一种为上坡行驶工况，另一种为下坡行驶工况。如图3所示。

图3 最大纵工况Fig.3 Maximum longitudinal slope loading diagram

四驱车辆上坡行驶时需要满足的纵向稳定性条件为：

(1)

式中：b为重心距前轴的距离；h为重心高度；φ为附着系数。

通过式(1)可以推导出下式：

b>φh。

(2)

四驱车辆下坡行驶时需要满足的纵向稳定性条件为：

(3)

式中：a为重心距后轴的距离；h为重心高度。

通过式(3)可以推导出下式：

a≥φh。

(4)

将式(2)、(4)相加可推导出h<(b+a)/2φ，其中b+a为集材机的轴距，长度为2 000 mm；通过文献(同济大学， 1980)可知，在硬土地面上φ取最大值，为0.9。将2个数值代入到h<(b+a)/2φ中，计算得到h<1 111 mm，即只有当三角履带轮式集材机的重心高度h<1 111 mm时，才能满足其纵向稳定性要求。由表1可知，原轮式集材机的重心高度为1 000 mm，故三角履带轮高度与替换下轮胎半径的差值应小于111 mm，而原始轮胎半径为463 mm，那么三角履带轮高度(H1)不能超过574 mm。为了提高集材机行驶的安全系数，取H1≤574 mm。

2.2 各部件主参数取值范围的确定

2.2.1 履带主参数取值范围的确定履带的主要参数有履带节距(t)、履带宽度(Q)和履带接地长度(L2)，能否合理确定这些参数，直接影响三角履带轮的牵引附着性能。履带参数取值在传统履带底盘设计中有比较成熟的经验公式可参考，本研究借助这些经验公式进行计算。

履带接地长度(L2)与履带宽度(Q)相关联，二者取值关系到车辆接地比压能否满足实际工况要求。根据传统履带车辆的经验，除沼泽工况外，作一般用途使用的三角履带轮车辆履带宽度(Q)与履带接地长度(L2)的比值Q/L2应在0.36～0.44之间。计算得到L2的取值范围为731 mm≤L2≤1 091 mm。

2.2.2 承重轮主参数取值范围的确定通常情况下，承重轮半径(d1)与履带节距(t)存在以下关系：

0.75t≤d1≤1.5t。

(5)

将t的取值范围126 mm≤t≤147 mm代入式(5)，可以求得94.5 mm≤d1≤220.5 mm。

2.2.3 导向轮主参数取值范围的确定在三角履带轮中，导向轮不仅起到引导履带的作用，还要安装张紧装置，满足履带张紧需要，因此，导向轮半径(d2)应大于承重轮半径，这样有利于减少对履带的冲击，提高集材作业的平稳性；但考虑到三角履带轮整体尺寸的限定并防止干涉问题出现，导向轮半径也不能过大。由图4可知，导向轮半径(d2)与越障高度(H2)、三角履带轮长度(L1)、履带接地长度(L2)和承重轮半径(d1)存在一定几何关系。

图4 导向轮极限的布局Fig.4 Layout of guide wheel limit

根据图4所示几何关系，可以得到如下关系式：

(6)

其中：OO1=H2-d1，OO2=0.5L1-0.5L2-d2，将其代入式(6)得到下式：

分析式(7)不难发现，当越障高度(H2)一定，三角履带轮长度(L1)取最大值1 600 mm，承重轮直径(d1)取最小值94.5 mm，履带接地长度(L2)取最小值731 mm，导向轮与承重轮相切时，导向轮半径达到极大值。基于此假设条件，由式(7)可推导出下式：

(8)

分析式(8)可知，只要得到越障高度(H2)便可求出d2max，而越障高度(H2)取值取决于障碍物高度。在伐区，伐根是集材机面对的主要障碍物，根据对典型工况内100组伐根高度数据的调查和分析，约83%的伐根在300 mm以下，故本研究选定300 mm为障碍物高度。对于越障高度(H2)而言，只有大于障碍物高度，才能保证集材机顺利通过障碍物，因此，将H2取值为320 mm，代入式(8)计算得到导向轮半径极大值d2max=218 mm。该值是在极限假设条件下得到的，在实际应用中不会出现这种情况，故将d2的取值范围定为d1≤d2≤200 mm。

2.2.4 驱动轮主参数取值范围的确定通常情况下，三角履带驱动轮节圆半径(d3)要比替换下的轮胎半径小。根据履带车辆行驶理论可知，牵引力大小与驱动轮节圆半径呈反比关系，驱动轮节圆半径越小，牵引力越大，随之每次载量也会增大；与此同时，车辆行驶速度降低，增加每趟用时。每次载量和每趟用时是影响工作效率的2个重要因素，本研究从集材机牵引力(F0)理论计算入手，比对分析改造前后的工作效率，以得到改造前后运行速度之间的数学关系。

从图5的受力分析可知，集材机牵引力(Ft)为集材机的摩擦力(Fm)和原条的摩擦力(Fw)之和：

图5 三角履带式集材机作业受力分析Fig.5 Force analysis chart of triangle crawler skidder

Ft=Fw+Fm=(Gm+KW)g(μmcosγ+sinγ)+

Wg(1-K)(μwcosγ+sinγ)。

(9)

式中：γ为坡度(°)；Gm为履带式集材机质量(kg)；W为木捆质量(kg)；μm为集材机在集材道上运行的阻力系数；μw为原条在集材道上被拖曳的阻力系数；K为每趟应集原条捆的质量在集材机上的分配系数；g为重力加速度(9.8 m·s-2)。

由集材机功率、牵引力和速度之间的关系式P=Ftv，可推导出：

Ft=P/v。

(10)

式中：v为集材机的行驶速度(km·h-1)。

将式(10)代入式(9)，可以得到下式：

(11)

由表1可知，轮式集材机功率为65 kW，整机工作质量为5 000 kg，最大爬坡度为30°。由表2可知，轮式集材机在冬季压实雪路上运行的阻力系数为0.04，履带式集材机在冬季压实雪路上运行的阻力系数为0.13，原条在集材道上被拖拽的阻力系数为0.4。可以分别计算出改造前后运行速度与搭载原条质量的关系：

表2 集材机运行阻力系数Tab.2 Running resistance coefficient for log skidders

W1=16 931/v1-4 563；

(12)

W2=18 824/v2-4 381。

(13)

式中：W1为履带式集材机搭载原条的质量(kg)；W2为轮式集材机搭载原条的质量(kg)；v1为履带式集材机的运行速度(km·h-1)；v2为轮式集材机的运行速度(km·h-1)。

集材机工作效率用单位时间内的集材质量表示，即w=W/T，其中：W为每次载量，T为完成一趟集材所需时间。T可表达为距离与速度比，即S/v，将此式代入w=W/T，得到下式：

w=Wv/S。

(14)

将式(12)、(13)分别代入式(14)，得：

w1=(16 931-4 563v1)/S；

(15)

w2=(18 824-4 381v2)/S。

(16)

分析可知，只有三角履带轮式集材机的工作效率w1大于或等于轮式集材机的工作效率w2，才有改造的价值。故设w1≥w2，计算得改造前后的运行速度关系式为：

v1≤0.96v2-0.41。

(17)

已知轮式集材机运行速度为v2=2 km·h-1，通过式(17)可求得三角履带轮集材机运行速度v1≤1.51 km·h-1。

根据线速度与角速度公式v=ω·d，可得下列公式：

v1=ω1d3；

(18)

v2=ω2d0。

(19)

式中：ω1为三角履带驱动轮旋转角速度；ω2为轮胎旋转角速度；d3为三角履带驱动轮节圆半径；d0为轮胎半径。

将式(18)、(19)相比，得：

(20)

换装三角履带轮只是替换轮胎，不会改变集材机驱动轴输出的角速度。将ω1=ω2代入式(20)，简化得到v1=v2d3/d0≤1.51 km·h-1，式中v2=2 km·h-1，d0=463 mm，通过计算得到驱动轮节圆半径d3≤350 mm。

3 三角履带轮关键参数的优化选取

通常，参数优化设计包括目标函数、设计变量和约束条件3个要素，其中目标函数选取尤为重要。因为三角履带轮关键参数取值范围直接关系到三角履带轮的驱动效率，故本研究对三角履带轮驱动效率展开分析，建立相关目标函数，选取设计变量。借助MATLAB优化工具箱的优化计算方法，对所选取的关键参数取值进行优化分析，从而得到三角履带轮关键参数的最佳取值。

3.1 优化目标函数的建立

根据车辆前进后退，三角履带轮驱动效率可分为正向驱动效率和反向驱动效率。本研究三角履带轮采用左右对称结构，集材机反向行驶的驱动效率与正向行驶相同，故只对正向驱动情况进行分析。

当驱动力矩作用在驱动轮上时，履带驱动段(图6中1～5段履带)受有张力T=M/r(M为驱动力矩，r为驱动半径)。同时在驱动段，每当一块履带被卷上驱动轮，在履带销轴或芯金1两侧的履带相对转过∠θ，在履带销轴或芯金2、3两侧的履带分别相对转过∠β，在履带销轴或芯金4、5两侧的履带分别相对转过∠α。因此消耗的摩擦功为：

图6 履带内部受力Fig.6 Internal force diagram of the track

AK=μTr0(θ+2β+2α)。

(21)

式中：T为履带之间的拉力；μ为驱动轮与销轴或芯金间的摩擦系数；r0为销轴或芯金中部圆柱轴半径。

设驱动轮每旋转1周，有ZK块履带被驱动轮卷上，则驱动轮每旋转1周所消耗的功为：

LK=μTr0(θ+2β+2α)ZK。

(22)

驱动轮上的摩擦力矩为：

(23)

履带驱动段的功率损失为：

NμK=MμKωK。

(24)

式中：ωK为角速度。

履带驱动效率为：

(25)

(26)

式(26)中μ、r0为定值，只要(θ+2β+2α)/t取最小值，ημK便可取得最大值。因此，将下式选为目标函数：

(27)

式(27)中3个相对转角∠α、∠β、∠θ可通过几何关系求得。

履带在承重轮转过的相对转角为α(即为接近角)，根据图7所示几何关系可得到如下关系式：

∠α=∠ABC+∠ABD-90°。

(28)

式(28)中：

(29)

根据图7所示几何关系可知，AD=H2-d1、BD=0.5(L1-L2)-d2，将其代入式(29)，得：

图7 三角履带轮总体几何布置Fig.7 General geometric arrangement of triangular crawler wheels

(30)

式(28)中：

(31)

(32)

将式(30)、(32)代入到式(28)，得：

(33)

履带在导向轮转过的相对转角为β，根据图7所示几何关系可得到如下关系式：

∠β=270°-∠ABC-∠ABD-∠FBG-∠EBF。

(34)

式(34)中：

(35)

根据图7所示几何关系可知，FG=H1-H2、BG=0.5L1-d，将其代入式(35)，得：

(36)

式(34)中：

(37)

(38)

将式(30)、(32)、(36)、(38)代入式(34)，得：

(39)

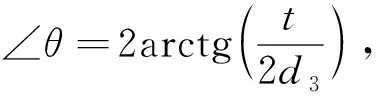
(40)

3.2 设计变量的选取

通过目标函数可知，涉及的变量为t、L1、L2、d1、d2、d3、H1，以这7个独立参数作为设计变量：

x=[x1,x2,x3,x4,x5,x6,x7]T=[t,L1,L2,d1,d2,d3,H1]T。

3.3 约束条件的确定

约束条件是对设计变量取值的限制，可分为以下5种形式：AX≤b(线性不等式约束)、AeqX=beq(线性等式约束)、C(X)≤0(非线性不等式约束)、Ceq(X)=0(非线性等式约束)、Lb≤X≤Ub(边界约束)。

本研究已经求出这7个关键参数的限制条件，下面按照5种形式将这7个关键参数的限制条件进行分类。

线性不等式约束有： 0.75x1-x4≤0、x4-

1.5x1≤0、0.75x1-x5≤0、x4-x5≤0。

边界约束条件有： 125≤x1≤147、1 300≤x2≤1 600、731≤x3≤1 091、94.5≤x4≤220.5、94.5≤x5≤220、300≤x6≤340、500≤x7≤575。

3.4 优化设计结果的分析

如式(40)所示，目标函数属于非线性规划最优化问题。采用约束非线性优化函数fmincon对所涉及的设计变量进行优化分析，从输出结果得到exitflag=1，表明优化一阶最优性条件满足容许范围，分析结果比较理想(表3)。根据优化结果绘制三角履带轮总体几何布置图(图8)，三角履带轮各部件之间不存在任何干涉，可根据该优化尺寸进行下一步具体设计工作。