基于人工神经网络模型的木材干燥应变模拟预测*

付宗营 蔡英春 高 鑫 周 凡 江京辉 周永东

(1. 中国林业科学研究院木材工业研究所 国家林业和草原局木材科学与技术重点实验室 北京100091； 2. 东北林业大学材料科学与工程学院 哈尔滨150040)

木材干燥是一个外部环境温度、相对湿度以及木材自身含水率、尺寸等的动态变化过程，无论是外部环境改变还是木材自身参数变化都将影响最终干燥质量，因此需根据木材自身含水率、各应变参数等变化对外部环境进行实时调整，即所谓的干燥基准。干燥过程中木材含水率、应力、应变的快速、精准检测一直是木材行业工作者研究的重点和难点，尤其对于干燥应力、应变，至今无快速、有效的检测方法(蒋佳荔等， 2005)。传统的切片法、叉齿法等可对某种干燥状态下瞬时的应力、应变进行一定描述，但费时费力，现有的应变片法、数字图像解析法等可对整个干燥过程中的应力、应变进行实时监控，但仅限于实验室使用，对于企业在实际生产过程中的应用依旧存在一定局限性，且其检测精度有待进一步提高(付宗营等， 2014)。

木材是一种弹塑性材料，在弹性范围内，应力消除后应变可完全恢复，应力、应变遵循胡克定律。弹性应变与干燥应力存在一一对应关系，即某含水率下的弹性应变可用来表征此时的干燥应力状态(李坚， 2014)； 而机械吸附蠕变关系到木材加工使用过程中的尺寸稳定性问题，其有利于释放部分干燥应力(Pang， 2000)。无论是弹性应变还是机械吸附蠕变，均受干燥温度、相对湿度等外部环境条件以及含水率、材性等木材自身性质影响，但对于具体的影响规律及机制目前尚无明确解释(Zhanetal.， 2011)。人工神经网络模型可有效处理非线性、复杂的模糊过程，其无需任何前提假设和理论关系分析，便可根据历史数据信息，通过强大的自组织整合能力建立有效的网络预测模型(Haganetal.， 1996)。人工神经网络模型在木材科学领域有着广泛应用，研究者们采用人工神经网络对木材导热系数(Avramidisetal.， 2005a)、介质损耗因子(Avramidisetal.， 2006)、木材密度(Iliadisetal.， 2013)以及非等温扩散条件下的木材水通量(Avramidisetal.， 2007)等进行预测分析，证实了人工神经网络强大的模拟预测能力。杨文斌等(2006)探讨了BP网络预测木材导热系数的可行性。Zhang等(2006； 2008)建立了时延神经网络基准模型，用于干燥过程中木材含水率以及温度、相对湿度的预测。Ceylan(2008)基于神经网络模型，以干燥温度、相对湿度、干燥时间为输入变量，预测了木材干燥过程中的含水率情况。Watanabe 等(2013； 2014)以初含水率、基本密度、年轮取向、年轮宽度、心材率、木材明度为输入变量，利用人工神经网络对气干材终含水率进行模拟预测，结果发现与主成分回归模型相比，人工神经网络预测模型更接近于实际气干材含水率； 同时参照偏最小二乘法模型，基于人工神经网络模型预测分析了木材表面干燥应力状况，得出近红外光谱试验值与预测值的相关系数为0.79，取得了较好预测效果。Bedelean等(2015)建立3层前馈型网络模型对北美红杉(Sequoiasempervirens)木和松(Pinus)木生材的高频加热速率进行模拟预测，敏感度分析显示，含水率对高频加热速率影响较大，而对基本密度影响较小。

本研究整合分析采用图像解析法测算得到的弹性应变和机械吸附蠕变相关数据，基于人工神经网络模型，以干燥温度、含水率、相对湿度、距髓心距离为输入变量对弹性应变进行模拟预测，以预处理温度、干燥温度、含水率、相对湿度、距髓心距离为输入变量对机械吸附蠕变进行模拟预测。通过网络训练和验证，得到合理的人工神经网络预测模型，并对模型进行测试，探讨分析所建立模型的预测能力，以期为人工神经网络在干燥应力、应变方面的应用提供可行性依据。

1 材料与方法

1.1 弹性应变和机械吸附蠕变检测

弹性应变和机械吸附蠕变检测采用图像解析法(付宗营等， 2014)，试验数据源自Fu等(2015)。如图1所示，首先将原木锯切为30 mm厚树盘，然后采用GDS-100恒温恒湿箱(上海一恒科学仪器有限公司)进行干燥，干燥至树盘平均含水率为26%、18%、10%时，将树盘锯解为应变测试试件，尺寸为30 mm(弦向)×10 mm(径向)×30 mm(纵向)。利用称重法对树盘含水率进行测试。

图1 树盘应变切片锯解及测试示意Fig.1 Cutting and testing diagram for wood specimens

弹性应变网络预测模型(M1)采用图像解析法检测的2种干燥基准(图2)、3个含水率阶段(26%、18%、10%)以及9个径向位置(沿髓心至树皮方向)的弹性应变数据，进行2组重复性试验，数据总数为162。机械吸附蠕变网络预测模型(M2)采用图像解析检测的3种类型试材(素材、80 ℃饱和湿空气处理材和100 ℃饱和蒸汽处理材)、3个含水率阶段(26%、18%、10%)以及9个径向位置(沿髓心至树皮方向)的机械吸附蠕变数据，进行1组试验，数据总数为162。

图2 2种干燥基准(S)下干球温度(T)、含水率(MC)和相对湿度(RH)随时间变化曲线Fig.2 Plots of dry bulb temperature (T), moisture content (MC) and relative humidity (RH)with drying time under two drying schedules (S)

1.2 人工神经网络模型分析

弹性应变和机械吸附蠕变网络预测模型均采用3层前馈型网络结构，包括输入层、隐含层和输出层，各层神经元仅与相邻层神经元之间全连接，同一层神经元之间无连接，各层神经元之间无反馈连接(Haganetal.， 1996)。对于该类型网络来说，隐含层神经元数量直接关系到模型的预测能力，若数量过多，不仅会增加网络训练时间，而且有可能出现过拟合现象； 若数量过少，则会导致模型训练不充分，不能全面表达输入变量与输出变量之间的关系，从而影响模型预测能力。隐含层神经元数量确定的一般原则是： 在可表达输入变量与输出变量之间关系的基础上，尽可能选用较少数量的神经元，以使网络结构相对简单。本研究采用网络结构增长型方法，即开始阶段，选用较少数量的隐含层神经元，通过网络训练测试学习误差； 而后逐步增加隐含层神经元数量，直至达到预设的目标学习误差为止； 最后，通过模型验证进一步优化网络结构。网络训练误差与隐含层神经元数量的对应关系如表1所示，M1(弹性应变网络预测模型)中神经元数量超过7个时，出现过拟合现象； 而M2(机械吸附蠕变网络预测模型)中神经元数量为8个时，已接近网络目标误差。因此，M1隐含层神经元数量最终确定为6个，M2隐含层神经元数量最终确定为8个。

表1 网络训练误差与隐含层神经元数量的对应关系Tab.1 Relationship between network training error and number of neurons

神经网络训练采用误差反向传播(back propagation)算法，选用trainlm(Levenberg-Marquardt)作为训练函数，主要包括3个阶段： 1) 学习信号的正向传播； 2) 计算以及相关误差的反向传播； 3)各层间权重值的调整(Avramidisetal.， 2005b； Tiryakietal.， 2014a)。将所有数据随机分为训练集、验证集和测试集3个数据集，其中训练集98个测试数据，占总数据的60%，验证集和测试集均为32个测试数据，分别占总数据的20%(Myharaetal.， 2001； Estebanetal.， 2009)。为了使传递函数更加有效，网络训练前采用式(1)对输入变量和输出变量进行标准化处理：

(1)

式中：X′为X的标准化值；Xmax和Xmin分别为X的最大值和最小值。

网络功能主要取决于不同层神经元之间的连接函数。一般认为，包括曲线函数和线性函数的2层网络结构，只要隐含层神经元数量足够，就可以描述输入层与输出层之间的任何函数关系(Sarle， 1995)。如式(2)所示，双曲正切函数作为输入层与隐含层之间的传递函数，而隐含层与输出层之间的传递函数选用线性传输函数：

(2)

式中： tan sig (x) 代表神经元的输出值；x代表神经元的输入值。

神经网络性能采用均方差(mean squared error，MSE)进行评价，如式(3)所示：

(3)

式中：n为数据的组数；ti为测试值；pi为预测值。

测试值与预测值之间的均方差越小，网络性能越好。同时，相关系数(R)和决定系数(R2)也作为神经网络性能的评价指标。学习效率设为0.01。

模型建立和模拟过程在MATLAB软件中进行。预测弹性应变的神经网络模型选用4-6-1网络结构形式(图3a)，输入变量为干燥温度、含水率、相对湿度和距髓心距离； 预测机械吸附蠕变的神经网络模型选用5-8-1网络结构形式(图3b)，输入变量为预处理温度、干燥温度、含水率、相对湿度和距髓心距离。

图3 弹性应变(a)和机械吸附蠕变(b)预测模型网络拓扑结构Fig.3 Network topology of elastic strain (a) and mechano-sorptive creep (b) prediction model

2 结果与讨论

2.1 人工神经网络模型对弹性应变的预测

训练集、验证集和测试集的均方差(MSE)随迭代次数的变化如图4所示。平行于横轴的虚线代表目标误差线，目标均方差为1.0×10-6。当迭代次数为17次时，验证集达到最优预测性能，此时MSE为1.21×10-6； 当迭代次数超过17次时，验证集的MSE将随迭代次数增加而增大。测试集的MSE随迭代次数的变化与验证集具有相似趋势。此外，在网络训练过程中无过拟合现象发生[过拟合现象被认为是神经网络训练过程中的一个严重问题，主要表现为验证集中误差增大以及训练集中误差减小(Sarle， 1995)],因此，可认为本研究建立的神经网络模型合理可靠。

图4 训练集、验证集和测试集的均方差随迭代次数的变化Fig.4 Plots of mean squared error (MSE) for the training, validation and test set with iterations

训练集、验证集、测试集和总数据集中，试验值与预测值之间的线性回归方程及对应的相关系数(R)和决定系数(R2)见表2。训练集、验证集、测试集和总数据集的R分别为0.988、0.983、0.978 和 0.985，而测试集的R2为0.95，表明该神经网络模型能够解释95%以上的试验数据， 其他3个数据集的R2均高于0.95。Mansfield等(2007)基于神经网络预测弹性模量时，数据集的R2为0.693～0.750，而预测静曲模量时，R2仅为0.438～0.561，是由于数据集不足以及输入变量选择不当造成的； Tiryaki等(2014b)基于神经网络模型预测热处理木材压缩强度时，所有数据集的R2均高于0.99。

表2 试验值与预测值之间的线性回归关系Tab.2 The results of linear regression between experimental and predicted values

弹性应变试验值与人工神经网络模型预测值的回归拟合情况如图5所示，彩色线条代表试验值与预测值的线性拟合关系。由图可知，训练集、测试集和总数据集中彩色线条几乎均在黑线之上，表明预测值与试验值拟合情况较好，训练所得的神经网络模型可成功预测干燥过程中的弹性应变。

图5 弹性应变试验值与人工神经网络预测值的回归关系Fig.5 Cross-correlation graph between experimental and ANN predicted values for elastic strain

图6为测试集中弹性应变试验值与预测值的对比关系。2种干燥基准下，含水率26%时均表现为拉伸弹性应变，而含水率18%和10%时拉伸弹性应变被压缩弹性应变所代替，同时含水率10%的弹性应变小于含水率18%的相应值。对于基准1，弹性应变沿髓心至树皮方向无明显变化趋势，且变化范围较小，尤其当含水率10%时，变化范围为-0.001～0.001。对于基准2，含水率18%和10%的弹性应变均随距髓心距离增加而增大，是由于沿径向存在含水率梯度以及不同径向位置材性差异所致。预测值与试验值相比，2种干燥基准下由训练好的神经网络模型所得几乎所有预测值都与相对应的试验值十分接近，只有基准2中含水率10%时距髓心70 mm处预测值与试验值之间有微小偏差。弹性应变试验值与预测值较好的吻合程度与上述测试集较高的R2相一致，再次证明本研究提出的人工神经网络模型预测弹性应变具有可行性。

图6 2种干燥基准下弹性应变试验值与预测值的对比关系Fig.6 Comparison of experimental and predicted values of elastic strain under two schedules

2.2 人工神经网络模型对机械吸附蠕变的预测

如图7所示，训练集、验证集和测试集的均方差(MSE)均接近于目标误差线。MSE随迭代次数增加逐渐减小，验证集达到最优预测性能时的MSE为1.26×10-6，此时迭代次数为37次。

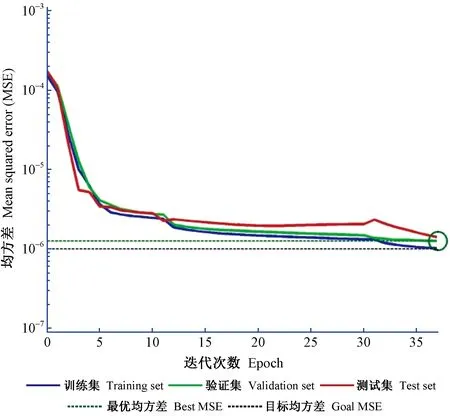
图7 训练集、验证集和测试集的均方差随迭代次数的变化Fig.7 Plot of mean squared error(MSE) in training, validation and test sets with iterations

训练集、验证集、测试集和总数据集中，试验值与预测值的线性拟合情况及其所对应的相关系数(R)和回归方程如图8所示。对所有数据集而言，试验值与预测值均表现出显著相关性，训练集、验证集、测试集和总数据集的R分别为0.981、0.977、0.969和0.978，R2均高于0.94，表明该神经网络模型能够解释94%以上的试验数据，表现出较好预测能力。

图8 机械吸附蠕变试验值与人工神经网络预测值的回归关系Fig.8 Cross-correlation graph between experimental and ANN predicted values for mechano-sorptive creep

含水率20%时，机械吸附蠕变试验值与预测值的对比关系如图9所示。可以看到，无论是处理材还是素材，试验值与预测值均十分接近，证实该神经网络模型预测机械吸附蠕变具有可行性。同时说明，若已知木材干燥过程的外部环境参数和木材本身相关参数，则可利用训练好的神经网络模型对机械吸附蠕变进行预测，从而省去复杂的试验检测过程，节约时间和成本。

图9 含水率20%时机械吸附蠕变试验值与预测值的对比关系Fig.9 Comparison of experimental and predicted values for mechano-sorptive creep model at moisture content of 20%

3 结论

弹性应变预测模型中，以干燥温度、含水率、相对湿度和距髓心距离为输入变量，训练集、验证集和测试集的相关系数(R)分别为0.988、0.983和0.978，所有数据集的决定系数(R2)均高于0.95，验证集达到最优时的均方差(MSE)为1.21×10-6，试验值与预测值吻合较好，证明用于预测弹性应变的网络模型具有较好的稳定性。机械吸附蠕变预测模型中，以预处理温度、干燥温度、含水率、相对湿度和距髓心距离为输入变量，对素材、80 ℃饱和湿空气处理材以及100 ℃常压饱和蒸汽处理材的机械吸附蠕变进行模拟预测。利用含水率28%和12%的数据集进行模型训练和验证，训练集和验证集的相关系数(R)分别为0.981和0.977，验证集达到最优时的均方差(MSE)为1.26×10-6； 利用含水率20%的数据集进行模型测试，试验值与预测值十分接近，测试集的相关系数(R)为0.969,所有数据集的决定系数(R2)均高于0.94，表现出较好的预测能力。本研究证实人工神经网络在干燥应力、应变模拟预测方面具有一定可行性。