紧支撑正交复小波滤波器的参数化

李林杉,胡琳,杨玉洁,方怡,师国伟

(1.北京联合大学基础与交叉科学研究所,北京100101;2.空军特色医学中心,北京100142)

1.引言

近年来,小波滤波器的理论和应用迅速的增加.正交性、对称性、紧支性是小波应用于工程中非常重要的特性.众所周知,除了Harr小波,不存在紧支撑并且对称正交的2 带实小波.为了克服这一缺陷,小波的概念被推广到高维小波[2−5]、多带小波[6]、多小波[7]、复小波[8−12]等.复数小波具有较好的方向性,平移不变性和精确的相空间等信息,使其在实际应用中比实小波更具有优势,因此复小波的研究受到人们的高度关注.这方面的文章不断涌现,构造的方法也各具特色.Lawton[7]构造了对称正交的复小波;Lina[9]从小波值域的拓展和构造平移不变的小波变换出发,提出了Daubechies复数小波的概念;ZHANG[10]和HAN[11]讨论了复小波的一些性质,做了进一步的研究;FENG[12]给出紧支撑复小波的参数化.本文受到文[12]的启发,给出了紧支撑正交复小波参数化的最简单的形式,比文[12]减少了参数的个数,更易于得到正交的复小波,从而为工程人员选择合适的复小波带来更大的方便,并给出了算例.

2.预备知识

由多分辨率分析知道,构造小波的方法通常开始于双尺度方程,尺度函数φ(x)和小波函数ψ(x)是小波理论的核心,但在工程实现时并不直接使用φ(x)和ψ(x),而是使用与他们对应的H(ξ)和G(ξ)的冲激响应{hk}和{gk}.构造小波实际上就是求解低通滤波器系数{hk}和高通滤波器系数{gk},而{hk}与{gk}的关系是确定的,即gk=(−1)n−1h1−k.[1]因此只需确定{hk},便可确定{gk},从而也就确定了尺度函数φ(x)和ψ(x).

定义2.5当滤波器{hk}、{gk},为满足正交小波条件的复数时,该滤波器即为复小波滤波器.

3.正交复小波滤波器的参数化结果

定理3.2H6(z) 满足H6(1)=1 ,|H6(z)|2+|H6(−z)|2=1,当且仅当:

证由条件|H6(z)|2+|H6(−z)|2=1,推出:

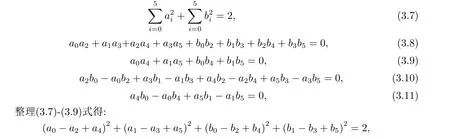
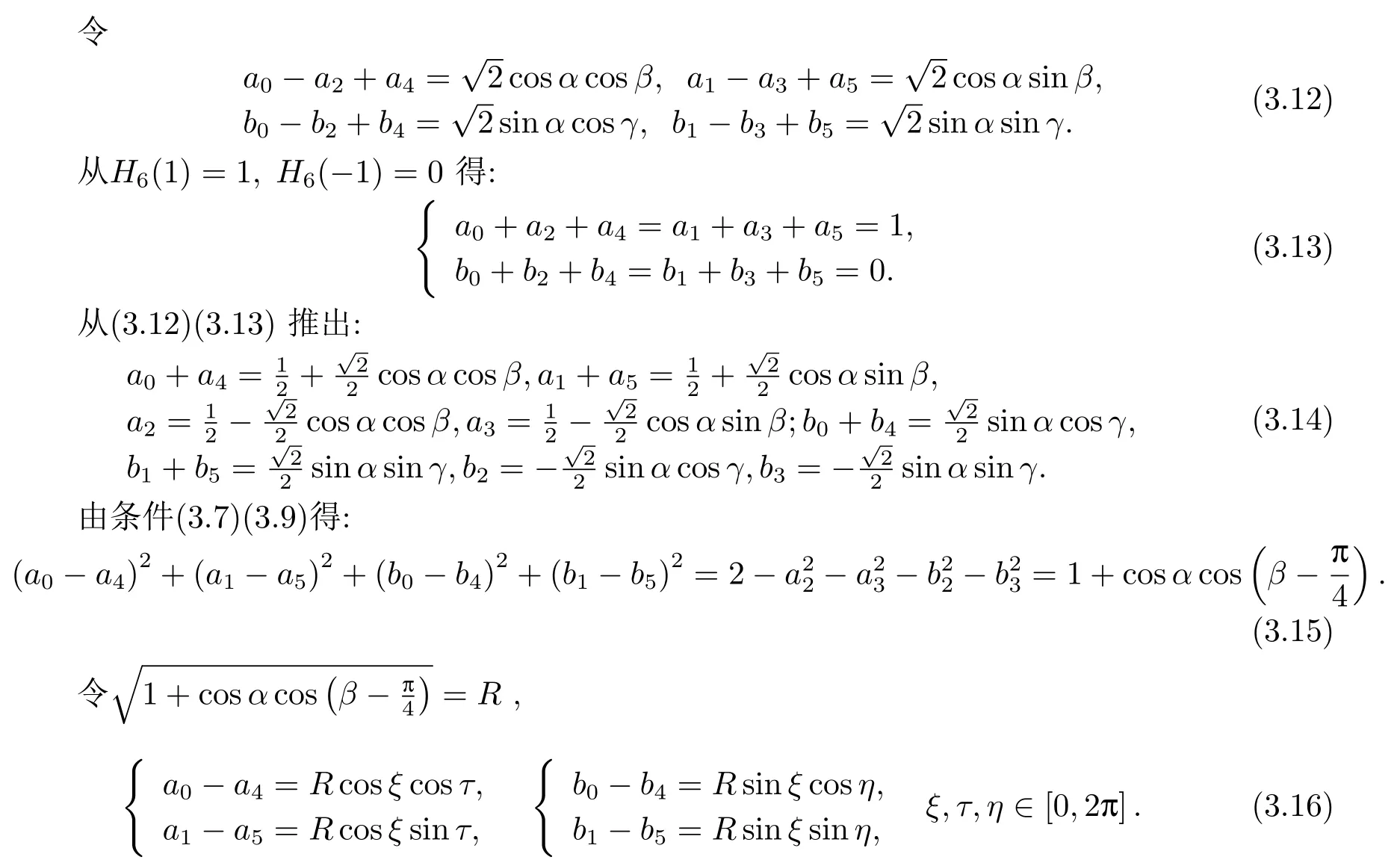
结合(3.15)(3.16)得:

4.结论

本文给出了长度为4、6的正交复小波滤波器的参数化,在目前所知的文献中参数的个数是最少的.在以后的工作中做更深入的研究,研究更高阶的复小波滤波器及具有消失矩、共轭对称等性质更好的复小波滤波器的参数化,以便于工程人员在解决实际问题中的有更好的应用.