次线性期望下独立同分布序列的一般强收敛性
2020-07-28陈滨霞吴群英
陈滨霞,吴群英
(桂林理工大学理学院,广西 桂林541004)
1.引言与预备知识
极限定理是概率论和统计学的重要研究课题,但随着极限理论在统计、金融风险度量等领域的应用更加广泛和深入,只能用于确定性模型的经典极限理论逐渐显现其局限性,因为在实际应用中,不确定性现象往往不能用确定性模型来建模解释.因此,PENG[1−3]在实践建模不确定性的激励下,引入了次线性期望的概念,将传统的概率和期望转化为容度和次线性期望.目前,次线性期望下的极限理论得到了越来越多的关注和研究,例如: ZHANG[4−6]深入研究了次线性期望空间,建立了指数不等式、Rosenthal不等式、强大数定律(SLLN)等一系列重要的不等式,WU和JIANG[7]也对次线性期望下的SLLN进行了系统性的研究.
在经典的概率空间背景下,Marcinkiewicz SLLN 结果为:对于独立同分布的随机变量序列,任意p ∈(0,2) ,存在着有限常数a,使当1≤p <2时,a=EX1;当0



2.主要结果


3.主要结果的证明



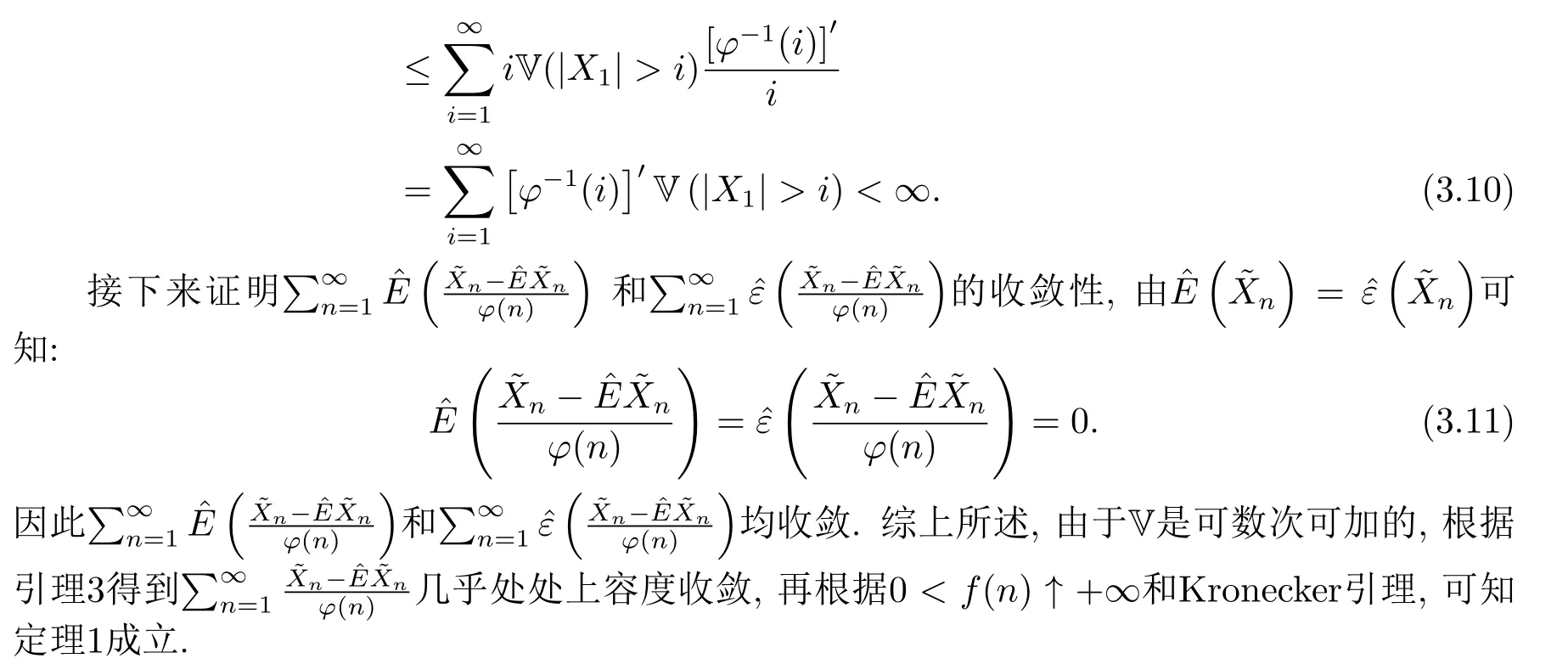
推论1的证明显然,f(x),φ(x)满足假设A的条件(i)和(ii),对于r ∈[1,+∞),

推论2的证明显然,f(x),φ(x)满足假设A的条件(i)和(ii),对于r ∈[2,+∞),


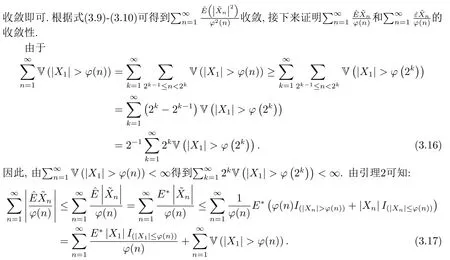
当定理2的(i)成立时,根据式(3.16)和式(3.17)得到:




推论3的证明如果0 由于在p=1情况下,用定理2的方法不能证明的收敛性,因此没有给出当p=1时Marcinkiewicz SLLN的证明.WU和JIANG[7]给出了在次线性期望空间中,当p=1时独立同分布随机变量序列的Marcinkiewicz SLLN的证明,值得注意的是,其文章所设定“为连续次可加”的条件只用在推导当p阶上积分发散时的情形,在推导当p阶上积分收敛的情形时仍用“为可数次可加”的条件.因此与本文定理2所采用的条件是一致的,故p=1时独立同分布随机变量序列的Marcinkiewicz SLLN也成立.综上所述,结合我们已经证明的p≠1时的Marcinkiewicz SLLN情况,最终得到: 成立,推论3证毕.

