二元紧耦合多入多出系统解耦匹配网络

李方华，李岳衡，张燕华，薛团结，周思源

(河海大学 计算机与信息学院，江苏 南京 211100)

多入多出(multiple-input multiple-output，MIMO)多天线传输技术在小尺寸移动终端应用时，狭小空间上所装配的多天线阵元由于尺寸的严格受限，将无可避免地产生严重的电磁耦合效应[1]，从而增大信号之间的相关性[2]，最终影响整个系统的信道容量或者说传输速率[3]。如何抑制紧凑型MIMO系统阵元间的耦合[4-12]效应，成为新一代移动通信系统所必须面对的技术难题之一。Zhao等[4]、Xia等[5]采用由带有耦合的谐振器组成的去耦网络来解耦2个天线之间的耦合效应，缺点是随着天线间耦合效应的增强，定向耦合器的实现愈加困难。Fei等[6]以最大化MIMO系统信道容量为目标，提出了一种最优单端口自阻抗匹配的概念来部分平衡天线阵元间的耦合效应；Mohammadkhani等[7]分析了上述单端口最优阻抗负载方案的缺点，即需要预先知道信道和耦合模型这一实际系统中较难获得的先验信息，提出了一种直接处理接收信号的改进自适应方案来动态解耦合。Masouros等[8]采用基带预编码方法对大规模MIMO系统的耦合效应加以改善，缺点是其模型的建立是基于传统的简单偶极子阻抗模式，实用天线场景受到限制。Li 等[9]研究了基于接收互阻抗的方法来补偿互耦效应，该方法会导致紧凑阵列的功率匹配降低，进而影响系统容量。Wallace等[13]基于天线S散射参数理论，提出了一种多端口共轭匹配网络，可以完全消除因阵元耦合效应所引发的信号相关性及入射波反射，从而令接收信号功率最大，系统容量得到极大改善。不过，该论文仅给出了多端口共轭匹配网络的S参数数学理论描述，并未有相对应的微波电路设计与实现方案；Puente-Garcí等[14]在此理论基础之上，给出了多端口共轭匹配网络的微带电路理论设计架构，但仍没有具体的电路设计过程或案例。本文根据微波电路基本原理，提出了一种适用于2×2紧耦合MIMO系统的多端口共轭匹配网络的具体电路设计，并给出其相应的计算机电磁仿真结果和电路实测数据，以验证设计的合理性。

1 解耦匹配网络的理论设计原理

1.1 解耦电路的设计原理

二阵元天线解耦匹配网络模型如图1所示。抑制耦合电路单元实现对天线阵元间耦合的解耦；T1和T2分别是天线阵元1和天线阵元2的阻抗匹配电路单元；P1和P2表示馈线端口，A、B、C分别表示不同电路节点的参考面。由微波网络技术[15-16]可知，对于双天线阵列系统，从参考面A得到的天线端口S参数矩阵为：

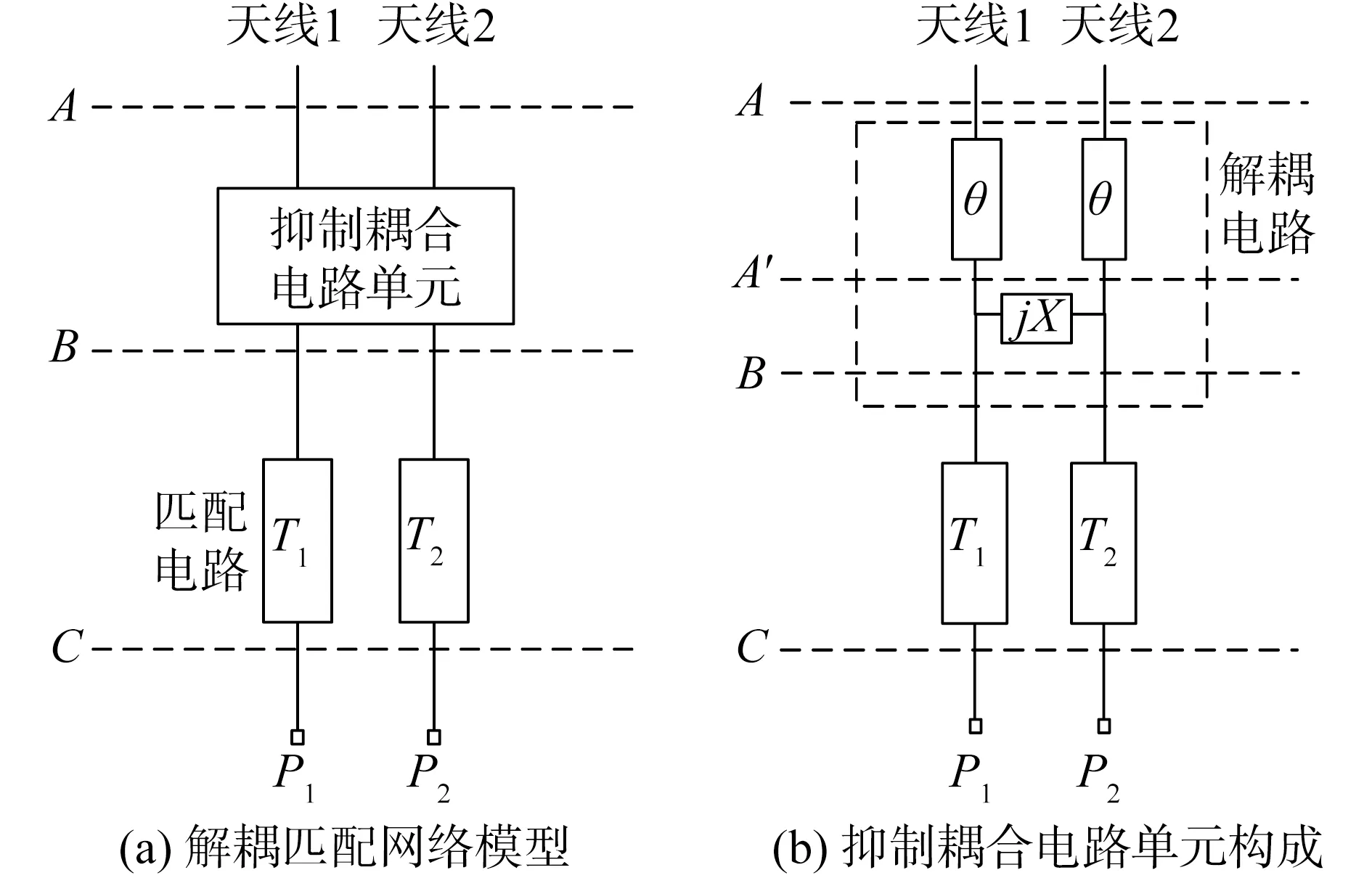
图1 二阵元天线解耦匹配网络设计原理Fig.1 Designing schematic of the two-element antenna decouping matching network

(1)

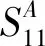
因为天线阵列单元与抑制耦合电路单元为并联关系，根据电路分析理论可知，并联电路最好选用导纳参数分析，所以将参考面A处的S参数矩阵，即式(1)通过微波网络理论转变成归一化导纳矩阵，如果天线阵列已经基本匹配，即天线端口自反射系数很小，则可推导出[16]：

(2)

式中：jX表示导纳；Y0=1/50 S

由计算和仿真发现，天线参考面A处的S参数均为复数。即若对参考面A处的S参数解耦，需要在抑制耦合电路单元中加入电阻。然而电阻是耗能元件，需要在抑制耦合电路与天线阵列之间加入特征阻抗微带线以对S参数进行移相，从而使抑制耦合电路呈现为纯电抗属性。

(3)

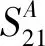
将式(3)的S参数矩阵再变换为Y导纳矩阵：

(4)

因为加入移相微带线后，在参考面A′处的互耦合系数实部为零，即：

(5)

从而求得移相微带线的理论电长度为：

(6)

式中k为整数，若无特殊要求，k=0。移相微带线太大或太小都会影响耦合电路的设计。将式(6)代入式(4)得到：

(7)

由图1(b)可知在参考面B处的Y参数矩阵为：

(8)

由S参数与Y参数的转换关系可知，互阻抗为零等价为互导纳为零，所以天线去耦合等价于：

(9)

其中，由式(9)确定的去耦元件既可以为电感也可以为电容等分立元件，若φ-2θ=2kπ-π/2时，去耦元件是电容，根据jX=jωC可计算出电容理论数值为：

(10)

式中f0是谐振频率。若φ-2θ=2kπ+π/2时，去耦元件是电感，由电感阻抗公式可得电感数值为：

(11)

由以上分析可知，确定式(6)的移相微带线[17]的长度就可以使电容或电感元件达到去耦效果。此时，从参考面B处向二元天线阵列方向看过去，天线的所有端口都已完成解耦。不过，该添加的解耦网络会对原各端口的特性阻抗产生破坏作用，所以随后还需要额外添加阻抗匹配网络以使各端口间阻抗匹配。

1.2 单枝节微带匹配电路设计原理

阻抗匹配就是在负载和源之间加入无源网络，实现源阻抗与负载阻抗的共轭匹配。对于微波电路，不管是无源电路还是有源电路，都要考虑阻抗匹配的问题。因为微波电路中传输的是导行电磁波，其阻抗不匹配将会引起严重的电压或电流反射。所以阻抗匹配就是微波电路(包括天线)设计时必须考虑的核心问题之一。

为了解决负载阻抗与传输线间的匹配，本文拟采用微波匹配网络电路设计中常用的单支节短截线匹配方法[15，18]。该方法在距离负载某一距离时使用单个开路的微带传输线与其他传输线进行并联。该匹配网络的拓扑结构为负载ZL与传输线串联后再与开路短截线并联。此方法的优势是微带线能够通过光绘工具实现，且易于加工。

图2为通过HFSS和ADS电磁软件混合仿真设计的原始天线、仅去耦天线及去耦匹配天线的微带布局模型图。根据上述短截线匹配电路理论，本文采用ADS电磁仿真软件，设计了一个谐振频率为2.35 GHz，源阻抗为50 Ω，负载阻抗为(30+j32)Ω的单枝节匹配网络，电路原理图如图3所示，而其所对应的匹配后S参数如图4所示的。从图4中可以看出，在中心频率2.35 GHz处，匹配网络的反射系数很小，S11为-31.963 dB，远小于-10 dB，该设计很好地实现了单枝节匹配网络的功能需求。从ADS仿真结果可以直接读出匹配微带线宽度为0.792 mm，短截线线长6.224 mm，另一微带线的线长为23.648 mm。至此，匹配电路各个参数的理论值已经计算完成；接着就是以此为初值，在HFSS软件中进一步作优化，最终得到匹配微带线宽度为1.5 mm时达到最优。

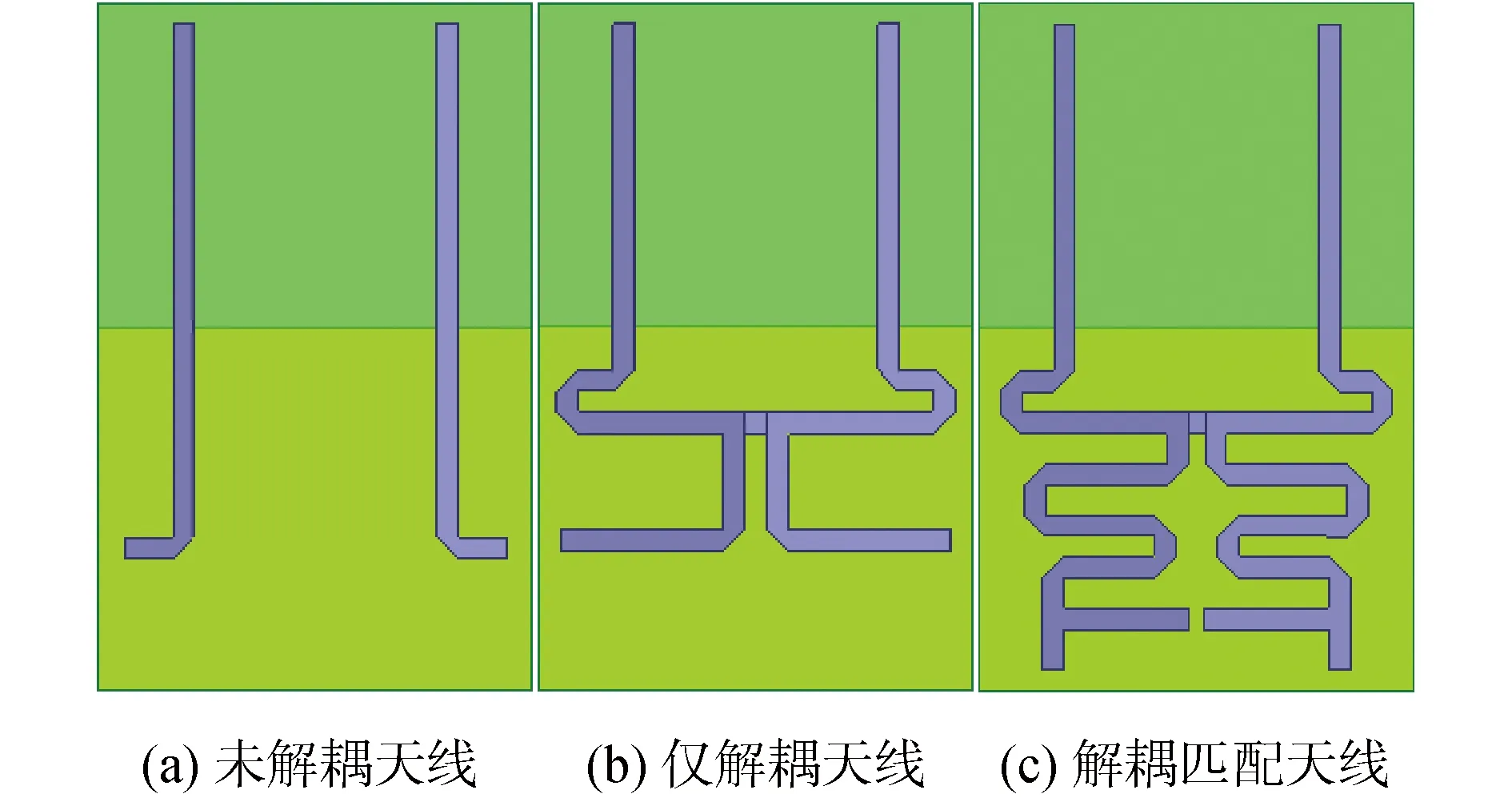
图2 3款天线阵列的HFSS设计模型Fig.2 HFSS design layouts of three kinds of antenna arrays

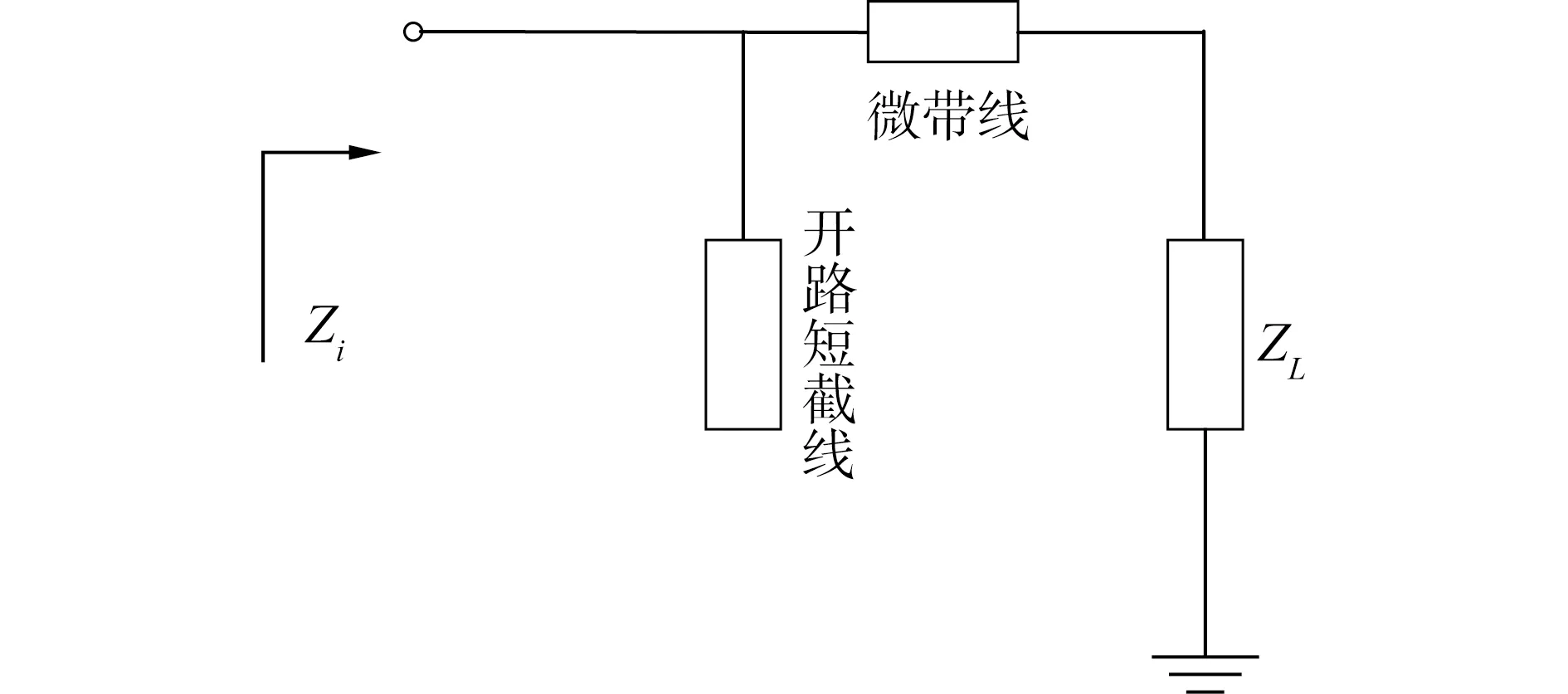
图3 单枝节开路短截线匹配电路结构Fig.3 Block diagram of the single branch open circuit stub matching network

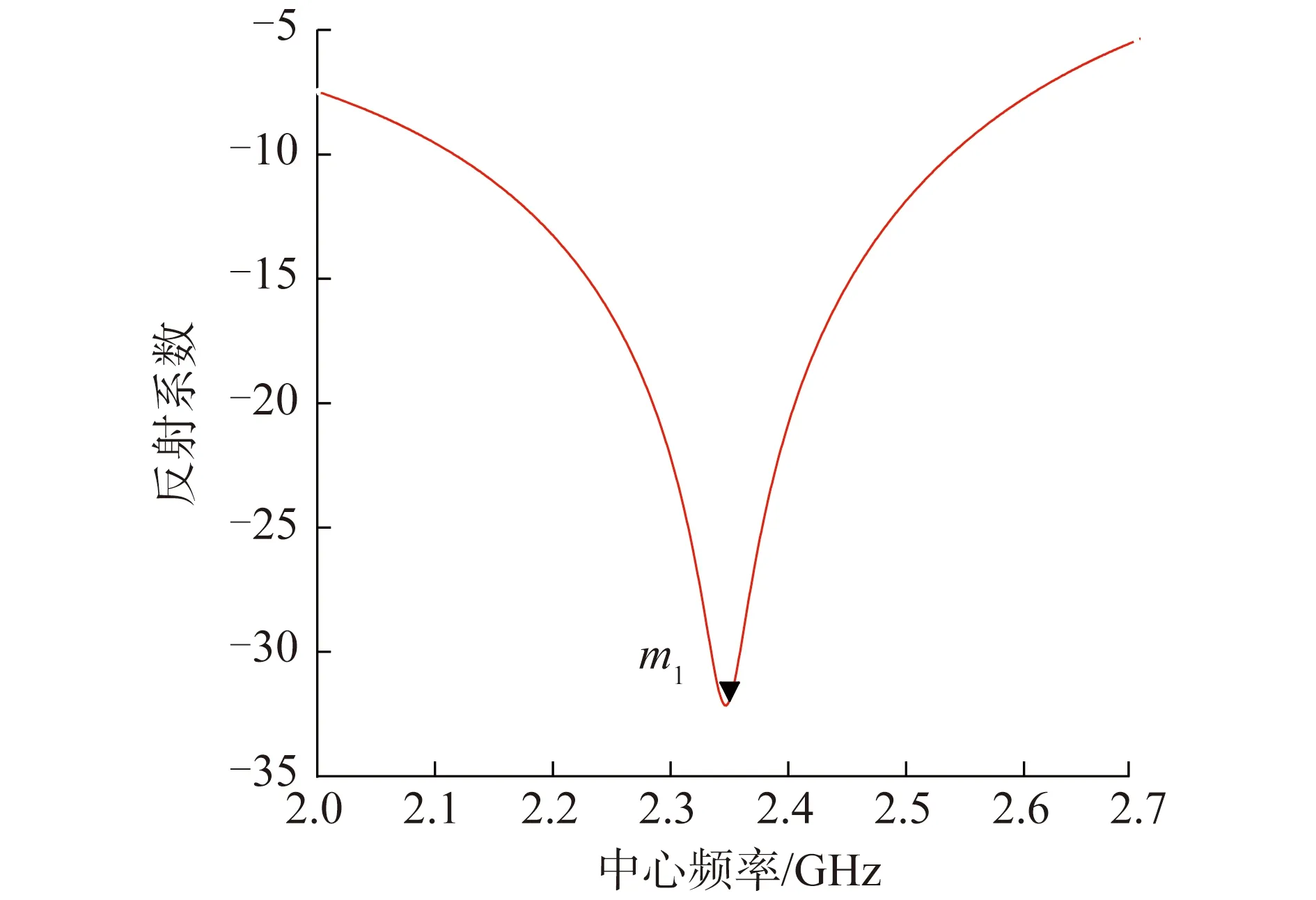
图4 源端与负载端匹配后的S参数ADS仿真Fig.4 Simulated S-parameter results via ADS after the source and the load ends are matched

2 解耦匹配微带电路HFSS设计仿真

基于本文关解耦匹配网络方面的理论分析，本文以LTE系统中的E频段中心频点即2.35 GHz为例，设计了带有解耦与匹配网络的双单极子微带天线实例，其结构如图5所示。该天线阵列由接地板、2副印刷单极子天线和介质材料构成。印刷单极子微带线的长度La=21.5 mm，宽度wd=1.5 mm；接地板尺寸为30.75 mm×25.8 mm；介质基板的尺寸为48.8 mm×30.75 mm。两天线间距为d=18.75 mm，对于中心频率2.35 GHz来说，这个间距相当于0.147λ0(λ0为中心波长)，由于间距太小，2副天线之间耦合效应严重。

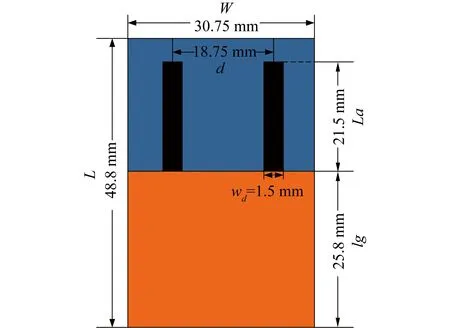
图5 紧凑型二元微带天线阵列结构图Fig.5 Structure diagram of the two-element compact microstrip antenna array

3 仿真与测试结果分析

3.1 仿真结果分析

通过对原始未解耦天线进行HFSS仿真可得到如图(6)所示的S参数；从图(6)的仿真结果可以看出，当天线间距为0.147λ0时，自反射系数S11达到-19.69 dB，说明天线端口的匹配已经基本良好。但是由于2根天线之间的距离非常近，在2.35 GHz时的交叉反射系数S21为-6.16 dB，这说明天线之间存在较强的耦合。为了抑制耦合，需要添加解耦电路。由本文理论分析知道，解耦之前首先需要利用微带线计算工具TxLine求出移相微带线的长度；从HFSS仿真结果中读出中心频率2.35 GHz时的S21值为0.429e-j108.39，也就是对应式中的α=0.492和φ=108.39°。令k=0，则2θ-φ=π/2，求得θ=99.20°，通过TxLine计算出来移相微带线长度为19.19 mm。为了最终实现去耦的目的，还需求出去耦元件的理论值，由式(11)知，去耦元件是电感元件。其中已知α=0.492，中心工作频率为2.35 GHz，将其代入式(11)中即可求出电感的数值为：

(12)

根据式(11)计算出电感的数值是4.27 nH，将该数值代入ADS中，得到ADS仿真仅去耦天线的S参数如图7(b)所示。从图中仿真结果可以看出，在2.35 GHz时的S21为-28 dB，说明ADS仿真去耦效果很好，达到了预期目标。随后再将此ADS得出的结果应用到HFSS仿真中，并优化去耦电感数值，得到HFSS仿真仅去耦天线的S参数如图7(a)所示。从图7(a)中可以看到，加入去耦电感后天线端口之间的耦合系数S21变得很弱，在2.35 GHz频率处的S21为-22.84 dB，相比较未加入去耦网络，其隔离度改善了17 dB左右，这说明去耦元件的添加极大地改善了端口之间的隔离度。不过去耦元件的引入也带来了端口不匹配的新问题，这可以从图中S11和S22的数值都变得比较大看出来，所以还需要在去耦之后另添加额外的单枝节匹配网络来修正去耦带来的端口不匹配问题。图8 分别为HFSS和ADS仿真去耦匹配后的S参数图。从图8(a)可看出，匹配后在2.35 GHz谐振频率处，S11值降低为-34.40 dB，说明天线端口间达到良好匹配；同时S21约为-20.90 dB，说明去耦效果并未因为匹配网络的加入而受到太大影响，仍保持较好的端口隔离度。可见通过去耦及匹配后，天线端口不仅达到了良好匹配，还实现了去耦的效果。

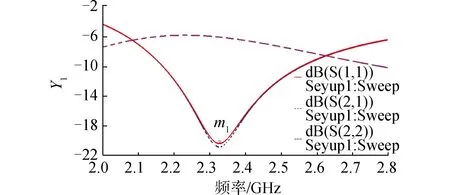
图6 HFSS仿真原始天线S参数Fig.6 Simulated S-parameters via HFSS for original antenna

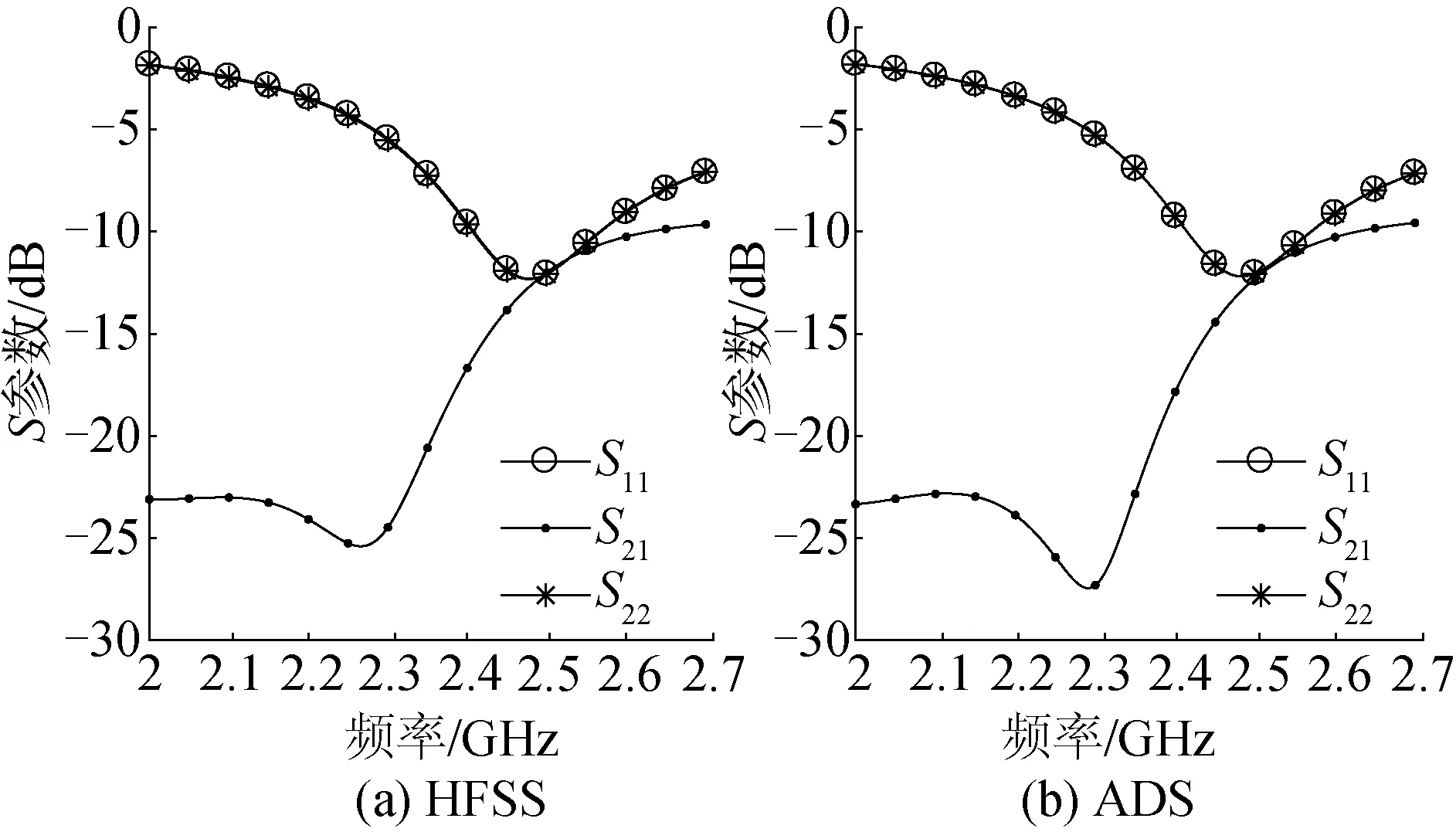
图7 HFSS和ADS仿真仅去耦天线的S参数Fig.7 Simulated S-parameters via HFSS and ADS for only decoupling antennas

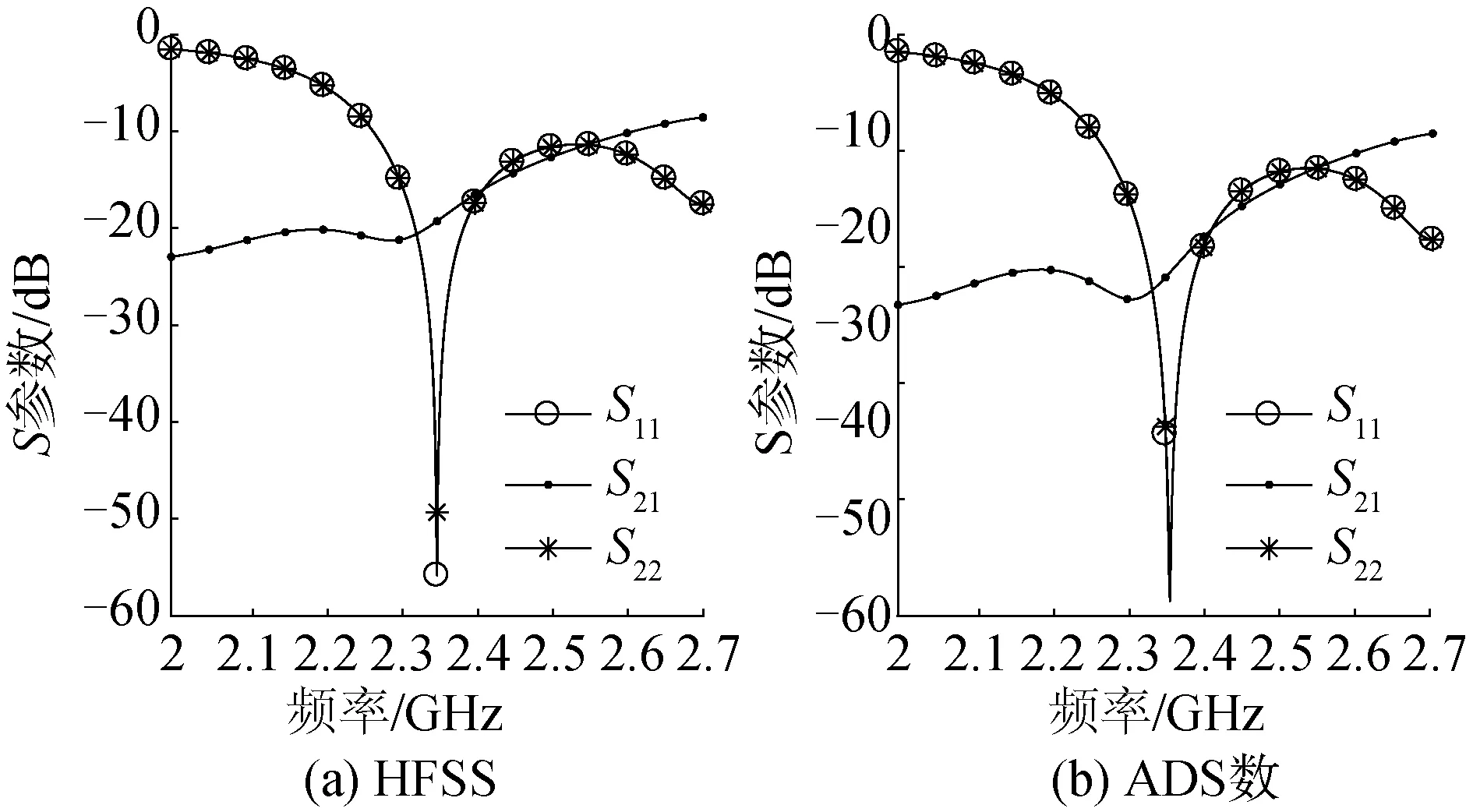
图8 HFSS和ADS仿真去耦匹配天线的S参数Fig.8 Simulated S-parameters via HFSS and ADS for decoupling and matching antennas

3.2 硬件电路测试结果分析

根据上一节的HFSS天线布局仿真分析，将所设计的紧耦合MIMO双天线系统进行了PCB板实物制作，制作的天线实物图如图9所示。

图9 天线实物图Fig.9 Photograph of the fabricated printed circuit board dual-monopole antenna array

将原始未解耦天线标记为1号板，仅去耦天线标记为2号板，去耦及匹配天线标记为3号板。其中，原始天线的实测和理论S参数如图10所示。可以看出，实测的原始天线S参数与理论仿真结果基本一致。在所设计的频段内，天线之间耦合效应较强，在中心频率处的实测S21为-5.61 dB，也就是说大部分能量被耦合到了临近天线中。为了达到抑制耦合效果，图9(b)给出了所制作的仅去耦PCB板天线。从图9(b)中看到，二元天线之间焊接了抑制耦合电感元件，仅去耦天线的实测及理论对比S参数如图10(a)所示。

从图10(a)可以看出，在二元天线之间添加抑制耦合元件之后，天线之间的耦合效应被明显抑制，实测天线的S21为-24.93 dB，与未去耦时相比改善了19.32 dB。还可以看出，尽管抑制耦合电路消除了天线之间的耦合，但是也引起了天线各自的输入阻抗失配，谐振点发生偏移。所以，在去耦合之后还要另加入匹配网络以调节天线谐振点。图9(c)是加入解耦网络与匹配网络之后的实物图。图10是去耦匹配天线的实测及理论对比S参数图。

从图10的仿真结果可以看出，解耦网络达到了预期紧凑型双天线系统的解耦效果，天线S21参数符合实际工作天线要求。频率2.43 GHz处的实测S21为-24.62 dB，S11为-21.86 dB；S21的-20 dB带宽范围为2.3～2.43 GHz，是中心频率的5.53%；同时匹配电路将天线谐振点修正到了所要求的工作频段内，S11的-10 dB带宽范围是2.29～2.48 GHz，是中心频率的8.09%，达到了实际电路的去耦匹配要求，这些都进一步验证了理论分析设计的正确性。

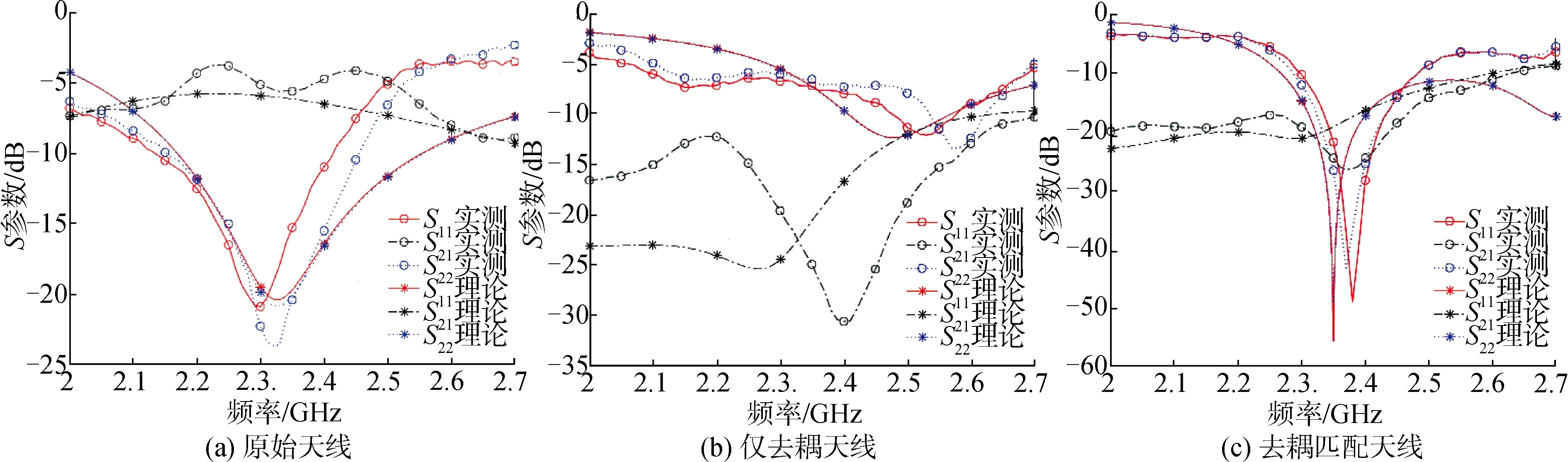
图10 天线的实测和理论S参数对比Fig.10 The comparison of measured and theoretical S-parameters of antennas

4 结论

1)基于经典微波端口散射和导纳矩阵理论，针对二元紧耦合MIMO系统，进行有关天线阵元间解耦元件设计理论值的分析与计算是可行的；以该理论值为初始值，通过HFSS和ADS混合仿真进行适当优化，即可设计出最终的抑制耦合共轭匹配微带电路方案。

2)通过HFSS仿真输出的微带电路布局图制作的二元微带紧耦合天线阵、仅解耦天线阵、以及耦合抑制匹配网络天线经现场测试，与计算机数值仿真结果非常吻合；说明理论分析与计算过程正确可靠，本文所给出的相应设计方案工程实现可行。

本文工作将为紧耦合MIMO系统的去耦天线设计提供一定的理论指导；鉴于5G系统已采用大规模MIMO天线阵，故后续可以围绕更多元天线阵的紧耦合MIMO系统开展相关研究工作。