三维各向异性梁结构等几何振动分析

高晟耀，王雪仁，唐宇航

(中国人民解放军92578部队，北京 100161)

相比于各向同性结构，各向异性结构[1-6]由于拥有高刚度比和强韧性等特点而被广泛应用于各种工程领域中。三维各向异性曲梁和直梁的振动特性分析一直是振动噪声控制领域的热门课题[7-21]。学者利用各种数值计算方法对三维直梁和曲梁进行结构建模和动力学特性分析，如传统有限元法，动刚度法、傅里叶法等。然而，大部分的数值方法在计算曲梁时很难保证结构几何的精确性和高阶函数连续等问题。等几何方法[22]是一种能够实现计算机辅助设计(computer aided design，CAD)与计算机辅助工程(computer aided engineering，CAE)的无缝连接，并具有很高的精确性的数值方法。由于该方法具有高精度，高收敛，网格细化方便与高阶函数连续性等优点而被应用于求解各复合的梁、板和壳的力学问题[23-31]。本文针各向异性的直梁和曲梁结构，并基于三维弹性理论，采用非均匀有理B样条(non-uniform rational B-spline，NURBS)函数，同时结合有限元思想进行几何建模和振动分析。通过一系列的数值算例验证该方法计算三维各向异性直梁和曲梁振动特性的快速收敛性与良好的精确性，同时还分析了不同边界下的参数影响。

1 三维各向异性梁

如图1所示为三维各向异性梁结构，其中a、b和h分别为梁的长、宽和高。笛卡尔坐标选择建立在三维梁的轴向起始面。

图1 三维各向异性梁模型Fig.1 Model of three dimensional orthotropic beam

基于三维弹性线性方程，各向异性梁的正应力和切应力可表示为:

(1)

(2)

式中：带逗号的下角标x、y、z表示相应的位移分量的一阶偏导数；u、v和w分别为x、y和z方向上的位移分量；Cij(i,j=1,2，…，6)为弹性材料系数，其具体表达式为：

(3)

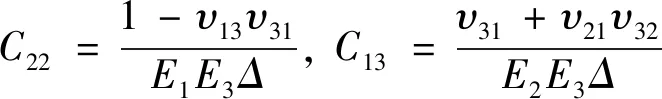
(4)

(5)

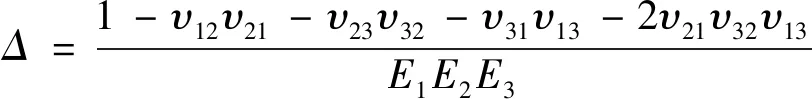
(6)

C44=G23，C55=G13，C66=G12

(7)

式中：E1、E2、E3为3个方向上的杨氏模量；υij为泊松比，其满足以下方程：

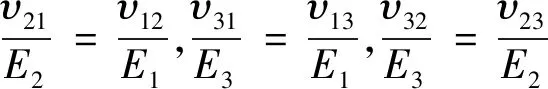
(8)

2 三维等几何有限元

2.1 非均匀有理B样条基函数

设节点矢量E=(ξ1,ξ2,ξ3,…,ξn+p,ξn+p+1)，ξi(i=1,2，…，n+p+1)为非负不减参数。则B样条的表达式[32]为:

1)p=0:

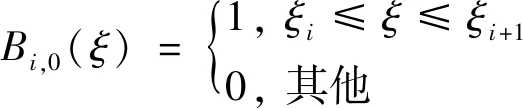
(9)

2)p>0:

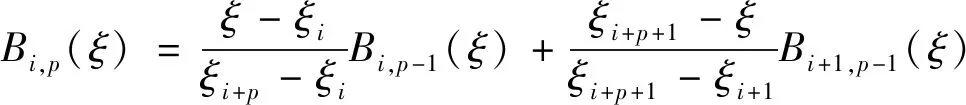
(10)

式中：p为基函数的阶数；n为基函数总数。基于节点矢量E=(0,0,0,0.5,1,1,1)的2阶的B样条函数如图2所示。

图2 基于E=(0,0,0,0.5,1,1,1)的B样条函数Fig.2 B-splines functions based on E=(0,0,0,0.5,1,1,1)

在实际的建模仿真中，B样条函数并不能很好的满足工程设计师的要求。通过对每个B样条函数引入相应的权值，可以构建非均匀有理B样条函数(NURBS),其一维函数表达式为：

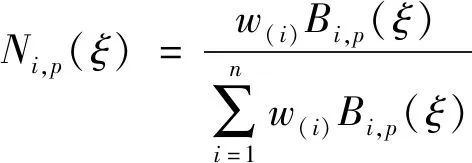
(11)

式中：Bi,p(ξ)为B样条函数；wi为相对应的权值。三维的NURBS为：

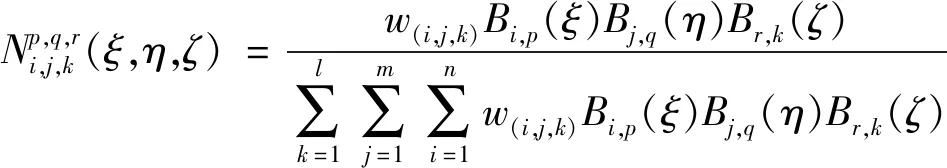
(12)

式中：Bi,p(ξ)、Bj,q(η)、Br,k(ζ)为3个参数空间上的B样条函数；w(i,j,k)为对应的权值。

2.2 三维等几何振动控制方程

在三维等几何分析中，采用有限元思想，将作为形函数对未知位移分量的NURBS样条函数：

(13)

式中a=i+(j-1)m+(k-1)ml;ua=(ua,va,wa)T为节点a的位移矢量；Na为控制点a的NURBS函数。

三维各向异性梁结构的势能U和动能T为：

τxyγxy)dxdydz

(14)

(15)

基于哈密尔顿原理，三维各向异性梁结构的虚功可表示为：

(16)

将式(1)～(6)代入式(16)，并结合有限元方法，三维各向异性梁结构的振动方程为：

[K-ω2M]u=0

(17)

式中：K和M分别为整体刚度矩阵和质量矩阵；ω为固有角频率；u为梁的控制点位移矢量。

3 三维梁等几何数值算例

通过前部分的理论推导和求解方法，本文将对各向异性的直梁和曲梁进行验证和数值结果的分析。并对异性的直梁和曲梁的参数变化对结构的振特性影响进行研究。

3.1 各向异性直梁数值结果

图3 各向异性直梁的频率收敛性Fig.3 Convergency of frequency of the orthotropic straight beams

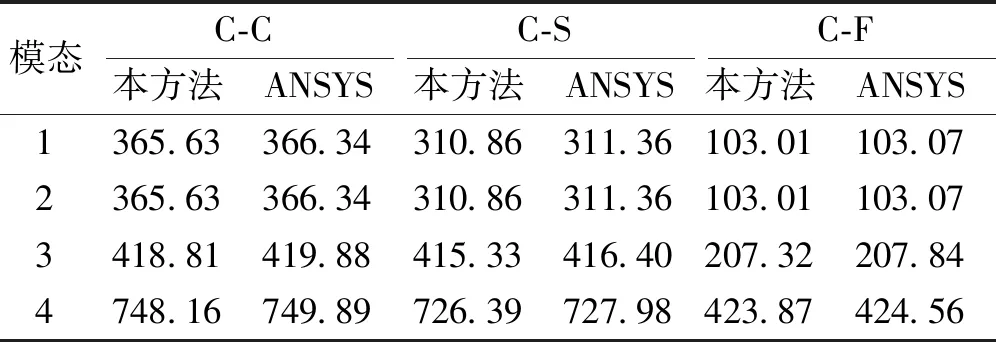
表1 各向异性直梁的频率f对比Table 1 Comparisons of frequencies f of orthotropic straight beams Hz

在本次对比中，梁结构的几何参数和材料属性与表1中相同。在ANSYS计算中节点的数目大于一定数值时，其计算结果收敛。通过仿真计算可知传统有限元计算该结构的前4阶固有频率在节点大于2 793才趋于收敛。通过图3可知，该方法计算结果在p=2时，控制点大于600收敛；在p=3时，控制点大于500收敛；在p=4时，控制点大于400收敛。可见该方法可通过提高函数的阶数，从而使计算效率优于传统有限元法。在本次对比分析中，ANSYS的数值结果采用SOLID45划分了24 696个节点计算而得。而本方法的数值结果采用p=q=r=3的NURBS并结合10×4×4单元(控制点=637)计算而得。通过数据对比可以看出，该方法计算出的振动频率与ANSYS的计算结果能很好的吻合。从而验证了该方法具有很好的精确性。

图4为边界为C-S的各向异性直梁的前4阶模态图，进一步验证该方法计算三维各向异性直梁的精确性。该模态图计算所用的几何参数和材料参数与表1中的一样。从图4和表1可以看出直梁结构的第1阶频率与第2阶频率相等。这是因梁的宽和高是相等的，且该结构的宽和高2个方向的材料属性也是相等的。因而，在该参数下三维梁的第1阶模态图与第2阶一样，只是运动方向不一样。通过模态图的对比，可以验证该方法不仅能够精确计算三维各向异性梁结构，同时也能精确的描述梁的振动模态。

图4 C-S边界下各向异性直梁的频率收敛性Fig.4 Convergency of frequency of the orthotropic straight beams with C-S boundary condition

为了更好地分析几何参数对各向异性梁的频率影响，在本次分析宽度b=0.3 m，长度a=1 m，厚度h为变量。材料参数保持与收敛性分析一样。图5给出了长厚比对三维各向异性梁结构的前4阶无量纲频率的影响。通过图5可以看出，不管在什么边界下，三维各向异性直梁结构的固有频率随厚度的增加而增加。当直梁的厚度增加时，会导致其在长度方向的抗弯刚度急剧增加。从而三维直梁的固有频率增加。当厚度h从0.05 m增加到0.125 m时，三维直梁的第3阶固有频率并没有变化，其原因有可能是该振动模态主要沿宽度方向振动。

图5 厚长比h/a对前4阶无量纲频率的影响Fig.5 Effects of thickness-to-length ratio h/a on the first four non-dimensional frequencies

3.2 各向异性曲梁数值结果

通过前文分析，可以看出该方法计算直梁频率的可靠性和精确性，然而在实际工程中，曲梁的应用比直梁更加广泛。曲梁的材料参数保持不变：E1=40E2，E2=E3=2 GPa,G23=0.5E2,G13=G12=0.6E2,υ12=υ13=υ23=0.25,ρ=1 500 kg/m3。曲梁的结构模型如图6所示。

图6 三维各向异性曲梁模型Fig.6 Model of three dimensional orthotropic curved beam

图7为三维各向异性曲梁无量纲振动频率的收敛性，该收收敛性分析结构的边界、NURBS的阶数和几何划分的单元与直梁分析一样。曲梁的几何参数为：a=1 m，b=h=0.1 m,R=1 m。从图7可以看出该方法计算曲梁时也拥有快速收敛的特性。表2给出了三维各向异性曲梁的频率对比。ANSYS的数值结果采用SOLID45划分了25 872个节点计算而得。本方法的数值结果采用p=q=r=3的NURBS并结合10×4×4单元(控制点=637)计算而得。通过表2可以看出该方法计算曲梁与ANSYS计算的曲梁频率结果也能吻合。表2中的曲梁频率的误差比表1中直梁的误差大，是因为ANSYS对曲面划分网格与本方法差距所造成的。图8为三维各向异性曲梁在C-S边界下的前4阶模态对比图。从图中可以看出曲梁的模态对比图与ANSYS计算的模态图能很好地吻合。

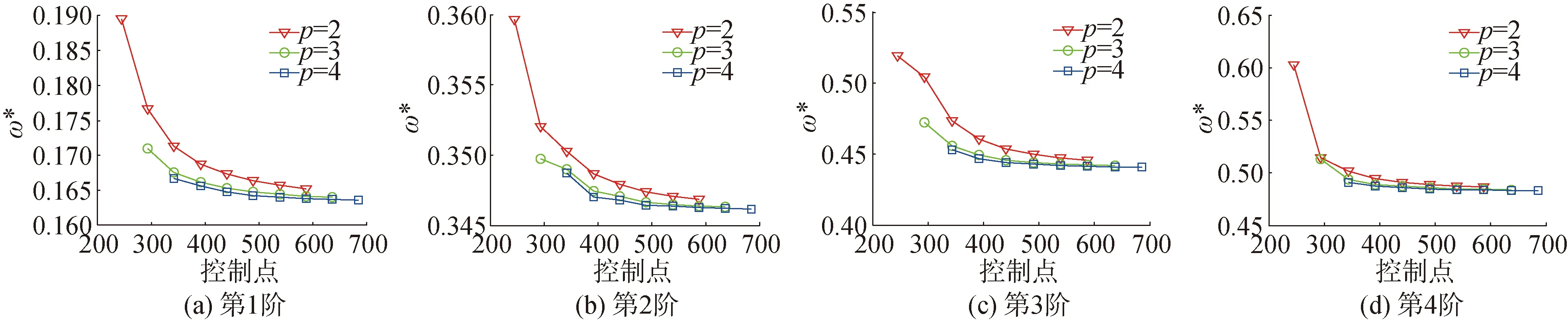
图7 各向异性曲梁的频率收敛性Fig.7 Convergency of frequency of the orthotropic curved beams

图8 C-S边界下各向异性曲梁的频率收敛性Fig.8 Convergency of frequency of the orthotropic curved beams with C-S boundary condition

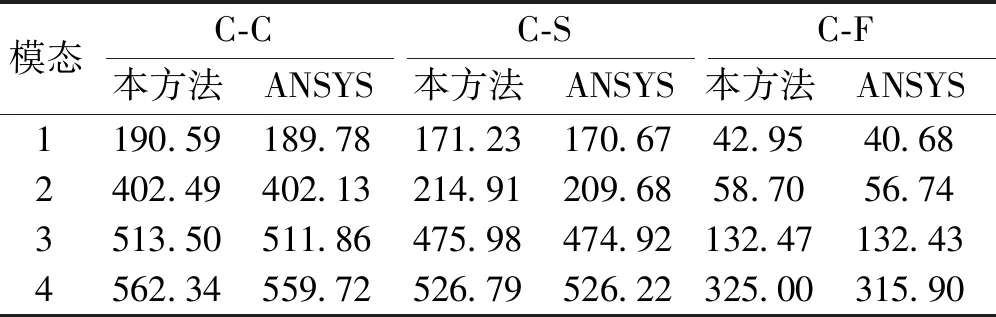
表2 各向异性曲梁的频率f对比Table 2 Comparisons of frequencies f of orthotropic curved beams Hz

图9为厚度变化对三维各向异性曲梁无量纲固有频率的影响。在该分析中，材料参数保持不变。几何参数设置为a=1 m;b=0.1 m;R=0.1;从图9可以看出，三维各向异性曲梁的无量纲频率在整体上随厚度的增加而增加；无量纲曲线的斜率随厚度的增加而减小。部分无量纲频率在一定范围内随着厚度的增加有可能保持不变，或者缓慢减少，如图9中的C-C边界下的第2阶模态；C-C、C-S、S-S边界下的第3阶模态等。图10为曲梁半径变化对三维各向异性曲梁的无量纲固有频率的影响。在该分析中，除了厚度h和半径R外，三维各向异性曲梁的材料参数和几何参数设置与图9一样。曲梁的厚度h=0.1 m。从图10可以看出，半径R对三维各向异性曲梁的无量纲固有频率的影响与厚度相似。即除了三维各向异性曲梁的部分频率在一定范围内不一定随半径的增加增加；但在整体上，三维各向异性曲梁的无量纲固有频率随半径增加而增加。

图9 厚长比对前4阶无量纲频率的影响Fig.9 Effects of thickness-to-length ratio h/a on the first four non-dimensional frequencies.

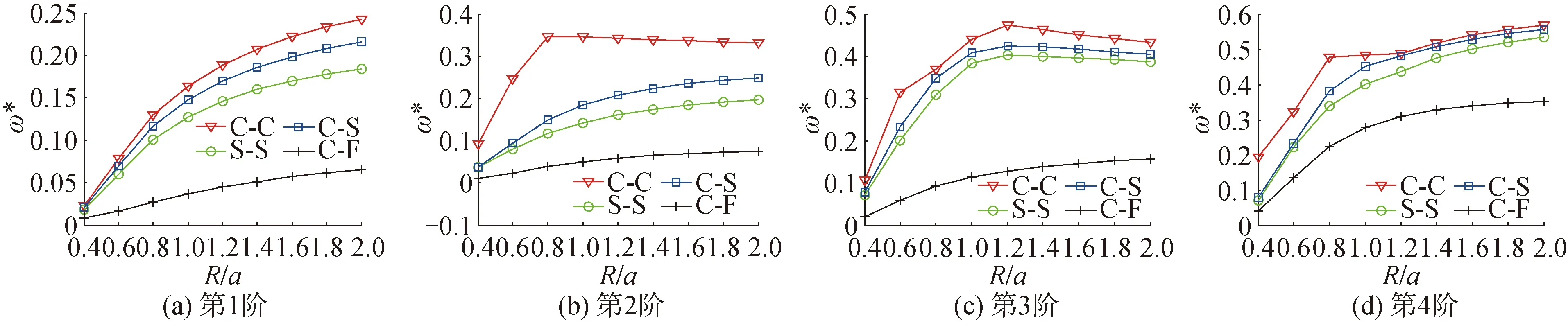
图10 径长比对前4阶无量纲频率的影响Fig.10 Effects of radius-to-length ratio h/a on the first four non-dimensional frequencies

4 结论

1)该方法在计算三维各向异性梁时具有快速收敛性，且基函数的阶数越高，计算结果收敛速度越快。

2)该方法具有良好的精确性；其计算曲梁的固有频率与传统有限元结果吻合度低于该方法计算直梁固有频率和传统有限元结果的吻合度。

3)边界约束越强，固有频率越高；随着半径的增加，曲梁的前四阶固有频率增加；整体上固有频率随着厚度的增加而增加，但部分阶次的固有频率有可能不变。

4)借助NURBS强大的几何建模能力，该方法还适用于求解更为复杂的三维曲梁结构。