正交各向异性梁结构自由振动分析
2020-07-28刘瑞杰王雪仁贾地
刘瑞杰,王雪仁,2,贾地
(1.中国人民解放军92578 部队,北京 100161;2.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨,150001)
梁结构广泛应用于船舶与海洋工程、建筑工程和航空航天等领域中,对于此类结构的振动特性及其参数影响规律研究受到科研工作者的广泛关注[1-11]。随着材料技术和加工工艺的进步,复合材料由于自身比刚度大、可设计性强、机械性能突出等优点,成为了工程应用中的首选材料。复合材料往往呈现出较为明显的正交各向异性,对各向异性梁结构动力学特性的研究具有十分重要的意义。经典的梁理论模型主要包含Euler-Bernoulli和Timoshenko 2种理论。然而,欧拉-伯努利梁理论忽略了结构横向拉伸和剪切变形以及转动惯量的影响,其计算结果与实际情况相比存在较大误差。铁木申科梁理论虽然考虑了横向剪切变形和转动惯量的影响,但其引入的剪切修正因子对梁结构的几何截面形状和材料参数均具有较高的依赖性,故而不适用于复合材料梁结构的研究。另外,经典梁理论更多地关注于梁结构沿着特定方向上的形变或振动问题。当梁结构的长径比较小或截面为不规则形状时,梁结构在外界载荷作用下不仅会出现弯曲变形,亦会产生扭转、拉伸或弯扭组合变形。此时需寻求具有较高计算精度和适用性的三维理论。Carrera等[12]基于卡诺统一定理提出了一种改进的高阶梁理论模型。该理论将梁结构的位移容许函数分解为截面和轴向2部分,利用高阶泰勒公式拟合梁结构的截面位移,从而以泰勒展开的阶次控制理论的计算精度。该理论模型也被成功地应用于求解一些复杂问题,如薄壁结构、复合材料问题、旋转叶片等[13-16],并展现出较高的计算精度。
本文结合卡雷拉理论(Carrera unified formulation,CUF)和有限元理论建立正交各向异性梁结构的三维振动分析模型。基于梁结构的应变能和动能,由最小势能原理推导梁单元的质量矩阵和刚度矩阵。分别从质量和刚度矩阵中提取出3×3阶的质量、刚度核心矩阵,利用循环得到整个梁的质量矩阵和刚度矩阵。随后对多种边界条件下各向异性梁结构进行了自由振动分析,并将计算结果与有限元分析软件结果对比分析。
1 正交各向异性梁三维理论模型
1.1 梁结构位移场离散
如图1所示,考虑一矩形正交各向异性梁结构,建立直角坐标系(x,y和z)。正切轴x与生长环相切,纵向轴y与纤维方向平行,径向轴z与生长环垂直。梁形结构上任意一点沿坐标x,y和z3个方向上的位移变形分别用Ux,Uy和Uz表示。梁结构的长度为L,宽度和高度分别为b和h。

图1 正交各向异性梁结构示意Fig.1 The dimensions of an orthotropic beam
为了简化三维实体模型,本文通过分离变量将梁形结构的位移函数分为截面位移函数和轴向位移函数2个部分。其中,利用卡诺高阶理论对梁结构截面面内位移进行拟合,卡诺高阶理论中用到的二维泰勒展开分量可以简写为统一的形式。泰勒展开的阶次可直接控制该方法的计算精度。梁结构的位移函数为:
(1)
式中:N为二维泰勒展开的阶次;Γ为二维泰勒展开的总项数;Fτ表示泰勒展开中的第τ项;变量uxτ、uyτ和uzτ为梁形结构的轴向位移变量,是关于轴向y的函数。
轴向位移变量uxτ、uyτ和uzτ利用有限元方法进行轴向解域离散,可表示为:
(2)
以2节点线性梁单元(M=2)为例,函数为:
(3)
将式(2)代入式(1)中,梁结构的位移函数为:
(4)
通过式(4)可以看出,对于任意一梁单元,每一节点有3×Γ个未知变量,用向量表示为:
q=(A11,B11,C11,…,AΓ1,BΓ1,CΓ1)T
(5)
值得注意的是,通过增加分析中所使用的线性单元的数目,或使用高阶的插值函数,都能够提高有限元结果的精度。
1.2 梁结构自由振动控制方程
考虑结构发生微小变形,根据应变位移关系可得:
(6)
根据广义胡克定律,正交各向异性结构的应力应变关系可表示为:
(7)
正交各向异性材料的弹性系数可表示为[17]:
(8)
(9)
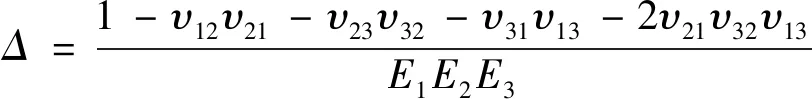
(10)
另外,υij和υji存在以下关系:
υijEj=υjiEi
(11)
如此,需要由9个独立参数来确定正交各向异性材料的物性参数:E1、E2、E3、G12、G13、G23、υ12、υ13、υ23。
基于能量法推导梁单元的刚度矩阵梁单元的应变能:
(12)
式中:ε为应变向量;σ为应力向量;K即为梁单元刚度矩阵。仔细观察方阵K的内部构造可以发现,该方阵是由一个3×3阶方阵Kijτs堆积而成,其中的9个组成部分如下:
(13)
(14)
(15)
式中:〈FτFs〉Ω表示截面内积分;〈NiNj〉l表示轴向单元内积分。当梁结构的厚度较小时,此处的有限元方法会产生剪切自锁现象,本文用低阶的高斯-勒让德数值积分消除此处的剪切自锁现象[18]。
梁单元的动能由各连续质点的动能累加而成:
(16)
式中:ρ为梁的密度;u′为梁上任意一点的速度,是关于时间t的函数。将位移函数代入上式中,则:
(17)
与刚度矩阵相似,Mijτs为质量矩阵的核心,质量矩阵可由3×3阶方阵Mijτs堆积而成,其中的9个组成部分如下:
(18)
采用划行化列、赋大数等有限元边界施加方法处理正交各向异性梁结构的边界条件,正交各向异性梁自由振动控制方程可表示为:
(Kz-ω2Mz)q=0
(19)
式中:Kz为梁的总刚度矩阵;Mz为总质量矩阵。
2 正交各向异性梁自由振动分析
本文通过对一正交各向异性梁结构的自由振动分析来验证本文模型的合理性。考虑梁结构的材料为正交各向异性材料,其材料属性可表示为:E1=145 GPa,E2=9.6 GPa,G12=G13=4.1 GPa,G23=3.4 GPa,υ12=0.3,密度ρ=1 389 kg/m3。为了方便与文献[19]对比,纤维方向角取为90°,梁结构的长高比取为10,考虑两端固支边界条件,并引入无量纲频率参数:
(20)

表1给出了正交各向异性梁结构的前6阶弯曲模态的无量纲频率参数对比结果。本文计算结果与文献[19]结果具有较好的一致性。值得注意的是,本文所建立的梁结构理论模型为三维模型,不仅可以预测梁结构的横向弯曲振动,也可以获得梁结构的扭转模态和纵振模态。
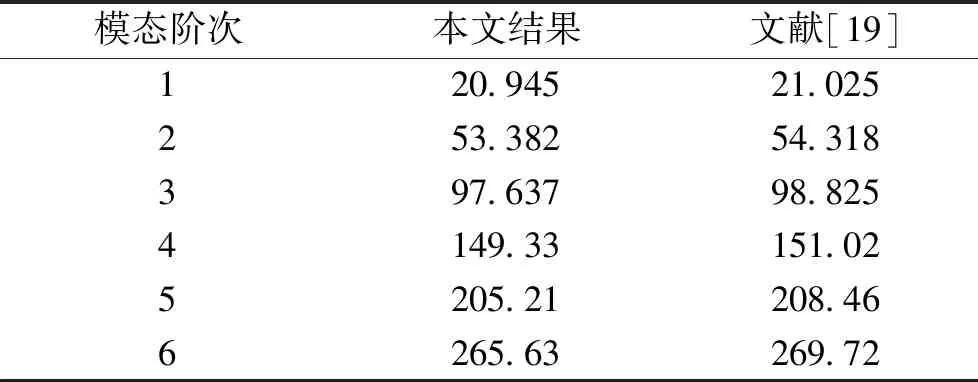
表1 正交各向异性梁前6阶弯曲模态的无量纲频率参数Table 1 First six non-dimensional frequencies of bending modes of an orthotropic beam
为了进一步验证本文三维振动分析结果的收敛性和正确性,本文将与有限元商业软件ANSYS的三维仿真结果进行对比。选取梁结构材料(graphite fabric-carbon matrix layers,GFCML),其材料属性可表示为:E1=173.1 GPa,E2=33.1 GPa,E3=5.17 GPa,G12=9.38 GPa,G13=8.27 GPa,G23=3.24 GPa,υ12=0.036,υ13=0.25,υ23=0.171,密度ρ=1 650 kg/m3。令梁结构的宽度和高度相等b=h=0.2 m,长度L为2 m。为了较为准确地预测梁结构的扭转模态,本文选取截面拟合多项式的阶次N为4。
表2为正交各向异性梁结构在简支边界条件下,前10阶模态的收敛情况,每一行代表结构不同的模态阶次,每一列代表着不同的单元类型和单元数。B2表示2节点线性单元,B3表示3节点抛物线单元。从表中可以较为清楚地看到随着单元数量的增加,本文方法的计算结果快速收敛至稳定值。选用较高的单元类型会进一步加快计算方法的收敛速度。同时,表2也列出了利用ANSYS软件计算出的数据,对于该仿真结果,本文选用了SOLID186单元类型,划分640个单元,3 665个节点。其有限元网格划分结果如图2所示。另外,2种计算方法所需的自由度数(DOFs)均在表2中给出。通过对比可以发现,本文方法所需较少的自由度数而获得与ANSYS相近的计算结果。

表2 简支边界下正交各向异梁结构前10阶模态收敛性分析Table 2 Convergence of the first ten modes of an orthotropic beam with simple boundary condition Hz

图2 有限元网格划分结果Fig.2 Mesh dividing results of the finite element method
表3为3种经典边界条件(简支、悬臂和固支边界)下正交各向异性梁结构的前10阶固有频率。通过与ANSYS仿真结果的对比,可以发现,对于不同的约束条件,本文方法均具有较高的计算精度。另外图3给出了简支边界条件下正交各向异性梁结构的振型图,图3(a)~(c)为ANSYS仿真结果,图3(d)~(f)为本文方法绘制的结果。(a)和(d)为梁结构第1阶弯曲振型,(b)和(e)为结构1阶扭转振型,(c)和(f)为结构第1阶纵振振型。可以看出本文方法不仅可以用于预测正交各向异性梁结构的弯曲模态,也可以较为准确地预测梁结构的扭转模态和纵振模态。
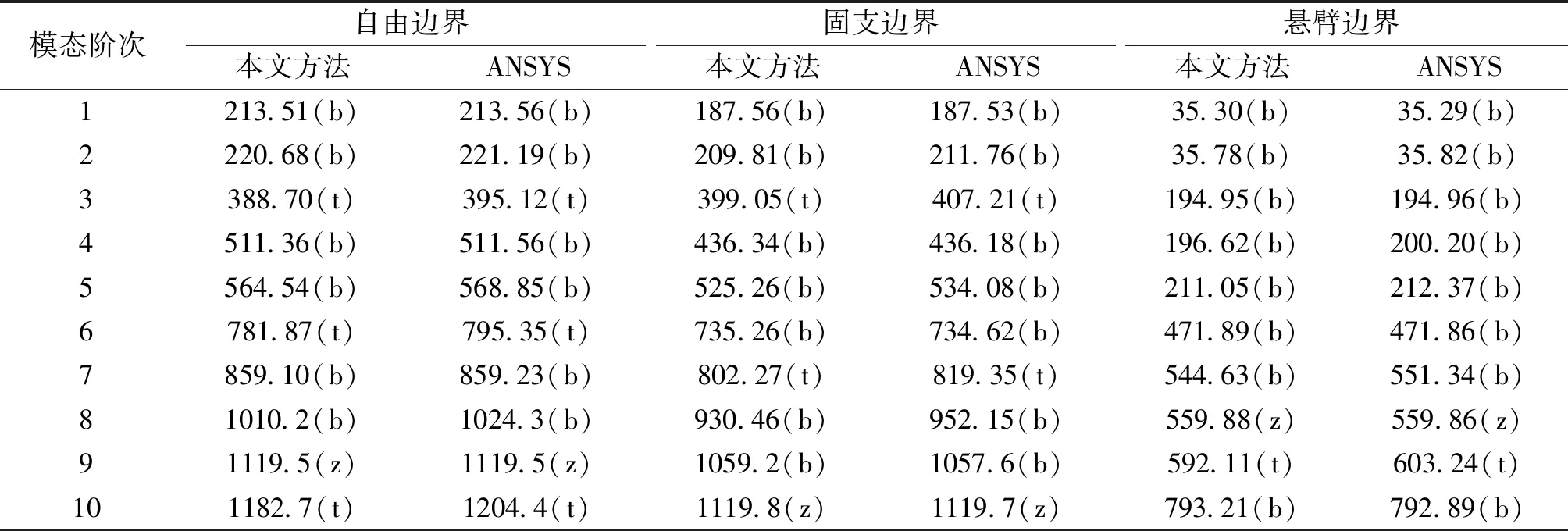
表3 正交各向异性梁结构不同边界条件下的前10阶固有频率分析结果Table 3 Frequency of first ten modes of an orthotropic beam with different boundary conditions Hz

图3 简支边界条件下正交各向异性结构的三维振型图Fig.3 Three-dimensional mode shapes of an orthotropic beam with a simple boundary condition
3 结论
1)本文方法不仅可以提供高精度的解,还可以较为全面地展现其振动特性(弯曲模态、扭转模态、纵振模态)。
2)本文方法所需较少的自由度数而获得与商业有限元相同的计算精度。
3)对于正交各向异性梁结构的几何参数设计及动力学特性优化具有指导意义。
