基于L0范数的Retinex图像增强算法*

陈茹霞,强振平,邵小锋,何丽波

(1.西南林业大学大数据与智能工程学院,云南 昆明 650224;2.云南警官学院信息网络安全学院,云南 昆明 650223)

1 引言

人的眼睛在对物体颜色进行感知时，无论外界光照环境怎样变化，都能保持相对不变，这种现象称为色彩恒常性[1]。例如：红色在强光下表现为鲜红，在弱光下表现为暗红，但不能表现为黄或者绿。对于色彩恒常性，Land等人[2]经过多年的研究，提出了著名的视网膜大脑皮层理论——Retinex理论。Retinex是由单词Retina(视网膜)和单词Cortex(大脑皮层)的缩写组合而成的。该理论认为物体的性质是由它的反射能力决定的，而不是反射的强度[3,4]。Retinex理论形成的基础是颜色恒常性理论，目前Retinex算法普遍应用于图像处理，包括图像增强和图像恢复[5,6]。该算法主要研究如何增强外界物体的入射光的照射分量L(x,y)，从而获得图像的本质特性。

Retinex理论的基本假设是人的眼睛所观察到的图像I(x,y)是由入射光L(x,y)(外界物体表面入射光)和反射图像R(x,y)(物体表面的反射性质)所决定，其数学表达为：

I(x,y)=L(x,y)R(x,y)

(1)

图像增强技术的目的在于获取图像中的重要部分，抑制非重要的部分，从而改善图像的视觉效果，达到目标需求[7]。目前图像增强主要包括空间域增强和频率域增强。例如，直方图均衡化、Gamma校正、线性拉伸、小波变换等，对于不同的图像，使用不同的图像增强算法在取得一定效果的同时，也会出现各种问题[8 - 10]。比如，拉普拉斯算子可以增强图像灰度发生突变的部分，弱化灰度变化缓慢的部分，从而提取图像的高频信息，使轮廓更加清晰。但是，拉普拉斯算子在处理过程中也会增加图像的噪声，因此经常需要将拉普拉斯图像叠加到原始图像，以达到最终的锐化效果[11,12]。各向异性扩散滤波在计算机视觉和图像处理中有着广泛的应用。通过把图像当作一个热场来模拟传热过程，把每个像素都看作一个热流，用当前像素和周围像素进行扩散[13]，但迭代次数过多或者过少都会影响最终的结果。单尺度Retinex算法在图像处理中可以保持原始图像的亮度，但不能同时提高图像的对比度。经过增强后的图像会产生光晕现象，输出色彩失真[14]。多尺度Retinex算法可以兼顾图像的局部和全局的动态范围压缩，实现图像色彩增强，保持图像的本质特性，但与此同时会出现图像边缘锐化不足，纹理不清晰，高频区域突出不明显等问题[15 - 17]。

本文通过分析Retinex算法的特点，结合L0范数图像处理算子，提出一种新颖的图像增强算法RIEALN(Retinex Image Enhancement Algorithm based onL0norm)，在提取图像边缘信息的同时减少图像噪声，实现图像增强。

2 相关工作与分析

2.1 多尺度Retinex算法

Retinex理论旨在从人眼观察到的图像I(x,y)中求得从物体表面的反射性质R(x,y)，从而将物体的本质还原出来[18]。采用对数运算，如式(1)所示：

LogR(x,y)=LogI(x,y)-LogL(x,y)

(2)

在文献[14]中，L(x,y)由原始图像I(x,y)与高斯函数卷积而得，目的是为了获得图像的低频成分。L(x,y)的不同计算方法就成为了Retinex相关算法研究的重点。直接应用高斯函数卷积方法，就是单尺度Retinex SSR(Single Scale Retinex)算法，由式(2)可得：

RSSR(x,y)=logI(x,y)-log[F(x,y)*I(x,y)]

F(x,y)=λe-(x2+y2)/σ2

F(x,y)dxdy=1

(3)

其中,RSSR(x,y)为输出图像；I(x,y)为人眼所观察到的图像；F(x,y)为高斯函数(中心-环绕函数)；*为卷积；λ由归一化常量；常量σ表示高斯环绕尺度。采用高斯函数估算入射光照，获取原始图像的低频信息，从原始图像中减去低频信息，得到的就是图像的高频信息，可以很好地抑制图像的噪声[19]，但同时会导致图像色彩失真，对高频区域强化不明显。

多尺度Retinex算法MSR(Multi Scale Retinex)由不同尺度的SSR算法结果进行加权平均而得，其公式为:

(4)

其中,RMSR(x,y)是MSR算法下光照估计后的输出图像；I(x,y)是原始图像；N是高斯中心环绕函数的个数，当N为1时，MSR则会退化为SSR,一般来说，为了保证同时兼有SSR算法具有高、中、低3个尺度的优点，所以N取3；wn表示权重，一般为1/N,n表示尺度(即wn=1/3)。MSR容易导致边缘锐化不足，局部的色彩会出现失真的现象。

多尺度Retinex色彩恢复算法MSRCR(MSR Color Recovery)是在多尺度Retinex算法中考虑到不同颜色通道的影响，加入色彩恢复因子Ci(x,y)得到的，计算公式为：

RMSRCRi(x,y)=Ci(x,y)RMSRi(x,y)

(5)

其中：

(6)

(7)

其中，Ii(x,y)表示图像第i个色彩通道的像素值，j∈{R,G,B}表示j属于RGB颜色通道。

2.2 Retinex改进算法研究

本文分别对传统的Retinex算法和基于双边滤波的Retinex算法进行了分析，提出了基于L0范数的Retinex图像增强算法。

传统的Retinex算法采用高斯滤波函数估计图像的光照信息。高斯函数是一种中心-环绕图像滤波函数，高斯函数采用低通滤波，增强后的图像可获得图像的高频分量，虽然可以实现图像增强，但也会导致图像边缘模糊，整体亮度过高等问题[20]。

双边滤波Retinex算法实际上是一种各向异性的图像处理算法，它同时考虑了图像的空间邻近性和像素值的相似性，然后折衷处理，它的加权系数取决于空间核和距离核，可以很好地实现图像平滑与轮廓保持[21,22]。基于双边滤波的多尺度Retinex算法，从不同方向的尺度计算图像像素值，即将传统的高斯函数F(x,y)算子替换成双边滤波算子G(i,j)[21]，如式(8)所示：

RSSR(x,y)=logI(x,y)-log[G(i,j)*I(x,y)]

(8)

该算法可以很好地兼顾图像平滑与轮廓保持，但同时也容易造成图像细节丢失[21]。

Xu等人[23]于2011年提出了基于L0的梯度最小化模型，此后其广泛应用在图像处理领域中。L0范数是基于稀疏的图像平滑算子，通过计算全局小幅度的方法实现L0平滑，增加过渡的陡峭度，消除低振幅结构来强化主要边缘[24,25]。Retinex算法存在边缘模糊与纹理不清晰等问题，与L0范数的图像平滑算子结合实现图像增强将是本文研究的重点。

3 本文算法

3.1 光照图像估计

光照图像估计是Retinex图像增强算法的核心步骤[26]，也是本文重点改进的地方。光照图像估计方法的选择会直接影响图像的增强效果。本文采用基于L0范数的图像平滑算子来估计光照图像。

传统的Retinex算法采用高斯滤波在基于光照一致性的基础上估计图像光照，而在实际应用中，图像的光照强度并不是一致的，因此存在增强后的图像容易产生边缘模糊等问题。L0范数图像平滑算子主要通过控制产生非零梯度的数目，计算梯度的稀疏性以增强边缘，使轮廓可以更好地保留下来，同时以图像全局的方式平滑非重要的细节，实现图像平滑[27]。

L0范数是指在向量中不等于零的元素的数目。图像梯度L0范数可以表示为：

c(f):=#{p||fp-fp+1|≠0}

(9)

其中,p和p+1是相邻的元素，f表示输出信号，fp表示元素p的信号值，|fp-fp+1|为图像梯度，#{}表示计数，输出满足|fp-fp+1|≠0的个数，即c(f)。本质上c(f)是图像中非零梯度个数的函数，与图像的梯度的大小无关，只是一个约束条件，并不是目标函数。要实现图像梯度的最小化，需要同时考虑图像的一维信号和二维信号[28]。

对于一维信号，输入信号为g，输出信号为f，目标函数为:

(10)

式(10)可以很好地提取信号的显著的结构信息。目标函数是为了使输入信号和目标函数尽可能地接近，k′为非零梯度的个数约束，对于一幅图，k′的个数可能会取上千上万个。为了控制k′的数量,将式(10)转化为：

(11)

其中,λ′为权重，也是一个平滑参数，控制两者之间的比重，当权重的值越大时，就说明图像越平滑，而且图像中的c(f)(非零梯度个数)与1/λ′呈现出单调递增的关系。

梯度的度量表示为：

C(S)=#{p||∂xSp|+|∂ySp|≠0}

(12)

它计算了p的幅值|∂xSp|+|∂ySp|不为零的个数。

根据这个定义，S便可通过式(13)求解得到:

(13)

与一维信号相比，式(13)也能增强图像显著的结构信息,它的优势是无论k′怎么改变，图像的边缘都不会模糊。

3.2 基于L0范数的Retinex图像增强算法

基于L0范数的Retinex图像增强算法实质上是以L0范数图像平滑算子提取图像的轮廓，并通过与原始图像融合实现图像增强。全局L0梯度最小化方法限制非零梯度的数量，以提取图像的边缘信息。

基于L0范数的Retinex图像增强算法实现流程可以概括为：读取原始图像I(x,y)，对彩色图像中的rgb三通道分别进行L0范数图像平滑算子处理，权重(λ)对应高斯滤波函数中的高斯环绕尺度(σ)，通过增加不同的L0梯度最小化因子，在迭代的过程中确保不同尺度轮廓成分的均匀增强，实验中主要通过3个不同的通道来确保不同的尺度，分别做高、中、低尺度计算，值分别为0.01，0.005，0.001(均为经验值)[14]。提取出图像的轮廓，并与原始图像进行融合，以突出重要细节，抑制不重要细节，实现原始图像的增强。

图1为基于L0范数的图像轮廓提取效果。

Figure 1 Image contour extraction based onL0-norm图1 基于L0范数的图像轮廓提取

结合Retinex算法，通过3个不同的通道来确保不同的尺度，如图2所示。

Figure 2 Image contours extracted at different scales图2 不同尺度提取的图像轮廓

本文算法是基于L0范数的Retinex图像增强算法，致力于克服传统算法的缺陷，以便更好地实现图像增强。RIEALN算法流程如算法1所示。

算法1RIEALN

输入：原始图像I(x,y),

σ={0.01,0.005,0.001},//尺度

S1=2,//低值裁剪像素的百分比

S2=2,//高值裁剪像素的百分比

p=0.2。//图像融合中的经验值

输出：增强图像。

步骤1提取图像信息(尺寸：M′*N′，通道数：C)，初始化参数(a,i=1)。

步骤2估计光照图像，每个通道进行循环：

初始化参数σ_list=[]，L=length(σ_list),j=1；

使用L0范数梯度算子计算光照图像Lij；

使用SSR算法(式3)获得RSSR，输出图像平滑结果Ri。

步骤3使用MSR(式(4))提取图像增强成分。

步骤4图像融合：参数P*MSR+I。

该算法对应的流程图如图3所示。

Figure 3 Flow chart of RIEALN图3 RIEALN的流程图

4 图像增强算法评价和对比

4.1 增强效果主观评价

本文采用2组实验作对比进行主观评价。第1组分别对传统的Retinex算法(高斯滤波)、基于双边滤波的Retinex算法以及本文算法进行对比，图4为第1组不同算法的图像增强对比图。图5为图4所对应的直方图。

通过以上对比分析可知，传统的Retinex算法(高斯滤波)在图像增强中会导致图像亮度过高、边缘模糊、纹理不清楚等问题；基于双边滤波的Retinex算法，虽然有不错的效果，但是图像亮度集中的区间太小，导致对比度低，同时也增强了整个图像的噪声，没有达到最佳效果。

Figure 4 Image enhancement comparison among of the first group of different algorithms图4 第1组不同算法图像增强对比图

Figure 5 Corresponding histograms of images in figure 4图5 图4图像对应的直方图

本文基于L0范数的Retinex图像增强算法在图像处理中通过提取图像的高频信息，并与原始图像融合。通过直方图对比分析可以看出，该算法的直方图分布均匀，高频突出，同时增强后图像的直方图更接近于原始图像，很好地突出了主要细节，抑制了非重要细节。

为了进一步说明本文算法的优点，对于图4中的4组实验，对各种算法增强后的局部区域进行了比较，如图6所示。从图6中可明显看出，本文算法的图像增强效果最好，在实现图像增强的同时更好地体现了图像的轮廓信息，并且与原始图像整体特性更加一致，很大程度上提高了增强后图像的可用性。

Figure 6 Detail comparison图6 细节对比图

Figure 7 Image enhancement comparison among the second group of different algorithms图7 第2组不同算法图像增强对比图

第2组实验分别用基于高斯滤波、双边滤波、L0范数的Retinex算法提取原始图像的高频信息，并与原始图像进行融合，比较结果如图7所示，图8为图7所对应的直方图。

Figure 8 Histogram of the corresponding image in Figure 7图8 图7对应图像的直方图

直观地比较增强后的图像很难看出差异，但是通过以上直方图对比分析可以看出，本文算法增强后的图像直方图分布更加均匀，保持了整体亮度值的一致，对比度明显，可以更好地突出主要细节。

4.2 增强效果客观评价

本文采用图像对比度、信噪比和信息熵来客观评价图像增强后的质量[29]。

图像的对比度公式为：

(14)

其中，Ii′,j′为图像像素的灰度值，k为图像局部块内像素数,k定义图像块的大小(2*k+1)。图像中所有局部块对比度的平均值即是图像的对比度。

图像的信噪比公式为：

(15)

其中，Gi为目标图像的最大灰度值，Gb为图像背景的灰度均值，σ′为图像背景像素灰度值的标准差。

图像的信息熵公式为：

(16)

其中,p(g)为灰度级g的概率密度，T为最大的灰度级,i″表示像素的灰度级。

本文分别计算了第1组和第2组不同算法的对比度、信噪比和信息熵，结果如表1和表2所示。

Table 1 Objective evaluation of image qualities obtained by the first group of different algorithms

由表1可以看出，Retinex算法和基于双边滤波的Retinex算法有较高的对比度值，但二者都导致了图像失真。主要原因是利用式(14)计算对比度度量时，图像块中存在的噪声点使得对比度的值很高，而信噪比和信息熵综合分析效果没有达到最优。本文算法可提高图像的对比度，同时信噪比和信息熵也取得了较好的结果。

通过表2可知，通过高斯滤波、双边滤波与Retinex算法结合提取高频信息并和原始图像融合也可提高原始图像的对比度、信噪比和信息熵。但是，Retinex算法提取轮廓再融合原始图像算法与双边滤波Retinex算法提取轮廓再融合原始图像算法在叠加原始图像前已经产生很多噪声，所以对比度值很高，其信噪比和信息熵提升整体而言没有达到最优；而本文算法的对比度、信噪比、信息熵综合分析效果最优，本文算法在图像增强后的视觉效果也是最好的。

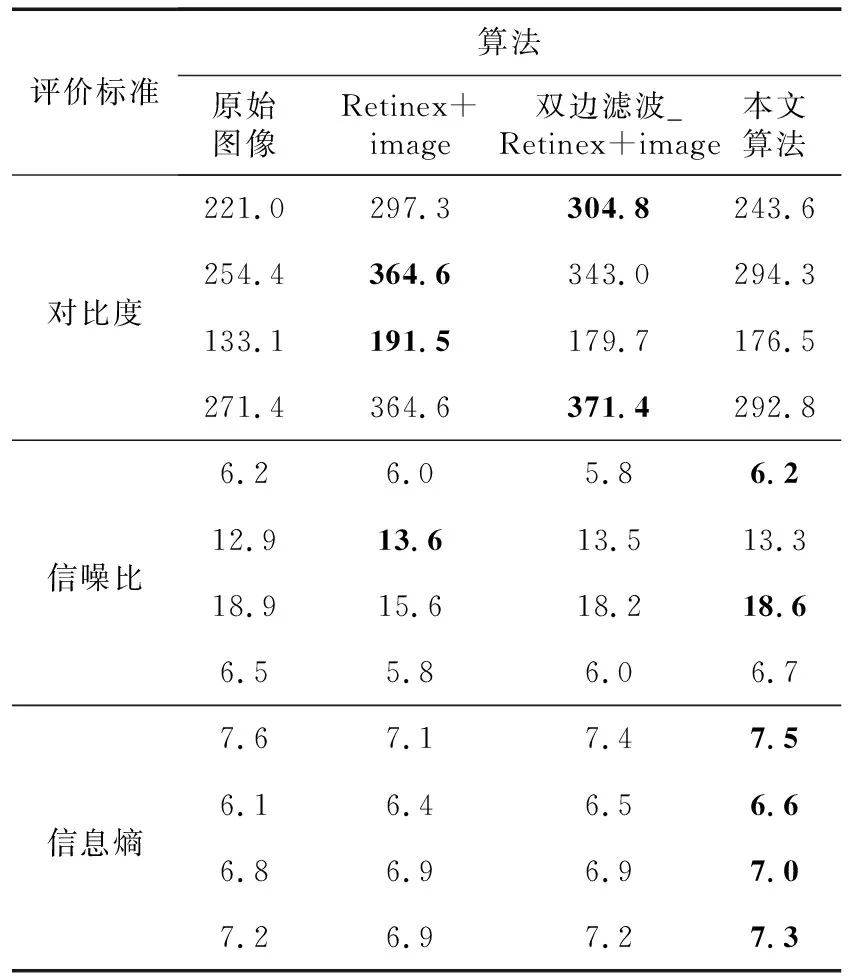
Table 2 Objective evaluation of image qualitiesobtained by the second group of different algorithms

5 结束语

本文通过研究传统的Retinex算法在图像处理中的不足之处，结合L0范数的图像平滑算子，提出一种在增强图像的同时又能很好地保持图像轮

廓信息的新算法RIEALN，并将传统的Retinex算法、基于双边滤波的Retinex算法与本文算法进行了对比分析，从主观和客观两方面进行了评价。本文所研究的图像增强算法无论对于Retinex领域还是L0范数领域而言，都是一个新的突破和创新。实验结果表明，本文算法可在增强图像对比度的同时更好地保留图像的边缘信息，更接近于原始图像。