带时间约束的Louvain算法在动态脑功能网络模块化中的应用研究*

淡杨超，王 彬,2，薛 洁，盛景业，刘 畅，詹威威

(1.昆明理工大学信息工程与自动化学院，云南 昆明 650500；2.昆明理工大学云南省人工智能重点实验室，云南 昆明 650500；3.云南省公安厅禁毒局，云南昆明 650228;4.提升政府治理能力大数据应用技术国家工程实验室,贵州 贵阳 550022;5.中电科大数据研究院有限公司总体技术研究中心,贵州 贵阳 550022)

1 引言

功能性磁共振成像技术fMRI(functional Magnetic Resonance Imaging)是目前一种常用的医学成像技术[1]，其原理是利用磁振造影测量神经元活动引发的血氧水平变化BOLD(Blood Oxygenation Level Dependent)信号对大脑活动进行检测，由于其非侵入性和无辐射暴露等优点而在医学方面得到了广泛应用。目前，fMRI主要分为任务态ts-fMRI(task state fMRI)和静息态rs-fMRI(resting state fMRI)[2]，由于rs-fMRI技术能够反映大脑固有的自发活动规律和连接模式，并且实验便于实施，受实验方案的干扰小，因此很多研究者采用rs-fMRI技术进行动态脑功能网络的重构[3]。目前大多数研究者基于rs-fMRI的脑网络研究都假定大脑的状态在数据采集时段内不随时间发生改变，但是随着研究的深入，很多实验结果显示，随着时间的变化，大脑各部分的BOLD信号会随着时间的变化而发生强弱变化，反映出大脑的状态是随时间改变的[4]。

基于rs-fMRI信号构建的功能连接(Functional Connection)网络研究发现，脑功能连接网络在时间序列上是高度可变的[5]，且在静息态会表现出自发的动态变化[6]，而且对于不同的任务，脑功能网络会表现出不同的特征[7]。由于静态脑网络难以展现出大脑的一些动态任务特征，因此很多研究者对大脑网络的多层表征形式进行了探究[8,9]，针对动态脑功能网络，Shine等人[10]利用rs-fMRI信号分析了帕金森病(Parkinson's disease)与大脑多巴胺分泌的相关性。Rukat等人[11]利用脑电数据构建隐马尔科夫模型，分析大脑的状态在时间和空间上的动态变化。Tian等人[12]统计了不同年龄的人其大脑的功能连接处于不同状态的持续时间长短，研究年龄与大脑反应时间的关系，此外还探究了功能连接的状态波动幅值变化与年龄的关系。当前动态脑功能网络已经成为了脑科学研究的主流方向，对动态脑功能网络的网络特征进行分析有助于了解大脑疾病的诱因，加强对某些心理疾病的辅助诊断，揭示大脑生理活动的运行机理。

上述研究致力于探究动态脑功能网络的网络特征在时间和空间的变化规律，从而发现动态脑功能网络的网络特征与大脑疾病之间的相关性。根据已有研究[13]发现，静态脑功能网络的模块化程度与大脑的认知功能存在强相关性，在需要不同认知功能的任务下大脑的模块化程度会发生改变。由于动态脑网络的模块化程度也会随着时间的变化而发生变化，因此很多研究者对动态脑功能网络的模块化现象展开了分析和研究，Mucha等人[14]对动态脑功能网络进行模块化探究，引入了一个多时间点耦合参数，以连接多个时间点，从而将相应的节点跨时间连接，得到一个新的质量评估函数来对网络进行模块化划分。Damicelli等人[15]通过构建脑网络的拓扑增强模型来减小脑网络模块化划分与真实脑网络拓扑结构之间的差距；Khambhati等人[16]研究了动态脑功能网络在任务态和静息态下模块化程度的变化，发现在不同任务下脑网络模块化程度有明显差别；Baniqued等人[17]的研究揭示了动态脑功能网络模块化程度与个人的学习记忆能力呈正相关关系；Siegel等人[18]研究了中风后恢复过程中动态脑功能网络的全局效率变化，并发现在中风恢复过程中动态脑功能网络模块化程度与语言恢复程度密切相关;Han等人[19]对颅脑损伤后恢复过程中动态脑功能网络模块化变化进行了研究，发现在恢复过程中脑网络模块性降低，参与系数变大，可根据动态脑功能网络模块化程度评估颅脑损伤恢复程度；Hilger等人[20]发现多动症与动态脑功能网络模块间和模块内的连接比率存在一定关联，并据此建立了多动症的动态脑功能网络模型，用以对婴幼儿多动症进行诊断，并使用了Louvain算法[21]对多动症患者动态脑功能网络进行模块划分。

Louvain算法的核心思想是以达到模块度的最大值为指标来划分模块，而模块度最大化面临的一个问题是在某些情况下，可能会检测不到低于一定规模的小模块，这个问题在小规模网络的模块化研究中尤为突出[22]。由于基于rs-fMRI重构的动态脑功能网络一般是90个节点[23]，属于小规模网络，因此模块化分辨率对实验结果的影响也更加明显。针对Louvain算法无法正确识别动态脑功能网络中小规模模块的问题，本文提出了一种带时间约束的Louvain算法来提高模块的分辨率并应用该算法对动态脑功能网络进行模块分析。

Figure 1 Processing of dynamic brain function network construction and module division图1 动态脑功能网络构建及模块划分流程

2 带时间约束的Louvain算法动态脑功能网络模块化分析

2.1 动态脑功能网络构建及模块化流程

本文利用AAL(Anatomical Automatic Labeling)模板[23]将大脑分为90个脑区，采用大小为W，步长为L的滑动窗口技术对rs-fMRI数据进行动态特征观测窗口的重建，计算每个窗口内90个脑区中每2个脑区之间的皮尔逊相关系数(Pearson Correlation Coefficient)[24]，并将脑区间的皮尔逊相关系数作为脑区间的连接强度，构建动态脑功能网络。图1所示为动态脑功能网络构建流程。

模块性是复杂网络系统的基本特征，网络模块是指一组连接紧密的节点，通常每一个模块是专门处理信息的基础单元。功能神经影像研究表明，人类大脑在大尺度的功能网络上具有很好的模块化结构。一般用模块度(Modularity)[25]Q表示模块的划分程度，Q值的取值为[-0.5,1)[25]，模块度Q值越大，模块划分得到的单一模块规模越大，网络总的模块数量越少。当Q值在0.3～0.7时，网络模块的划分最好[26,27]。

Louvain算法[21]是一种基于多层次优化模块度的算法，它能够发现层次性的模块，并且模块辨识准确性高、计算复杂度低、效率高，因此被广泛应用于模块化研究。

图2所示的是使用Louvain算法对动态脑功能网络进行模块划分得出的不同时间点的模块度Q值时间序列，其中，图2a和图2c为2个健康人样本，图2b为自闭症患者样本。由图2可以看出，3个样本的峰值分别达到0.82，0.83，081，最小值分别为0.71，0.68，0.55，平均值分别为0.77，0.76,0.71，而模块度Q值的合理范围应该在0.3～0.7。规模过大的脑功能模块可能会使得一些重要的亚功能脑模块被忽略，不利于深入研究脑功能网络的属性。

Figure 2 Dynamic brain function network modularity (Q) sequence by Louvain algorithm图2 动态脑功能网络Louvain算法模块化Q值序列

针对上述问题，本文提出了一种带时间约束的Louvain算法，其原理如图3所示，图3a中原Louvain算法要不断迭代至模块度增益为0时才停止，而带时间约束的Louvain算法，如图3b所示，在不断合并小模块过程中，采用与时间相关的约束使得迭代在适当的时候停止，因此动态脑功能网络中的一些小规模模块也会被识别出来。

Figure 3 Comparison of Louvain algorithm and time-constrainted Louvain algorithm图3 原Louvain算法和带时间约束的Louvain算法划分结果对比图

2.2 带时间约束的Louvain算法原理与步骤

2.2.1 带时间约束的Louvain算法

首先，针对动态脑功能网络给出如下定义：

定义1根据Louvain算法，定义动态脑功能网络中模块化划分优劣的判定标准，即模块度Q为：

(1)

(2)

其中，Ai,j表示脑区i和脑区j之间的连接强度之和;m表示整个动态脑功能网络中所有脑区的连接强度之和;ki=∑jAi,j是连接到i脑区的所有连接的连接强度之和;δ(ci,cj)是一个二值函数，当脑区i和脑区j被划分到同一个模块时,其值取1，当脑区i和脑区j不属于同一个模块时，其值为0。

定义2改进的模块度增益ΔQ：

(3)

其中，ΔQ即为带时间约束的Louvain算法中的模块度增益，用来决定动态脑功能网络中脑区模块合并的方向；∑in表示被划分到模块C内的所有脑区之间的连接强度之和；∑tot表示模块C内所有脑区与模块C外的所有脑区之间的连接强度之和；ki表示脑区i与其他所有脑区之间的连接强度之和;ki,in表示脑区i和模块C内所有脑区的连接强度之和;m表示动态脑功能网络中所有脑区的连接强度之和。

定义3改进的迭代终止系数η：

(4)

由于原Louvain算法是基于贪婪思想的算法，向着模块度Q值最大方向合并，在合并过程中会以损失一些小规模的模块为代价，而动态脑功能网络是与时间密切相关的，因此本文给出了一个迭代终止系数η。该系数综合考量了所有时间点上Q值的平均分布情况，当ΔQ=η时，终止迭代，并将此时的模块划分作为最终的模块划分。其中，Qmax_i为原Louvain算法计算出的n个时间点上除时间点i外所有时间点最大Q值，Qmin_i为原Louvain算法计算出的n个时间点上除时间点i外所有时间点最小Q值。

2.2.2 动态脑功能网络模块化实现步骤

步骤1将网络中每一个节点视为一个独立的模块，合并相邻的模块并计算合并后的模块度增益ΔQ，对网络中所有节点都进行邻居节点合并，直到模块度增益ΔQ≤η为止；

步骤2将2个合并后的模块视为新模块，合并新模块和其邻居模块并计算模块度增益ΔQ，对网络中所有新模块都进行邻居模块合并，直到模块度增益ΔQ≤η为止；

步骤3重复步骤2，直至整个网络的模块度增益ΔQ不大于迭代终止系数η，此时所得出的模块结构即为带时间约束的Louvain算法最终所求的模块划分。算法流程如图4所示。

Figure 4 Flow chart of time-constrainted Louvain algorithm图4 带时间约束的Louvain算法流程图

3 实验与结果分析

3.1 数据来源和预处理

本文实验的数据来源于公开脑网络数据库INDI(International Neuroimaging Data-Sharing Initiative)中的斯坦福大学(Stanford University)采集的40组脑网络数据样本组成的样本集S[28]。40个样本年龄在7.5～12.9岁，其中20个自闭症患者(ASD组)，样本年龄在7.5～12.9岁，20个健康人(TC组)，年龄在7.8～12.4岁。重复时间TR(Repetition Time)为2 s，回波时间TE(Time of Echo)为30 ms，采集矩阵为64*64，视野FOV(Field Of View)为20 cm*20 cm，翻转角Flip Angle为80°，共采集180个时间点数据。

首先对由rs-fMRI采集得到的原始数据进行预处理，具体过程包括去除不稳定时间点；时间层校正；头动校正；颅骨去除；空间标准化；带通滤波等，根据AAL模板将全脑共划分成90个脑区，提取得到90个脑区的BOLD信号时间序列。数据预处理采用的平台工具是duke brain imaging analysis center的Resting State Pipeline[29]。

3.2 动态脑功能网络的构建

本文实验数据共采集了180个时间点，去除前4个不稳定时间点，利用滑动窗口技术对BOLD-fMRI信号进行窗口观测，取滑动窗口长度为W=40，滑动窗口步长L=1，得到包含137个时间点的脑网络观测数据。在每一个时间点上计算两两脑区之间的BOLD信号的皮尔逊相关系数，将脑区间的皮尔逊相关系数作为脑区之间的连接强度系数，可以得到每一个时间点上的90*90的脑网络相关系数矩阵。其中，皮尔逊相关系数取值为-1～1，本文将脑网络相关系数矩阵取绝对值表示其相关程度，绝对值越大相关程度越高，并去除自连接，将对角线元素置0。

此外，由于本文的实验组是ASD组和TC组各20个样本，为了提取出ASD组和TC组各自的特征，对ASD组和TC组样本分别进行了组平均的统计。具体地，将ASD组20个样本数据中相同时间点的脑网络相关系数矩阵取平均得到组平均数据，TC组同上，最终将得到的ASD组和TC组 的组平均数据进行阈值化处理[30]。根据已有研究[31]，脑网络相关系数矩阵的阈值选取在0.45以上时脑网络具有小世界性和完整性。本文选取阈值为0.5将脑网络相关系数矩阵进行阈值化，整个数据预处理流程如图5所示。

Figure 5 Experimental principle and process图5 实验原理及流程

3.3 带时间约束的Louvain算法的动态脑功能网络模块化实验及结果分析

按照2.2.2节中带时间约束的Louvain算法对经过数据预处理的动态脑功能网络进行模块划分，并分别对不同实验的步骤和实验结果进行分析。

3.3.1 模块度Q值分布对比实验及结果分析

AD9833芯片可通过VOUT引脚提供各种输出，可完成方波输出、正弦波输出和三角波的输出。控制寄存器的 OPBITEN（D5）和 Mode（D1）bits决定着AD9833芯片输出波形的类型。其控制逻辑如表2所示。

首先，对预处理数据分别使用原Louvain算法和带时间约束的Louvain算法进行模块划分，并计算每一个时间点的模块度，2种算法的动态脑功能网络模块化Q值如图6所示。

Figure 6 Comparison of modularity (Q) between Louvain algorithm and time-constrainted Louvain algorithm图6 原Louvain算法和带时间约束的Louvain算法Q值对比图

图6a、图6b、图6c所示为3个样本分别使用2种算法进行模块划分后的结果，图6中T1为使用原Louvain算法对动态脑功能网络进行模块划分得到的模块度Q值，T2为使用带时间约束的Louvain算法得到的动态脑功能网络模块度Q值。由图6可以看出，原Louvain算法对动态脑功能网络进行划分后得到的模块度正常值分布上限均超过了0.7，并且有较多的异常数据点，而带时间约束的Louvain算法其模块度值分布位于0.35～0.56，其Q值均处在合理范围之内，表明带时间约束的Louvain算法能够对动态脑功能网络进行更好的模块划分。2种算法的Q值具体统计如表1所示。

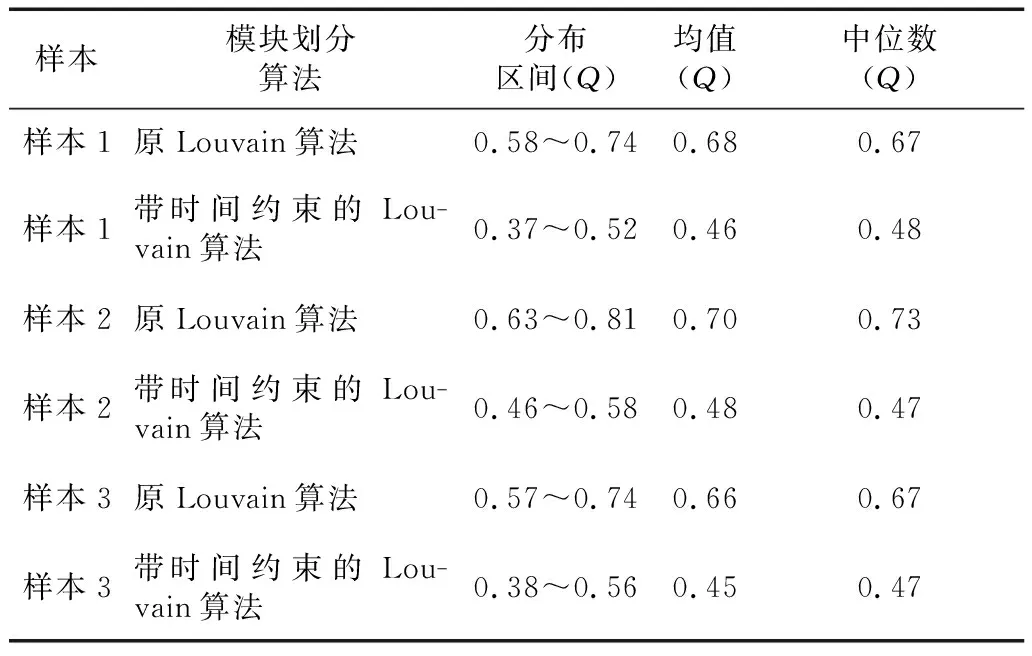
Table 1 Comparison of modularity (Q) between Louvainalgorithm and time-constrainted Louvain algorithm

3.3.2 模块划分对比实验及结果分析

统计发现，基于带时间约束的Louvain算法得到的动态脑功能网络模块划分将90个脑区分成了6或7个不等的模块。本文对ASD组和TC组分别进行500次实验，滑动窗口选取W=40，计算137个时间点的模块划分，对每一次实验统计模块划分数量和每一个模块内含脑区数量。结果显示，模块划分为6个模块的次数占总实验的4.2%，模块划分为7个模块的次数占总实验的95.6%，模块划分为5个模块的占总实验次数的0.2%；而使用原Louvain算法对动态脑功能网络进行模块划分，得到4～5个不等的模块，其中，模块划分数量为4的次数占总实验次数的42.6%，模块划分数量为5的次数占总实验次数的57.4%，部分实验结果如表2、图7和图8所示。

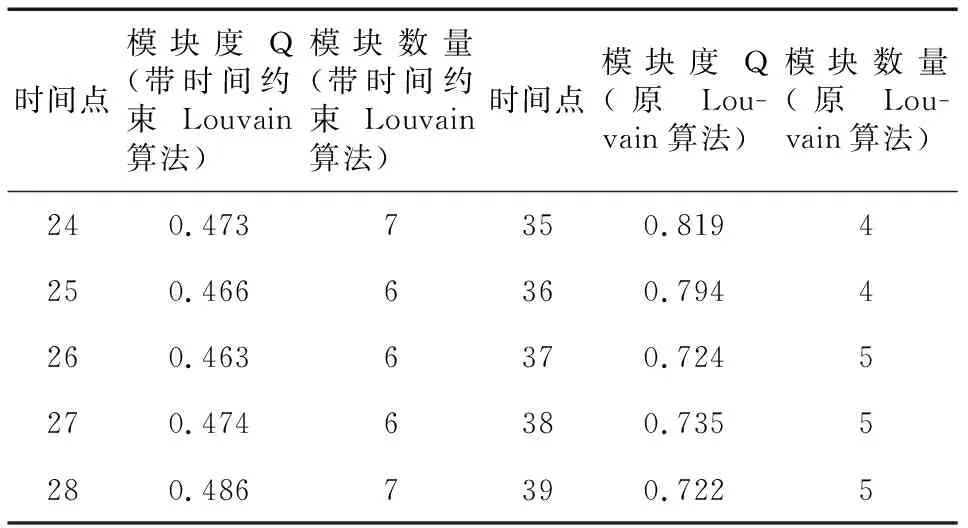
Table 2 Partial time point modularity and moduledivision number of time constrainted

图7所示为原Louvain算法部分时间点的模块划分频次统计图，图7中，纵坐标为脑区数量，横坐标为动态脑功能网络划分模块编号，图中最小模块包含13个脑区，最大模块包含34个脑区;图8所示为带时间约束的Louvain算法部分时间点模块划分频次图，图8中，最小模块包含4个脑区，最大模块包含23个脑区。从图8中可以看出，带时间约束的Louvain算法没有高于30个脑区的模块，而且有只包含几个脑区的小模块，因此与原Louvain算法相比，本文算法可以识别出小规模的模块，对脑网路的模块划分具有合理性和有效性。

Figure 7 Brain region quantity statistics of each module at partial time points by Louvain algorithm图7 原Louvain算法部分时间点各模块包含脑区数量统计图

Figure 8 Brain region quatity statistics of each module at partial time points by time-constrained Louvain algorithm图8 带时间约束的Louvain算法部分时间点各模块包含脑区数量统计图

3.3.3 TC组和ASD组的模块化对比实验及结果分析

带时间约束的Louvain算法对预处理数据进行模块划分，对于每一个样本，得到一组时间序列上的Q值，将患有自闭症(ASD)患者的Q值和对照组(TC)的Q值进行对比，其具体分布如图9所示。

Figure 9 Compassion of modularity(Q) between TC&ASD图9 TC&ASD组Q值对比

图9a中，箱型图x轴为健康人(TC)组和自闭症(ASD)患者组，y轴为Q值。由图9a中可以看出，ASD组的Q值整体上小于TC组的，而且，ASD组有很多时间点的Q值异常低，由此可以看出，TC组相比较于ASD组，有明显的模块化属性，而ASD组出现了Q值降低，这显示出由于疾病对动态脑功能网络的影响，病人的动态脑功能网络模块属性受到了破坏，因此ASD组的功能模块性能有所降低。图9b为ASD组和TC组的Q值分布图，图中TC组的Q值分布相较于ASD组更加集中，说明TC组的动态脑功能网络模块化程度变化相较于ASD组更小，TC组的动态脑功能网络与ASD组相比具有更好的稳定性。图9c中，x轴为时间点，y轴为Q值，图9c中可以看出，在合理的Q值范围内，ASD组的Q值时间序列普遍低于TC组。表3为上述2个样本的Q值序列统计。

Table 3 Statistics of modularity(Q) between TC&ASD

另外，本文还使用spss软件对实验结果进行了样本分析，如表4所示，首先对2组Q值序列进行莱文方差等同性检验，得到P=0.199，2组数据为等方差，再对2组数据进行独立样本t检验，得到P<<0.05，说明ASD组和TC组的Q值序列具有统计学意义上的差别，具体来说，自闭症(ASD)患者组的模块度Q值远低于健康人(TC)组，而模块度Q值大小表明了动态脑功能网络的模块性高低，自闭症患者会表现出语言交流障碍和智能障碍，其大脑功能相较于正常人有一定的缺失。本实验得出自闭症患者动态脑功能网络模块性低于健康人，与自闭症对大脑的影响相符，因此可以使用动态脑功能网络的模块化特征对自闭症致病原理以及其病理特征进行探究，从而为自闭症的诊断提供一定的依据。其t检验结果如表4所示。

3.3.4 原Louvain算法和改进的Louvain算法效率对比

对同一组数据分别使用原Louvain算法和带时间约束的Louvain算法进行模块划分，统计其所需要时间。本次实验平台为：处理器Intel i5-4200H 2.8 GHz，内存4 GB，显卡NIVDIA GTX860M。

对同一样本分别采用2个不同的算法进行模块划分，并计算每一次实验所需要的运行时间。由于带时间约束的Louvain算法设置了迭代终止系数η，其迭代次数会小于原Louvain算法，因此带时间约束的Louvain算法运行时间少于原Louvain算法的，计算的效率也要高于原Louvain算法的。对3个样本分别使用2种算法进行模块划分，原Louvain算法平均计算时间为0.131 s，带时间约束的Louvain算法平均计算时间为0.066 s，带时间约束的Louvain算法相较于原Louvain算法效率提高了49.6%。

综上所有实验结果所述，对本文提出的算法和原Louvain算法在动态脑功能网络模块化过程中的实验效果分析如下：

(1)从算法的原理上看，Louvain算法是以模块度增益最大为目标来进行模块划分，且原Louvain算法针对的是大规模网络(数百万节点)，而动态脑功能网络从规模上说属于小规模网络(数百个节点)，因此若用原Louvain算法对动态脑功能网络进行模块划分将导致严重的偏差，影响模块化效果；本文提出了基于时间序列的迭代终止系数，通过提前终止模块合并得到具有更好效果的动态脑功能网络模块划分，得到更加合理的动态脑功能网络模块度Q值。

Table 4 Independent t test between TC&ASD

(2)从样本的模块划分来看，原Louvain算法进行模块划分得到的模块数量少于本文算法的且其模块数量不稳定，具有很大的随机性，而本文算法在多次模块划分实验中得到的模块划分数量基本不变，具有较好的实验稳定性。此外，原Louvain算法得到的模块包含大量脑区，缺乏对小模块的识别能力，而本文算法能够准确识别出小模块。

(3)从对不同类的样本识别上看，本文所提出的带时间约束的Louvain算法得到的动态脑功能网络模块划分在自闭症患者和健康人2类样本上能够有特别明显的区别，自闭症患者由于疾病影响导致其动态脑功能网络的模块性降低，二者的实验结果满足统计意义上的区别。

(4)从计算的效率上看，相较于原Louvain算法，本文提出的带时间约束的Louvain算法具有更高的计算效率，其平均运行时间也小于原Louvain算法的，在针对大量样本的计算上能够节省大量的时间和计算资源。

4 结束语

由于原Louvain算法过分追求模块度Q值最大化而忽略了对一些小规模模块的辨识，因此在使用Louvain算法进行动态脑功能网络模块划分时，不能够准确辨识动态脑功能网络。针对这一问题，本文提出了带时间约束的Louvain算法，考虑到动态脑功能网络的构建是与时间密切相关的，并且其模块化属性也会随着时间的不同而发生变化，因此本文给出了一个基于时间约束的迭代终止系数。该系数综合考量了所有时间点上Q值的平均分布状况，并设定寻找最佳模块划分结果的过程中，当满足该系数要求时就终止迭代，从而在避免Q值过大的同时保证模块划分结果的合理性。

使用该算法对健康人和自闭症患者的动态脑功能网络进行了模块化分析，分别进行了3个对比实验并进行了分析。使用原Louvain算法和本文算法进行动态脑功能网络模块划分，原Louvain算法得到的模块度Q值基本超出了正常范围，而经过改进后的算法得到的模块度Q值均处于合理范围之内。此外，通过多次实验结果可知，原算法得到的模块划分存在随机性，实验结果差异很大，模块数量少且其单一模块包含脑区数量过多，无法识别出小规模的动态脑功能网络模块；而本文算法得到的模块划分较原算法有更高的稳定性和更小的模块规模，能够识别动态脑功能网络中的小规模模块。最后，通过对自闭症患者样本和健康人样本的对照实验，发现自闭症患者(ASD)动态脑功能网络模块化程度比健康人(TC)的动态脑功能网络有所下降，且二者具有统计学意义上的区别。

本文提出的带时间约束的Louvain算法对动态脑功能网络的模块化过程中存在的Q值高于合理范围并且对动态脑功能网络小规模模块辨识度不高的问题提出了一种解决方案，为自闭症的动态脑功能网络属性研究及自闭症的辅助诊断提供了一种辅助方法，同时也对其它同类动态网络模块属性的研究具有一定的参考价值。