NOMA双连接异构网络条件解耦设计架构及性能分析*
2020-07-27纪澎善贾向东徐文娟
纪澎善,贾向东,2,路 艺,徐文娟
(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070;2.南京邮电大学江苏省无线通信重点实验室,江苏 南京 210003)
1 引言
5G异构网络HetNets(Heterogeneous Networks)被认为是达到千倍数据速率目标的有效方法。在HetNets中,配备低功率基站BS(Base Station)的小小区可以与宏小区结合使用,形成多层HetNets,与当前的4G网络相比,将提供更高的容量,同时所提供的移动数据流量大幅增加[1]。然而,在未来的HetNets中,由于密集部署的低功率短距离BS,用户设备UE(User Equipment)与BS的数量将相差无几,同时小区的部署也更加不规则。这种情况下,在HetNets中会产生一些不可忽视的问题,例如UE级联及其标准[2,3]。因此,一些早期的工作集中在用户级联的解决方案和提出有效的用户级联准则上,如最大平均接收信号功率和信号干扰噪声比SINR(Signal-to-Interference-Noise Ratio)[4 - 6]。
从UE的角度来看,具有最大下行链路DL(DownLink)接收信号功率的BS(或接入点)不一定是具有最大上行链路UL(UpLink)功率的BS。此外,由于移动UE的功率限制,UL容量受到限制。因此,文献[7]引入了解耦上行链路和下行链路级联DUDA(Decoupled Uplink and Downlink Association)的概念,其中移动UE可以在DL和UL传输方向上分别连接至不同的BS。由于UL和DL级联相互独立,因此DUDA中的可行级联比耦合UL和DL级联CUDA(Coupled Uplink and Downlink Association)更灵活,从而可以改善UL容量,同时可以减少来自UL的UE干扰并且克服移动UE的功率约束。Boccardi等[8]确定并解释了DUDA设计的论点,并提出了从4G LTE / LTE-A到5G实现DUDA设计的可行方案。文献[9]则侧重于两层HetNets的研究。近期关于DUDA设计的最新研究还专注于其在5G网络中的实现。文献[10]对全双工HetNets中的DUDA进行了设计,并研究了密集回程连接对DUDA性能的影响。
为了进一步改善频谱效率SE(Spectrum Efficiency),3GPP在版本12中引入了HetNets中的双连接DC(Dual-Connectivity)概念[11]。在DC模式的HetNets中,允许每个UE同时与UL和DL中的2个不同接入点通信。结果发现,当DC与某些先进技术相结合时,可以实现更好的SE增益,如非正交多址接入NOMA(Non-Orthogonal Multiple Access)和毫米波技术[12 - 14]。文献[15,16]则侧重于DC模式的HetNets中的DUDA设计,并研究了联合应用DUDA和DC的2层HetNets。结果表明,相比传统的单连接,DC能够更灵活地实现UE级联。
基于上述分析,本文采用DUDA来增强UL传输容量,从而提高整个网络的吞吐量。但是,仍然存在以下问题:首先,现有的工作主要集中在单连接模式的双层HetNets上。在采用DC模式的HetNets中研究DUDA设计的工作非常少[15,16],且这些研究仅考虑了简化的双层HetNets。众所周知,在多层HetNets中,特别是在DC模式的HetNets中,DUDA的设计比在双层HetNets中更加灵活和复杂。原因在于,随着层数的增加,可能的DUDA方案的数量呈指数增长,这使得早期工作中提出的用绝对级联概率来评估网络性能变得困难且复杂。目前,这种多层HetNets的性能尚不清楚。此外,对于不同的DL级联,相应的解耦UL性能是不同的。因此,找到一种有效的框架非常重要,利用该框架可以从所有候选的DL级联中选择可行的DL级联方案,使得解耦UL级联的平均性能最佳。在实践中,解决上述问题的有效方法是基于DL级联对所有可能的解耦级联进行分类,在可行的DL级联条件下设计解耦UL级联。同时,还可以推导出在给定DL级联约束条件下的相应的条件级联概率。显然,利用这种条件级联框架可以更清晰地研究多层HetNets,克服了多层HetNets的复杂性这一问题。其次,由于双层HetNets的限制,在现有文献中,DC模式HetNets的DUDA设计均在同一层中进行。也就是说,这些工作仅研究了非跨层DC模式。但是,通常在同一层内的BS具有相同的服务级别,实际的DC模式HetNets关注于不同的级联链路上需要不同服务级别的场景,即跨层级联。例如,宏层提供控制信令,而其他层提供数据的情况。
最后,当DC正交使用可用频谱时[15,16],由于采用传统的正交多址接入OMA(Orthogonal Multiple Access),系统的频谱效率较低。使用NOMA技术可以克服这个问题,NOMA技术是5G的另一个关键技术,其在发射机处使用叠加编码SC(Superposition Coding)并在接收机处利用连续干扰消除SIC(Successive Interference Cancellation)[17 - 19]。在发射机处,基于不同功率电平叠加和发送到不同UE的信号。在接收器处,基于接收器信号强度,UE在解码其自己的信号之前使用SIC技术来移除针对其他UE的信号,由于通过共享相同的资源块来传递更多信息,NOMA方法的实现改善了系统频谱效率SE。
2 系统模型与问题描述
2.1 系统模型及信道假设
考虑如图1所示的由宏小区层M层(Microcell tier)、微微小区P层(Picocell tier)和毫微微小区F层(Femtocell tier)构成的3层异构网络,每一层具有不同的发射功率、覆盖范围和空间密度等。其中,高功率宏小区由低功率短距离的小BS所覆盖。通常情况下,同一层中的BS具有相同的发射功率。PM、PP、PF分别表示宏基站MBS(Microcell Base Station)、微微小区基站PBS(Picocell Base Station)和毫微微小区基站FBS(Femtocell Base Station)的发射功率,且遵循功率约束PM>PP>PF。将MBS、PBS和 FBS的位置建模为密度依次是λM、λP和λF的独立泊松点过程PPP(Poisson Point Process)ΦM、ΦP和ΦF。同时,将UE建模成密度为λU的独立PPPΦU,其发射功率为PU。整个网络假设为全负载,即λU>λi,i∈{M,P,F},且每层的每一个BS至少级联一个UE 。所有的网络元件配备单天线,且总可用信道带宽为B。
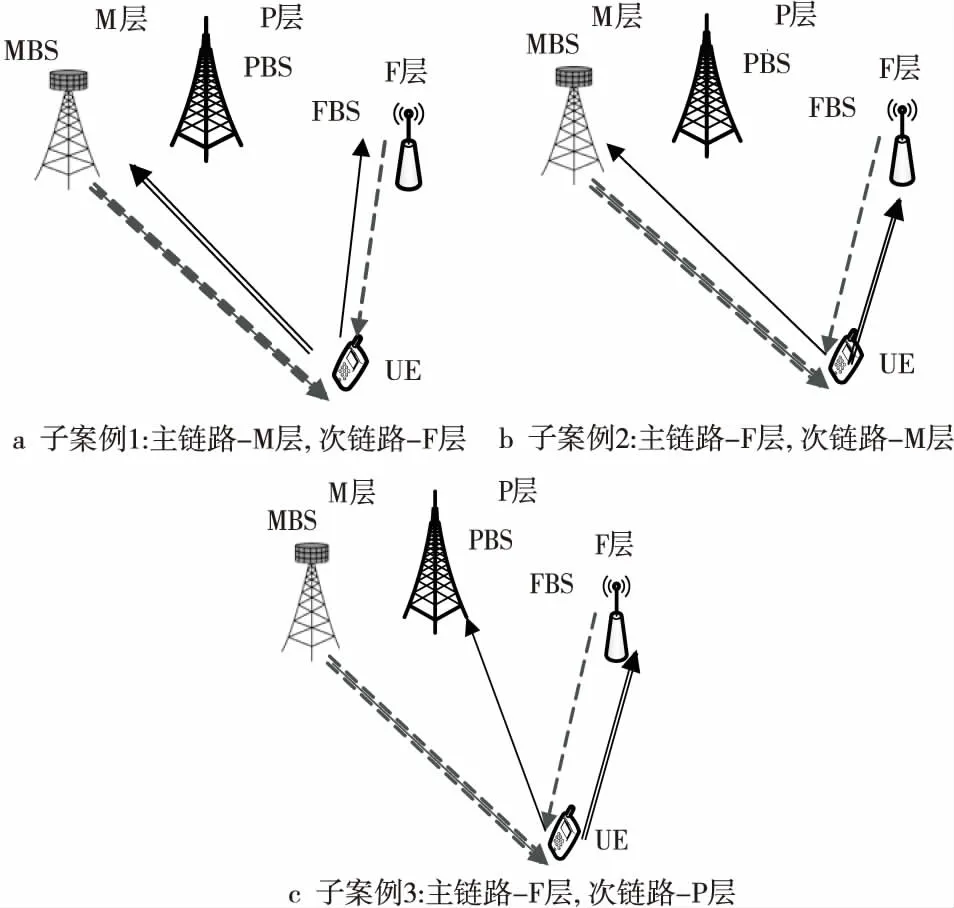
Figure 1 Decoupling UpLink associations under given DL connectivity condition图1 给定DL连接条件下的解耦UL级联

frOi(x)=2πλixe-πλix2,i∈{M,P,F}
(1)
2.2 DUDA和双连接
将DC用于DL和UL传输,即,给定UE在DL或UL中同时与2个不同的服务BS相级联。在DL中,使用传统的DL接收信号功率DRSP(Downlink Received Signal Power)准则,其中,主要DL接入层为提供最强DRSP至给定UE的最近BS,次要DL接入层为提供第2最强跨层DRSP至给定UE的最近BS。与DL级联不同,在DUDA方案中,UL接入利用最短距离准则,根据特定UE到最近BS所获得最大UL 接收功率进行级联。因此,UE首先选择主要UL接入层即与给定UE距离最近的BS以及次要UL接入层即与给定UE第2近距离的BS由式(2)和式(3)产生:
(2)
(3)
其中,Xk表示从特定UE到第k层的最近BS的欧几里德距离,Sec{·}表示二阶非最佳统计。由于使用不同的级联准则,在解耦DC方案中UL和DL的主次接入点不同。同时,由于考虑了跨层DC,所以DL或UL中的主次接入BS不在同一层中,且每个UE处主信号UL的功率分配因子是αP。
2.3 解耦上行链路级联
由于本文所考虑的是3层异构网络,所以存在很多解耦UL和DL级联。此处,考虑DL中给定UE的主要和次要DL分别级联至M层和F层最近的BS,即,M层是主要接入层,F层是次要接入层。解耦UL级联的条件是给定DL的 DC模式级联,由于功率约束,如图1所示有3种可能的UL级联情况。图1a为CUDA方案,图1b和图1c为DUDA 方案。
2.4 NOMA传输


(4)

(5)
对于信道质量较差的次要接收器,利用如式(6)所示的SINR将叠加的主信号作为噪声直接解码其所需信号[16 - 20]。
(6)

3 解耦上行链路条件级联概率

(7)
由于到一个PPP最近点的距离遵循瑞利分布,因此,可由式(1)得到引理1,其给出了所考虑场景的DL级联概率。
引理1对于给定的DL级联情况,其中主要和次要DL级联至M层和F层,基于DRSP标准,给定的DL级联概率表达式如式(8)所示:
(8)
3.1 主链路-M层,次链路-F层
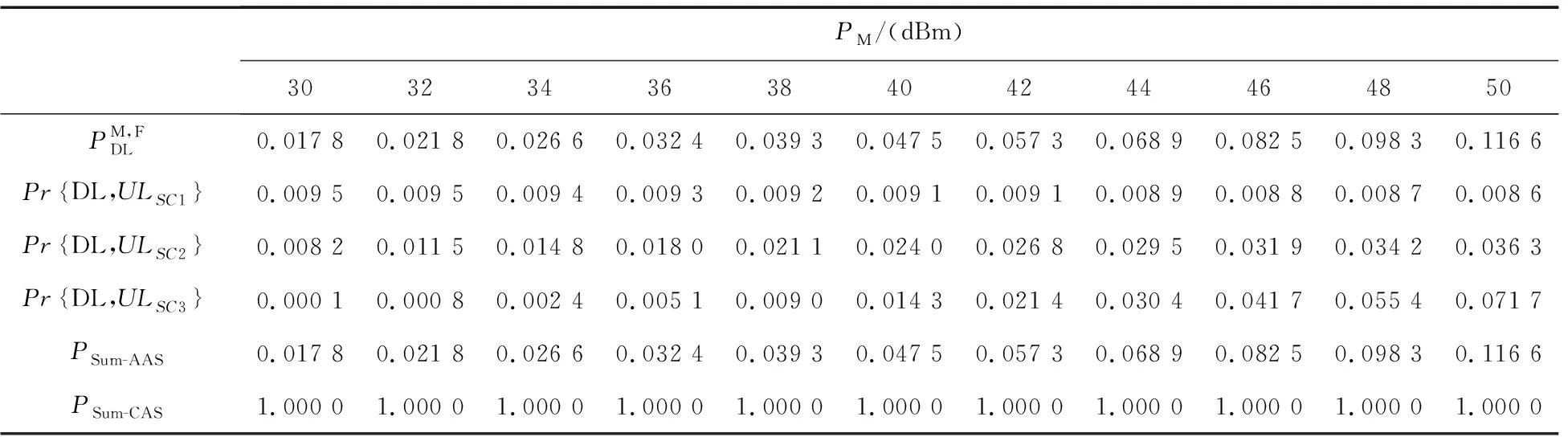
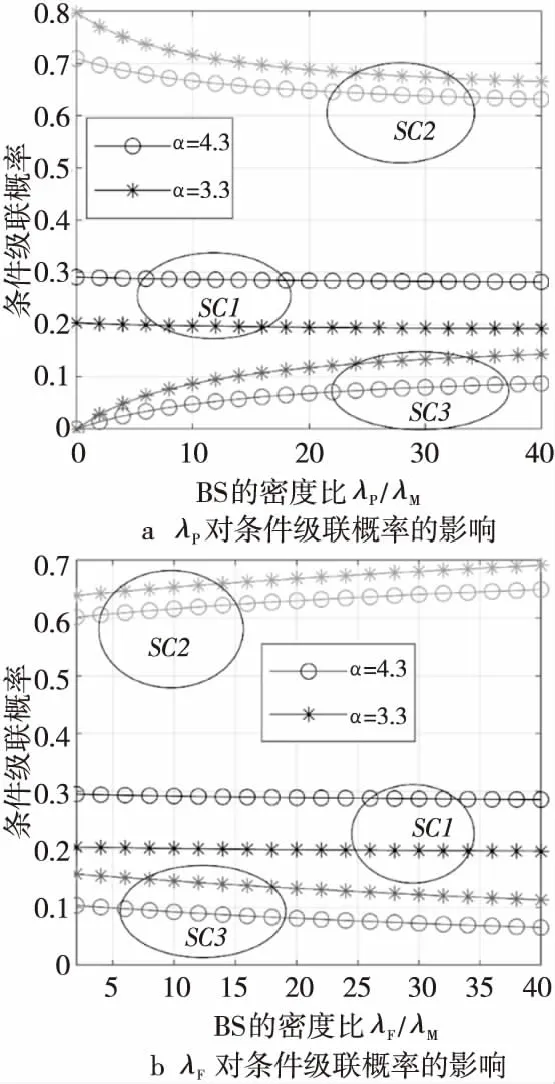
基于给定DL级联的级联概率,需推导出UL条件级联概率。子案例1是耦合的UL和DL级联,即主要和次要UL连接与其DL连接相同。从图1a可以看出,级联条件ULSC1:rOM PSC1=Pr{ULSC1|DLM,F}= (9) (10) 然后,结合式(9)和式(10)及引理1,得到命题1。 命题1对于给定的DL主要和次要连接,如图1a所示的子案例1为UL和DL主要和次要连接一致的耦合级联方案。子案例1的条件级联概率为: (11) 如图1b所示的子案例2(SC2)考虑了主要和次要DL连接的解耦UL级联。在这种情况下,距给定UE最近的为F层,其次为M层,距P层最远。因此,UE选择其主要UL连接到F层,其次要UL连接到P层。这种情况考虑了2个解耦级联,即解耦主要连接和次要连接。UL主要和次要级联具有与DL相反的顺序,可得到UL级联条件为ULSC2:rOF PSC2=Pr{ULSC2|DLM,F}= (12) 利用功率限制PM>PP>PF,得到式(12)最后一项分子的表达式为: (13) (14) (15) 合并式(12)~式(15)得到命题2。 命题2在如图1b所示的子案例2中,尽管UL与DL级联至相同层,但是主要和次要UL与级联顺序相反的DL完全解耦。子案例2对应的条件级联概率为: (16) 在如图1c所示的子案例3(SC3)中,给定UE距F层的BS最近。然而,不同于子案例2,在子案例3中,给定UE更接近于P层的BS而非M层。在该子案例中,主要和次要UL也是完全解耦的并且分别与F层和P层相级联。相应的UL级联条件是ULSC3:rOF (17) 由DL级联条件DLM,F和解耦的UL级联条件ULSC3,可得到Pr{DLM,F,ULSC3}表达式为: Pr{DLM,F,ULSC3}= (18) 因此,可得到命题3 命题3如图1c所示的子案例3考虑了一个完全解耦UL级联场景,其中主要和次要UL分别与F层和P层相级联。相关的条件级联概率为: (19) 本节重点介绍每个子案例中给定UE与其主要和次要接入点之间距离的统计描述。类似于条件级联概率,统计描述也经常在序列部分中用来开发系统性能。同时,在这项工作中,还考虑了基于传统DRSP的CUDA案例。除了DUDA案例的接入距离之外,在此3层HetNets中也对CUDA案例进行了分析。对于一个给定的DL级联,尽管对于所有子案例耦合UL接入点复杂度相同,但是不同级联子案例的统计描述不同。 (20) (21) (22) (23) (24) (25) 因此,经过数学推导,可得到引理3。 e-π(λP+λM)(PM/PF)2/αr2)-e-πλMr2(e-πλPr2- e-π(λP+λM)(PP/PF)2/αr2)} (26) e-π(λP+λF(PF/PP)2/α)(PP/PF)2/αr2)- e-πλFr2(e-πλPr2-e-πλP(PP/PF)2/αr2)]} (27) (28) (29) 此外,为了评估可实现的性能增益,研究了基于DRSP准则的耦合UL和DL方案的性能,其产生了次优的系统性能。为此,需要给定UE与M层最近的BS之间距离的统计描述。将次优UL接入距离的CDF表示为: r,DLM,F,ULSC3} (30) (e-π(λM(PM/PF)2/α+λP(PP/PF)2/α)r2- e-π(λM(PM/PF)2/α+λP(PM/PF)2/α)r2))] (31) e-π(λM+λF(PF/PM)2/α)r2-e-π(λM+λF(PF/PM)2/α)(PM/PP)2/αr2)- (e-π(λM+λF(PF/PP)2/α)r2-e-π(λM(PM/PP)2/α+λF(PF/PP)2/α)r2)] (32) (λP(e-π(λP+λF(PF/PP)2/α)(PP/PM)2/αr2-e-π(λP+λF(PF/PP)2/α)r2))/ (λP+λF(PF/PP)2/α)] (33) 本节根据覆盖概率CP(Coverage Probability)评估网络UL的性能。同时,除了基于DUDA的HetNets的性能外还得到了基于CUDA的HetNets性能。首先推导出主要和次要UL的SINR覆盖概率。其次,根据使用SIC的NOMA的思想,当以下条件成立时,主要信号将成功解码:(1)主接收器可以解码叠加的次要信号;(2)在执行SIC处理之后,主接收器可以解码其自己的目标信号。对于给定的级联子案例k,k∈{1,2,3},由式(4)和式(5)可得到基于DUDA主要UL的SINR覆盖概率为: (34) 其中,τP和τS分别为主要和次要UL基于目标速率的SINR阈值,上标D、C分别表示基于DUDA和CUDA,将式(4)和式(5)代入式(34)得: (35) 与主接收机不同,由于链路质量差,次要接收器通过将接收到的主信号视为噪声来解码其目标信号。因此,对于给定的级联子案例k,利用式(36)可得到次要UL的SINR覆盖概率为: (36) 命题4虽然在NOMA方案中实现了解耦的UL双连接,但对于给定的级联子案例k,主要和次要UL的SINR覆盖概率分别由式(37)和式(38)给出: (τP,τS,k) = (37) ∫∞0e-τ'Sσ2(PUE )-1rαe-∑m∈{M,P,F}πλm (τ'S)2αr2∫∞0du1+uα2fRkOSr dr (38) UL 覆盖概率为: PNOMA-C(τP,τS,k) = (39) 总平均UL 覆盖概率为: (40) 由此得到NOMA系统的UL覆盖概率,其使用传统的基于DRSP的CUDA准则,这由推论1给出。 推论1对于所考虑的3层DC HetNets,当在NOMA方案中运用基于DRSP的CUDA准则时,总平均概率为: (41) 基于之前的数学分析,本节给出了仿真和数值结果分析,以说明所提出的基于NOMA和DUDA的多层HetNets的性能。为了不失一般性,考虑了一个由MBS、PBS和FBS组成的3层HetNet,且假设整个网络的路径损耗指数完全相同。仿真环境为宏小区半径500 m,载波频率2.4 GHz,系统带宽20 MHz的区域,所有接收器处的加性高斯噪声功率相同。除非另有说明,取PP=29 dBm,PF=24 dBm,λM=1/π5002,λP=5λM及λF=10λM;功率限制PM>PP>PF总有效,UE的传输功率为PUE=26 dBm。 Table 1 Association probability under different powerPM(α=4.3) 图2进一步研究了取路径损失指数α=4.3和α=3.3时,MBS、PBS和FBS的传输功率PM、PP和PF对条件级联概率的影响。可以看到,虽然传输功率PM和PF对级联概率PSC1有明显影响,但传输功率PP对其影响非常有限。从图2c可以看出,在PP的整个变化范围内,级联概率PSC1几乎不变。同时,传输功率PM、PP、PF对PSC2和PSC3具有不同的影响。图2表明,PSC1、PSC2、PSC3的总和满足总概率定律。同时,该图还反映了路径损耗指数α对条件级联概率的影响,PSC2不仅随路径损耗指数单调变化,还受传输功率影响,如当PM较小时,PSC2随着α的增大而减小,当PM较大时,PSC2随着α的增大而增大。对于SC1,该情况下条件级联概率随着路径损耗指数的增加而增大;SC3级联场景下,路径损耗指数越大,条件级联概率越小。 Figure 2 Conditional association probability vs transmission power图2 条件级联概率vs传输功率 除了传输功率外,BS的密度对级联概率也产生了很大影响。取PM=46 dBm,PP=42 dBm,PF=34 dBm,图3a和图3b分别表示密度比λP/λM和λF/λM相对级联概率PSC1、PSC2、PSC3的变化趋势。比较图2和图3可发现,虽然BS的传输功率对级联概率有明显影响,但BS的密度对其影响很小。尤其是,图3a显示级联概率PSC1在λP/λM的整个区域恒定近似,级联概率PSC2随密度比λP/λM的增加而减小,PSC3随着密度比λP/λM的增加而增长。对于这些观测,有以下解释。首先,从图1可知,级联子案例1由M层和F层所主导,这导致密度λP对PSC1的影响有限。不同于子案例1,子案例2利用解耦UL和DL级联,其中上行链路取决于P层,显然,密度λP越大,P层的BS接近给定UE的概率越高,因此解耦的级联概率PSC2随着λP的增大而降低。虽然子案例3也利用了DUDA,但是这种情况将次要UL与P层最近的BS相级联。显然,密度λP越大,级联概率PSC3越高,级联概率PSC3随着密度λP的增加而增加。 Figure 3 Conditional association probability vs density ratio图3 条件级联概率vs密度比 与图3a不同,图3b表明随着λF/λM的增加,条件级联概率PSC2增加,条件级联概率PSC3减小。这是因为子案例2将主要UL与F层最接近的BS相级联,这导致解耦的级联概率PSC2随λF的增加而增加。虽然解耦的子案例3将主要UL与F层相级联,然而其也将次要UL级联至P层与F层。显然,随着λF的增加,从给定UE到P层最近BS的距离的概率为二阶统计量,且高于给定UE级联至F层最近BS的概率,因此解耦的级联概率PSC3随着λF的增大而减小。 为了突出DUDA的优点,本文还对比了DUDA和CUDA准则之间的总平均覆盖概率和频谱效率。取功率分配因子αp=3.5,从图4a可以看出,当考虑覆盖概率时,具有DUDA的NOMA方案优于传统的CUDA方案。此外,可实现的覆盖概率增益随着路径损耗指数α的减小而增加。这是因为在本文的系统模型中,解耦UL级联是基于最近距离准则执行的,因此最近的传输距离的覆盖性能损耗较少。该结果表明结合DRSP和UL最近距离解耦级联方案是有效的,从而实现了更高的覆盖概率增益。图4b中比较了不同路径损耗指数下DUDA和CUDA的频谱效率SE。首先可以发现,在NOMA模式中,SE间隙是变化的,并且随着发射功率的增加而增加。其次,图4b显示当路径损耗指数增大时,DUDA可实现的总平均SE高于CUDA的总平均SE。然而,当路径损耗指数较小时,CUDA的SE高于DUDA的。该结果表明,DUDA相对于CUDA获得的SE增益在很大程度上取决于路径损耗指数。当路径损耗指数大时,基于DUDA的NOMA优于基于CUDA的NOMA,当它很小时,基于DUDA的NOMA方案不如基于CUDA的NOMA方案。 Figure 4 Comparison between DUDA and CUDA whenαp=3.5图4 αp=3.5时DUDA和CUDA间的对比 基于DUDA和DC技术,本文研究了NOMA方案3层HetNets模型可实现的覆盖概率和频谱效率。使用跨层DC充分利用网络资源,同时采用DUDA方案,让用户在UL和DL中使用不同的级联标准,并且UE同时级联至2个不同层的接入点。对于此HetNets模型,首先,在严格的DL级联约束下研究了可行的解耦UL级联方案,并阐述了3种可能的级联子案例。其次,数学推导了每个解耦级联子案例的条件级联概率,以及主要和次要接入距离的相应统计级联。 最后,基于条件级联概率,推导了系统的覆盖概率,利用数值结果验证了级联概率的解析表达式。研究结果表明,在覆盖概率方面,基于DUDA的方案性能优于传统的CUDA方案。研究还发现,基于DUDA的方案的频谱效率是否优于基于CUDA的方案的频谱性能受功率分配因子和路径损耗指数的影响。研究结果有助于指导多层异构网络的设计。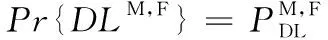
3.2 主链路-F层,次链路-M层

3.3 主链路-F层,次链路-P层
4 主要和次要UL接入距离的统计描述
4.1 主链路-M层,次链路-F层

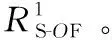

4.2 主链路-F层,次链路-M层

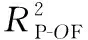
4.3 主链路-F层,次链路-P层
5 NOMA的覆盖性能


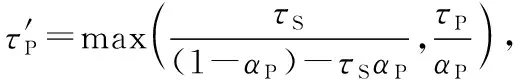



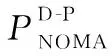
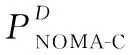


6 数值结果及仿真分析
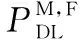



7 结束语
