基于多块体的非对称双层临坡地基上限承载力

杨博铭

（湖南大学设计研究院有限公司，湖南长沙410082）

临坡地基承载力，既可看作地基极限承载力问题，也可看作边坡整体稳定性问题.临坡地基与水平地基的区别在于：临坡地基的承载力受到坡体的几何特性以及边坡土体的物理力学性质的共同影响和制约.因此推导能综合考虑临坡地基影响因素的承载力计算方法是解决工程实际问题的有效途径.

目前，在进行临坡地基设计时，没有相关规范可以参考，绝大多数工程问题都是采用在水平地基极限承载力公式的基础上乘以一个修正系数的方法[1].这样的经验计算方法的可靠性、合理性以及经济性在一定程度上很难实现定量把控[2-3].关于临坡地基极限承载力研究，可分为以下三类：第一类是在平地地基的基础上进行研究[4-6]，考虑坡面倾斜系数来进行折减修正，其计算简单，力学理论清晰明了，但是折减系数的确定没有理论公式支持，仅根据经验取值，缺乏一定的科学性.第二类就是直接以临坡坡体为研究对象，充分考虑其破坏模式的非对称性，但是其理论基础还是固体介质力学，这样导致计算结果与工程实际存在一定差距[7-8].第三类就是通过实验来处理工程问题[9-11].虽然实验的结果与工程实际更加接近，但是造价以及时间成本是制约其发展的主要因素.上述极限承载力计算方法，在工程应用中计算值可能过于保守，造成浪费，或者因承载力不足而导致工程事故.综上，完善临坡地基设计理论、计算方法，在保证建筑物安全的前提下，优化工程设计参数、降低工程造价具有重要的经济效益和社会效益.

在临坡地基破坏机理、破坏模式研究方面，Kusakabe 等[12]、Mizuno 等[13]认为临坡地基单侧破坏模式的破坏机构由3 个滑块组成，即基础下的三角形主动破坏区、中间过渡区和被动滑块区，且认为基础底下的主动区为对称的三角形.但是，对于中间过渡区，不同学者又有不同的观点，Kusakabe 认为是对数螺旋线而Castelli 等认为是圆弧滑动面并延伸到坡面[14]；对于主动破坏区，王晓谋等[15]利用有限元法提出基础底下的弹性区应为不对称的三角形.同时魏学勇等[16]还提出应该考虑基础内侧土体应力分布对基础承载力的影响.

对于非均质的临坡地基承载力的研究，部分学者给出了相应的研究方法.胡卫东等[17]考虑了临坡地基的分层性以及非对称性，但是没有考虑到内摩擦角对临坡地基承载力的影响，也没有考虑基础与土体之间的相对滑动对承载力的影响；秦会来等[18]考虑了地基的分层特性，但其计算方法是基于水平地基的.因此，本文在条形基础荷载作用下，将多块体理论运用于临坡地基，考虑临坡地基破坏模式的非对称性与地基土体的成层性，同时考虑了土层分层界面处上、下土层的速度间断性，以及基础与土体之间的相对滑动，来建立临坡地基的多块体破坏模型及其相应允许的速度矢量场.引入极限分析理论，推导了非对称双层临坡地基上限承载力计算方法.

1 临坡双层地基破坏模式的确定

1.1 多块体上限分析法

多块体上限分析法是极限分析法的一种，其基本理论为：对于任何运动许可的破坏机构，其内能耗散率可用式（1）进行描述[19].

式中：Ti为边界面S 上面积分布力矢量；Xi为区域V内体积力矢量；εij是基于运动许可速度场的塑性应变率场；σij是满足流动法则并与εij相关联的应力场；vi是运动许可速度场，即与εij满足几何相容的速度场.

在本文计算模型中，外力功的功率应包括：重力功的功率、基础传递荷载功的功率和考虑埋深的超载功率；对应的内能耗散的功率应包括：块体间速度间断面的内能耗散率和基础底面摩擦消耗的内能.

1.2 双层临坡地基中多块体上限法的破坏模式

破坏模式决定了相容速度场的分布从而决定了内能耗散率.相比于双侧破坏模式，单侧破坏模式计算临坡地基承载力偏于安全，且与工程实际更加接近.为了能够充分体现分层界面处速度的间断性，本文采用如图1 所示的破坏模式，并建立如图1 所示的坐标系：基础中心点O 为坐标原点，水平向右、竖直向下分别为x 轴、y 轴正方向.

如图1 所示，根据临坡地基单侧破坏机理，破坏模式由n 个刚性三角形组成.为便于叙述，分别做如下规定：滑动面记为A123456…n，沿着滑动面上的节点1、2、…、n 记为外部节点；外部节点与坐标原点相连的线段称为主斜线（如O71）；水平地层分界线与主斜线的交点用n+1、n+2、2n 来标记，记为内部节点；条块标示用①②③…表示，条形基础正下方的三角形条块为条块①；连接主斜线的线段称为辅斜线（如72）；位于滑裂面上的辅斜线称为底辅斜线（如12）；滑动面上的 n 个大三角形（△O12、△O23…）以原点为顶角，且顶角分别设定为 α1、α2、α3…；底辅斜线与竖直线的夹角（顺时针）为 β1、β2、β3…；破坏面上的底辅斜线长为 c1、c2、c3…；辅斜线长为 p1、p2、p3；主斜线长为 l1、l2、l3.

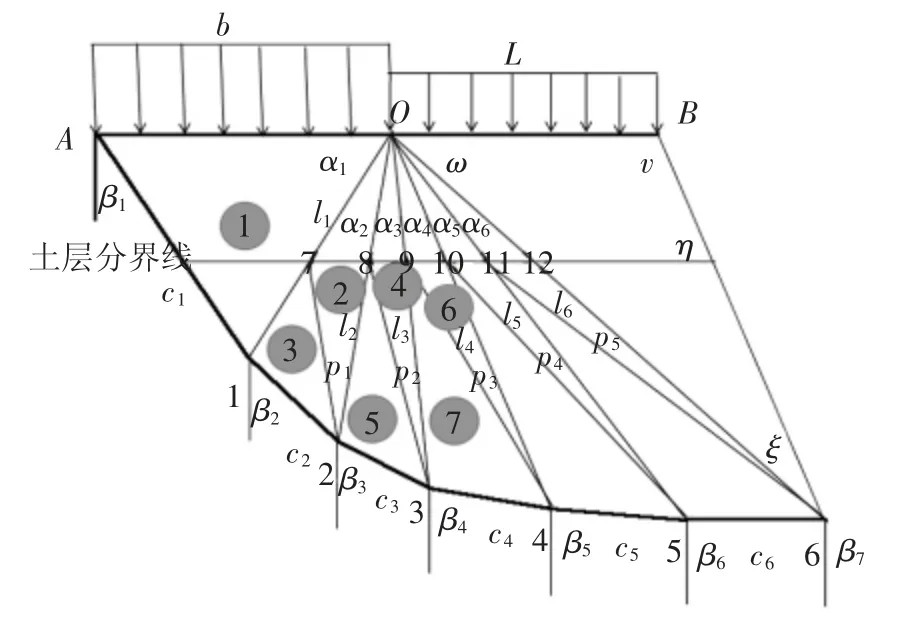
图1 破坏模式Fig.1 Collapse model

在图1 中，对于水平层状土，若主斜线li位于两层土中则其长度分别表示位于上层土的长度和位于下层土的长度.大三角形被辅斜线分为两个三角形，三角形编号如图1 所示，三角形的面积分别表示为S1、S2、S3….土层分界线将偶数编号的三角形面积分为上、下层土的面积之和即Si=为上层土中三角形的面积，为下层土中的面积.编号为奇数的三角形都位于下层土中，下层土中四边形面积被辅斜线分为左右两个三角形，分别用表示其面积.

1.3 几何参数的求解

已知条件：条形基础的宽度d、基础外沿距坡顶距离 l=ad（a 为距离比系数）、可变参量 αi和 βi、上层黏土的厚度h.根据图1 所示几何关系，可分别求出其他几何参数.

主斜线长度见式（2）.

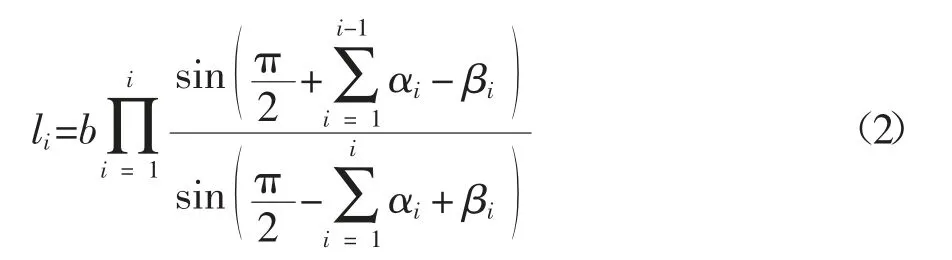
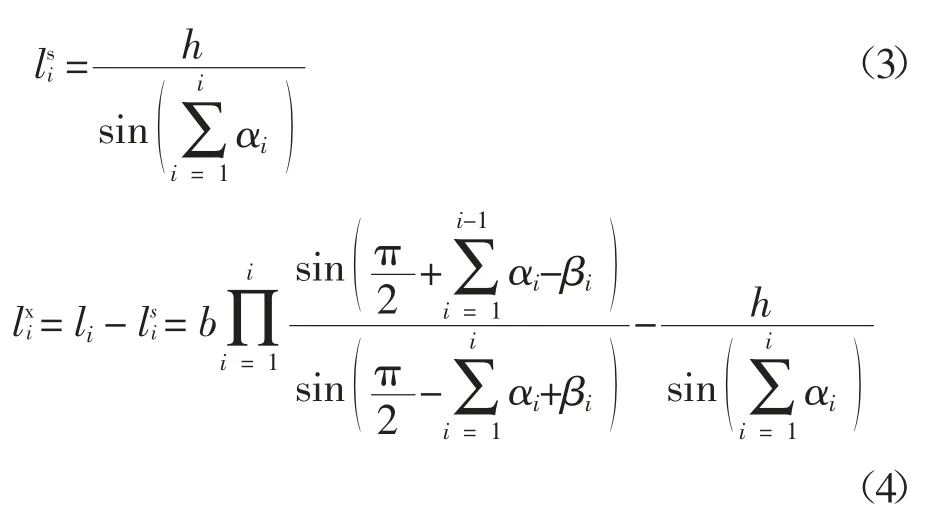
底辅斜线长度 ci见式（5）（6）.

当 i>2 时采用式（7）计算.

对于条形基础下的三角形滑块1，如果土层分层线通过底辅斜线A1 时，同理可将A 1 的长分解为.

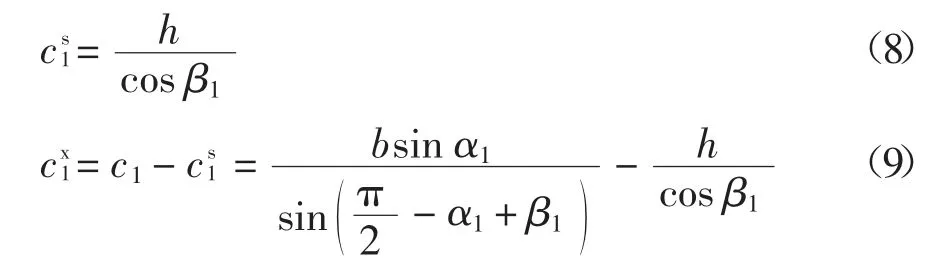
辅斜线的长度为Pi，由余弦定理：a2+ b2- 2ab cos C=c2，可以推出 pi，见式（10）.

大三角形滑块的面积 Sαi见式（11）.

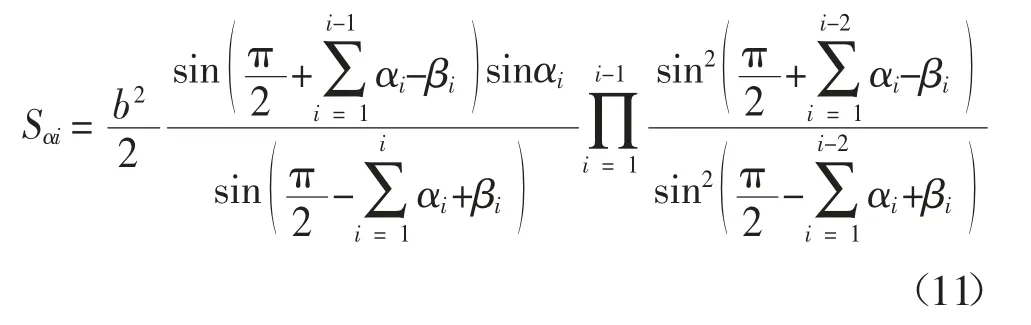
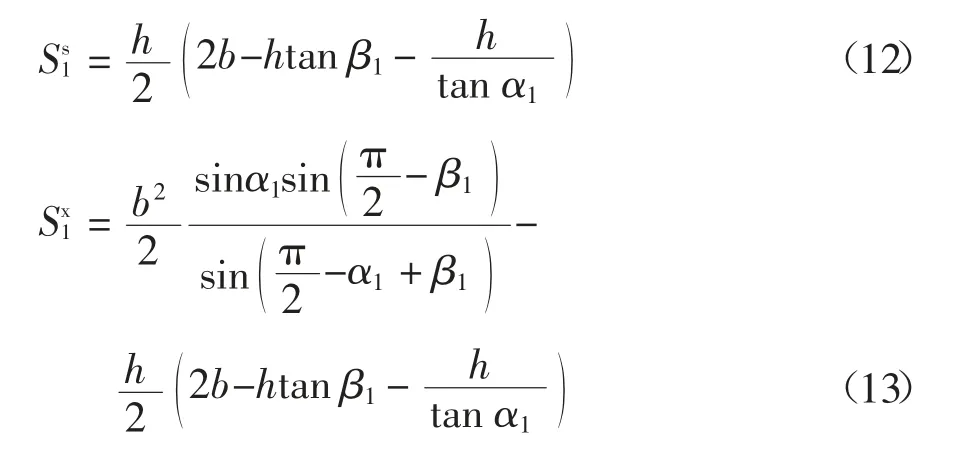
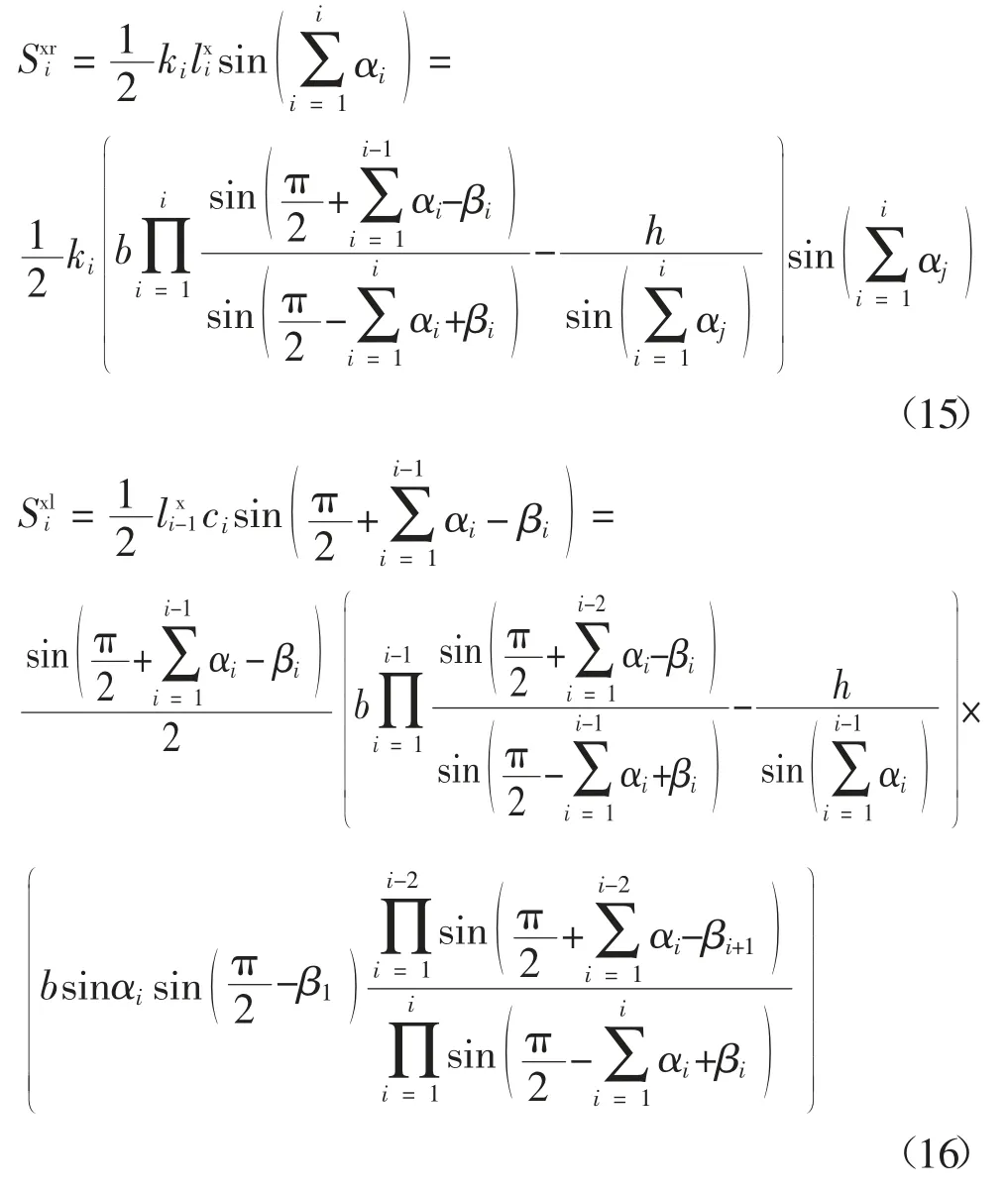
当i 为偶数时：

当 i 为奇数且 i ＞ 1 时：

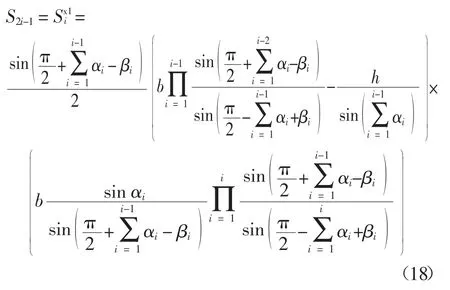
边坡表面倾斜且无限延伸，坡角为η，则边坡表面最外侧的三角形滑块，根据几何关系即可确定其几何参数，如图1 所示三角形内角分别为ξ、ω、υ，三者之和为180°.

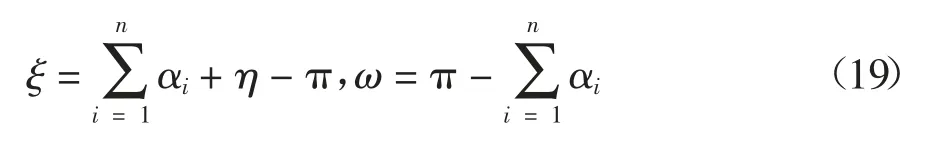
上述分析过程，构建出了条形基础下的非对称临坡双层地基的多滑块破坏模型.该模型既能充分反映地基破坏时的非对称性，又能充分体现在地基分层界面处块体的速度间断的特性，为本文计算临坡分层地基在条形基础荷载作用下的极限承载力的合理性打下基础.与此同时，为了保证单侧滑块的破坏模式的形成，块体的几何条件应满足下述条件的约束：滑块顶角总和应等于π-ω，当临坡地基无限接近水平地基时，ω 为0，滑块顶角总和为π；为保证计算精度，将临坡地基分为n 个刚性三角形（n ＞1），即αi＜π/2；当临坡地基无限接近水平地基时ξ 为0，因此 ξ ＞ 0.

2 机动允许速度矢量场的确定

2.1 基本假定

根据条形基础下的临坡地基的几何参数，以及本文研究的具体情况，在确定临坡双层非对称地基承载力上限值所允许的速度矢量时，做如下假定：

1）土体服从Mohr-Coulomb 屈服准则以及相关流动法则；

2）考虑条形基础基底和土体的相对滑动，其外摩擦角为δ；

3）基础在上部荷载作用下向下做垂直运动；

4）土层分界面为水平向.

2.2 速度的确定

根据假设以及速度相容原理，求得各滑块的速度以及间断面的速度.

1）根据图2 所示速度关系，在条形基础下方的三角形滑块的速度以及间断面的速度见式（23）.

式中：v1为滑块1 斜向下的移动速度.

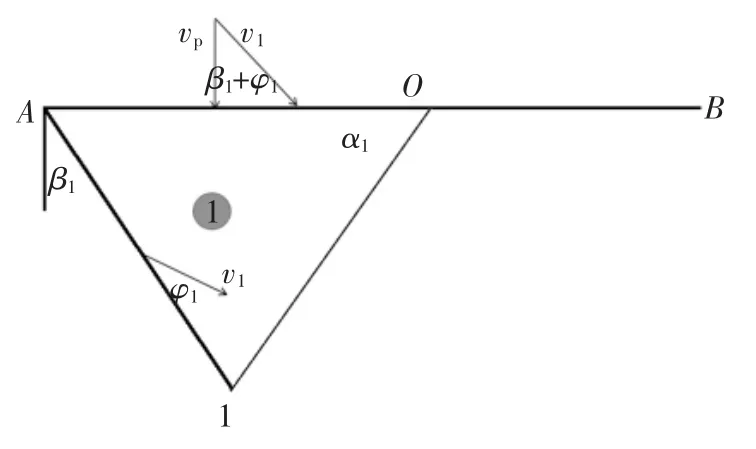
图2 块体1 速度相容矢量场Fig.2 Compatible velocities of block 1

在A1 间断面上v1为间断面速度，其方向与A1边的夹角为该土层的内摩擦角.

2）根据条块1 的速度来求条块3 的速度.滑块1和滑块3 之间的相容矢量关系如图3 所示.

式中：v3相对于竖直线夹角为β2+φ2.

图3 三角滑块1、3 的相容速度矢量场Fig.3 Compatible velocities between block 3 and 1

同理，可得滑块 5、7、9、…、i…的速度.

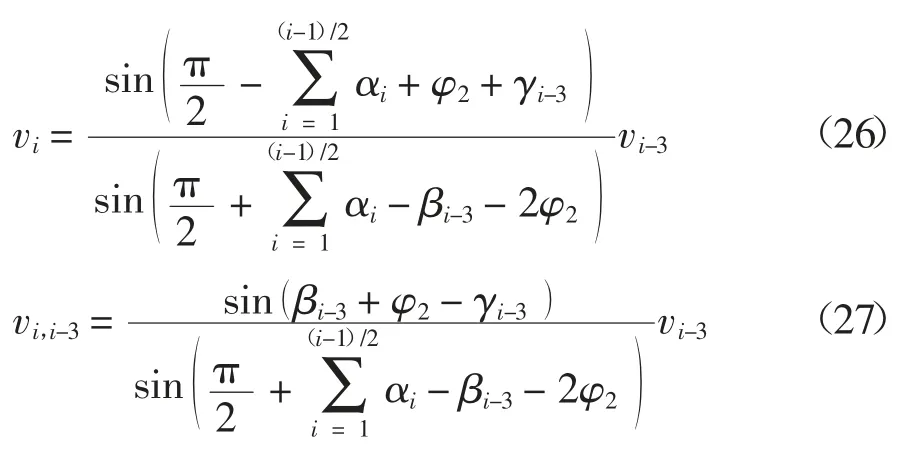
根据滑块1 和滑块3 的速度，求出滑块2 的速度，其中γ2为中间变量，是滑块2 的速度与竖直方向的夹角，可以利用求出，然后再代回式中即可求得滑块2 的速度.其矢量关系如图4 所示.

式中：x2为辅斜线相对于竖直线的夹角.

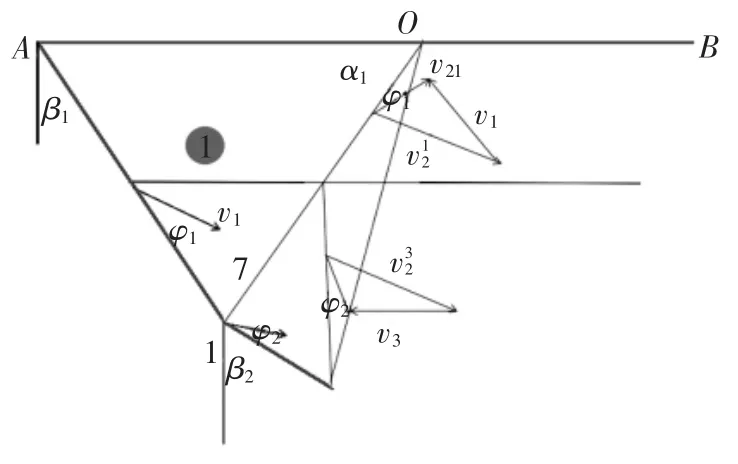
图4 速度关系Fig.4 Velocity relation

同理，根据滑块2、5 的速度，可求出滑块4 的速度.

根据以上关系，写出一般式，见式（36）～（39）.

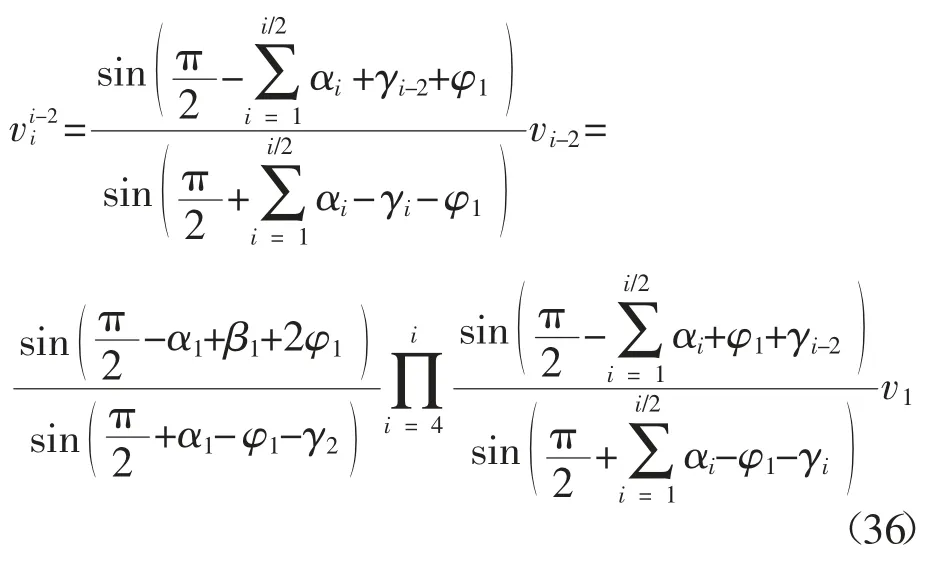
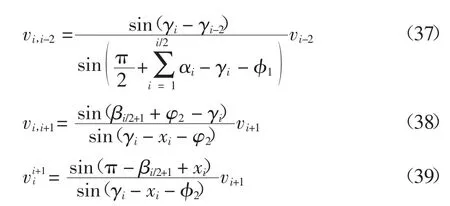
在求三角形的速度时应该按照 1，3，2，5，4，7，6，…的顺序来求解.

3 功率消耗计算

3.1 外力功率的计算

计算模型中的外力包括：基础埋深引起的附加均匀分布应力、基础底面的极限压应力和块体的自重.

1）基础埋深引起的附加均布应力q 的功率Wq见式（41）.

其中不考虑基础埋深内土体的抗剪强度对承载力的影响，ρ1为第一层土体重度，H 为基础埋深.

2）基础传递下来的极限压应力Qm的功率WQm见式（43）.

滑块1 土层1 中的自重外力的功率见式（44）.

滑块1 土层2 中的自重外力的功率见式（45）.

4）其余滑动块的自重外力功率.

i=3，5，7，…时滑块自重功率 Wxlsi见式（48）.

靠近斜坡的滑块自重的外力功率Wsn+1见式（49）.

综合上述计算所得外力功率，总功率记为B.

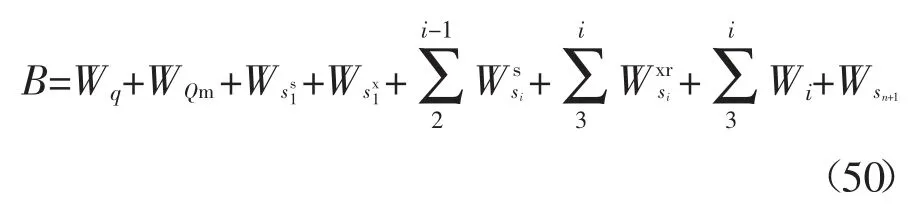
3.2 内能耗散率计算

内能耗散率主要考虑到速度间断面、基础和土体的接触面、滑动破坏面上的能量耗散.

滑块间断面的内能耗散率：主斜线lsi、lxi辅斜线Pn.

滑动面上的间断面的内能消耗：底辅斜线ci.

综上所述，总的内能耗散率记为A.

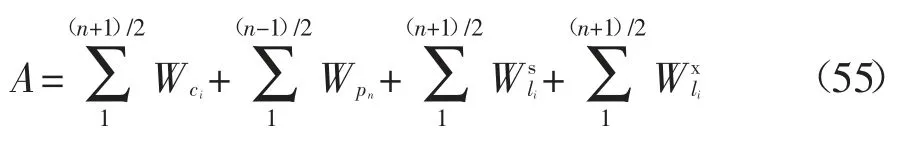
4 非对称双层临坡地基极限承载力上限解

极限分析法，是将岩土体看作刚体，利用连续介质中的虚功定理来推求岩土极限荷载的上下限解[20].上限定理又叫能量法，首先假设一个滑裂面，构建一个位移场，然后根据虚功原理求解极限荷载，使得外荷载功率和内能耗散功率相当[21].根据本文所选取的地基破坏模式、机动允许的速度场，由上限分析理论可得上限解，见式（56）.

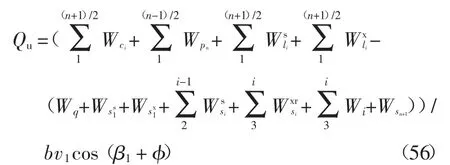
要使临坡地基取得极限承载力Qu的最小值，只有当地基处于极限状态，即式（56）取最小值.利用Matlab 编程计算可获得承载力的目标函数表达式，即将问题转化为约束非线性规划问题.对式（56）进行优化求解必须满足式（22）的约束条件，本文采用序列二次规划算法（SQP）.SQP 非线性优化算法是利用目标函数和约束条件构造增广目标函数，借此将约束最优化问题转化为无约束最优化问题，然后利用求解无约束最优化问题方法间接求解新目标函数的局部最优解问题，此方法既适合高度非线性问题，也具有较快的运算速度[22-24].

5 工程算例计算与分析

为了验证本文关于非对称双层临坡地基上限承载力计算方法的合理性，结合具体工程案例进行分析，并与相关的分析方法、软件计算结果进行对比.验证的具体情况如下.

5.1 算例1

采用文献[17]中的计算案例：某临坡条形基础双层地基，基础埋深H=1.0 m，持力层范围内两层饱和黏土.土体相关计算参数详见文献 [17].基础外边缘到基础坡顶的距离l=a×b，其中a 为距离比例系数，a=1，边坡坡角 η =20°.5.1.1 计算结果对比分析

文中还采用有限差分软件（FLAC-3D）对工程案例1 的非对称临坡地基进行数值计算.在分析过程中按平面应变问题处理，材料参数：E = 45 × 103kPa，ν=0.3.土体的本构模型服从 Mohr-Coulomb 屈服准则.图5 为分级加载的荷载-位移曲线，每一级荷载为10 kPa.

图5 分级加载沉降曲线Fig.5 Graded loading sedimentation curve

图5 所示为FLAC 模拟的分级加载的荷载-位移曲线，可以看到，当加载到110 kPa 时位移呈极速下降的状态，通过观察塑性区可看出，此时塑性区已经贯通.而文献[17]中采用Abaqus 得到的荷载-位移曲线得出破坏荷载也应该在110 kPa 左右，此时荷载-位移曲线已经处于快速下降阶段，在文献[17]中作者的取值有些偏大.

表1 计算结果比较Tab.1 Comparison of computation results

数值模拟结果表明，案例1 中的双层地基加载到Qu=110 kPa 时临坡地基发生了破坏.文献 [17]的理论计算方法所得地基极限承载力Qu=128.6 kPa，本文所得地基极限承载力Qu=125.9 kPa，两者的计算结果与数值分析结果都很接近，很明显本文结果更加接近数值分析结果.在多滑块体分析模型中，块体划分得越细其计算值就越精确，本文的块体划分比文献[17]中的块体数量少了一半，但计算结果比文献[17]中的计算值更加接近于数值分析结果，因此本文的分析方法可行且效率更高.

5.1.2 参数分析与讨论

分层地基的承载力一般会受到土层性质、土层厚度的影响.通常，下卧软弱土层都对基础承载力有不利影响.为了探讨上、下层土的强度参数以及几何尺寸对基础的极限承载力的影响规律，下文通过改变案例1 中的下卧层土的黏聚力，其他参数保持不变，来分析土体强度参数的改变对承载力的影响；在保持强度参数不变的情况下改变上层土体的厚度来分析土层厚度对承载力的影响.

图6 所示为在不同的上层土体厚度情况下，土体黏聚力对承载力的影响曲线.由图6 可知：随着下层土体黏聚力的增加，临坡条形地基的承载力上限值也逐渐增加且增加速度越来越快.在上层土厚度不同的情况下，上、下层土体强度差距越小，其地基的承载力也就越接近，这与事实相符.当上、下层土体强度逐渐接近时，不管上层土的厚度是多少，其地基承载力趋近于同一个值，即接近于均质地基承载力.

图7 所示为临坡条形基础的上限承载力与上层土厚度的关系，图中给出了上、下土层不同黏聚力的承载力随着上层土的厚度变化的关系.当两层土体强度相差不是很大时，随着上层土厚度的增加，地基承载力也增加.当土层厚达4 m 左右时，承载力不再受黏聚力比的影响，即转化为单层土体的地基承载力形式.两层土体的强度差异很大时，其承载力依然随着厚度增加而增加.

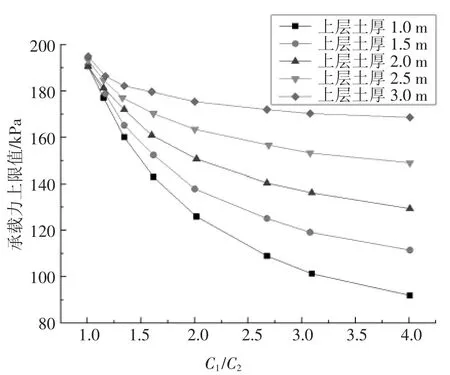
图6 上限承载力和黏聚力比的关系Fig.6 Relationship between upper bearing capacity and cohesion ratio

图7 上限承载力与上层土厚度的关系Fig.7 Relationship between upper bearing capacity and upper soil thickness

5.2 算例2

为进一步验证本文计算理论的正确性和合理性，下面采用不分层的临坡地基来计算地基上限承载力.一临坡地基，基础宽b=2 mm，坡顶距比a=0，基础埋深2 m，重度γ=18 kN/m3，内摩擦角φ=π/6，黏聚力C=20 kPa，坡角η=π/9.计算结果和文献[17，25-26]计算结果对比见表2.

表2 计算结果比较（a=0）Tab.2 Comparison of computation results（a=0）

算例2 是非成层地基，而本文计算方法主要针对分层地基，但是本文计算方法可以退化为均匀地基来计算临坡地基的承载力上限值.计算结果与其他3 种理论计算方法对比表明：本文采用较少的计算单元（10 个计算单元）获得了与其他文献相近的承载力值.综上，本文采用较少的单元划分，得到较好的计算结果，证明了本文采用的破坏模式是合理、有效的.

6 结 论

本文综合考虑了地基的分层性、破坏的非对称性、基础与土体的摩擦作用、地基埋深、基础外缘与坡顶距离等对临坡地基承载力的影响.采用一种新的多滑块模式来构建其破坏模式并根据速度相容的关系、速度三角形闭合条件确定该模型的相容速度场，同时采用极限分析法的上限分析理论来推导双层临坡地基上限承载力的计算公式.最后，通过两个算例，分别与数值分析结果和理论计算结果对比，证明了本文计算方法的合理性，并进行参数分析，得出如下结论：

1）随着下层土体黏聚力的增加，临坡条形地基承载力上限值也逐渐增加且增加得越来越快.

2）当两层土体强度相差不是很大时，随着上层土厚度的增加，地基承载力也增加.当土层厚达4 m左右时，承载力不再受黏聚力比的影响，即转化为单层土体的地基承载力形式.两层土体的强度差异很大时，其承载力依然随着厚度增加而增加.