水泥土强度特性和损伤本构模型研究

陈鑫 ，张泽 ，李东庆

（1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000；2.中国科学院大学，北京100049；3.东北林业大学寒区工程与科学技术研究院/土木工程学院，黑龙江哈尔滨150040）

地层改良是冻结法施工中防治冻胀融沉的重要措施[1-2]，如港珠澳大桥珠海连接线拱北隧道口岸暗挖段采用管幕冻结作为预支护时，对管幕周边采用预先注浆土体改良法来控制冻土帷幕的冻胀融沉[3].改良土体在冻结法实施期间处于冻结状态.此外，地层改良广泛应用于季节冻土区和多年冻土区的路基工程和深基础工程中[4-5].寒区地表存在着一层冬冻夏融的冻结-融化层，改良土暴露于自然环境下，每年都有很长的时间处于冻结状态.为促进地层改良在控制冻胀融沉和寒区工程建设中的推广应用，就有必要深入系统研究改良土的力学特性，尤其是对处于冻结状态下的改良土力学特性的研究.

水泥是地层改良中广泛使用的固化剂，把水泥掺加到地基中，使水泥与地基土发生物理、化学反应，从而使地基土得到固化形成水泥土.国内谭丽华[6]最先对冻结水泥土的单轴抗压强度进行研究，考察了土性、水泥掺量、温度对冻结水泥土单轴抗压强度、弹性模量和泊松比的影响.随后胡俊等学者[7-9]也对冻结水泥土的单轴抗压强度进行了研究，考察的因素主要有土性、水泥掺量、温度、养护龄期、水灰比.已有研究结果均表明水泥土的单轴抗压强度随温度降低和水泥掺量增加而增大，随养护龄期的增加也呈增大趋势，王许诺等[10]还对各影响因素的重要性进行了研究，指出温度对水泥土力学特性影响最大.于学敏[11]通过室内直剪试验研究了含水量、水灰比、养护时间、温度对注浆、冻结后粉细砂抗剪强度的影响，给出了各因素与试样抗剪强度值之间的关系.游小锋等[12]通过一系列低温三轴剪切试验研究了冻结温度、水灰比、含水量、养护时间、围压对冻结水泥土抗剪强度及割线模量的影响，结果表明抗剪强度与割线模量均随冻结温度降低而增大，与水灰比、含水量、养护时间呈正比关系.张向东等[13]首先通过室内单轴压缩试验及冻胀量确定出风积砂中最优水泥掺量，通过动力循环试验研究了水泥改良风积砂在负温下的动力参数.牛亚强等[14]对黄土、水泥改良黄土及石灰改良黄土进行了-6 ℃下的三轴压缩试验，围压取1～15 MPa，研究了围压对冻结黄土和冻结改良黄土的强度和变形特性的影响，建立了能够描述冻结黄土及冻结改良黄土的强度随围压变化的非线性莫尔-库仑强度准则.

从以上研究可以看出，目前关于冻结状态下水泥土强度的研究主要集中在单轴抗压强度方面，对其三轴抗剪强度的研究较少，且同样是考察归纳各因素对其强度的影响规律，研究深度不足.岩土材料的变形破坏过程就是损伤不断累积的过程.张土乔[15]考虑到水泥土的应力-应变关系受水泥掺量、养护龄期、围压的影响表现出不同特征，基于连续介质损伤力学建立了能够反映水泥土加工软化、加工硬化和脆性三种应力-应变特征的损伤本构模型和损伤变量演化方程.童小东等[16]基于连续介质损伤力学和不可逆热力学理论建立了水泥土弹塑性正交各向异性损伤本构模型，陈慧娥[17]在此基础上考虑有机质的影响，建立了耦合有机质作用的损伤变量演化方程.王立峰等[18]在应力主轴与材料主轴重合且在加载过程中保持不变的假定前提下建立了损伤本构模型，通过单轴加卸载试验确定了模型中参数.

以上关于水泥土损伤本构模型的研究均是基于室温状态，考虑到目前对冻结状态下水泥土受荷损伤特征研究较少，本文首先进行了室温和冻结状态时不同围压下水泥土三轴剪切试验（室温状态作为对照），考察了围压对水泥土力学参数影响规律，建立了能够反映出低围压对冻结水泥土强度的强化作用和高围压的弱化作用的修正Hoek-Brown 强度准则.之后假设水泥土微元强度的分布规律服从双参数的Weibull 函数，基于非线性的Hoek-Brown 强度准则和其修正形式分别确定室温和冻结状态下水泥土微元强度F，损伤本构模型中的参数通过室温和冻结状态下三轴试验数据确定，最后利用围压对Weibull 函数中的形状参数和尺度参数进行修正，建立了考虑围压的统计损伤本构模型，通过与试验曲线对比讨论其适用性.最后讨论了损伤变量随轴向应变和围压的演化规律.

1 三轴剪切试验方案

1.1 试样制备

试验用土取自兰州市，其基本物理性质指标：最优含水量为16.2%，最大干密度为1.74 g/cm3，塑限wP=15.6%，液限wL=27.7%，塑性指数IP= 12.1.土样的颗粒级配曲线如图1 所示.

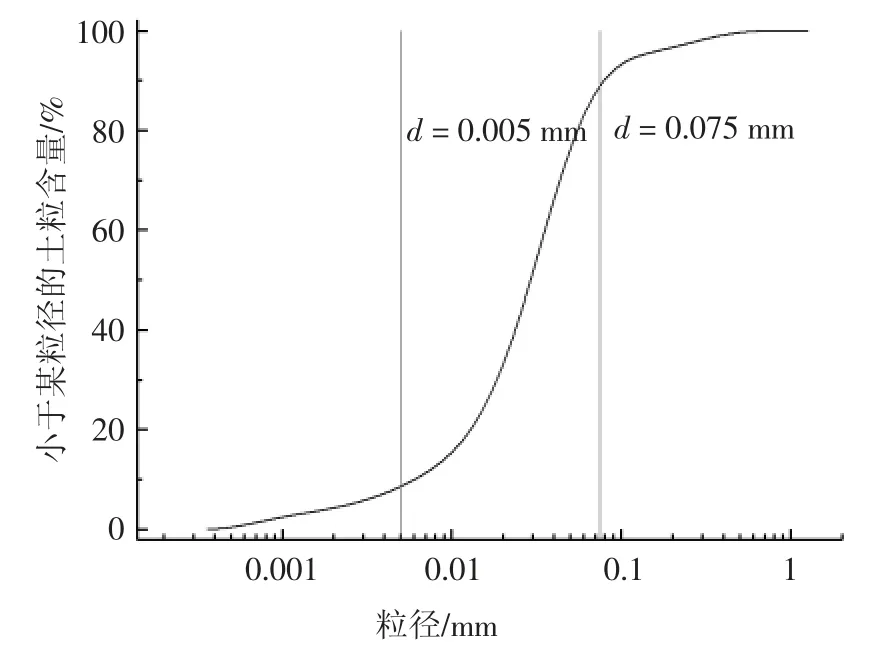
图1 试验土样颗粒级配曲线Fig.1 The particles gradation curve

试验所用水泥为青海水泥有限公司生产的昆仑山PC32.5.将试验所用土样风干、碾压、过2 mm 筛，测定过筛后土样的含水率.根据《水泥土配合比设计规程》（JGJ/T233—2011）中规定的水泥掺量范围3%～25%[19]，同时参考相关文献研究取值[20]，试验设计水泥土中水泥掺量取15%，初始含水量为22.2%，初始干密度为1.6 g/cm3.制样时先根据水泥掺量计算出所需的干土和水泥质量，然后充分搅拌均匀，最后加入所需的去离子水后再搅拌.严格控制整个制样过程在30 min 内完成.将制好的试样用保鲜膜包裹，放入恒温箱中养护7 d.随后将试样装模，放入饱和缸进行抽真空饱和，确保试样饱和度在95%以上.

1.2 试验方法

试验设定室温（+20 ℃）和负温（-5 ℃）两种温度，分别研究室温和冻结状态下水泥土三轴压缩强度.试验仪器采用冻土工程国家重点实验室的MTS-810 低温材料试验机，其最大轴向荷载为50 kN，最大围压为20 MPa，温度控制范围为-25 ℃～40 ℃.将饱和后的部分试样直接在室温状态下进行不同围压下的三轴剪切试验，考虑到地层改良实际施工扰动的影响，如采用注浆改良地层时的压密作用，将围压设定为 0.25、0.5、0.75、1.0 MPa 共 4 个水平.将其余试样和模具置于-25℃的恒温箱中迅速冻结48 h，然后拆模将试样两端用环氧树脂垫片固定，外层套乳胶膜，最后放入-5 ℃恒温箱静置12 h 使试样达到设定温度.考虑到冻结过程中冻胀应力的影响，冻结状态下围压设定为 0.5、1.0、1.5、2.5、3.5、5.0、7.0 MPa 共7 个水平.施加围压后的试样在设定条件下固结2 h，随后以0.125 mm/min 的加载速度施加轴向荷载.应力-应变曲线出现峰值时继续加载一段时间结束试验；无峰值时，试样产生20%应变结束试验.

2 试验结果分析

2.1 变形特征

图2 为室温和冻结状态水泥土在不同围压下偏应力-轴向应变曲线.

从图2 中可以看出，当轴向应变较小时，室温和冻结状态下偏应力随轴向应变增大近似呈线性增大，随后过渡到弹塑性阶段.室温状态下试验设定围压较小，偏应力-应变曲线均表现出明显的应变软化现象.冻结状态下水泥土偏应力-应变曲线形态受围压影响明显，围压小于3.5 MPa 时，其应力-应变关系表现出明显的应变软化现象；围压大于等于3.5 MPa 时，其应力-应变关系则呈应变硬化现象.室温和冻结状态下施加不同围压时水泥土偏应力-应变曲线可用文献[21]提出的改进邓肯-张模型描述，拟合线示于图2，该模型表达式如下：

式中：a1、a2、a3随围压变化而变化，单位均为 MPa-1.

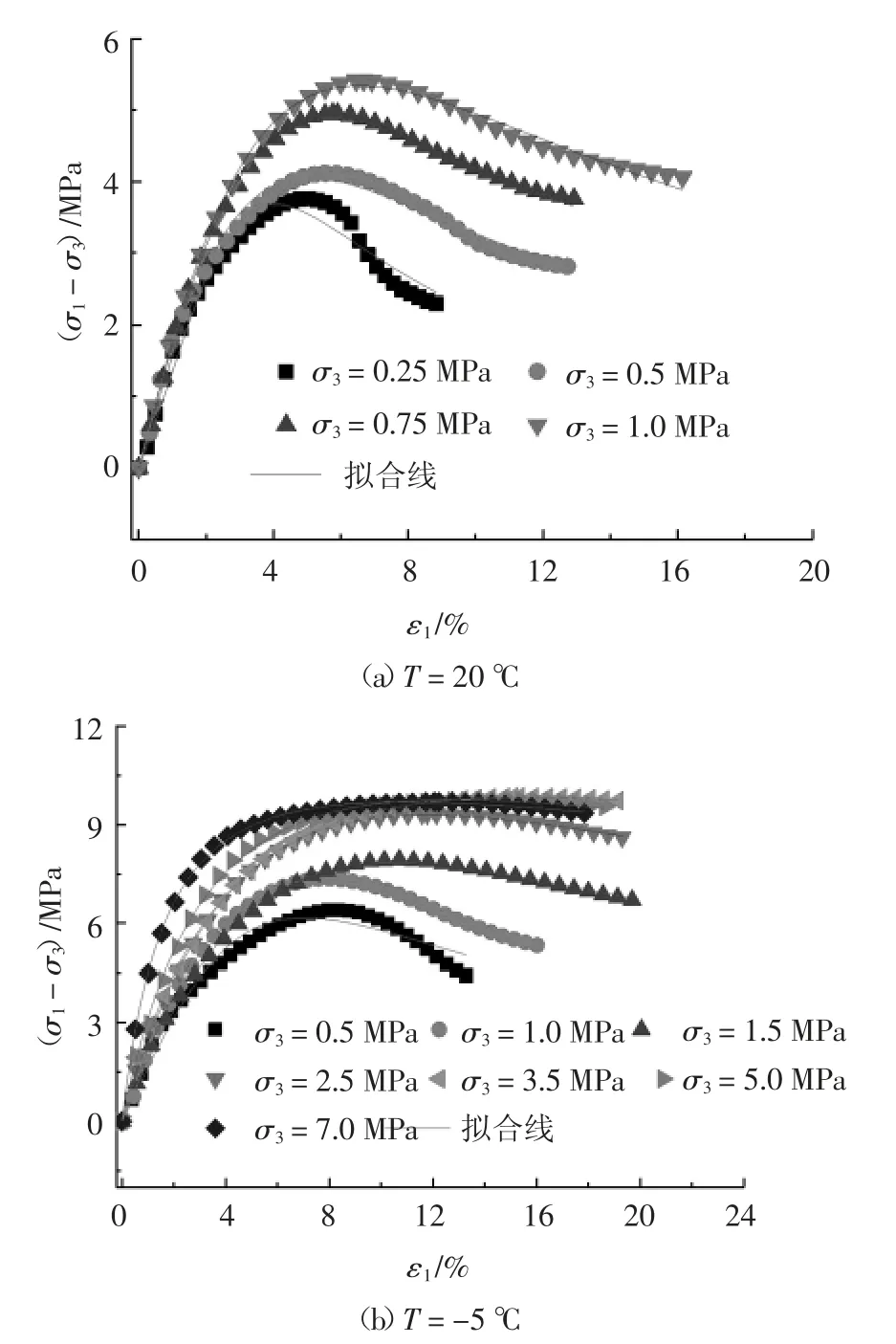
图2 水泥土偏应力-轴向应变曲线Fig.2 Curves of deviatoric stress-axial strain of cement-reinforced soil

室温状态下施加的围压较小时，偏应力-应变曲线峰后脆性明显，随着围压增大，应力峰值附近的塑性变形也增大.峰值应变与围压的关系如图3 所示.

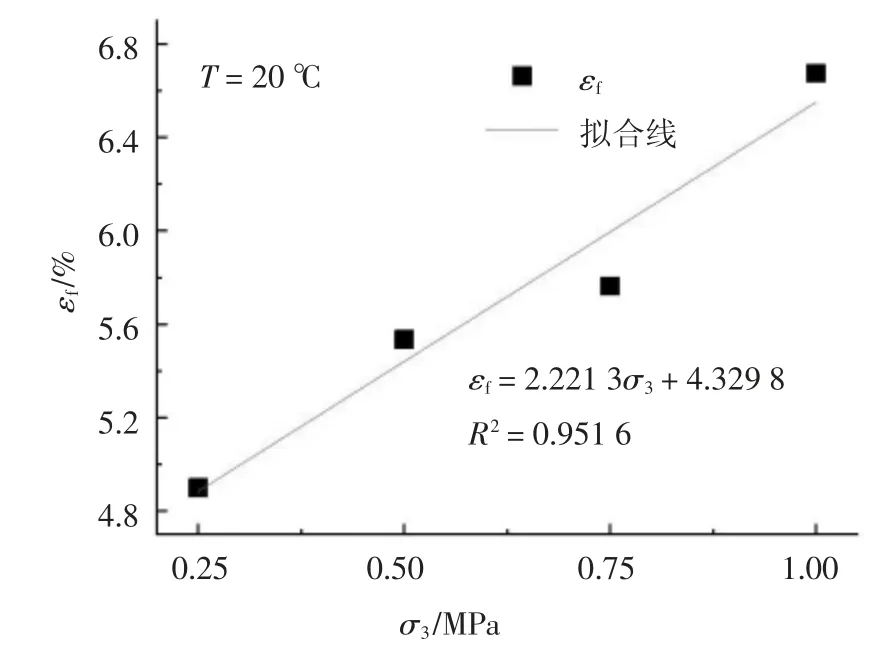
图3 峰值应变和围压的关系Fig.3 Relation between peak strain and confining pressure

由图3 可知，峰值应变随围压的增大而增大，两者呈线性关系，可用式（2）表示，相关系数高达0.951 6.

2.2 初始切线模量E0 特征

三轴压缩过程中 dσ1=dσ2=0，根据式（1）可求得试验起始ε1=0 时的切线模量：

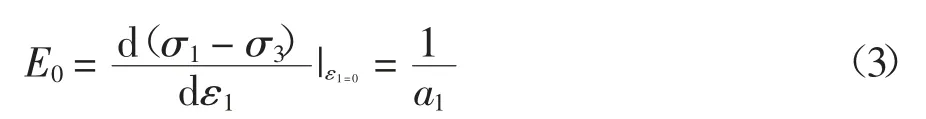
可知式（3）中参数a1代表试验初始切线模量E0的倒数.室温和冻结状态下水泥土的E0与围压关系如图4 所示.

图4 初始切线模量与围压的关系Fig.4 Relationship between initial tangent modulus and confining pressure

从图4 可知室温和冻结状态下初始切线模量E0均随围压增大而增大，但变化形式不同.室温状态下初始切线模量E0随围压增大而增大，但增大趋势迅速变缓，可借鉴围压对岩石杨氏模量影响公式来描述二者之间关系[22]，拟合公式示于图4 中.认为水泥土试样内部含若干裂隙缺陷，轴向荷载增加时，裂隙之间可能发生有摩擦的滑移，也可能不发生滑移.当围压较大时发生滑移的裂隙较少，表现出初始切线模量E0随围压增大而增大.较小的围压就可使大部分裂隙缺陷受到约束而不发生滑移，随着围压继续增大，受约束的裂隙缺陷数目增加较小，表现为初始切线模量E0增大趋势变缓.冻结状态下初始切线模量E0同样随围压增大而增大，开始时增长趋势较缓，随着围压增大，增长趋势也越来越大.冻结水泥土强度较大，较小围压难以使其压密，其内部受约束的裂隙缺陷数目较少，表现为初始切线模量E0随围压增大缓慢增大.冻结水泥土在较大围压作用下变得更加致密，虽然较大围压会使冻结水泥土内部冰晶压融而产生新的裂隙缺陷，但其内部越来越多的裂隙缺陷受到约束，表现为初始切线模量E0随围压增大迅速增大.冻结状态下水泥土E0与围压的关系可用指数函数表示，拟合公式如图4（b）所示.

2.3 强度特征

本文强度取值说明，当图2 中水泥土偏应力-轴向应变曲线呈应变软化时取峰值偏应力作为极限强度；当偏应力-应变曲线呈应变硬化时，取轴向应变为15%对应的偏应力值作为极限强度.

室温和冻结状态水泥土强度随围压的变化规律如图5 所示.从图5 中可以看出，室温状态下水泥土强度随围压增加而增大；冻结状态水泥土强度随围压增加呈现出先增大后略微减小的趋势.围压小于3.5 MPa 时，冻结状态水泥土强度随围压增加迅速增大；围压大于3.5 MPa 时，强度基本不变甚至略有减小.

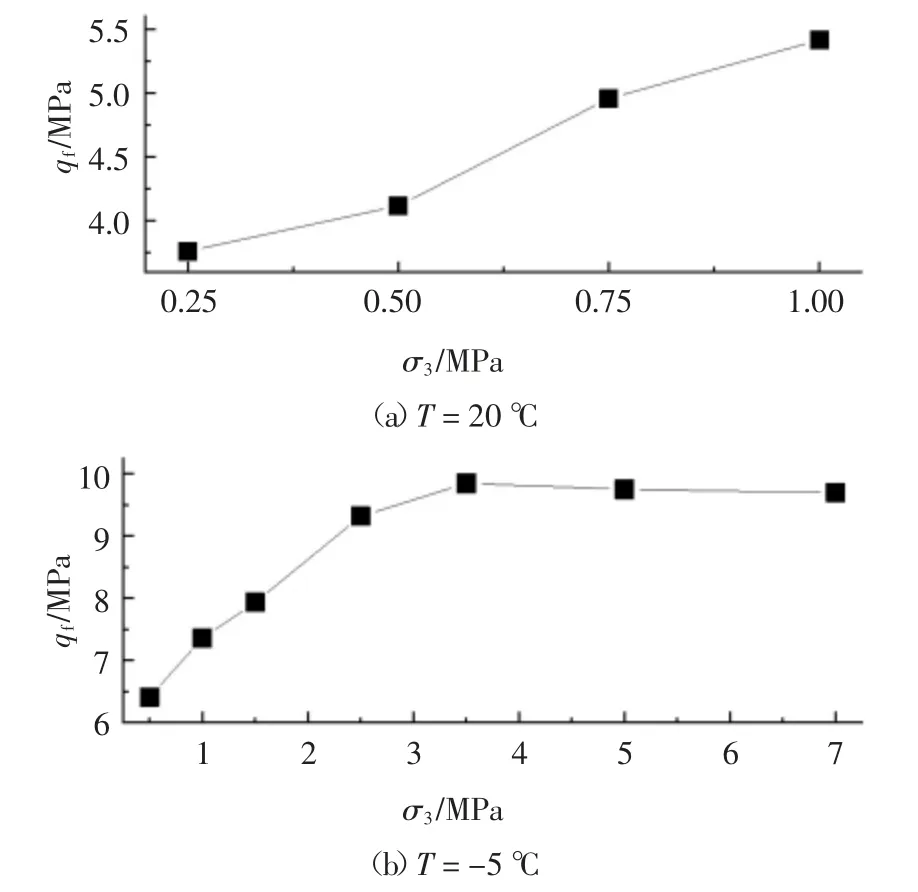
图5 强度随围压的变化规律Fig.5 The variation of strength with confining pressure

线性的Mohr-Coulomb 强度准则与非线性的Hoek-Brown 强度准则在描述岩土材料破坏时的最大轴向应力σ1max与围压σ3关系中广泛应用，二者表达式分别如下：

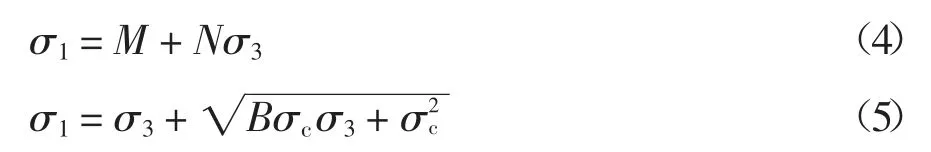
式中：M 和N 为强度准则参数，分别为M=2ccos φ/（1-sin φ），N=（1+sin φ）/（1-sin φ）=tan2（45°+φ/2）；σc为水泥土单轴抗压强度，室温和冻结状态下分别为2.22、5.83 MPa；B 为材料拟合参数.

室温和冻结状态下水泥土试样的最大轴向应力σ1max与围压 σ3的关系如图6 所示.随着围压 σ3增大，室温和冻结状态下水泥土的最大轴向应力σ1max逐渐增大.利用Coulomb 准则进行回归，回归参数及相关系数示于图6 中.可得室温状态下黏聚力c 为0.641 MPa，内摩擦角 φ 为 37.08°，破坏面的法向与试样轴向的夹角为63.54°；冻结状态下黏聚力c 为2.70 MPa，内摩擦角12.79°，破坏面的法向与试样轴向的夹角为51.40°.室温和冻结状态下水泥土试样的最大轴向应力σ1max与围压σ3的关系虽然均可用线性的Mohr-Coulomb 强度准则回归且得到的相关系数较高，但是当σ1=0 时外推得到的抗拉强度σt分别为0.64、4.32 MPa，与实际情况差别较大.

图6 第一主应力和第三主应力关系的拟合曲线Fig.6 The fitting curve of the first principle stress vs.the third principle stress

此外，大量有关冻土强度的研究表明，围压较小时，由于受到围压的作用，冻土三轴剪切过程中其内部裂隙和孔洞发展受到限制，颗粒间的胶结作用得到一定程度的增强，最终表现为围压对冻土强度的强化作用；随着围压的进一步增大，冻土内的冰晶发生压融，使未冻水含量增大，颗粒间胶结强度减小，最终表现为高围压对冻土强度的弱化作用.从图2中冻结状态水泥土偏应力-轴向应变曲线可知，当围压大于等于3.5 MPa 时，随着围压进一步增大，最大偏应力几乎不变.从图6 可以看出，非线性的Hoek-Brown 强度准则在描述室温状态下水泥土的第一主应力σ1和第三主应力σ3关系时与Mohr-Coulomb强度准则相比相关系数更高，在拉伸区得到更符合实际的抗拉强度σt.但是其同样无法反映出高围压对冻土强度的弱化效应，因此对Hoek-Brown 强度准则进行如下形式的修正：

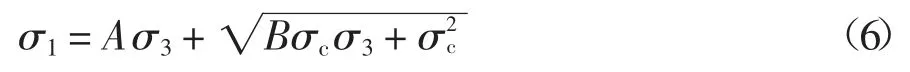
式中：A 为拟合参数，其值为负，能够反映出高围压下冻结水泥土中冰晶发生压融，强度随围压的增大而降低.

利用修正的Hoek-Brown 强度准则对冻结状态下水泥土试样的最大轴向应力σ1max与围压σ3的关系进行回归，结果如图6 所示，相关系数较高且在拉伸区得到的抗拉强度σt为0.69 MPa.采用巴西劈裂法对冻结状态下水泥土抗拉强度σt进行测试，结果如图7 所示，试验测得的抗拉强度为0.65 MPa.对比可知利用修正的Hoek-Brown 强度准则计算得到的拉伸区抗拉强度σt与试验实测值比较接近.

图7 基于巴西劈裂测得的抗拉强度Fig.7 Tensile strength measured based on Brazilian splitting

讨论：由冻土强度随围压变化的临界围压的概念可知，当σ3趋近于临界围压σcr时，图5 中曲线斜率 q′为 0，如图8 所示，有：

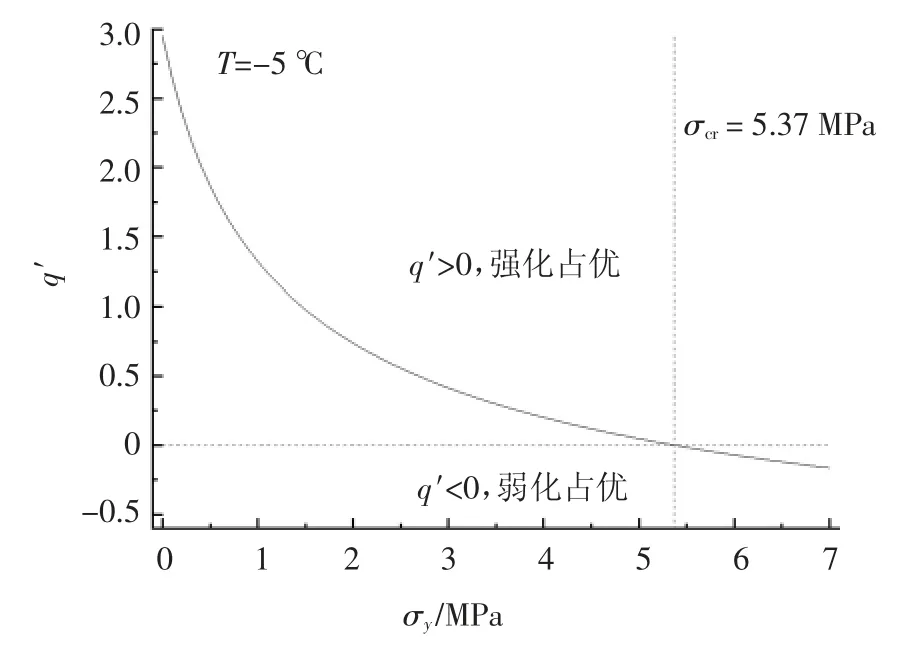
图8 q′与围压关系Fig.8 Relationship between q′and confining pressure

求解公式（7）可得到：

可以看出根据改进的Hoek-Brown 强度准则确定的临界围压σcr和水泥土单轴抗压强度值σc=5.83 MPa 接近.基本能够反映图5 中强度随围压的变化规律，围压7.0 MPa 时极限偏应力qf减小.

为考察本文提出的适用于冻结状态的水泥土的改进Hoek-Brown 强度准则的适用性，将其与文献[21]中式（9）所示的强度准则进行比较.

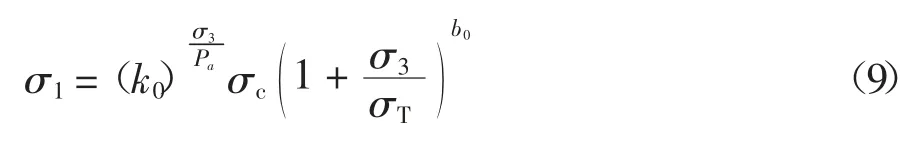
式中：Pa为标准大气压，取 0.101 33 MPa；σc和 σT分别为冻结水泥土的单轴抗压强度和抗拉强度；k0和b0均为试验参数，对于温度为-5 ℃、掺量为15%的冻结水泥土，σc和 σT分别取 5.83 MPa、0.69 MPa.

通过以下方式将试验数据代入上述两种强度准则来确定强度准则中包含的参数：考虑所有8 组试验数据确定强度准则中的参数，然后依次去掉最小围压时试验数据，采用剩余试验数据确定强度准则中的参数，得到两种强度准则中参数及相关系数如表1 所示，分别统计两种强度准则中参数平均值和最大相对误差.

从表1 中可以看出，两种强度准则中参数变化较小，相关系数较高.从表1 中还可以看出根据不同围压组数下试验数据确定的改进Hoek-Brown 强度准则参数计算出的临界围压σcr变化很小，最大相对误差仅为1.288%.

根据Mohr-Coulomb 强度理论可知，冻结水泥土试样破坏时剪切面上的正应力σ 和剪应力τ 有如下关系：

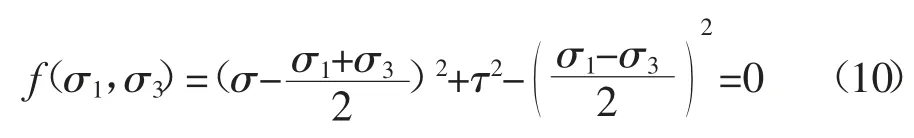
将式（6）改写为如下形式：

根据包络线理论可得：

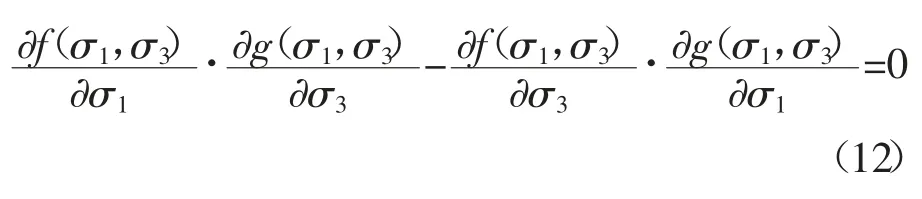
对式（10）和式（11）微分得：

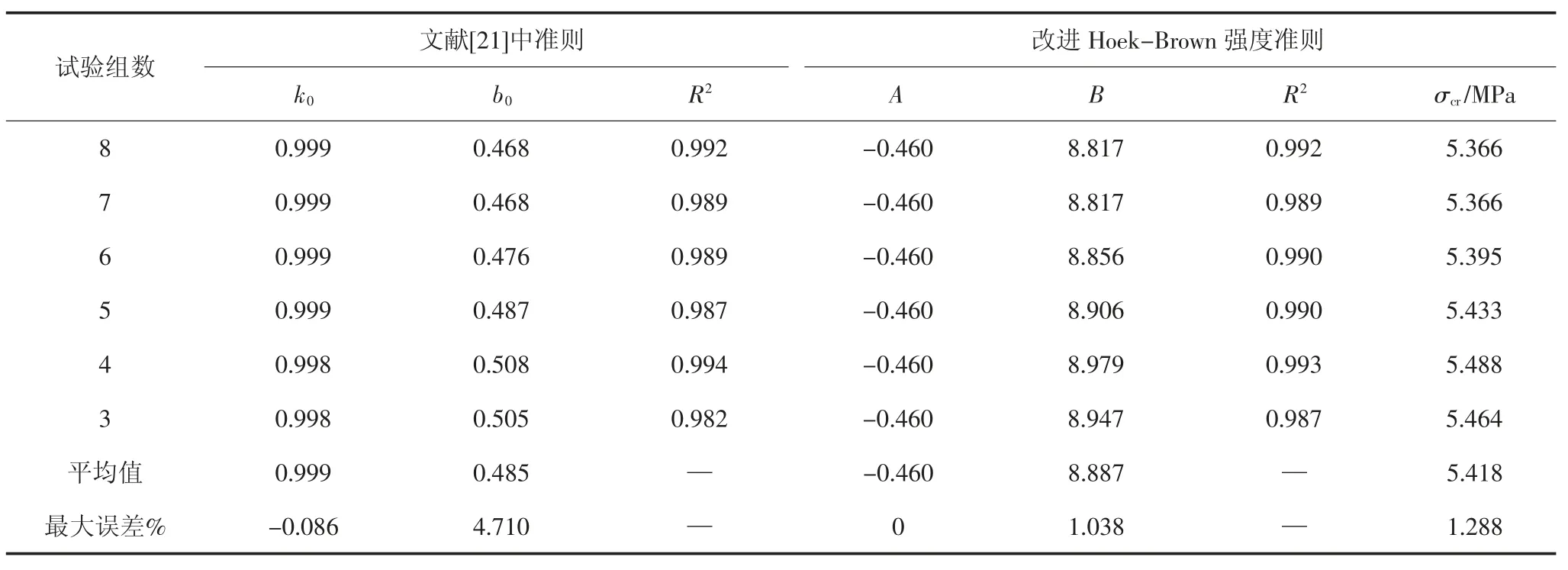
表1 两种强度准则参数Tab.1 Parameters of two strength criterion

将式（13）代入式（12）得到正应力 σ 和剪应力τ的表达式如（14）所示：

式（14）即为冻结水泥土采用破坏面上正应力σ和剪应力τ 表达的非线性强度准则，由此绘制出不同围压下应力圆及基于改进的Hoek-Brown 强度包线如图9 所示.

图9 冻结水泥土不同围压下应力圆及强度包线Fig.9 Stress circle and strength envelope curve under different confining pressure of frozen cement-reinforced soil

3 基于Hoek-Brown 强度准则的损伤本构模型

假设室温和冻结状态下水泥土微元体强度的分布规律服从双参数的Weibull 分布[16-23]，基于前文非线性的Hoek-Brown 强度准则和修正的Hoek-Brown强度准则描述室温和冻结状态下水泥土微元破损时有效第一主应力和有效第三主应力的关系，通过水泥土三轴试验数据确定模型参数值，建立复杂受力状态下水泥土损伤本构模型.

3.1 模型建立

根据Lemaitre 提出的应变等价性假说及其推广，可得荷载作用下水泥土损伤本构关系[24]，即：

式中：σ 为表观应力；E 为水泥土弹性模量；即基准弹性模量；D 为荷载作用下的损伤变量；ε 为应变.

D 可从宏观角度定义为荷载作用下已破损单元数目与总单元数目之比[25]，即：

式中：Nf为荷载作用下已破损单元数目；Nt为总单元数目.

考虑到水泥土试样内部初始缺陷的非均质性和随机性，采用双参数的Weibull 分布描述水泥土微元体强度F 的分布规律.进而可认为荷载作用引起的损伤变量D 也服从该统计分布，表达式如下[26]：

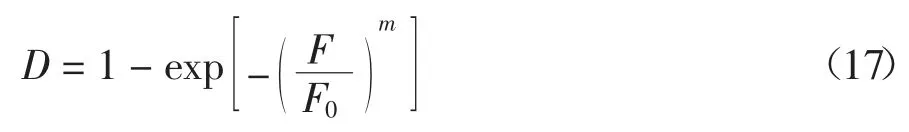
式中：m、F0分别为形状参数和尺度参数.

采用Hoek-Brown 强度准则和修正的Hoek-Brown 强度准则分别描述室温状态和冻结状态下水泥土微元强度，表达式如下：

式中：σ*为与表观应力相对应的有效应力，二者之间换算关系如下[23]：

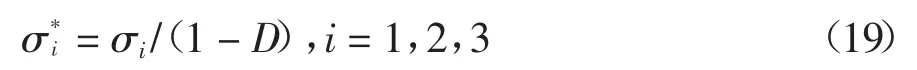
常规三轴试验可以得到表观应力σ1，σ2=σ3，轴向应变ε1，根据虎克定律有：

根据公式（15）（17）（20）可得：

室温和冻结状态下水泥土微元强度用表观应力分别表示为：

根据公式（17）（21）得到如下表达式：

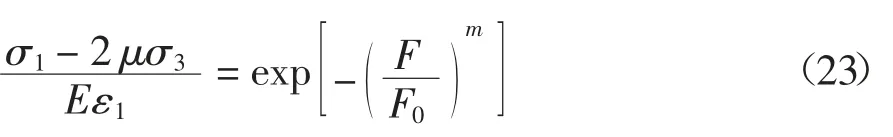
对式（23）两边取对数，移项，再取对数可得[23]：

通过线性拟合三轴试验数据可以得到m 和W，进而可得：

3.2 模型参数确定

利用上述方法，根据室温和冻结状态水泥土三轴压缩试验数据对损伤本构模型中参数进行确定，模型参数m 和F0如表2 所示.

已有关于模型参数m 和F0物理意义的研究表明[23]：参数m 反映了材料的脆性及延性特征，m 越大，材料脆性特征越明显，峰值应变越小；参数F0反映了材料的强度特征，F0越大，材料强度越大，抵抗破坏的能力越强.从表2 可以看出，拟合得到的参数m 和F0随围压的变化而变化.参照文献[27-28]的方法，利用模型参数m 和F0随围压的变化规律对模型参数进行修正，以冻结状态下数据为例，模型参数m和F0修正结果如式（27）所示，模型参数与围压关系如图10 所示.

表2 三轴试验结果拟合参数Tab.2 The fitting parameters of triaxial test results

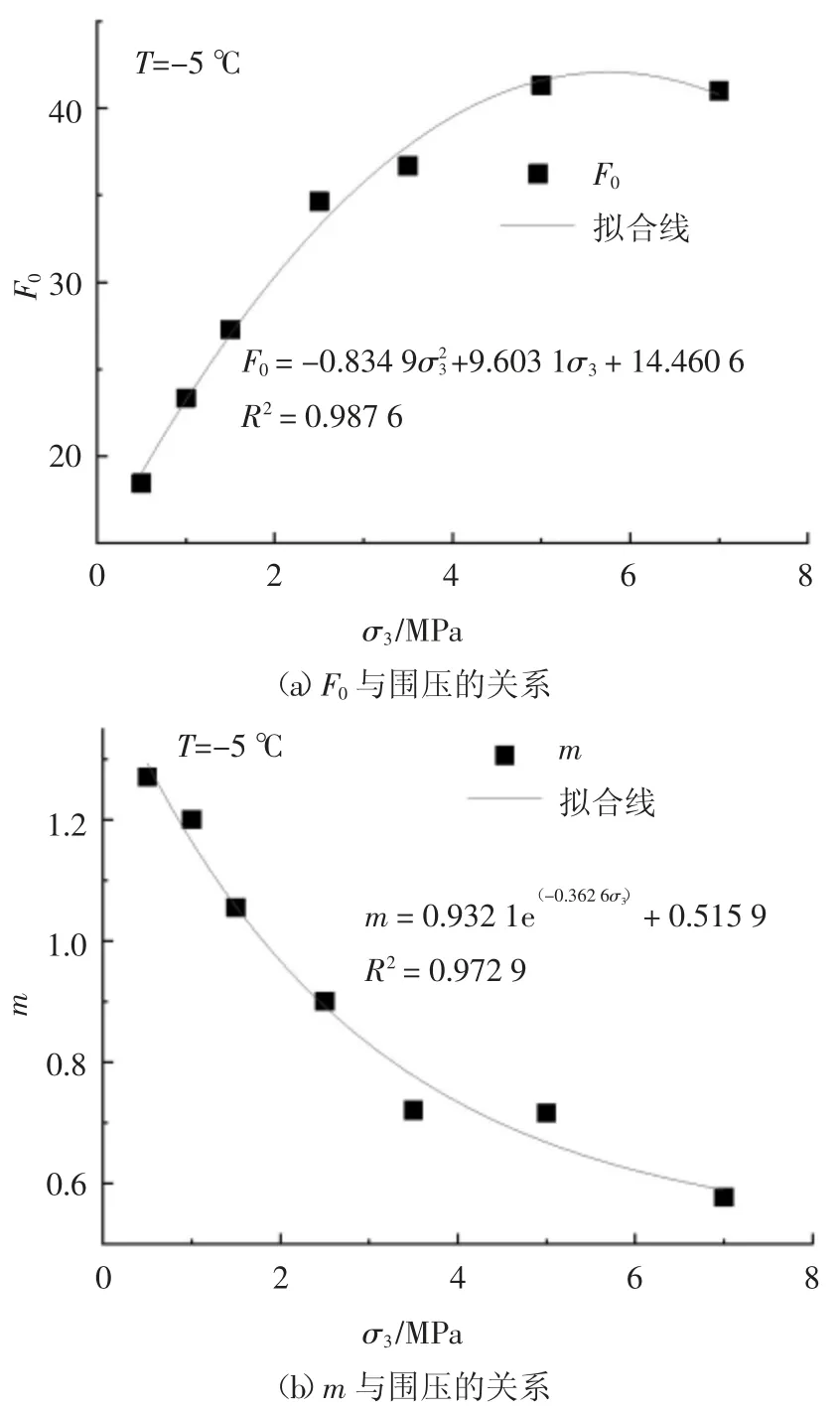
图10 Weibull 分布参数与围压的关系Fig.10 Relationships between confining pressures and distribution parameters of Weibull function

从图10 可看出，尺度参数F0随围压增加呈现抛物线变化趋势.当σ3趋近于临界围压σcr= 5.37 MPa 附近时，F0达到峰值；随着围压继续增加，F0值减小.形状参数m 随围压增加呈指数规律衰减，说明随着围压增加冻结水泥土脆性减弱.

至此即可得到室温和冻结状态下水泥土的考虑围压对模型参数影响的统计损伤本构模型.

式中：F0和 m 由式（27）给出，F 由式（22）得到.

3.3 损伤本构模型曲线与试验曲线比较

根据所建立的损伤本构模型得到不同围压下应力-应变曲线与室温和冻结状态下水泥土三轴压缩试验应力-应变曲线进行比较，如图11 所示.

从图11 中可以看出，所建立的统计损伤本构模型能较好地预测室温和冻结状态下水泥土应力-应变曲线.该模型能够反映出冻结状态水泥土低围压下的应变软化现象（围压小于3.5 MPa，图11（b）所示）与高围压下的应变硬化现象（围压大于等于3.5 MPa，图11（c）所示），同时能够反映水泥土强度随围压变化的特征.

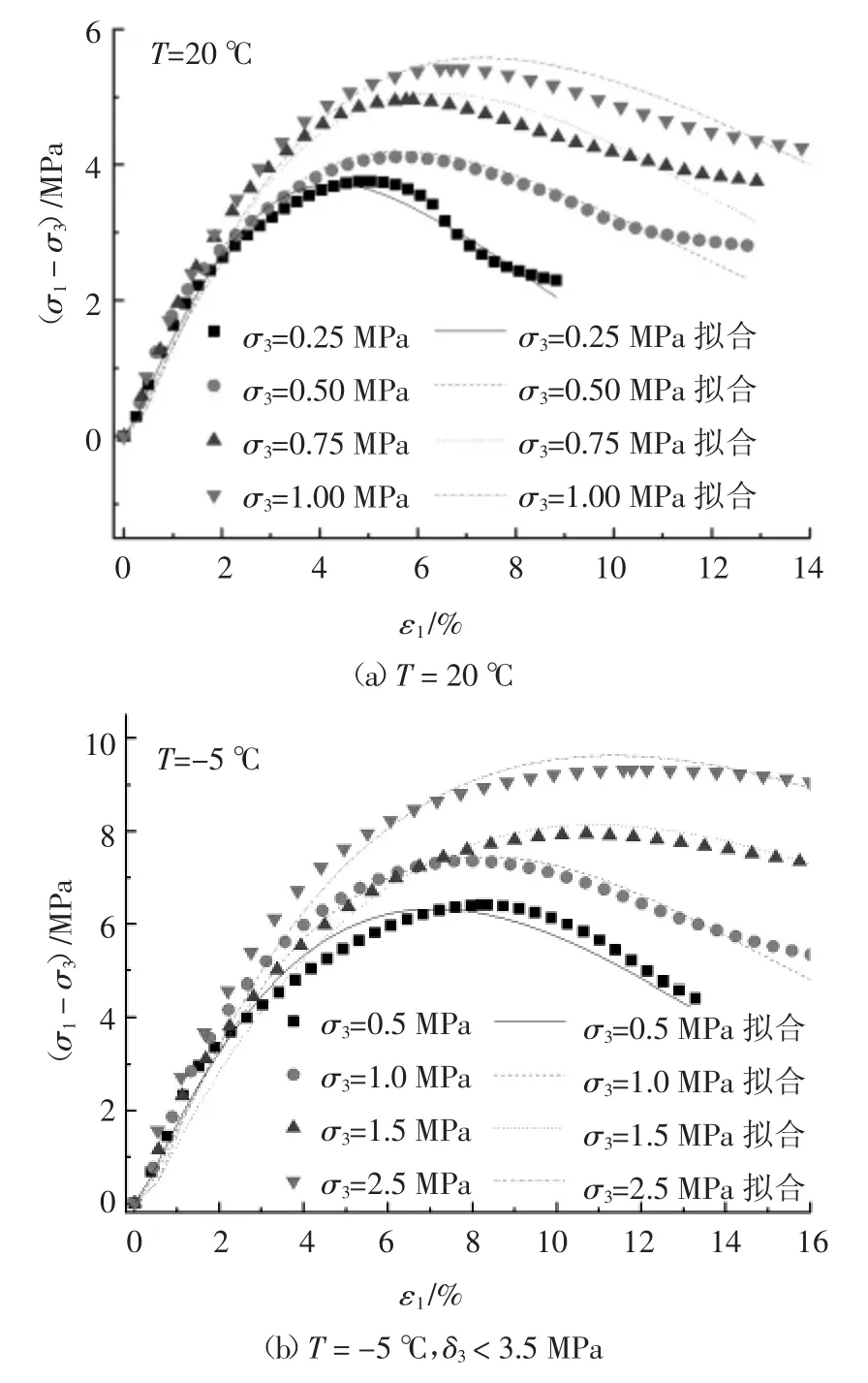
图11 试验曲线与模型曲线比较Fig.11 Comparison between experimental and theoretical curves

3.4 损伤变量演化特性

根据公式（17）（22）（27）可得室温和冻结状态荷载作用下水泥土损伤变量D，图12 为室温和冻结状态水泥土在不同围压下的损伤变量D 演化曲线.

从图12（a）中可看出，室温状态时不同围压下损伤变量D 与轴向应变关系曲线形状相似，均随轴向应变增加呈“S”型单调递增.围压越大，达到相同应变时损伤变量D 越小，表现出较高围压下水泥土损伤劣化过程变缓，损伤程度减小.这是由于较高围压限制了变形过程中试样内部缺陷的发展，使其力学性质得到改善.结合图11（a）还可看出，在偏应力-应变曲线线弹性阶段，损伤变量D 增长缓慢，线弹性阶段结束时，不同围压下损伤变量D 较小且差别不大.在偏应力-应变曲线由线弹性阶段过渡到塑性阶段，不同围压下损伤变量D 迅速增加且差别逐渐增大.

冻结状态时水泥土在不同围压下的损伤变量D同样表现出随轴向应变增加而增加，但围压对损伤变量曲线形状影响较大.当围压较小（0.5 ～2.5 MPa）时，围压对损伤变量D 的影响机制与室温状态类似，结合偏应力-应变曲线可知此时围压对冻结水泥土的强化作用占优势.随着围压进一步增大，相同轴向应变时损伤变量D 表现出随围压增大而增大，即高围压使得损伤加剧.高围压下（如围压为7.0 MPa），损伤变量D 在轴向应变很小时就表现出急剧的增长趋势.轴向应变为 1%时，围压为 1.0、5.0、7.0 MPa 时损伤变量分别为0.08、0.27、0.41.说明高围压导致冻结水泥土试样内部冰晶压融，水泥石颗粒间胶结强度减小，此时围压对冻结水泥土的弱化作用占优势.

图12 不同围压下损伤变量与轴向应变关系曲线Fig.12 Curves of damage variables and axial strain under different confining pressures

4 结 论

本文考虑水泥土材料非均匀性和随机性的特点，基于连续介质损伤力学理论，结合Hoek-Brown强度准则及其修正形式，建立了室温和冻结状态下水泥土统计损伤本构方程，得到的主要结论如下：

1）室温状态时水泥土在不同围压下的应力-应变曲线均表现出应变软化现象.当围压小于3.5 MPa时，冻结状态下水泥土的应力-应变曲线表现为应变软化现象，围压大于等于3.5 MPa 时表现为应变硬化现象.

2）非线性的Hoek-Brown 强度准则在描述室温和冻结状态下水泥土极限第一主应力和第三主应力关系时具有较高的精度，通过对Hoek-Brown 强度准则的形式进行修正，其能够描述低围压对冻结水泥土强度的强化作用和高围压的弱化作用.

3）基于Hoek-Brown 强度准则及其修正形式建立的损伤本构模型能够较好地描述室温和冻结状态下水泥土应力-应变曲线，且能够反映出冻结状态水泥土低围压下的应变软化现象与高围压下的应变硬化现象.冻结状态下得到的尺度参数F0随围压增大呈现出先增加后减小的二次曲线变化规律，与冻结水泥土强度随围压变化规律吻合.

4）室温状态时不同围压下损伤变量D 均随轴向应变增加呈“S”型单调递增.围压越大，相同应变时损伤变量D 越小，表现出较高围压下水泥土损伤劣化程度减小.冻结状态下低围压抑制水泥土损伤劣化程度；高围压使其损伤劣化程度增加.