第一主族元素原子光谱精细结构强度比值计算

王陆君瑜 谭志阳 陈康宁 吴 平 陈 森

(北京科技大学 1材料科学与工程学院 2数理学院； 3土木与资源工程学院；4自然科学基础实验中心，北京 100083)

氢原子及碱金属原子光谱是近代物理实验教学中的一个重要实验内容，有助于学生对原子光谱精细结构和量子缺的理解。该类原子光谱具有不同的线系，精细结构的强度具有不同的比值，对于一个特定的线系而言，其比值接近一个定值。在实验教学中，往往主要关心谱线对应的波长，却很少关注谱线的强度比[1]，而谱线的强度比反映了从高能级到低能级的跃迁速率，能级的布居数等信息，因此光谱线的强度也是一个值得关注的点。查阅相关文献发现，前人虽然研究过氢原子及碱金属原子各线系的谱线强度比，但是对上下能级均存在由于精细结构而产生能级分裂的情况，无法进行直接计算，而需要将上能级或者下能级进行简并，考虑为一个能级再进行计算，且在计算过程中还要引入下能级的布居数[2-4]。而按照爱因斯坦辐射理论，光谱线的强度为Imn=NmAmnhνmn，其中Nm是上能级的原子数目，Amn是自发辐射系数，νmn是谱线频率，在计算过程中我们只应该出现上能级的原子数，而不应出现下能级的原子数。因此本文提出了一种更为精确的对氢原子及碱金属原子光谱不同线系精细结构强度比值的计算方法，直接从量子跃迁的角度出发，在电偶极辐射近似下，对自发跃迁几率进行计算，进而求出谱线强度的比值。

1 跃迁几率计算

由爱因斯坦的受激辐射理论，有：

(1)

式中A21为爱因斯坦自发辐射系数，代表单位时间原子从上一能级到下一能级的自发辐射概率；B21为受激辐射系数。取能级非简并的情况，则有B12=B21，B12为受激吸收系数。在室温下，可见光波段，受激辐射强度与自发辐射的比值为：

(2)

所以受激辐射、受激吸收系数与自发辐射系数相比均可以忽略。

由量子力学理论可知，从Ψnljmj跃迁到Ψn′l′j′m′j的自发辐射系数[5]为：

(3)

式中ωkk′为辐射光子的角频率，其中rkk′满足rkk′=〈Ψnljmj|r|Ψn′l′j′m′j〉。

由公式(3)可以看出对于两个固定能级，角频率为确定的值，主要计算矩阵元rkk′即可。径向部分对于从nl能级跃迁到n′l′是相同的，意味着只要上下能级的主量子数和角量子数固定，径向部分就是定值。而对于氢原子及碱金属原子，价电子的能量本征态可选为守恒量完全集(H,l2,j2,jz) 的共同本征态，即Ψnljmj=R(r)φljmj，其中φljmj满足[5]：

(4)

所以矩阵元可以写作：

(5)

下面分类讨论：

1.1 对于l′=l+1的情况

1.1.1φA→φA型

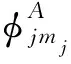
(6)

1.1.2φB→φB型

(7)

此时相当于φA→φA型中阶数降一。

1.1.3φA→φB型

(8)

1.1.4φB→φA型

不符合选择定则，此时是禁止跃迁的。

1.2 对于l′=l-1的情况

1.2.1φA→φA型

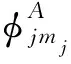
(9)

1.2.2φB→φB型

(10)

此时相当于φA→φA型中阶数降一。

1.2.3φA→φB型

不满足选择定则，此时是禁止跃迁的。

1.2.4φB→φA型

(11)

最终结果都表明对于上一能级，无论mj取值如何都不影响最终计算结果，在实验仪器无法区分这些简并态时，我们假定每一种态出现的概率都相等，相当于计算结果乘上1/g，g为该能级的简并度，最后再求和，得到的结果仍和未考虑简并的结果一致。

根据以上推导结果，就可以对钠原子光谱的精细结构谱线强度进行定量计算。

2 精细结构谱线强度比值计算结果

光谱线的强度为：

Imn=NmAmnhνmn

(12)

在系统与外界处于分布热平衡时，原子的布居数服从玻尔兹曼：Nm=gme-hν/kT,gm为该能级的简并度。

2.1 主线系

(13)

2.2 锐线系

相当于从n′s→np跃迁，n′=n+1,n+2,n+3,…，n′s→np3/2相当于l→l+1,φA→φA，相应的谱线强度令为I1；而n′s→np1/2相当于l→l+1,φA→φB，相应的谱线强度令为I2。因为第一主族元素原子p能级二重态的能量间隔的量级是10-3eV远小于kT，由式(6)、式(8)、式(12)得：

(14)

2.3 漫线系

(15)

2.4 基线系

(16)

3 与已有理论及实验结果的比对

3.1 氢原子

以Hα(Dα) 谱线为例，其严格理论计算结果如表1所示[2]。

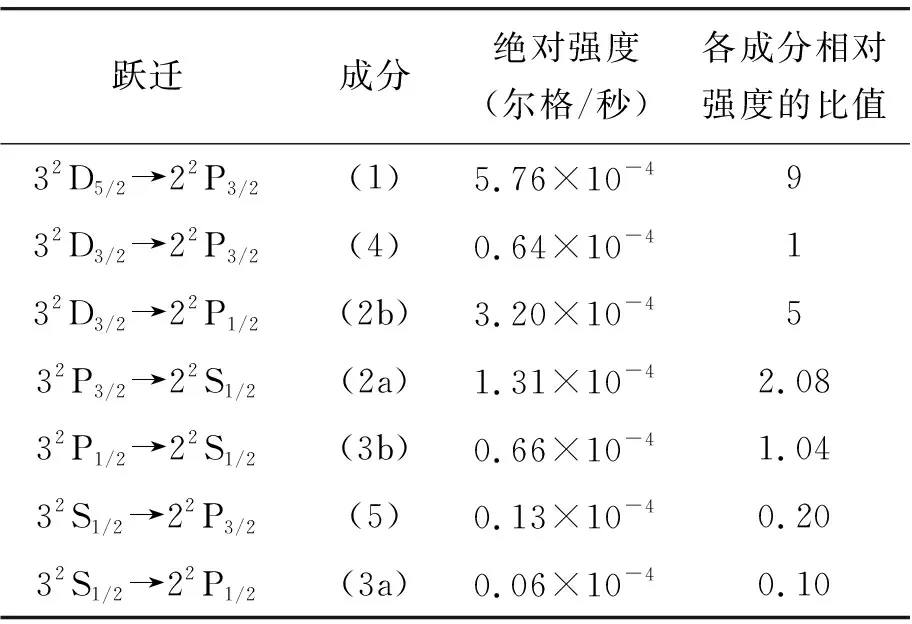
表1 Hα(Dα)精细结构成分的强度[2]

由表1可得，对于Hα(Dα)原子，3p→2s谱线精细结构强度比值为2∶1，3s→2p谱线精细结构强度比值为2∶1，3d→2p谱线精细结构强度比值为9∶1∶5，这与本文给出的计算方法所得结果相符。

3.2 碱金属原子

目前较为普遍的计算谱线双重结构强度的定量规律为强度和定则，而本文的计算结果与强度和定则的计算结果完全一致[6]。在利用强度和定则求解时，必须联立方程，同时求出两能级之间所有精细结构谱线强度比值。而本文提供方法可以求出碱金属原子两能级之间任意两条精细结构谱线强度比值，不必同时解出所有精细结构谱线的强度比值，对具有复杂精细结构的谱线具有应用和推广价值。

实际实验得到的碱金属元素原子的主线系和漫线系精细结构谱线强度比值分别如表2和表3所示[6]。

表2 碱金属主线系的谱线强度[6]

由表2可得，对于主线系，第一条线与观察结果符合得很好，理论值为2∶1，而较高序数的谱线则有所偏离或不再符合，这种现象可以解释为自旋-轨道相互作用的结果[6]。由表3可得，对于漫线系，理论计算结果与观察结果符合得很好，均约为9∶1∶5。 虽然理论预期的强度不总是与观测相符合，但是这个近似的理论强度比在辨认一些还未被分析的光谱中是非常有用的。

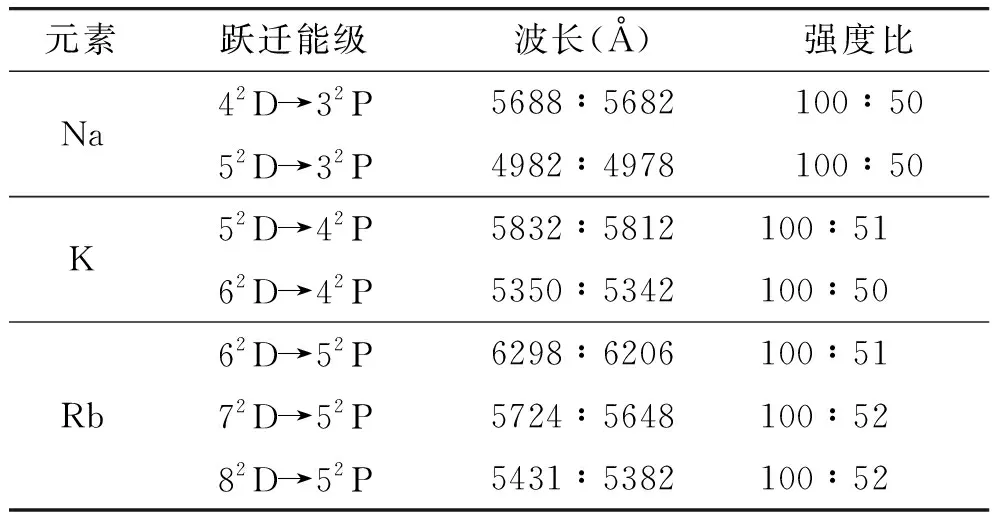
表3 碱金属漫线系的谱线强度[6]

4 结论

主线系的精细结构谱线强度计算比值为2∶1，锐线系的精细结构谱线强度为2∶1，漫线系的精细结构谱线强度比值为9∶1∶5，基线系的精细结构谱线强度比值为20∶1∶14，与已有理论结果完全吻合[2]，该计算方法避免了引入更多的近似假设而导致的物理逻辑上的不严谨，物理模型更清晰，逻辑性更强，更具有普适性，有利于学生对原子光谱线精细结构的深入理解。