一类平面几何问题与静电场镜像法的联系

王伟良 许绍群 邓文基 徐 湛 张宏浩 姚道新

(1中山大学物理学院，广东 广州 510275； 2广东实验中学，广东 广州 510055； 3华南理工大学物理系，广东 广州 510641； 4清华大学物理系，北京 100084)

物理学是自然科学的基础，在中学和大学阶段的物理教育对培养青年学生的科学素养和理性思维具有重要作用，但由于物理课程本身具有一定的难度，部分中学生在学习过程中可能会产生畏惧心理，学习效果往往不尽如人意。如果我们在中学开始的教学和训练中有意识地培养学生们对物理乃至自然科学的学习兴趣，调动他们的学习积极性，就可以取得事半功倍的效果。本文的其中一位作者在中学数理化教育实践中巧妙地将一道平面几何题与大学物理电磁学中的镜像法联系起来，开阔了同学们的视野，激发同学们对物理的好奇心，也有助于加深他们对中学物理的理解。本文的问题及涉及的知识点可作为中学与大学物理教学衔接的一个典型范例。

1 一道中学训练题

图1 当点P在圆弧上运动时，求的最小值

2 一种函数求解方法

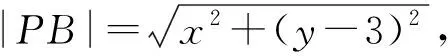
3 巧妙的几何解法

4 大学物理静电学中的镜像法

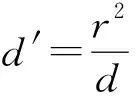
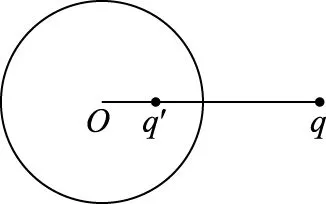
图2 导体球外的电荷q及其镜像电荷q′

5 设计更一般的几何问题

图3 点A、B和它们的对偶点A′、B′

6 讨论和思考

当然，如果脱离了球对称性去讨论一般形状(例如椭球、立方体)的导体，一般就不能再使用这种简单的镜像法了，这是这种对偶点方法的一个局限。球对称性是大自然中一种十分常见而又十分特别的对称性，只有在这种对称性下才存在球内外的对偶点。

本文例子表明，在中学数理化与大学物理的一些知识点之间可以有相通之处。如果我们在日常教学实践中能够像这样将应试教育中的某些枯燥题目与一些有物理背景的有趣问题联系起来，把中学数理化与大学物理的知识点衔接起来，也许就可以激发学生们学习物理、学习科学的兴趣，从而吸引更多优秀的青年学生选择将来投身于科学研究。

致谢：作者感谢王青教授、潘逸文副教授和胡剑博士的有益讨论。