激光雷达复材型面测量精度分析方法
2020-07-25潘鑫张俐何凯
潘鑫,张俐,*,何凯
(1.北京航空航天大学 机械工程及自动化学院,北京100083;2.航空工业成都飞机工业(集团)有限责任公司 复材厂,成都610092)
复合材料(以下简称复材)因其高比强度、低密度、易于实现设计制造一体化等优点在航空、航天、汽车、电子电气等领域的得到了广泛应用[1]。与钣金成型及机加工零件相比,复材零件在制造过程中一旦固化成型后,其型面的变形误差将无法再次进行校正,只能从设计角度进行结构优化,因此需要准确地获取脱模后复材零件的型面信息。传统检测通过塞尺等手段测量零件局部区域的变形量,随着数字化检测技术与测量设备的发展,高精度测量仪器逐渐用于复材零件的型面检测领域[2-3]。将数字化测量得到的点云数据与零件的理论制造模型进行对比,能够实现产品复杂曲面的变形分析,测量结果将作为成型模具修正与优化的参考依据[4-5]。
目前,复材零件的数字化检测所采用的设备包括激光跟踪仪、激光雷达、摄影扫描仪等。文献[6]介绍了激光跟踪仪在复材零件检测中的应用,包括模具检测与安装检测等方面;文献[7]运用激光雷达对复材零件的制造过程进行检测,研究模具、筋条的变化对零件成型过程产生的影响;文献[8]采用摄影扫描测量技术对复材零件外形进行检测,再通过逆向建模对模具进行工艺补偿。随着被测对象测量精度要求的不断提高,数字化检测仪器本身的测量误差对最终测量结果产生的影响已不可忽略,型面的测量精度将会对变形量结果的计算产生很大的影响。
根据ISO计量联合委员会指南(2012)的基本概念和相关术语定义[9],测量结果可以采用“测量值+不确定度”的形式进行表示。因此,针对采用激光雷达实现复材零件数字化检测的方式,本文研究了一种基于激光雷达回波信号信噪比(SNR)的复材型面测量精度分析方法。利用激光雷达回波信号的信噪比,确定精度修正因子κ,计算测量工程的实测不确定度,量化测量误差对点云结果产生的影响,最终能够准确地计算出零件变形量的大小。该方法还考虑了待测距离、入射角和材料属性对测量结果产生的影响。
1 激光雷达测量精度分析
激光雷达的表面点测量模式属于非接触测量。雷达的发射光学系统将发出2束光线:测量光与参考光。参考光进入固定长度的标准光纤进行直接传输,测量光经过发射光学系统入射到待测型面后返回,随后混频器将接收到的反射激光与射向雷达内部标准光纤的激光进行混频,计算出2束激光的频率差与时间差,最终得到激光测量系统与被测点的绝对距离[10],测距原理如图1所示,PS为回波信号强度,PQ为光学系统的量子极限功率,PW为系统发射信号强度。因此,激光雷达的测量信息主要包含在系统所接收的激光雷达回波信号中,测量的准确度取决于信号的强弱。
信噪比是系统接收到信号与噪声的比值,可作为信号质量与强度的衡量指标。激光雷达信噪比则定义为待测目标的回波信号强度与雷达接收光学系统所能探测到最小信号强度之间的比值[11]。在雷达的测量过程中,系统提供回波信号信噪比的监视窗口,如图2所示。因此,在测量过程中可以对测点信噪比的峰值数据进行采集,并将其记作该点的质量因子(Quality),作为测点质量优劣的衡量指标。
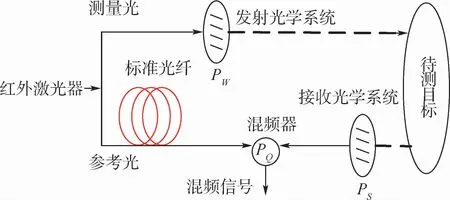
图1 激光雷达测距原理Fig.1 Principle of lidar ranging
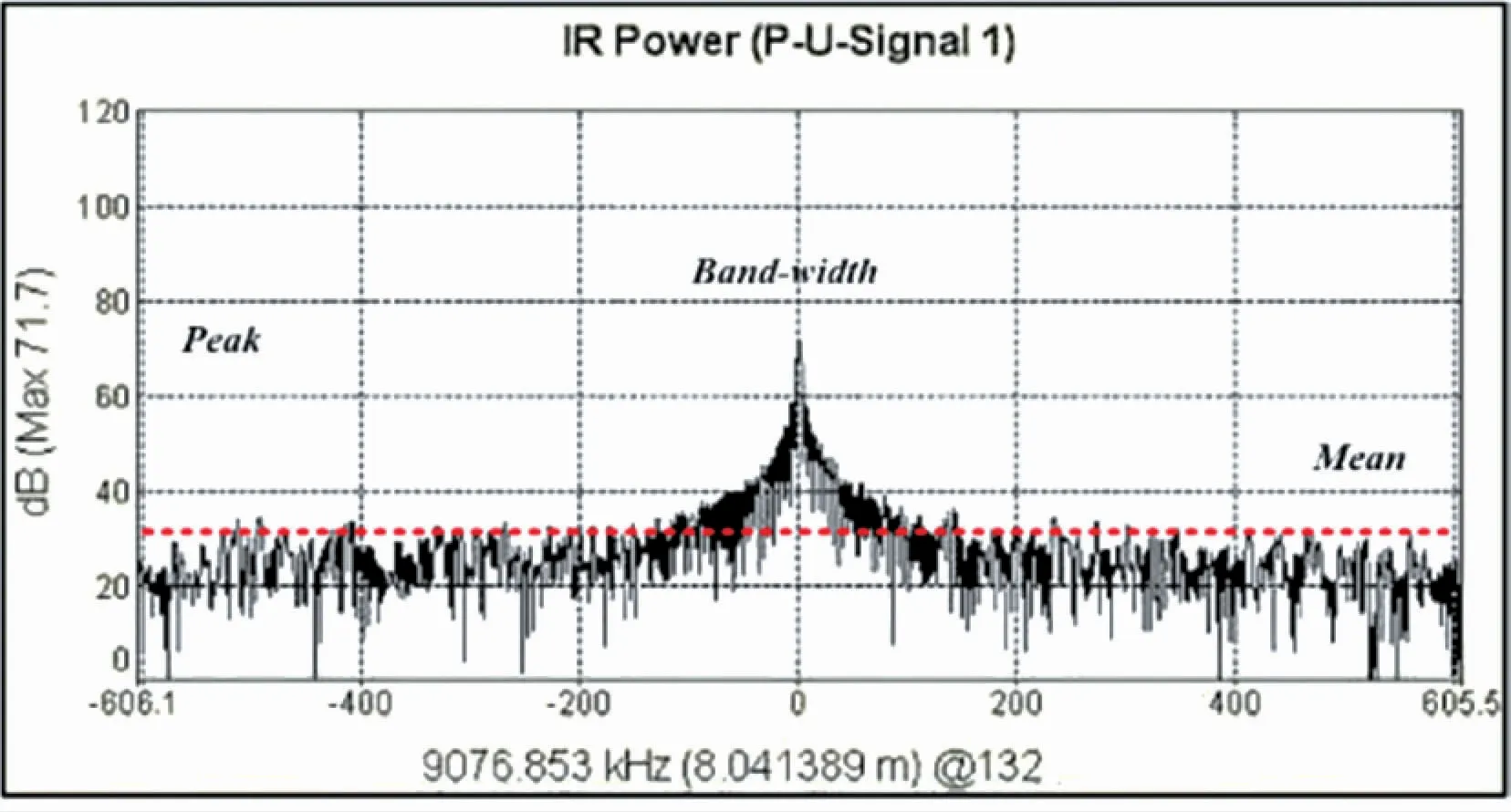
图2 激光雷达信噪比监视窗口Fig.2 Lidar’s SNR monitoring window
本文基于激光雷达测量过程中回波信号信噪比的变化规律,研究其测量精度分析方法。首先依据测量工艺确定零件的放置状态与激光雷达的站位,然后采用工具球获取测量空间内各区域的信噪比强度,建立仪器标准不确定度与信噪比强度的联系。利用相同距离条件下工具球与复材回波信号信噪比之间的比值,确定精度修正因子κ,最终实现不同区域型面点云数据测量精度的修正,消除测量偏差对变形量检测结果的影响。该方法工作内容主要包括3个部分:
1)确定零件的放置状态、雷达测量站位,评估测量空间的覆盖尺寸。利用雷达标准工具球获取特定距离下的信噪比强度,将仪器标准不确定度与信噪比数值对应起来。
2)利用激光雷达对待测零件执行型面检测,测量过程中需要观察记录复材零件目标信噪比随待测距离的变化情况,确定精度修正因子κ。
3)结合修正因子κ,依据待测距离、入射角等信息对结果点云进行分区,修正型面检测结果的测量精度,分析复材零件成型后产生的变形量。
分析方法的具体操作流程如图3所示。
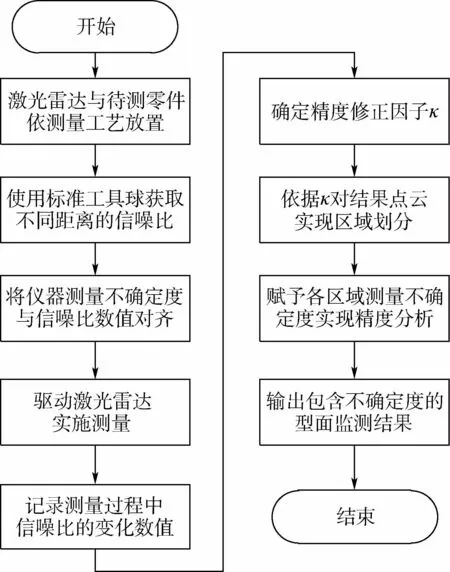
图3 精度分析流程图Fig.3 Flowchart of accuracy analysis
2 求解精度修正因子
2.1 激光雷达信噪比求解
激光雷达系统的回波信号强度受待测型面散射特性、入射角、待测距离等因素的影响,因此,计算回波能量的信噪比需要明确这些因素对其产生的影响。其中,可采用激光雷达散射截面(LRCS)作为待测型面散射特性的量度[12]。
探测型面的激光雷达散射截面表征的是入射到目标表面激光的散射能力,以面积为计数单位[13]。LRCS与激光波长、目标材料与结构、辐射测量与标定原理、激光探测原理、背景与大气环境等因素相关,其数值可以利用双向反射分布函数BRDF通过积分求得,用目标反射率ρ表示[14]。通常情况下,球体目标的激光雷达散射截面表示为

式中:r为球体目标半径;ρd为目标反射率。
结合激光雷达的系统参数,通过计算推导,将系统所接收的回波信号强度PS表示为
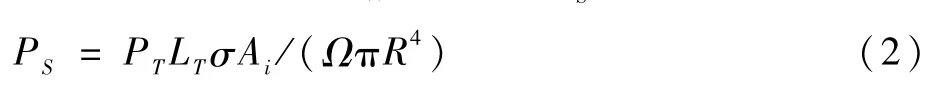
式中:PT为雷达的发射光学系统功率;LT为测量工程的整体损耗系数,包括大气损耗、光能传输损耗及系统效率损耗等;σ为待测型面激光雷达的散射截面;Ai为接收系统透镜的面积;Ω为发射系统立体角;R为待测距离。
采用光学系统的量子极限功率表示激光雷达的最小探测功率PQ。由于雷达信号的探测方式属于激光外差探测模式,因此系统所能探测的信号强度可以通过外差等效功率表示,记作

式中:B为测量信号带宽;(NEP)Het为外差等效功率[11]。因此信噪比定义式为
2.2 不同测量状态下的修正因子
激光雷达的仪器测量精度通常采用不确定度进行描述。校准证书所提供的描述字段是基于合作目标的仪器标准不确定度,而型面检测属于无合作目标的非接触式测量,测量不确定度将与实验室校准精度存在差异。通过引入精度修正因子κ,结合材料属性、入射角、待测距离等信息,研究信噪比强度的变化规律,可以实现对仪器测量不确定度的修正与实际测量的精度分析。
结合式(4),当测量目标为工具球时,测量空间内各向反射强度均匀,其雷达散射截面表示为σ0=4πρ0R20cosφ[15],ρ0和R0分别为工具球的反射率和待测距离,φ为工具球入射角,此时的工具球信噪比SNRTB记为

当测量目标为复材型面时,测量光束直径小于目标尺寸,属于漫反射扩展目标,散射截面可表示为σ=πρθ2R2[15],ρ和R分别为复材型面的反射率和待测距离,θ为复材型面入射角,此时的复材型面信噪比SNRSP记为

通过κ修正仪器不确定度进而获得实际测量结果的不确定度。从式(7)可以看出,κ的量化需要考虑待测距离与入射角变化产生的影响。图4表示复材检测时待测零件的2种放置状态,根据激光雷达的站位,利用系统的水平角φ与俯仰角ω表示复材测量光的入射角θ,其光路示意如图4所示。
根据图4(a)推导出平视状态下入射角θ满足:


图4 测量时激光雷达的站位与光路示意图Fig.4 Schematic diagram of position and optical path of lidar during measurement
将2组角度关系式代入式(7)中,得出复材零件俯视状态与平视状态时的精度修正因子κ:
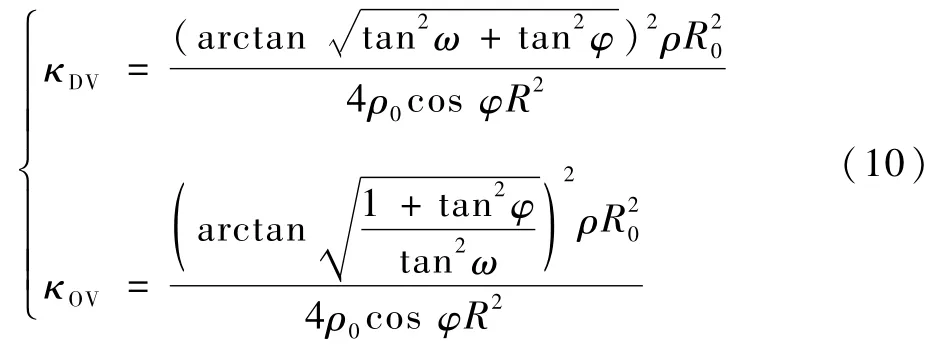
通常状态下,激光雷达平视时水平角φ∈[-π/3,π/3],俯仰角ω∈[-π/4,π/4];雷达俯视时水平角φ∈[-π/3,π/3],俯仰角ω∈[-π/4,0)。将除角度之外的所有参数视为常量,绘制κ随入射角θ变化的网格图,如图5所示。再结合待测距离R的信息,从图中提取对应网格节点上的数据,最终得到精度修正因子κ。
通过精度修正因子κ对测量结果点云实施分区,结合待测距离与入射角信息的差异,求解每个区域所对应κ的值。κ能够将仪器不确定度修正为实测不确定度,并将其赋给测量结果,实现复材型面测量精度的分析。精度分区的示意图如图6所示。
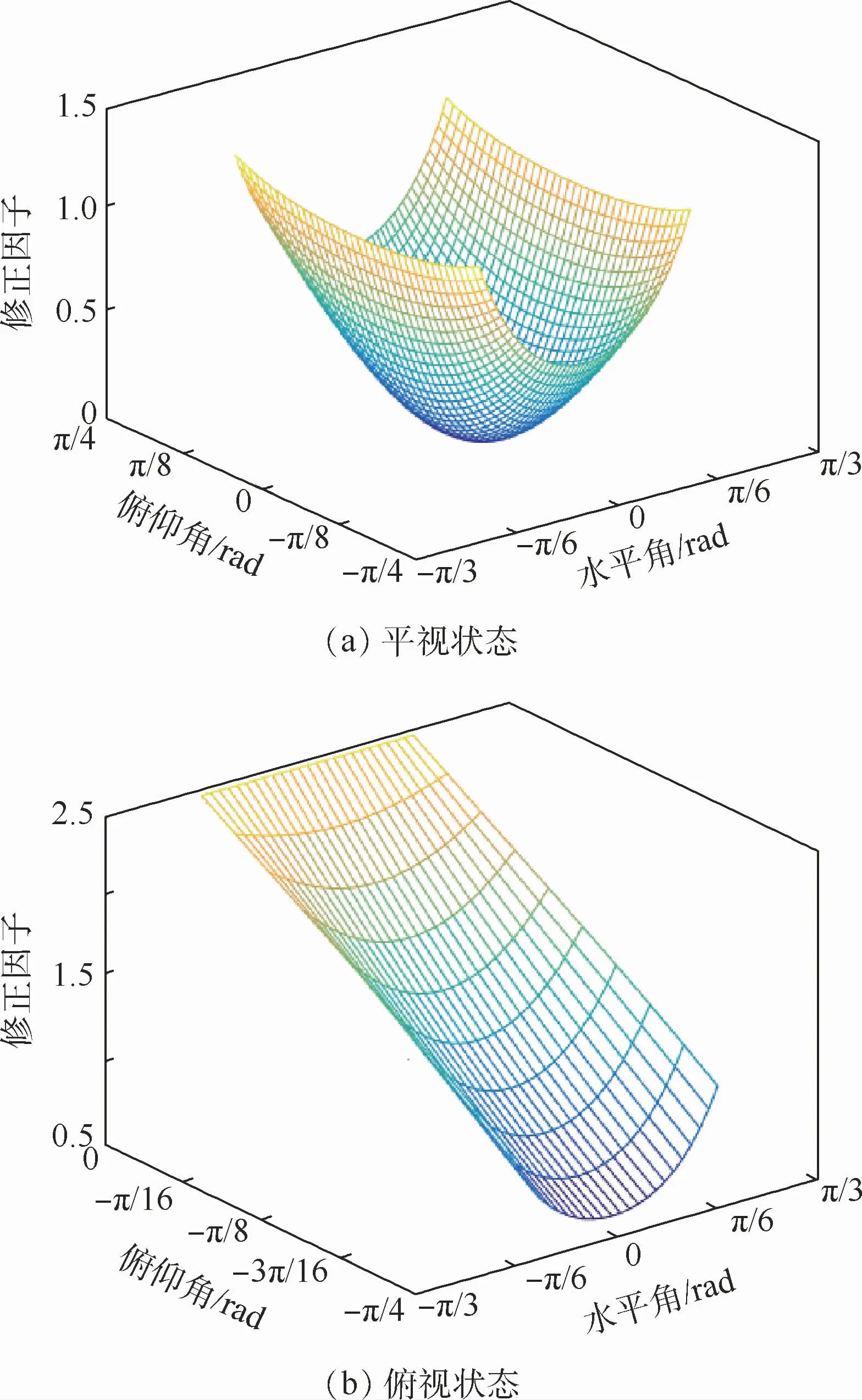
图5 2种状态κ随入射角θ变化网格图Fig.5 Grid diagram ofκas a function of incident angleθin two states
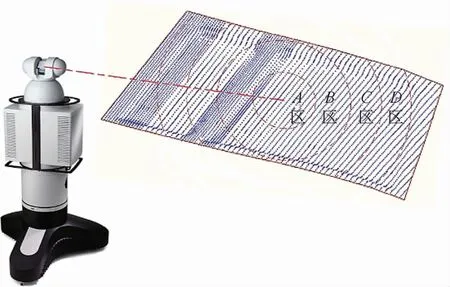
图6 测量结果点云依修正因子κ分区Fig.6 Partition ofmeasurement result point-cloudaccording to correction factorκ
3 信噪比变化分析实验
通过第2节的分析可以得出,激光雷达测量时的信号强度受多种因素影响,在同一测量工程中,PT、LT、Ai、B、(NEP)Het等因素基本不变,实测信噪比的数值大小主要与待测距离、目标反射率等因素有关。因此,本节通过实验分析待测距离、表面特性、材料属性对SNR数值产生的影响,研究信噪比的变化规律。
实验采用的激光雷达型号为Nikon MV330,工作空间范围1~30m,水平角测量范围±180°,俯仰角测量范围±45°,标准测距精度(2σ)为10μm+2.5μm/m;实验现场为恒温净化间,温度为(24±0.5)℃,湿度为60% ±2.5%。
3.1 信噪比随待测距离变化分析实验
选择标准工具球作为待测型面,在1~10 m的测量空间内进行单点测量实验。调整雷达的俯仰角与水平角数值为0°,每隔0.5m采集1组数据,记录激光雷达测量窗口的信号峰值与监视窗口的信号均值,绘制出的折线图如图7所示,CF为置信度。
从图中可以看出,随着待测距离的增加测量信号的信噪比逐渐降低,接收光学系统所探测到的信号强度减弱;近端的降低速率快,远端的降低速率漫,符合实验预期结果。

图7 工具球测量信号强度随待测距离变化曲线Fig.7 Variation ofmeasurement signal strength of tooling ball with measurement distance
3.2 信噪比随表面处理方式变化分析实验
通过实验分析同属性材料,采用不同类型的表面处理对测量特性产生的影响。此实验选择不锈钢304与黑化处理的45#材料2种同类型的金属材料,数据采集方式与3.1节实验相同,记录激光雷达测量窗口的信号峰值,绘制出的折线图如图8所示。
从图8中可以看出,同类型待测对象经过不同类型的表面处理后,接收光学系统所探测的信号强度将会产生变化,产生SNR变化梯度。因此,复材测量实验中对于需要喷涂显影剂辅助测量的区域,应当单独划分区域进行精度分析。
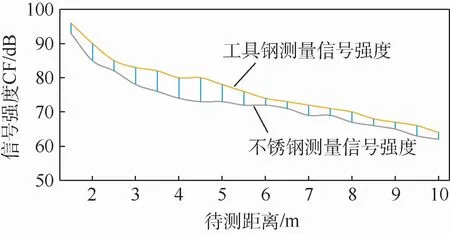
图8 不同表面处理目标测量信号强度随待测距离变化曲线Fig.8 Variation ofmeasurement signal strength of target with different types of surface treatment with measurement distance
3.3 信噪比随材料属性变化分析实验
通过实验分析激光雷达测量不同类型材料时,信号强度的变化情况。此实验选取标准工具球,摄影测量荧光标志、金属材料和复材4种类型的待测型面,数据采集方式与3.1节实验相同,记录激光雷达测量窗口的信号峰值,绘制出的折线图如图9所示。
从图9中可以看出,测量信号强度受待测对象材料的影响,工具球与荧光标志等参考元素的回波信号强度高,复材与金属材料的回波信号强度低,且工具球与复材的SNR对距离变化敏感,表明复材型面检测过程中同一零件不同区域的点云测量精度存在差异,验证了分区修正方法的合理性。
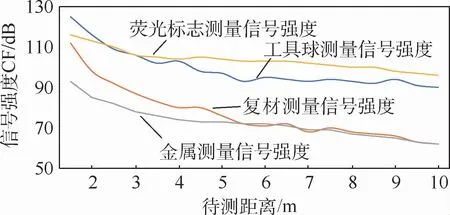
图9 不同材料目标测量信号强度随待测距离变化曲线Fig.9 Variation ofmeasurement signal strength of different materials of targetwith measurement distance
4 精度修正实例
以某大尺寸复材型面作为精度分析的实例,验证方法的可行性。测量所采用激光雷达的型号为Nikon MV330,测量空间尺寸12m×3m×2m,零件的测量许可误差在±0.5mm范围内。依据图3的示意流程完成测量精度分析。
1)零件水平放置在桁架上,激光雷达放置在待测型面的窄端,采用单站位完成测量任务。
2)使用标准工具球每隔1m获取一次信噪比数值,将信噪比数值与仪器的测量不确定度相对应,部分数据如表1所示。
3)驱动激光雷达实施测量,记录复材测量过程中信噪比的波动情况,如图10所示。
4)扫描完成后检验型面点云的完整性。根据需求针对缺失区域或变形量重点检测区域,使用显影剂进行表面处理,增强回波信号的强度。
5)结合待测距离与入射角确定精度修正因子。待测距离R在2~12m范围内变化,俯仰角在-40°~-6°范围内波动,水平角在±5°范围内波动,最终得到实际测量不确定度如表2所示;2σ条件下的包含区间长度在许可误差范围内,证明测量结果具有可靠性。
6)依据区域划分情况,将实测不确定度赋给结果点云,输出包含不确定度信息的型面检测结果,用于复材零件变形量的后续分析过程。截取零件部分点云结果及分区情况如图11所示。

表1 仪器不确定度与信噪比数值对应关系Tab le 1 Correspondence between instrum ent uncertainty and SNR
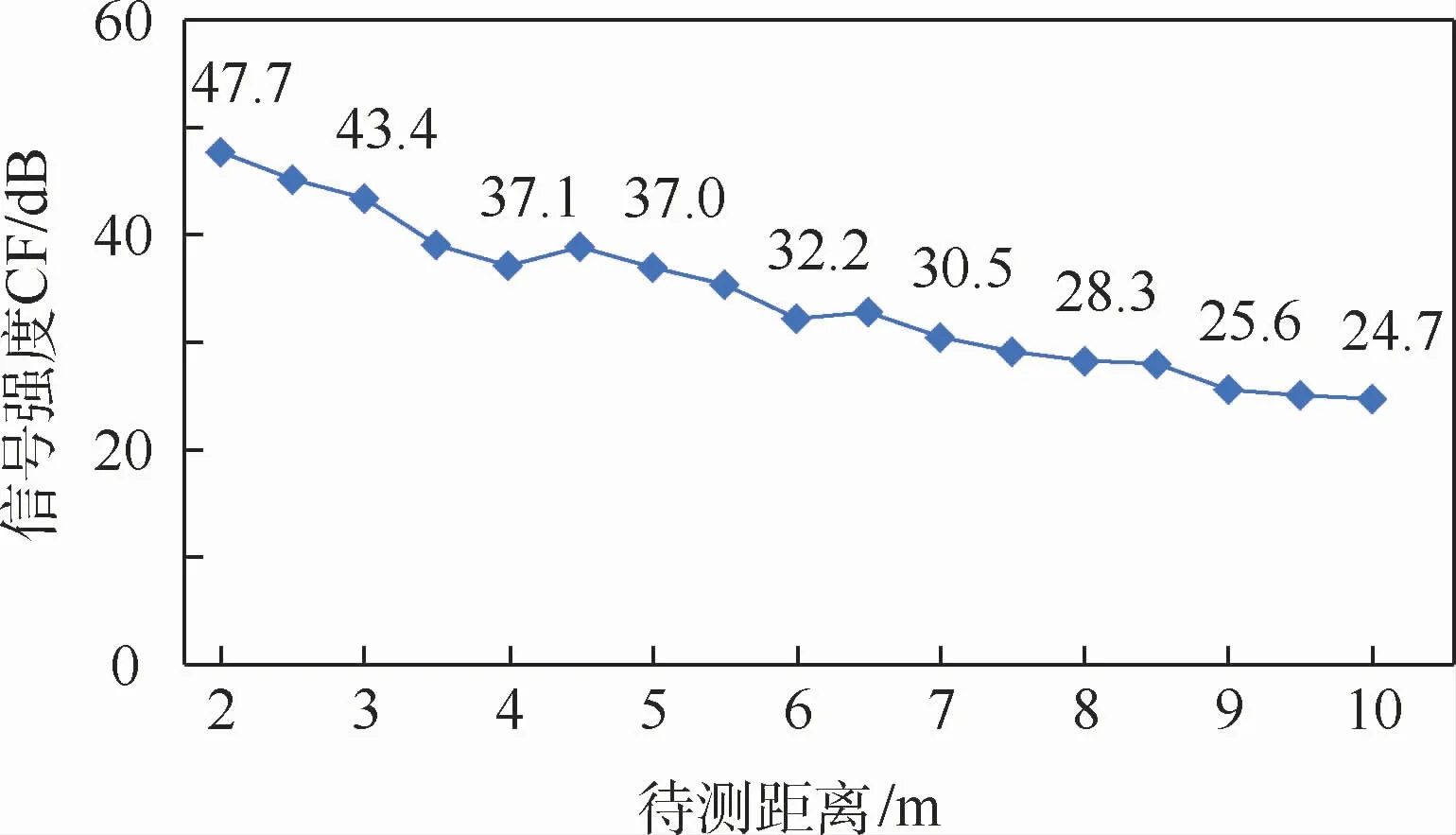
图10 复材实测过程中信噪比波动曲线Fig.10 SNR fluctuation curve during composite materialmeasurement process
7)变形量结果分析:将不确定度结果修正到点云坐标值中,消除测量误差对变形量计算产生的影响,如表3所示。计算结果的准确度得到了提高。
8)测量精度分析:采用线性模型不确定度合成公式计算点云的整体不确定度,作为测量工程的精度评价指标,各测点数据获取不相关。合成不确定度结果uc表示为
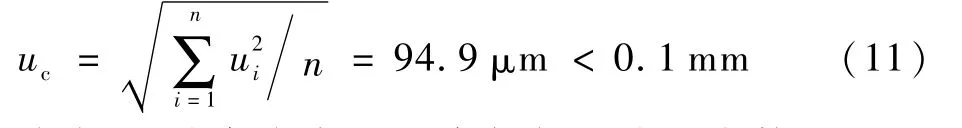
式中:ui为各点实测不确定度;n为测点数目。测量精度符合零件检测的许可要求。
最终,将型面点云与合成不确定度uc共同作为本案例的测量结果。相比于单纯输出点云进行变形量分析,利用信噪比对激光雷达测量结果的精度进行评价后,所输出的点云更符合复材零件实际的变形情况,能够提高逆向工程的准确度,减少设计修模的误差。
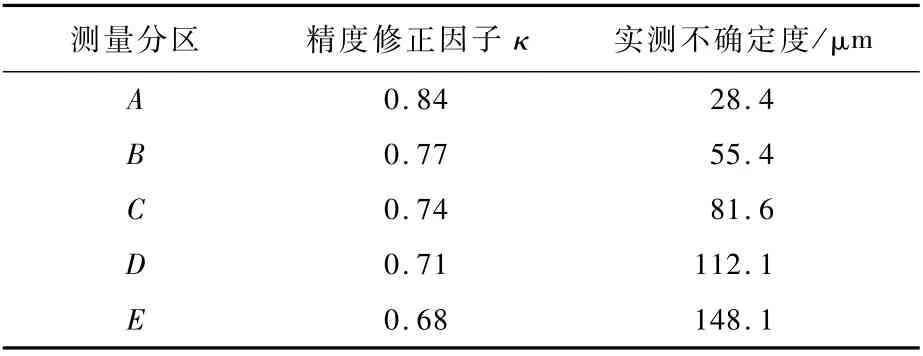
表2 精度修正因子与实测不确定度对应关系Table 2 Correspondence between accuracy correctionfactor and m easured uncertain ty

图11 测量结果点云与精度分区Fig.11 Point-cloud and precision partition of measurement results
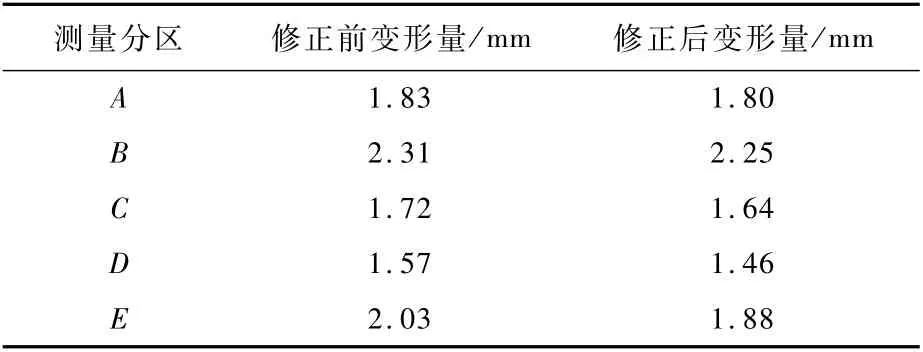
表3 精度修正前后各区域平均变形量结果Tab le 3 Average deform ation resu lts of each area before and after accuracy cor rection
5 结 论
本文针对采用激光雷达进行复材型面检测的方式,研究了一种基于回波信号信噪比的测量精度分析方法,通过实验与案例验证了方法的可行性,主要内容包括:
1)考虑测量误差对复材变形量计算产生的影响,采用不确定度量化结果点云精度,将测量结果表示为“测量值+不确定度”的形式。
2)采用LRCS表示复材型面散射特性,同时,引入待测距离和入射角变化对激光雷达测量精度产生的影响,推导出复材测量时激光雷达的回波信号信噪比。
3)研究回波信号信噪比随待测距离和入射角的变化规律,并利用不同待测型面的信噪比的比值设定精度修正因子κ,确定待测零件的实测不确定度。
4)根据回波信号信噪比的变化规律,对复材型面测量结果进行分区,针对不同区域逐一信息精度修正。
需要指出的是,为了提高精度修正因子的准确度,下一步需要考虑各因素耦合变化对其产生的影响,是后续工作中的研究重点。
