离散脉冲法测量水声材料反射系数

佟昊阳

（第七一五研究所，杭州，310023）

水声材料反射系数的测量一般在模拟自由场的消声水池和水声声管中进行。在消声水池中测量水声材料的反射系数，工作频率与样品的大小有关，样品的尺寸越大工作频率下限越低[1]。一般大面积样品的最大边长为1～2 m，采用宽带压缩脉冲法测量，测量样品反射系数的最低频率在2 kHz左右[2]。脉冲声管的工作频率与声管长度和内径有关，声管内径越小声管的截止频率越高，工作频率上限越高，而声管的长度越长可测量的声波波长越长，工作频率下限越低[3]。目前利用水声材料的行波管测量技术可以在内径为Φ208 mm、高度为5 m的声管中测量100 Hz～4 kHz频率范围内样品的反射系数[4]。

由于场地、设备以及样品尺寸的限制，对同一种样品的声性能测量往往需要制作多个样品。而且在水声材料研制过程中，若要对新材料的声性能进行测试，需要专门的设备和场地，测量用的时间也比较长，增加新材料的研发成本与研发周期。此外，在测量水中沙层、淤泥、油层等流体介质的反射系数时，声场的布置难度大，污染水池、声管的风险较高。为了减少水声材料的研发成本、缩短研发周期、降低测试装置的实验风险，本文介绍一种在狭小有限水域中能够较为精确的测量水声材料反射系数的离散脉冲法。

1 测量原理

离散脉冲法测量水声材料反射系数的原理如图1所示。现有由0#、1#、2#三层介质构成的分层介质模型：0#与 2#介质层的特性阻抗均为z0，厚度都是正无穷；1#介质层厚度为D1，特性阻抗为z1，声速为c1。设0#介质层中有声源 A于无穷远处垂直向 1#介质层发射平面波sin(t)，sin到达 0#、1#介质层分界面时会产生反射波与透射波sT0(t)，而后sT0(t)在经过1#、2#介质层分界面的反射重新到达 0#、1#介质层分界面时会再次产生sR1(t)与sT1(t)，随后周而复始。此时1#介质层的反射波sR(t)的表达式为：

图1 离散脉冲法测量水声材料反射系数的原理示意图

在反射波的构成中，除去sR0(t)以外，所有的反射波分量都满足：

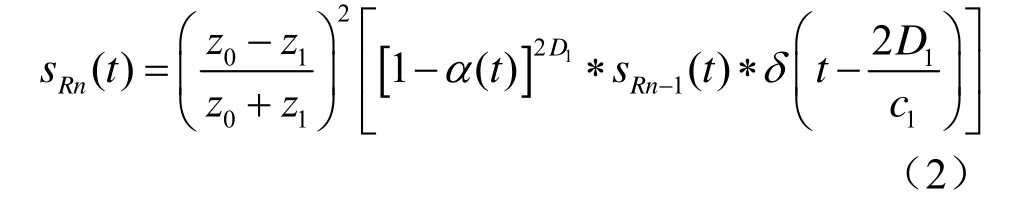
式中，“*”为卷积运算符，α(t)为1#介质吸声系数的时域表达式。对式（2）进行傅里叶变换后得到

式中，S(f)为s(t)的傅立叶变换，C(f)为SRn(f)与SRn-1(f)间的衰减函数：

将式（1）进行傅里叶变化，并将式（4）带入后得到

当反射信号时长趋近于正无穷时，SR(f)的表达式可以近似为

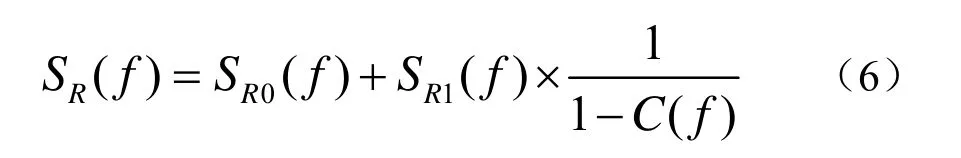
此时，1#介质层的反射系数R(f)可以表示为

式中，Sin(f)、SR0(f)和SR1(f)在Sin(t)有效时长小于2D1/c1时均可以在实验中测量得到，因此只要求出C(f)便可以得到1#介质层的反射系数。

根据分界面反射公式可以得到SR0(f)和SR1(f)之间的关系R01(f)：

代入式（4），可以得到R01(f)与C(f)间的关系：

式中

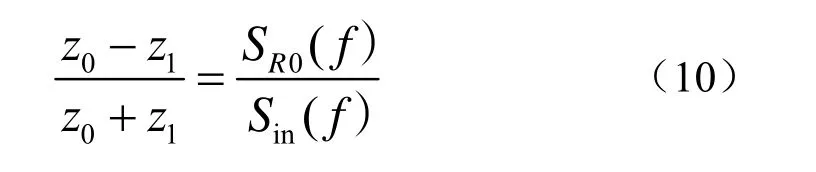
将式（10）代入式（9）中，得到C(f)的最终表达式：

由此，通过式（7）可以得到1#介质层的反射系数。

2 模拟计算

为了验证离散脉冲法测量材料反射系数理论的可行性，需要用传统材料反射系数计算公式（12）的结果[5]与离散脉冲法计算结果进行对比。

首先使用厚度为1 cm的有机玻璃板模型进行对比。公式中使用的有机玻璃的密度为 1.18×103kg/m3，声速为2700 m/s，对比结果如图2所示。

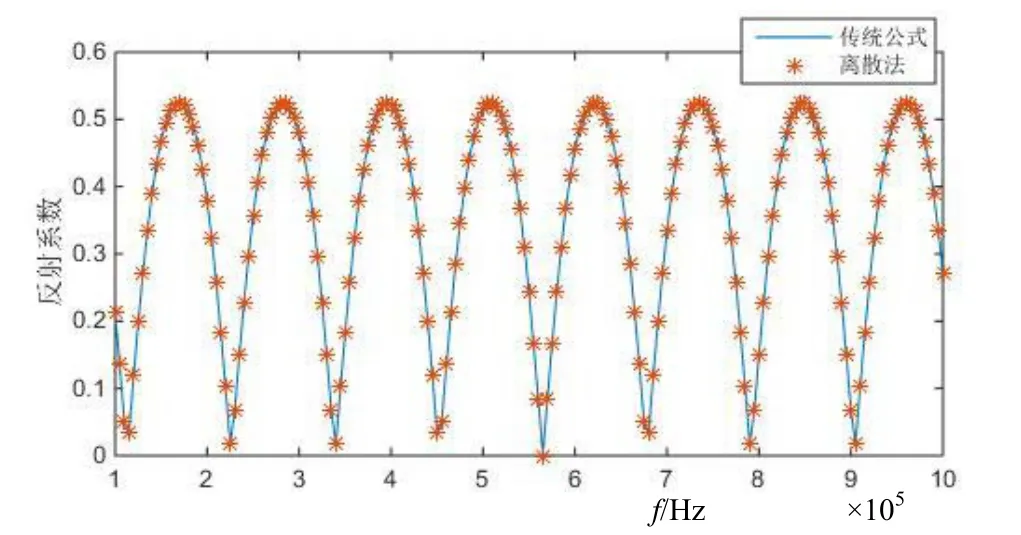
图2 有机玻璃板的反射系数计算结果对比图

而后使用厚度为1 cm的钢板模型进行对比。公式中使用的钢的密度为 7.8×103kg/m3，声速为6100 m/s，对比结果如图3所示。

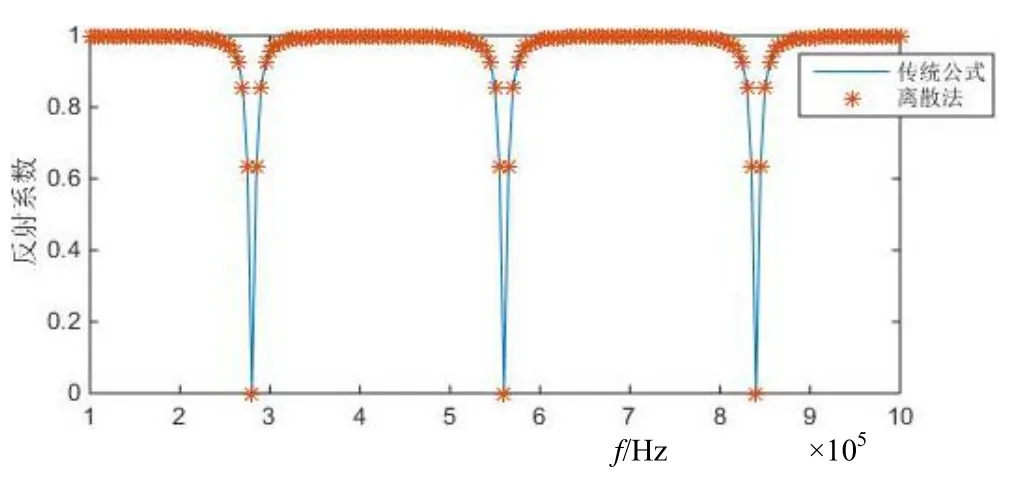
图3 钢板的反射系数计算结果对比图

通过两次模拟计算的结果可知，在被测材料的特性阻抗与水匹配失配情况下，都得到了一致的结果。由此可知，离散脉冲法测量水声材料反射系数在理论上是可行的。

3 实验验证

实验装置如图4所示。实验在尺寸为30 cm×30 cm×30 cm的有机玻璃水槽中进行。被测材料样品为1 cm厚、面积为20 cm×20 cm的有机玻璃板。水听器安装在被测材料几何中心轴上距离前表面 2 cm处；换能器最大有效尺寸为2 cm，谐振频率为1 MHz，远场距离为17 cm；换能器位于被测材料几何中心轴上距离前表面20 cm处，与水听器间距满足远场距离。实验时，先由信号源产生频率为 1 MHz的脉冲信号，脉宽为10-6s，经功率放大器放大后，传输至换能器；换能器受激励后发出声波，直达波及样品反射波由水听器接收；水听器与示波器连接，在示波器上观察水听器接收到的波形。

图4 离散脉冲法测量材料的反射系数实验装置

信号源输出的信号频率为1 MHz，周期数为1的正弦脉冲信号，但换能器的余振现象导致实际声信号的脉冲长度为 6个周期。根据式（8）可知，该方法仅需要测量直达波、前表面反射和后表面反射3个部分，截取后的信号如图5所示。而后在信号中分别截取这三种波作傅里叶变换得到Sin(f)、SR0(f)和SR1(f)，并代入式（8），求得在1 MHz频率下，厚度为1 cm的有机玻璃板的反射系数为0.28，与理论值0.270 7相差3.32%。实验结果符合文献[6]规定，由此可以证明离散脉冲法测量材料反射系数具有可靠性。

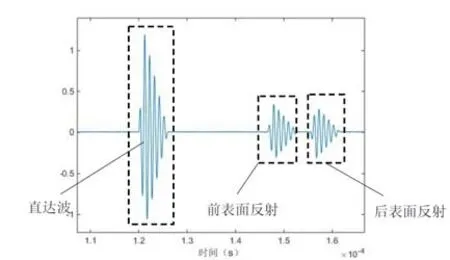
图5 离散脉冲法测量1 cm厚有机玻璃板反射系数的实验波形

有机玻璃吸声系数极小，可以忽略不计。因此C(f)的函数表达式中R01(f)可以简化为

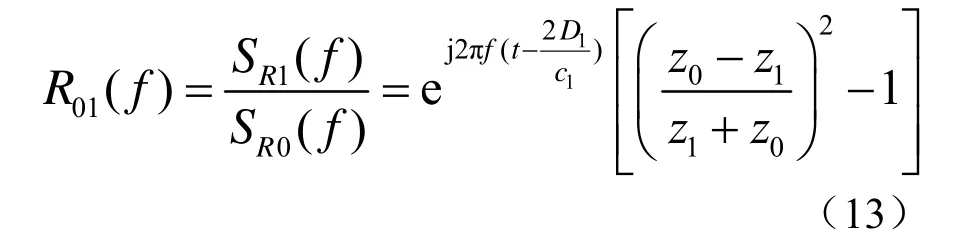
进而可以推导1 cm厚有机玻璃板在其他频率上的反射系数。经过计算1～50 kHz范围内，离散脉冲法推导的测量结果与式（12）计算的理论值对比如图6所示。可以看出推导值与理论值在反射系数随频率变化的趋势上基本相同，但在某些频率上与理论值相差较大。原因是材料的反射系数主要是通过直达波、前表面反射波和后表面反射波的幅值与相位信息推导出的，而1 MHz的相位信息对噪声的影响比较敏感，因此会造成较大的测量误差。另外，理论计算中有机玻璃的密度、声速与实际测量中使用材料的差别也会使结果产生差异。

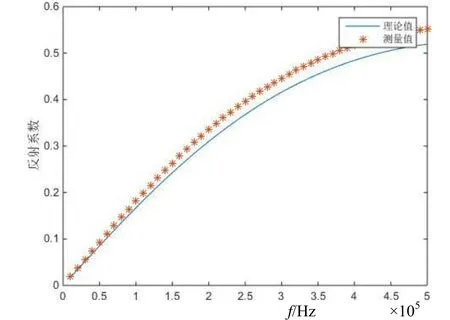
图6 离散脉冲法推导的测量结果与理论值对比

4 结论

通过仿真计算可知，离散脉冲法测量水声材料反射系数在阻抗匹配和失配情况下均具有可行性，实验验证了该方法在频率为1 MHz时，测量值与理论值间误差小于5%。根据实验数据推导1～50 kHz范围内被测材料的反射系数，推导值与理论值在反射系数随频率变化的趋势上基本相同，证明该方法测量水声样品的低频反射系数有效。材料的声速、吸声系数等性质均与声波的频率相关，会影响测量结果。文章中在试验部分仅使用了吸声性能差的有机玻璃验证离散法的可行性。为了进一步完善离散法，后续的工作可以研究在有限尺寸水槽中测量水声材料样品吸声系数和声速的方法，以拓展该方法的适用范围。