基于功率谱灵敏度的子结构损伤识别方法

方有亮， 李宗娆，张颖，娄佳琪

(河北大学 建筑工程学院，河北 保定 071002)

近年来，国内外学术界和工程界对于结构损伤识别的研究十分广泛和深入，并提出和发展了许多结构损伤识别方法.其中，功率谱密度是进行损伤识别与分析的有效用具.李曰兵等[1]采用废止铁路线钢桥为试件，利用正弦扫频波激振钢桥,分析其损伤前后加速度响应功率谱密度的变化来进行损伤识别. Gilbert-Rainer[2]针对相关信号段和相应谐波的整数周期计算每个信号分量的功率谱，提出了一种基于固有频率变化的梁式结构损伤检测及损伤位置和损伤程度评估的新方法.郑泽栋等[3]采用虚拟激励法计算功率谱密度对结构损伤参数的灵敏度，并结合有限元模型修正，对平面框架结构和剪力墙结构进行损伤识别.然而，在求功率谱灵敏度时，直接求取响应功率谱关于结构损伤参数的偏微分比较困难.

另外，大部分方法在对大型复杂结构的损伤诊断时需要较多自由度信息以及测点，因此实际工程中存在模态参数测量不完整的问题.为了提高计算效率，很多子结构识别方法应运而生.郑鸿飞[4]通过Guyan静力凝聚法对无砟轨道模型进行自由度缩减来降低结构自由度数目，并计算讨论了静力、动力学分析在无砟轨道分析中的适用性.侯吉林等[5]利用子结构响应的线性组合，采用子结构隔离法构造虚拟支撑，提出了一种改进的基于局部自由响应的子结构损伤识别方法.翁顺等[6]通过对子结构的模态解进行组集从而得到整体结构的模态解，从而应用于结构模型的修正与损伤识别.张青霞等[7]提出子结构的虚拟变形方法，利用子结构主要的虚拟变形来模拟损伤，在不重建结构有限元模型情况下，快速计算结构响应，提高了计算效率.

本文进行结构损伤识别时引入子结构的概念，采用Guyan缩聚法[8]先将整体结构划分为若干子结构，再组成凝聚后的整体刚度矩阵和质量矩阵，在此基础上进行结构的局部损伤识别；另外，在用功率谱灵敏度进行损伤识别的过程中，采用差分法进行灵敏度分析，解决了参数的偏微分较困难的问题；并采用多个频率下的功率谱来增加方程个数.通过以上方法，达到较少测点即可进行损伤识别的目的，提高了计算效率，并通过数值算例验证了方法的有效性.

1 差分法用于功率谱灵敏度分析

1.1 有限元方程与响应功率谱

多自由度结构受迫振动有限元方程为

(1)

其中，M为质量矩阵,C为阻尼矩阵,K为刚度矩阵.阻尼矩阵采用Raleigh阻尼模型

C=α1M+α2K.

(2)

结构在受地震随机激励、风谱激励等多点完全相干平稳激励的情形下，在频域范围内求解结构平稳随机响应的公式如下[9]：

S=H*SffHT,

(3)

其中，Sff为激励谱矩阵，H*、HT分别为频响函数矩阵的共轭和转置，S为待求的响应谱矩阵.

1.2 灵敏度矩阵的求取

基于灵敏度的结构损伤识别法，首先要得到结构模态参数或结构的动力响应对结构物理参数的灵敏度矩阵，再根据结构损伤前后的模态参数变化或动力响应的变化来求取结构物理参数的变化[10].

灵敏度在理论上是一个导数，如结构的响应功率谱(动力响应)对结构单元面积(结构参数)的灵敏度为∂S/∂A，对于自变量较少，矩阵维数较少的情况下，比较容易获得函数的导数；但是对于单元数量较多的复杂结构，直接采用导数方法求取灵敏度是比较困难的,有时甚至是不可微的[11].

设结构的单元损伤参数为A，假定结构有m个单元，n个自由度，假定第i个单元发生损伤，则取一个极小的损伤量ΔA，发生损伤后的单元参数矩阵为

A(I)=[A01…A0i+ΔA…A0m]T.

(4)

在损伤量为ΔA的情况下，功率谱变化矩阵

(5)

响应功率谱ΔS对损伤参数A的灵敏度矩阵如式(6)所示.

(6)

其中ω代表功率谱函数的频率，Sdij为损伤后的功率谱函数.上式为第i个单元损伤时的灵敏度矩阵，由于不能确定结构损伤的具体情况，即单元发生损伤的位置与数量，因此应当将功率谱矩阵中的所有元素分别对所有的单元损伤参数进行差分计算，为了使矩阵能够表达成一个方程组的形式，将n行n列的灵敏度矩阵写成一个n*n行一列的矩阵，即

(7)

(8)

(9)

1.3 超静定方程组的改进

在实际工程中，通过测量结构自由度功率谱响应来进行结构损伤检测时，通常是选择结构的部分测点测量，而不是将所有自由度一一测量，在这种情况下，式(9)所表示的超静定方程组的方程个数将会减少，当方程个数少于未知数时，将会难以求解或者误差很大.为了解决上述问题，本文采用功率谱的多个频点来增加方程的个数(但并不增加实验的次数)，可以通过测量几个自由度的响应，选取不同频率下的功率谱值，组成功率谱矩阵和功率谱变化矩阵，并求灵敏度矩阵,组成新的方程组，通过对其求解可得到损伤前后的结构损伤参数.

在本文的框架模型的数值模拟中，选取了4个自由度的响应，比如选择S11、S12、S13和S144个响应时，然后选择10个不同频率下的功率谱对损伤参数求取灵敏度矩阵，组成的方程组如式(10).

(10)

通过由式(3)计算的结构损伤前后响应功率谱，组成功率谱矩阵，并计算得到式(8)的灵敏度矩阵，代入并求解方程组(10)，即可将结构损伤参数识别出来.

1.4 损伤参数识别的迭代过程

当激励谱以及结构模型损伤前后测量的响应功率谱已知时，可以通过迭代的方法来识别结构损伤参数，用一条曲线来近似模拟迭代的过程(图1).

图1 功率谱函数迭代示意Fig.1 Iterative schematic diagram of power spectral function

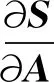
3)S(A3)与S2并不相等，重复以上步骤反复迭代直至得到A(i+1)和S2-S(A(i+1))，当S2-S(A(i+1))的值到达设定的允许值，即A无限接近结构实际损伤后的面积时，迭代结束.最后采用最小二乘法求解超静定方程组.

2 子结构的Guyan缩聚法

在实际的结构损伤识别问题中, 通过实验测量的振型通常是不完整的,当发生实测自由度数少于结构有限元模型自由度数的问题时,可以采用模型缩聚方法[12].

首先将整体结构划分为若干个子结构，对子结构进行模态特性分析，通过实施坐标凝聚，保留部分低阶模态，最后达到减少整体结构动力分析自由度的目的.

子结构的Guyan缩聚方法如下：

选择对接界面自由度为主坐标，用B表示；需要缩减的内部自由度为副坐标，用I表示,则子结构的运动方程为

(11)

忽略对接界面的惯性力，得到子结构的Guyan缩聚变换

(12)

其中，转换矩阵

(13)

缩聚后的子结构刚度矩阵和质量矩阵为

(14)

(15)

因此，子结构经Guyan缩聚后的运动方程为

(16)

在缩聚前结构的分析自由度为(nI+nB)，通过划分子结构并进行以上的缩聚，自由度缩减为nB，将缩聚后的子结构和未缩聚的子结构通过“对号入座”的方式组装，即可得到结构整体的动力学方程.

3 数值算例

3.1 整体结构的缩聚

图2为三层两跨的刚架，材料参数弹性模量E=2.06×1011Pa，密度ρ=7 800 kg/m3，截面长宽分别为0.031 m、0.008 m，每个单元长度均为0.28 m.该模型有15个单元，12个节点，36个自由度.

图2 整体结构Fig.2 monolithic construction

建模时，采用一致质量矩阵，比例阻尼系数α1、α2分别为0.000 5、0.000 1(对于数值模拟，阻尼比的取值对损伤识别结果影响较小), 用ANSYS(有限元建模软件)和MATLAB(有限元编程软件)对结构进行模态分析得到整体结构的前5阶频率.在划分子结构时，子结构划分不但要有利于各子结构的动态分析和整体的动力综合，更要尽量兼顾到实际结构加工装配过程中各部件的“天然”组合状态，如按实际结构的装配关系和几个形状的相对独立性划分；尽可能使各子结构的自由度数相近，避免刚度矩阵或质量矩阵的阶数相差悬殊；尽可能按同样的几何关系和边界条件划分，以减少各子结构特征值的计算次数等[13].因此将模型划分子结构如下图3、4所示.其中子结构1中节点5、6、7的自由度为界面自由度，节点2、3、4的自由度为内部自由度.

图3 子结构1Fig.3 Substructure 1

利用上文介绍的Guyan缩聚法将整体结构进行缩聚，将子结构1的内部自由度缩聚掉，经过缩减后的子结构1(只剩余界面自由度)凝聚到子结构2上，形成图5所示的结构.

图4 子结构2Fig.4 Substructure 2

图5 缩聚后的结构Fig.5 Polycondensed structure

采用MATLAB软件对缩聚后的模型进行求解运算，得到前5阶频率，并与缩聚前的整体结构的频率进行比较，结果见表1.

表1 前5阶频率比较

1)观察表1可知，ANSYS软件分析结果与MATLAB数值分析计算所得整体结构的前5阶固有频率基本一致.

2)对于Guyan缩聚法得到的结构，前3阶频率与原结构基本一致，由于被缩聚的内部自由度质量较大，随着频率升高，精度逐渐降低.

3.2 运用功率谱灵敏度分析法对缩聚结构的损伤识别

基于Guyan缩聚后的质量矩阵、刚度矩阵来求取结构的功率谱函数，进而采用差分法得到对损伤参数的灵敏度矩阵，并代入方程组(10)求解.假定子结构2各节点处作用一水平向左的平稳激励，采用功率谱曲线峰值点的左右两边等差取值选取频率.

3.2.1 单一损伤检测

采用减少单元面积的方法模拟损伤，首先进行单一损伤研究，假设缩聚结构的③号单元(即整体结构的⑮号单元)损伤29.43%，经过25次迭代，结果如图6所示.

图6表明能够成功检测出结构的单一局部损伤，其检测误差为0.008%，其他未损伤单元检测的最大误差为3.58%.

图6 单一损伤检测Fig.6 Identification of a single damage

3.2.2 多损伤检测

假设缩聚后模型的单元③、⑤、⑥(即整体结构的⑮、⑪、⑫号单元)分别损伤29.43%、22.40%、17.26%，经过35次迭代，损伤检测结果如图7所示.

图7 多损伤检测Fig.7 Identification of multiple damages

图7表明能够检测出结构多个位置的损伤，最大误差为1.04%，其他未发生损伤单元检测的最大误差为0.39%.

4 结论

本文提出利用差分法进行灵敏度分析，避免了偏微分计算，并采用选取功率谱函数和频率的方法达到了使用少量传感器测量响应功率谱，就能较准确检测出结构单一、多个位置局部损伤的目的.同时，通过子结构的Guyan缩聚大幅度缩减结构自由度，提高了计算效率.研究表明该方法具有良好的应用前景，但是,在实际的工程运用中，对噪声的影响以及系统进入非线性状态的损伤识别等问题有待深入研究.