基于非均等排序集抽样的Wilcoxon符号秩检验
2020-07-23董晓芳张良勇王志军
董晓芳,张良勇,王志军
(河北经贸大学 数学与统计学学院,河北 石家庄 050061)
排序集抽样(RSS)方法是澳大利亚农业学家Mclntyre[1]在估计农场牧草产量时提出的,已被广泛应用到临床医学、生态环境、可靠性工程、农林业等领域[2-5].排序集样本不仅包含了样本信息,还包含了次序信息,在实际中只要感兴趣的样本不易具体测量,但较容易直观排序时,RSS方法比简单随机抽样(SRS)方法更加有效.例如Risch等[2]论证了对配对亲属进行排序集抽样,遗传相关性实验效率能得到显著地提高.
RSS方法又被称为均等RSS,因为它包含各次序的信息相等.然而,随着RSS方法的深入研究,人们发现对于某些统计问题,并不是所有次序的信息都有用.非均等排序集抽样(RSSU)方法是Bhoj[6]在估计总体均值时提出的,并给出了基于RSSU的最小均方估计量.Gemayel等[7]考虑了RSSU下对称总体中位数的估计问题.Dong等[8]分析了RSSU下强度-动力可靠度的估计问题.张良勇等[9]研究了RSSU下总体中位数的符号检验.这些文献通过比较估计效率和检验功效,都证明了RSSU方法的抽样效率一致高于RSS方法.
RSSU方法的抽样过程为:第1步,从总体中随机抽取大小为m2的简单样本,分为m组,第i组单元数为mi=2i-1,i=1,2,…,m;第2步,利用直观感知信息对每组进行从小到大的排序,这些信息包括主观比较、专家观点等易于获得的信息,但不包括具体测量;第3步,从第i组抽取次序为i的样本单元,i=1,2,…,m.以上过程称为一次循环,为了扩大样本量,循环重复k次,这样就得到样本量为n=mk的RSSU样本X(i:2i-1)j,i=1,2,…,m;j=1,2,…,k,其中X(i:2i-1)j表示在第j次循环中从第i组中抽取次序为i的样本单元,最终只对这n个样本单元进行实际测量.RSSU样本的显著特点有:样本单元之间相互独立;对于给定的i,X(i:2i-1)1,X(i:2i-1)2,…,X(i:2i-1)k均与样本量为2i-1的简单随机样本中位数的分布相同.
为了提高未知总体对称点的检验功效,本文构建了RSSU下Wilcoxon符号秩检验统计量,分析其统计性质,计算Pitman效率,并比较检验功效.
1 基于RSSU的Wilcoxon符号秩检验统计量
设未知总体X的概率密度函数和分布函数分别为f(x-θ)和F(x-θ),函数f(t)连续且满足f(-t)=f(t).下面检验X的对称点θ是否等于θ0,即检验问题为
H0∶θ=θ0↔H1∶θ≠θ0,
(1)
其中H1∶θ<θ0和H1∶θ>θ0分别对应左单侧和右单侧检验.此检验问题称为对称点检验问题.
令X(i:2i-1)j,i=1,2,…,m;j=1,2,…,k为抽自X的RSSU样本.X(i:2i-1)j的概率密度函数和分布函数分别为
(2)
(3)
基于RSSU的Wilcoxon符号秩检验统计量定义为
其中I{·}为示性函数,R+(|X(i:2i-1)j-θ0|)称为X(i:2i-1)j-θ0的绝对秩,表示|X(i:2i-1)j-θ0|在|X(i:2i-1)j-θ0|,i=1,2,…,m;j=1,2,…,k从小到大排序中的秩.
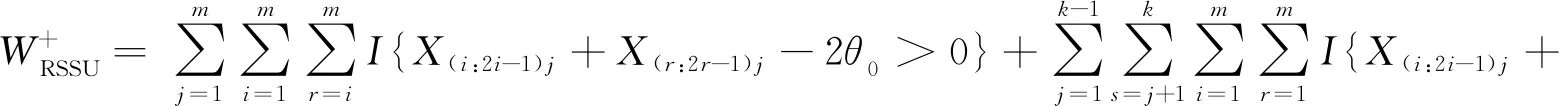
(4)
其中
2 新检验统计量的统计性质
首先分析关于X(i:2i-1)j的概率密度函数和分布函数的统计性质.
定理1若f(-t)=f(t),则
1)f(i:2i-1)(-t)=f(i:2i-1)(t),
2)F(i:2i-1)(-t)=1-F(i:2i-1)(t),
证明:1) 由已知可得f(-t)=f(t)和F(-t)=1-F(t).再由公式(2),得
2) 由结论1)可直接得证.
3) 由结论1)和2),得
定理得证.
证明:当H0成立时,根据公式(4)的第1个等式、F(t)的严格单调连续性和定理1,有
其中U(i:2i-1)j,i=1,2,…,m;j=1,2,…,k是抽自均匀分布(0,1)的RSSU样本.于是在H0下WRSSU的分布与总体分布无关.
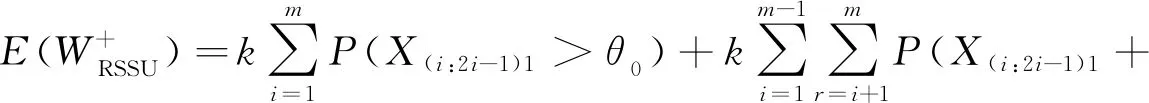
(5)
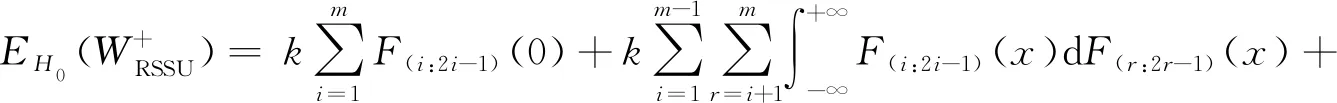
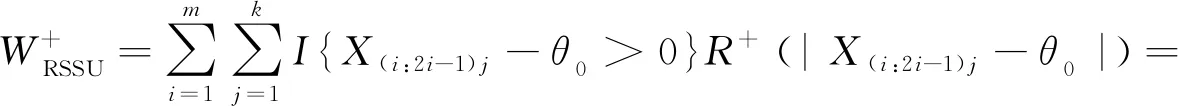
定理得证.
由公式(4),得
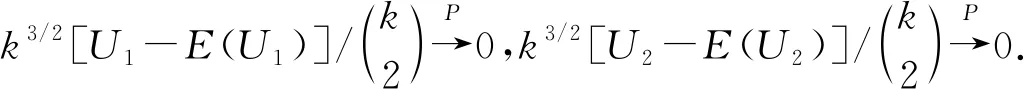
定理3当k→∞时,
其中
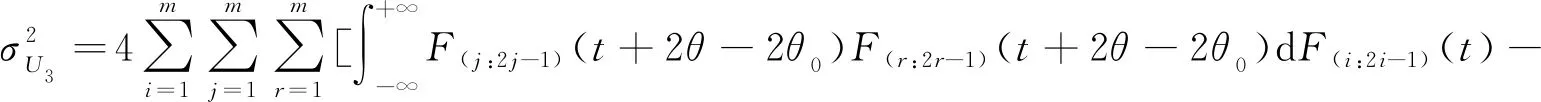
(6)
特别地,当H0成立时,
(7)
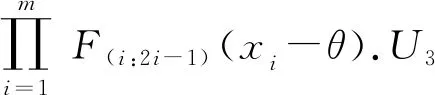
(8)
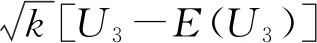
(9)
由公式(8)和定理1,得
E[hU3(X1,X2)hU3(X1,X3)]=
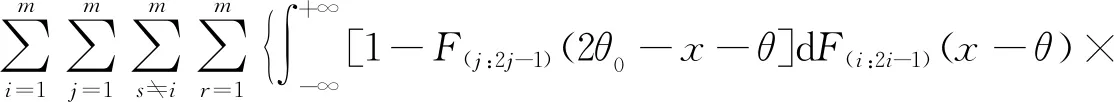
(10)
(11)
再将公式(10)和公式(11)代入公式(9),整理后即得公式(6).
当H0成立时,由公式(2)、(3)和(6),再根据定理1,得
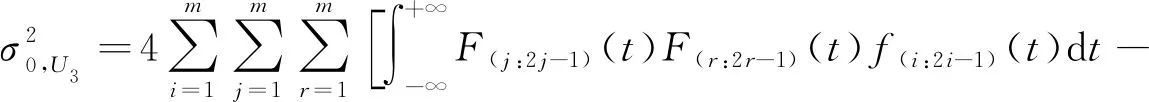
整理后即得公式(7),定理得证.
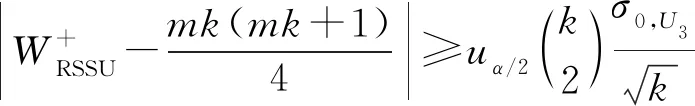
3 Pitman渐近相对效率
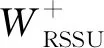
(12)
由公式(5),得
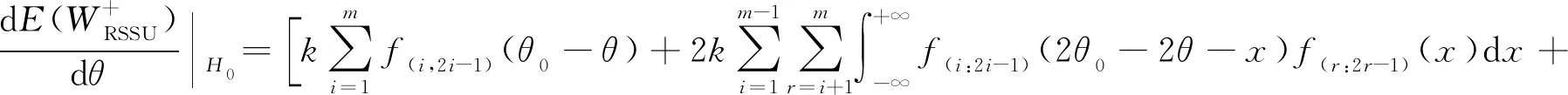
(13)
将公式(13)代入公式(12),再由公式(2)得,
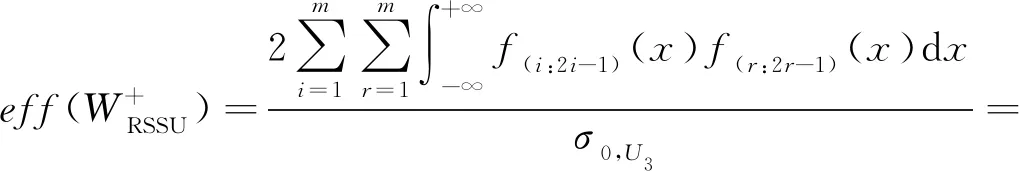
(14)
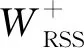
(15)
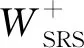
(16)
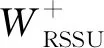
(17)
(18)
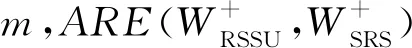
为了计算检验效率,总体分布F(x-θ)选取了4个峰度值由小到大的对称分布:正态分布N(θ,1)、Logistic分布L(θ,1)、Laplace分布LA(θ,1)、Cauchy分布C(θ,1).
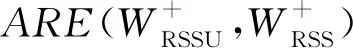
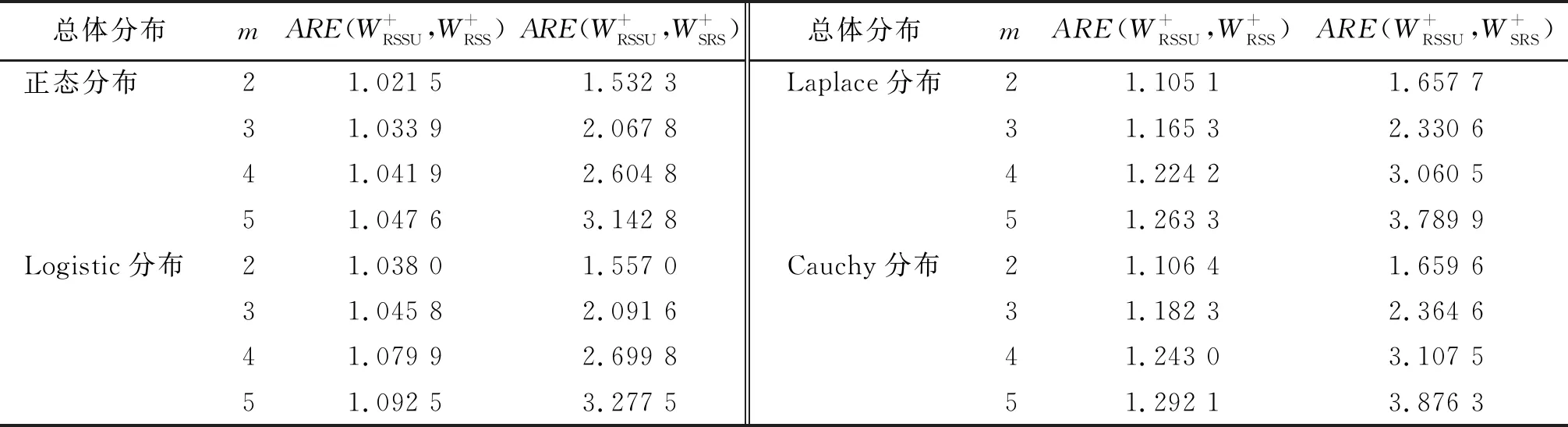
表1 Wilcoxon符号秩检验的Pitman渐近相对效率
4 结论