气动伺服系统的BELC 压力控制

宋玉宝，赵国新，刘昌龙，2，刘 昱

（1.北京石油化工学院机械工程学院，北京102617；2.北京化工大学信息科学与技术学院，北京100029）

1 引言

神经网络、滑模控制、鲁棒控制等智能控制算法被应用于气动伺服系统的压力控制。文献[2]将神经网络和辨识器结合应用于气动伺服系统，有效消除了气体的压缩性和摩擦力时变性带来的非线性影响。但该神经网络算法输入项过多，训练过程长，算法复杂度较高。文献[3]将混沌粒子群算法与滑模干扰观测器结合，提出一种改进的滑模控制器用于用于气动伺服系统，仿真表明，该改进控制策略对气动伺服系统的时滞和非线性表现出了较好的抑制能力，气动系统控制性能良好。文献[4]利用自适应学习和滑模控制设计了一种自适应鲁棒控制器，通过在线参数估计减小了模型参数的不确定性和参数估计误差。针对气动伺服系统非线性特点各智能控制算法进行算法融合与改进，虽然取得了一定的控制效果，但算法实现过程过于比较复杂，只针对其控制对象较为有效，而对其他对象适用性差，因此，针对气动伺服控制系统，寻找一种算法复杂度低，实现过程相对简单，而控制效果较好的控制算法是研究重点。

大脑情感学习模型（Brain Emotion Learning Controller，BELC）在20 世纪末被提出[5]，随后迅速发展并应用于控制工程，文献[6]将BELC 用于参数时变的步进电机运动控制，系统表现出较强的干扰抑制能力。文献[7]将BELC 应用于转台伺服系统，对非线性影响因素有较强的抵抗能力。这些研究应用表明BELC 在非线性系统控制中的优良性能和巨大潜能。基于以上研究现状，提出将BELC 用于气动伺服系统的压力控制，结合气动系统非线性和BELC 控制特性，对BELC 进行算法改进，采用模糊控制在线调整BELC 权值学习率。

2 气动伺服系统模型

2.1 气动伺服系统结构

气动伺服系统结构原理图，整个控制系统分为五部分，分别为气源、控制阀、传感器、执行元件以及控制器，如图1 所示。气源由气泵，储气罐，滤清器，减压阀组成，控制阀选用三位五通比例流量电磁阀，传感器为用于检测气缸内压力的气体压力传感器，执行元件为无摩擦气缸，控制器由数据采集板卡和工控机组成，数据采集板卡用于接收传感器的电信号并将工控机信号传送到比例阀，工控机则实现气动系统信号处理、气动系统控制算法编写等。

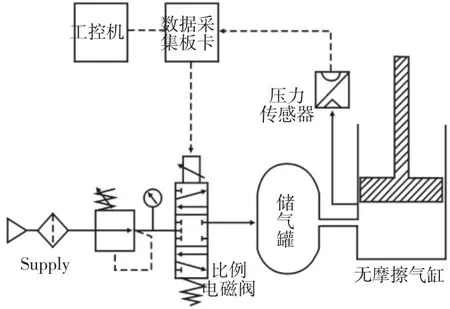
图1 气动伺服系统结构原理图Fig.1 Structure Principle of Pneumatic Servo System

2.2 气动伺服系统模型

气动伺服系统的本质是气体的压力控制。气缸压力为系统的控制目标，建立压力控制系统二阶模型：

式中：k1、k2、kL—待定系数；R—理想气体常数；k—气体比热比；

u—气体流动速度；V0、Ac—气缸的无效容积和有效截面积；

物流行业的发展在迈向未来的过程中必将逐渐走向智能化，特别是在仓储管理领域中表现的更为明显。劳动强度大、重复性较强、危险大的复杂劳动都可由智能机器人来出色完成。但是，我国对专门从事物流工作的智能机器人研究才刚刚起步。本文主要是对智能仓储机器人的运用现状进行调查，分析其对提升仓储物流效率有何作用，列出其优缺点并提出改善建议。

T—气体温度；Cf—流量系数；Pu、Pd—气流通道前后压力；

Av—阀口节流面积；Pc—气缸压力；φ（Pu，Pd）—流量函数。

定义状态变量X=［x1，x2］T=［pc，c］T，令y=Pc，作为系统输出变量，对输出压力进行微分得到系统的状态方程：

式中：Vc—气缸有效容积；m0—待定系数；d0—系统干扰和模型不确定系数；d—系统的总不确定量参数，yc及其一阶导数、二阶导数分别表示气缸活塞的运动位移、速度和加速度。

3 基于BELC 的压力控制

3.1 BELC 基本结构和工作原理

BELC 是一个有监督的网络算法。该控制器为无模型控制，且具有快速响应和干扰抑制的能力。它模仿大脑中负责情感处理部分的杏仁核、眶额皮质、丘脑和感官输入。从根本上讲，BELC是一种基于感官输入和情绪线索的行动生成机制。BELC 模型的基本结构，如图2 所示。

图2 BELC 模型基本结构Fig.2 Basic Structure of BELC Model

BELC 首先通过丘脑接收感官输入信号，经丘脑预处理后，将输入信号发送给杏仁体和感觉皮层。杏仁体和眶额皮质则处理从周围环境获得的信号，计算各自处理结果值。最后控制器输出由杏仁体和眶额皮质的处理结果值作差得到。

在模型中，对于每一个感官输入信号Si，杏仁体都有一个用向量表示的节点输出值Ai与之对应。其中，Ath表示杏仁体接收到的来自丘脑的最大刺激信号节点输出值。丘脑与杏仁体之间的这条路径称为丘脑连接。该刺激信号可以使杏仁体做出最快但不一定是最正确的响应。

每一个杏仁体的节点输出值Ai都等于预置可变连接权重Vi与相应输入信号Si的乘积。而在眶额皮质中也有与杏仁体节点输出值Ai类似的眶额皮质节点输出值Oi。其节点输出值等于其连接权重Wi与相应输入信号Si的乘积。综上，两者的节点输出值，如式4 所示。

杏仁体节点调节律，如式5 所示。奖励信号REW 和杏仁体节点差值决定了杏仁体连接权重Vi的更新，进而促使杏仁体学习过程的进行。学习速率是由常数α 决定。式中max 表示连接权重Vi不能减少，该定义表明：一旦杏仁体学习到特定赋值，就会保持下去。

眶额皮质节点调节律，如式8 所示。眶额皮质的自适应权重Wi与杏仁核的更新规则类似。只是眶额皮质的权重可以减小或增大，以调整杏仁体不合适的响应。参数β 为眶额皮质的学习速率常数。其中E*表示不含有丘脑连接信号的杏仁体输出与眶额皮质的差值。

最终的模型输出的结果值为杏仁体节点输出值和眶额皮质节点输出值的差值，如式8 所示。

由以上分析可知，BELC 通过丘脑连接产生最快的响应，在杏仁体中根据奖励信号进行学习预测，并保持学习结果。在眶额皮质中根据预测值和奖励信号的差值对控制器的输出进行抑制，最终使模型做出快速而准确的响应。

3.2 权值学习率的模糊控制

图3 不同学习率下的阶跃响应Fig.3 Step Response Under Different Learning Rates

BELC 的权值学习率包括杏仁体权值学习率α 和眶额皮质权值学习率β。前者决定了杏仁体权值学习过程的快慢，进而影响到系控制效果。而后者则直接影响眶额皮质权值学习过程的快慢，进而影响控制器输出的自身校正。取α 和β 不同数值进行0.1MPa 下的压力阶跃响应仿真实验，取值1：α=0.08，β=0.06；取值2：α=0.07，β=0.06；取值3：α=0.06，β=0.05；取值4：α=0.06，β=0.04；取值5：α=0.05，β=0.03；取值6：α=0.04，β=0.02；实验响应结果，如图3 所示。

不同权值学习率对应不同的阶跃响应结果。为提高系统控制性能，采用模糊控制对权值学习率进行在线调整。针对不同权值学习率下的系统响应结果进行分析，制定权值学习率和系统压力误差e及压力误差变化率ec之间的模糊控制关系，将权值学习率和系统压力误差e及压力误差变化率ec之间的关系转化为用自然语言表述的控制策略，再依照该控制策略进行权值学习率的调节，实现权值学习率的模糊控制。

结合模糊控制的输出变量Δα 和Δβ，则权值学习率的在线调整公式为：

式中：α0、β0—设定的初始权值学习率，起始时令α0=0.06，β0=0.04，通过模糊控制获得在线调整的α 和β 的数值用于BELC 的实际压力控制。

3.3 BELC 的压力控制

将BELC 用于气动伺服系统的压力控制，针对气动伺服系统特点，选取基于误差形式的感官输入信号（SI）函数和奖励信号（REW）函数，对两者设定如下：

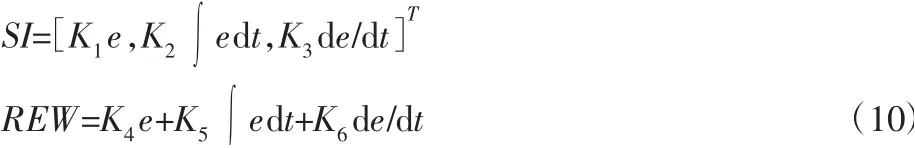
式中：e—压力误差；

K1～K5—调节系数。

基于BELC 的气动伺服控制系统图，如图4 所示。根据给定压力值和实际压力反馈值获得压力误差，压力误差进而传递到选取的感官输入信号函数和奖励信号函数中，同时，压力误差及其变化率经模糊控制后，获得BELC 相应的权值学习率，用于BELC的学习过程。经BELC 模型处理后得到的比例阀的控制电压用于气动伺服系统的控制。

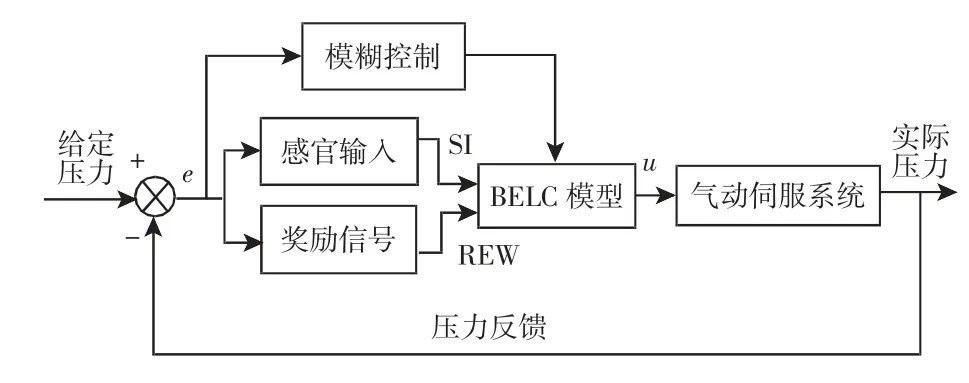
图4 基于BELC 的气动伺服控制系统图Fig.4 Pneumatic Servo Control System Based on BELC

4 实验及结果分析

搭建气动伺服系统实验平台，分别采用PID，BELC 以及BELC改进算法进行压力控制实验。

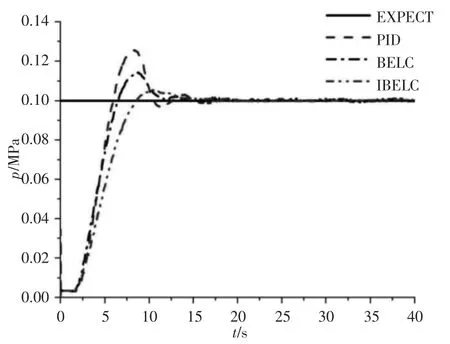
图5 0.1MPa 下的阶跃响应Fig.5 Step Response Under 0.1MPa

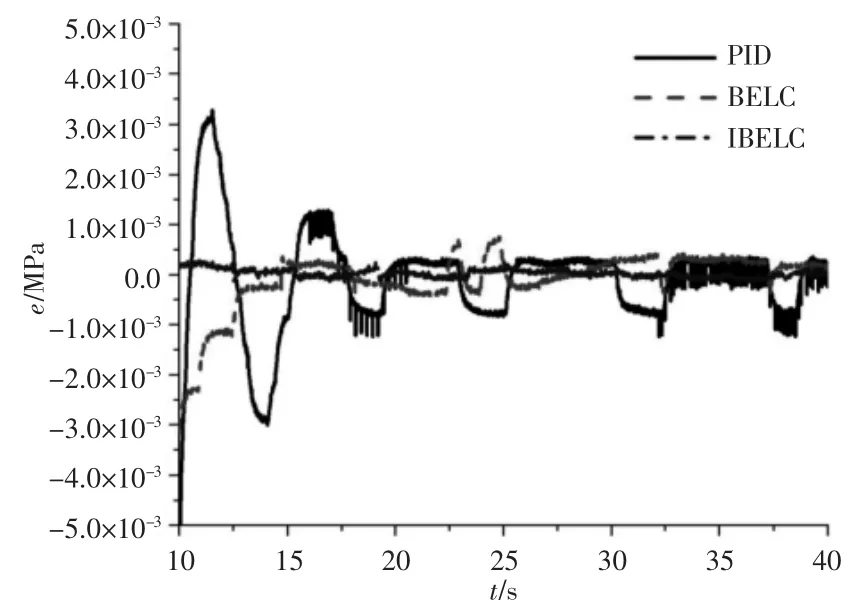
图6 0.1MPa 下的阶跃响应误差Fig.6 Step Response Error Under 0.1MPa

PID 的稳态时间约为19.8s，稳态误差约为1750Pa；BELC 的稳态时间约为16.2s，稳态误差约为937Pa；IBELC 的达稳态时间约为15.3s，稳态误差约为411Pa，如图5、图6 所示。BELC 较PID 的稳态时间缩短了18.2%；稳态误差降低了46.5%；IBELC 较PID 的稳态时间缩短了22.7%，稳态误差降低了76.5%；IBELC 较BELC 到达稳态时间减少了5.6%，稳态误差降低了56.1%。在42s 时给予一瞬态突变扰动，PID 产生最大超调为116.32KPa，再次到达稳态的时间为10.1s；BELC 产生最大超调为106.76KPa，再次到达稳态的时间为8.6s，IBELC 产生最大超调为102.15KPa，再次到达稳态时间使用了6.3s，如图7 所示。BELC较PID 超调量降低了8.21%，再次达到稳态的时间减少了14.85%，IBELC 较PID 超调量降低了12.18%，再次达到稳态的时间减少了37.62%。在跟踪幅值为0.1MPa，频率0.04Hz 的正弦跟踪响应中，PID在（35～60）s 的周期内幅值衰减了11.81%，相位滞后了1.24s，如图8 所示。BELC 在（35～60）s 的周期内幅值超调了8.73%，相位滞后了0.83s。IBELC 在（35～60）s 的周期内幅值超调了3.57%，相位滞后了0.52s。

图7 0.1MPa 下的42s 处阶跃扰动Fig.7 Step Disturbance at 42s Under 0.1MPa

图8 幅值0.1MPa，频率0.04Hz 的正弦响应Fig.8 Sinusoidal Response of Amplitude 0.1MPa and Frequency 0.04Hz

5 总结

将BELC 用于气动伺服系统的非线性压力控制，采用模糊控制对BELC 权值学习率进行在线调整。实验结果表明：BELC 改进算法较PID 在响应速度和稳态精度上有明显提高。稳态误差稳定在（400～500）Pa 之间，存在扰动时，稳态时间降低了30%以上，BELC 改进算法具有更强的鲁棒性。在动态跟踪中，幅值变化和相位滞后小，跟踪效果更好。综上研究表明BELC 改进算法的可行性和在气动控制方面的良好适应能力。