基于遗传算法的车辆跟驰行驶模糊控制研究

孙永厚，王 萌，刘夫云，尹 帅

（1.桂林电子科技大学机电工程学院，广西 桂林 541004；2.广西制造系统与先进制造技术重点实验室，广西 桂林 541004）

1 引言

车辆跟驰行驶是汽车驾驶过程中最基础的驾驶行为之一。跟驰理论是运用动力学的方法来研究前导车运动状态变化所引起跟随车辆的相应变化，通过分析两车之间的距离和相对速度，在保证安全性和舒适性的前提下，得到后车的应采取的操作措施，控制后车安全行驶。车辆在跟驰行驶过程中，驾驶员针对两车之间的距离和相对速度信息调整自车速度进行安全跟驰，由于距离和速度信息的不确定性，将模糊理论应用到车辆跟驰行驶研究中，通过模糊控制器建立跟驰行驶系统。然而对于模糊控制中隶属函数的确定，通常是根据专家经验，存在很大的主观性和随意性，利用遗传算法对隶属函数进行优化，得到的结果与车辆跟驰模糊控制进行对比，验证可知优化后的模糊控制能够保证车辆行驶安全，提高车辆跟驰行驶的平稳性，为车辆跟驰行驶模糊控制的研究提供了一次有益的尝试。

2 安全距离的确定

在同车道车辆跟驰行驶过程中，后车与前车需要保持一个合理的行车间距，这个距离既不会发生碰撞事故又能保持较好道路通行能力，就是行车安全距离。国内外学者对于行车安全距离进行了很多的研究，所依据的三种常用安全距离公式如下：

基于制动过程的理论安全距离公式[1]：

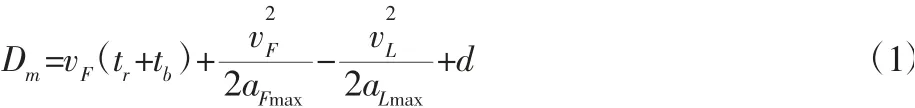
式中：vL、vF—前、后车的初始速度；tr、tb—驾驶人和车辆制动系统的反应时间；d—静止时两车之间的缓冲余量；aLmax、aFmax—前导车和跟随车的最大制动加速度。

国外研究人员对安全距离的确定进行了相关实验，在路况良好路面条件下，对48 辆装有真空助力制动装置的车辆进行了制动实验[1]，通过最小二乘法对实验数据进行拟合，得出了以下公式：

国内也进行了相关实验，根据文献[2]，得到驾驶员在稳速跟车状态下与前车期望保持的距离公式：

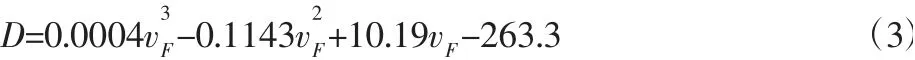
综合考虑三种常用的安全距离，通过最小二乘法拟合的方法，利用Matlab 软件中的ployfit（x，y，n）函数进行拟合，得到车辆跟驰行驶安全距离公式如下：

3 基于遗传算法的模糊控制器

模糊控制适用于多输入、具有不确定因素的非线性控制系统，其优点在于具有较高的稳定性和适应能力，广泛应用于智能控制、运动控制等方面。模糊控制规则和模糊变量的隶属度函数的选取是模糊控制器设计的关键，考虑到其本质是参数寻优的问题，将遗传算法引入到模糊控制中，遗传算法是一种全局搜索算法，非常适合用于模糊控制器的优化设计。

3.1 模糊控制器的建立

3.2 模糊控制器的优化

通常在模糊控制器的设计中，隶属函数主要靠专家的经验或反复试验的方法来调整和确定，从本质上来说，就是寻求最优化控制的过程。遗传算法[4]是一种模拟自然进化过程的自学习优化算法，借鉴自然界的优胜劣汰法则，对复杂问题的优化比一般的优化算法有其独特优点，适用于模糊控制器的优化。遗传算法的基本过程包括初始化种群、适应性评价、选择、交叉、变异等部分。操作步骤，如图1 所示。

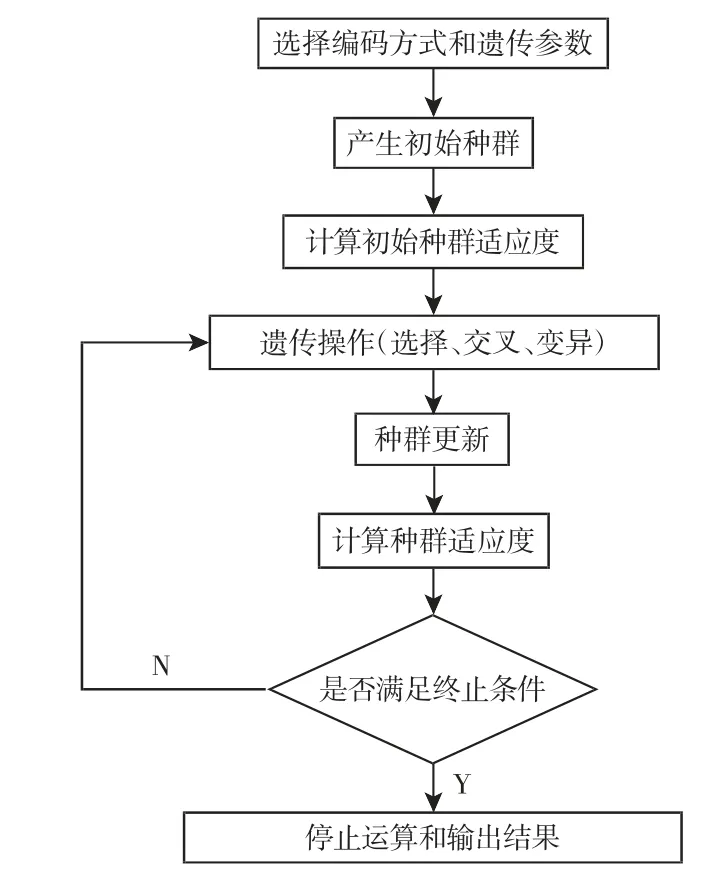
图1 遗传算法流程图Fig.1 Genetic Algorithm Flow Chart

模糊控制器是模糊控制系统的核心部分，是建立完备控制系统的基础。模糊控制器是将专家经验或工程知识通过语言变量的方式描述其控制规则，利用这些规则去控制系统。

3.1.1 确定输入、输出量隶属函数

基于刺激—反应关系原理建立跟驰模型，以两车之间的实际距离与安全距离的差值（偏差值）ΔS和速度差Δv作为刺激[3]，确定为模糊控制器的输入量；以后车的加速度a作为反应，确定为模糊控制器的输出量。确立跟驰系统为一个双输入单输出的模糊控制结构。首先对输入输出变量进行模糊化处理，模糊集合均取7 个，分别用NB、NM、NS、ZE、PS、PM、PB来表示，代表的含义分别为负大、负中、负小、零、正小、正中和正大，模糊变量隶属函数的形状选择基础的三角形函数分布。

3.1.2 模糊推理规则

模糊推理的结论主要取决于输入量和输出量之间蕴含的关系以及模糊集合之间的合成运算法则。车辆跟驰系统采用双输入单输出的模糊控制器结构，系统的2 个输入量均有7 个模糊子集，故可构成49 条模糊规则，建立推理规则可表示为：

如果＜ΔS=E1＞且＜Δv=EC2＞，则＜a=K＞

模糊逻辑推理采用Mamdani 模糊推理法，利用重心法去模糊化。

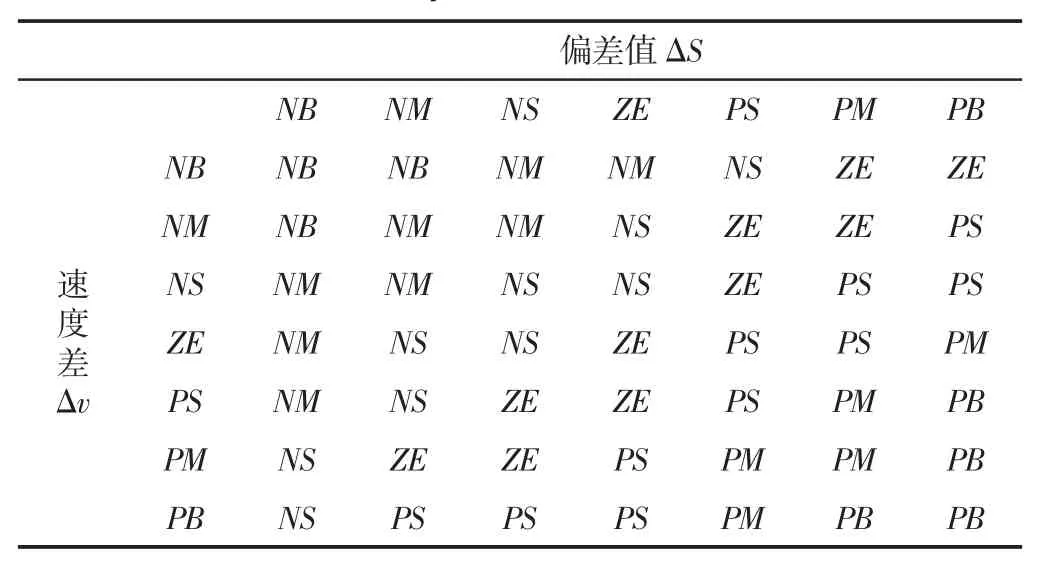
表1 模糊控制规则表Tab.1 Fuzzy Control Rules Table

3.2.1 编码

编码[10]就是将待优化问题的参数按照一定的规律编写成一系列的代码的过程。编码的方法有很多，二进制编码是相对简单的一种编码方式，但是如果待优化参数较多会造成编码串过长，会影响算法的收敛速度，且在运算时需不断地编码和解码，既使计算量增加，又使精度有所降低。相比二进制编码，十进制编码长度短，稳定性强，精度便于控制，运算效率高，因此采用十进制编码。

由模糊控制器的设计可知隶属度函数的的分布形式采用三角形函数分布。三角函数的模糊论域划分，每个模糊集合的范围是由顶点的横坐标wi、以及左右两端点到基点的距离ui、vi（i表示7 模糊语言变量）三个参数确定的，如图2 所示。如图3 所示，选取这三个参数作为优化参数，即可对隶属函数进行编码，隶属度函数的编码长度为63。

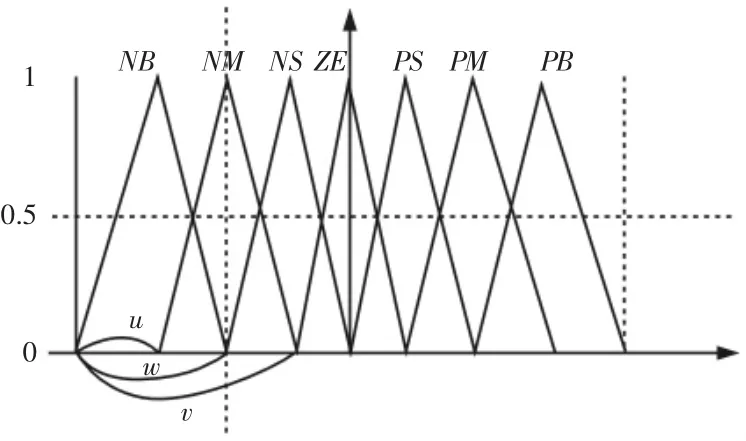
图2 模糊论域划分Fig.2 Fuzzy Domain Division

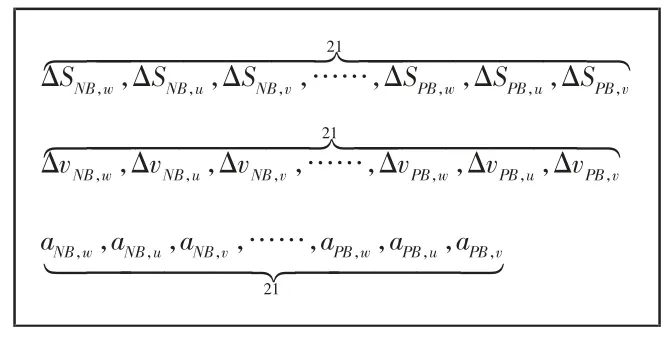
图3 隶属函数编码Fig.3 Membership Function Coding

3.2.2 适应函数

遗传算法在寻优过程中通过适应度的大小来评价个体的优劣，如果个体的适应度高，那么其被选择的概率就越大。而确定适应度值的函数便是适应函数。在处理实际问题时，适应度函数与优化问题的目标函数的关系是多样的，要求优化问题的最大值或者是最小值。

适应度函数的选取直接制约遗传算法的运算过程，影响优化结果。

采用如下形式的目标函数来评价控制器的性能：

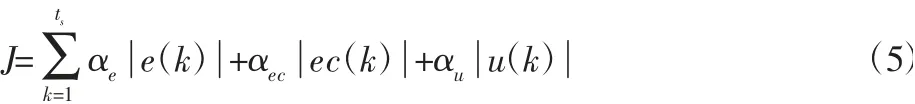
式中：ts—处理问题持续时间；αe、αec、αu—常数，分别为e（k）、ec（k）、u（k）的加权系数，决定了他们在目标函数中的比重，数值大小表明重视程度的高低。

遗传算法需要计算个体的适应度值，因此需要将目标函数转换成最值问题，确定转换函数为：

3.2.3 优化后的隶属度函数

利用MATLAB 软件进行优化计算，遗传算法的初始种群确定为50，目标函数中加权系数αe、αu分别取0.5、0.4、0.1，交叉率和变异率分别取1/50 和0.75，经过81 代得到最优解。

通过遗传算法优化后的模糊隶属函数，如图4～图6 所示。

图4 偏差值隶属函数Fig.4 Deviation Value Membership Function

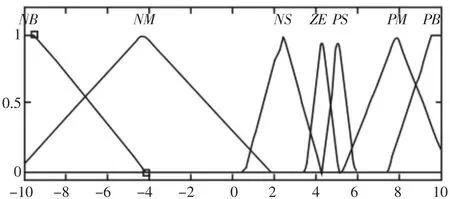
图5 速度差隶属函数Fig.5 Speed Difference Membership Function

图6 加速度隶属函数Fig.6 Acceleration Membership Function

4 车辆跟驰过程的仿真分析

在Matlab/Simulink 环境中，建立基于遗传算法的车辆跟驰行驶模糊控制仿真模型和车辆跟驰行驶模糊控制仿真模型。分别讨论当前导车匀速行驶、匀减速行驶两种工况下跟随车的反应，并且对两种跟驰模型的加速度和相对距离变化进行对比说明。建立两车跟驰行驶仿真模型，根据目标车辆、被控车辆行驶状态采取合理控制措施。被控车辆作出的决策被传送到执行机构从而控制车辆安全跟随前导车行驶。在Simulink 中搭建的仿真模型，如图9 所示。对于前导车不同的运动状态，要在模型中相应部分稍作改动，并设置对应参数，即可进行不同工况下的仿真模拟。分别通过对前导车匀速、匀减速两种典型的行驶工况，优化前与优化后的仿真结果进行仿真验证分析：

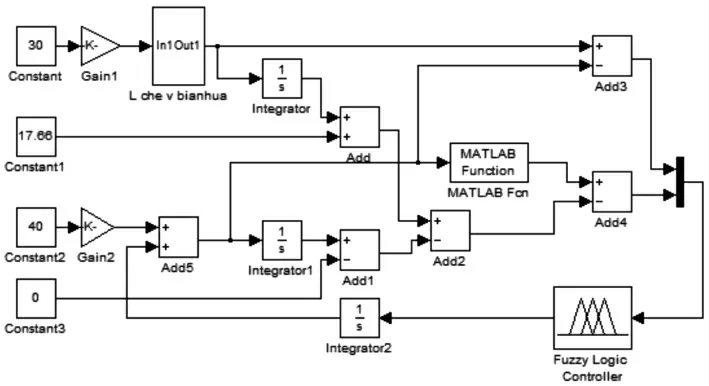
图7 Simulink 仿真图Fig.7 Simulink Simulation Diagram

工况1：

前导车匀速行驶。参数设置：跟随车速度分别为40km/h、100 km/h，前导车为30 km/h、80 km/h 且保持匀速行驶。

工况2：

前导车匀减速行驶。参数设置：跟随车和前导车的车速相等，分别为50km/h、120km/h，前导车且以-5m/s2的加速度制动行驶。

图8 工况1.a 仿真结果Fig.8 Case 1.a Simulation Results

图9 工况1.b 仿真结果Fig.9 Case 1.b Simulation Results

图10 工况2.a 仿真结果Fig.10 Case 2.a Simulation Results

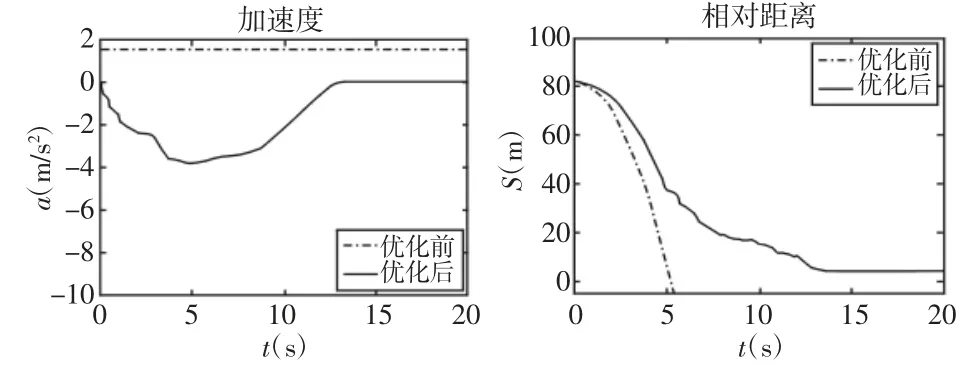
图11 工况2.b 仿真结果Fig.11 Case 2.b Simulation Results

通过图示仿真结果可知：当前导车匀速行驶时，车辆跟驰行驶模糊控制系统可以满足车辆在不同速度下的安全跟驰行驶，初始阶段加速度存在波动现象；基于遗传算法的模糊控制系统消除了波动现象，提高了驾驶员乘坐舒适性。当前导车匀速减行驶时，车辆跟驰行驶模糊控制系统在高速时不能满足车辆安全行驶，如图所示会在5s 时发生碰撞，且在低速跟驰行驶时，加速度存在剧烈波动现象；基于遗传算法的模糊控制系统解决了车辆高速行驶时安全跟驰行驶的稳定性，控制跟随车安全跟驰行驶，并且消除加速度波动，提高了驾驶员乘坐舒适性。通过两种不同工况分析，基于遗传算法的模糊控制输出加速度曲线平缓且加速度值较小，明显提高了车辆跟驰行驶平稳性；消除了车辆跟驰模糊控制在高速状态下的不稳定现象，跟驰车辆可以采取准确稳定的制动措施，保证两车行驶安全。

5 结论

首先根据车辆跟驰行驶的三种常用安全距离，通过最小二乘法拟合得到改进的安全距离；然后以改进安全距离为基础，通过模糊控制理论建立模糊控制系统；最后利用遗传算法对模糊控制的隶属度函数进行优化。利用Matlab/Simulink 软件，建立车辆跟驰行驶的仿真模型，对优化前后的车辆跟驰行驶模糊控制进行仿真对比验证。通过仿真结果可知，基于遗传算法的车辆跟驰行驶模糊控制使跟随车加速度更加平稳，既保证了车辆行驶的安全性，又兼顾行车舒适性。