海陆地震动的时频域工程特性对比

张 琪, 郑向远, 李 炜

(1.清华大学 土木工程系, 北京 100084;2.清华大学 深圳国际研究生院海洋科学与技术学部, 广东 深圳 518055;3.中国电建华东勘测设计研究院有限公司, 杭州 311122)

海洋资源的开发以及区域海上交通的建设离不开海洋工程的兴建，如海洋平台、海上风机、水下油气生产系统、海底隧道和跨海大桥等，保证海洋结构使用的安全性和可靠性尤为重要.坐底式海洋结构若建在地震活跃海域，其服役期内除了经受风、浪、流等环境荷载外，还会受到海底地震动的影响.然而，由于海底强震观测台网布设的欠缺以及海底场地条件复杂性等影响，针对海底地震动工程特性的研究相对较少，在中国尤其如此.

在早先的国外研究中，Boore等[1]选取了从美国SEMS(seafloor earthquake measurement system)系统中记录的9条海底地震动数据进行相关研究.由于数据量太少，缺乏统计意义，他们只对竖向(V)和水平向(H)地震动的傅里叶谱和反应谱(5%阻尼比)的谱比(V/H)进行了对比分析，结果发现由于海水层对P波高频能量的削弱作用，海底地震动的竖向成分比陆地竖向地震动的能量小，尤其是在短周期部分.刁红旗等[2]首先从地震学角度研究了海水对海底地震动竖向成分的影响，并在Boore等[1]的基础上分析了海底地震动的工程特性.研究表明海底竖向地震动受到海水的影响，高频能量被削弱，而在海底软土层影响下加速度反应谱的长周期成分会被放大.Dhakal等[3]搜集了日本K-NET(Kyoshin network)强震观测网中海底台站记录的海底地震动，研究了非线性场地条件对地震动的影响.他们将地震动根据峰值加速度PGA(peak ground acceleration)的大小分为强地震动和弱地震动，分析发现土层的非线性响应会造成地震动卓越频率成分向低频移动.陈宝魁等[4]对比分析了从SEMS和K-NET中获取的若干海陆地震动的PGA和反应谱.结果表明近海竖向PGA比陆地PGA低，而且在短周期部分海底反应谱比(V/H)低于陆地地震动.由于实测海底地震动数据有限，无法像研究陆地地震动特性一样充分考虑各种因素的影响，因此针对海底地震动特性的研究还不是十分成熟，尤其是海底地震动的时频域特性.另一些学者通过建立数值模型的方法研究影响海底地震动的因素.Nakamura等[5]使用有限差分法模拟了海底走滑震源的地震波场，研究结果强调了在进行地震动模拟中综合考虑海水和海底地形对地震动的影响很重要.Todoriki等[6]建立一维土层结构模型，利用有限差分法计算分析海水层对海底地震动的影响.发现海水层类似于低通滤波器，高频能量被削弱，所以在海底地震的模拟中考虑海水层的影响非常必要.然而数值模拟的方法始终是一种理论化方法，无法完全符合真实的震源特性或场地条件等，所得到的地震动特性与实际数据还有差距.

已有的研究表明海底地震动和陆地地震动具有不同的动力特性，然而目前针对海洋结构物的抗震设计和安全评估仍然是参考陆地地震动的有关性质和规范开展的，比如美国著名的API规范[7].由于海陆不同土层结构以及海底上覆水层等的影响，造成海陆地震动工程特性的不同，利用陆地地震动记录指导海洋结构物抗震设计是不尽合理的.Smith[8]指出由于海底土层和地质条件、海水层的影响，海底地震动的特性与陆地地震动有区别.另外，因为海洋结构构造的特殊性(如深桩基、质量集中在结构顶端等)，会使得海洋结构物的地震响应呈现出与陆地结构不同的特征.吕悦军等[9]通过获取渤海PL19-3油田的工程场地土层结构，分析了海底土层的动力特征，结果表明海底表层软弱土对地震动反应谱有显著影响，而现行规范中针对陆地场地土类型划分标准不能反映海底淤泥层的特征.因此，海洋结构抗震设计以及动力响应分析需要使用海底地震动作为荷载输入才能获得准确的结果，从而合理地进行结构设计以及安全性校核.

将海底地震动与陆地地震动加以区分，并将海底地震作为独立课题进行研究，揭示海底地震动独特的时频域工程特性，并且利用真实的海底地震记录作为地震荷载输入，进行结构的动力响应时程分析，这对于海洋结构物的抗震设计和安全评估具有重要意义.基于此目的，本文收集了K-NET地震观测系统中6个海底观测台站记录的23场地震的海底地震动，以及相应的陆地地震动，形成了一个含有一千多条地震动的数据库，并从中选出69对海陆地震动数据.每一对海陆地震动记录来源于同一场地震，且它们的震中距基本相同，由此分析了它们地震动三要素[10](PGA、持时和反应谱)的差异，以及能量在时间-频率分布上的特性.

1 数据选取

日本K-NET系统[11-12]基本遍布日本陆地，其中也包含了位于相模湾海域的6个海底观测台站，SR1- SR6，见表1.这6个台站间距不超过20 km，且近似直线分布[13]，它们的平均海拔为-1 500 m左右.本文从中选取了K-NET系统中23场地震的海底地震动，以及相应的10个附近陆地台站(LR1- LR10)记录到的陆地地震动，并对原始数据进行了基线校正和滤波处理[14]，共组成了1 086条地震动数据库.这23个地震活动中包括18个震源在海底的海底地震(SE)以及5个震源在陆地的陆发地震(LE)，大部分地震的震源深度不超过70 km，其中包括了2011年3.11“东日本大地震”，震级为Mw9.0[15].

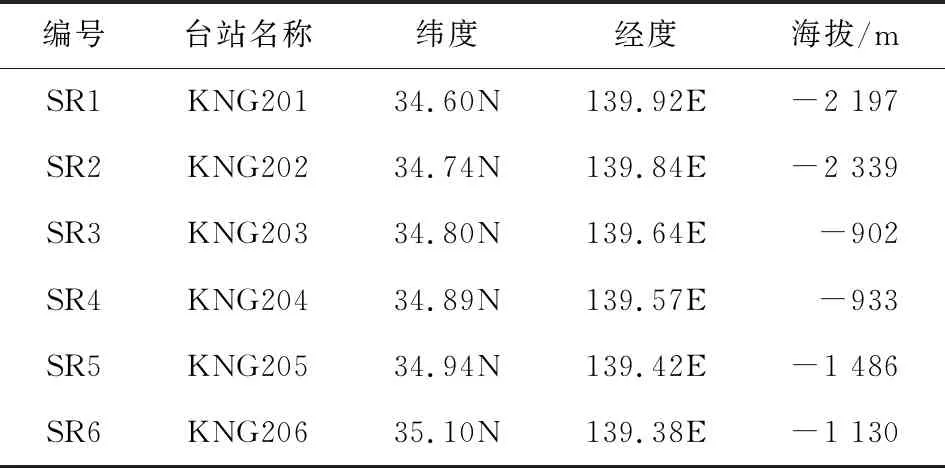
表1 日本K-NET系统中6个海底台站

由于地震动特性受震级和震中距影响很大，为了研究场地条件对海底地震动动力特性的影响，本文从数据库中选取了69对数据进行对比分析.其中每一对包含了同一场地震中分别从一个海底台站和一个陆地台站记录到的三方向地震动，即两条水平向(EW和NS)以及一条竖向记录，且这两个台站所对应的震中距基本相同.

表2给出了23场地震的相关信息以及从每一场地震中选出来的数据对的数量.

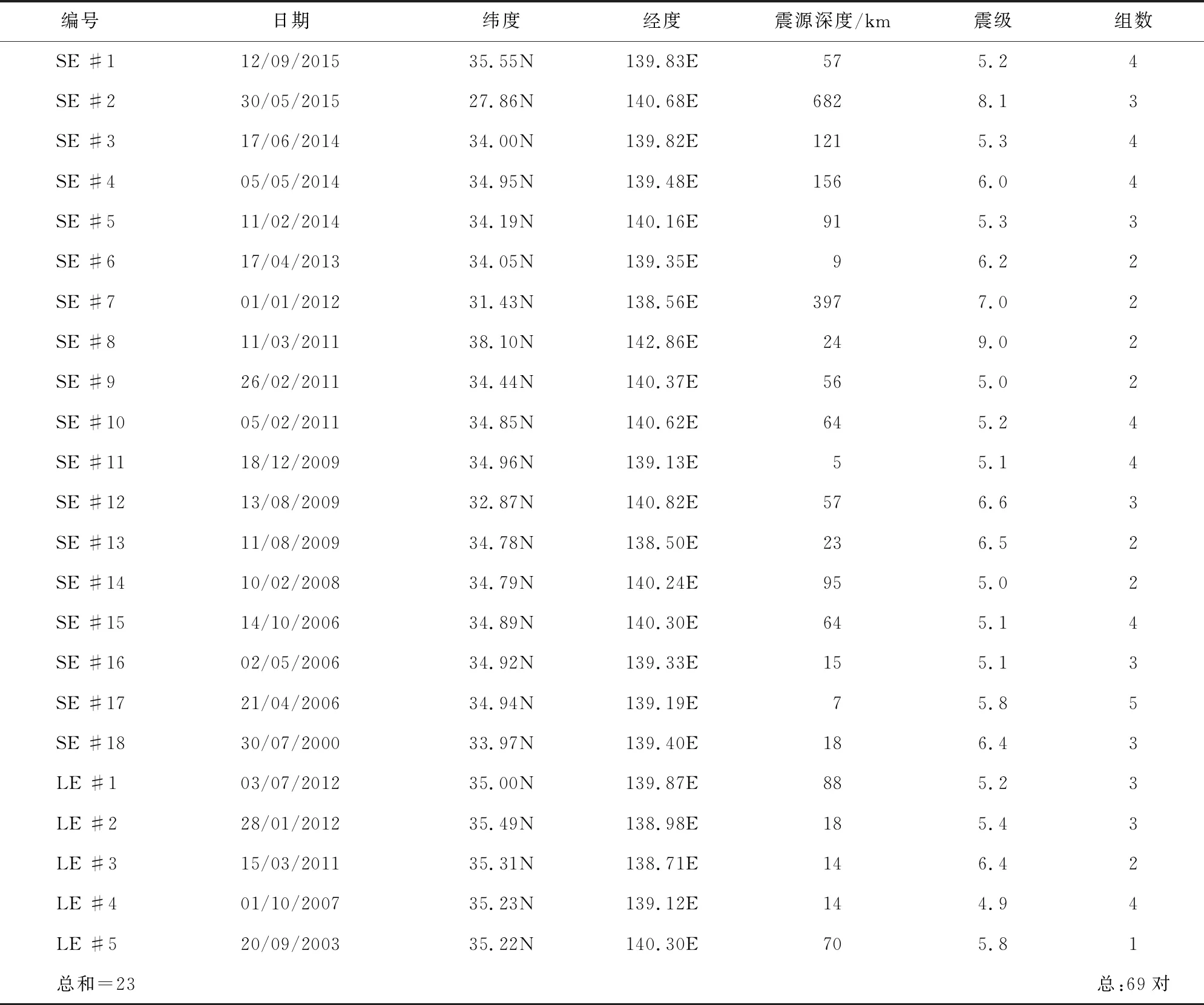
表 2 23场地震相关信息及所选数据对的数量

2 PGA和持时

2.1 PGA

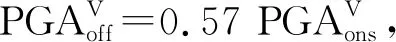
从对比结果来看，海陆不同的场地条件对地震动PGA有很大的影响.海底的场地条件放大了海底地震动的幅值，尤其是水平向地震动.水平地震动对于结构物的抗震设计有着决定性的影响，所以这一发现表明若利用陆地水平地震动直接作为海洋结构得地震荷载输入进行地震响应分析，将会低估地震荷载的作用.

而对于竖向地震动，因其主要由P波构成，而P波可以在海水中传播，由于海水削弱了P波中与海水共振频率处的能量成分[2]，竖向地震动幅值相应地衰减.在海底沉积层放大和海水削弱共同作用的情况下，海陆竖向地震动PGA对比没有明显的规律，见图1(b).

图1 69对海陆地震动PGA的对比(依照震源所在，考虑海底地震与陆发地震)

2.2 持时

持时也是地震动重要特征之一，因其衡量了振动的循环次数，所以关系到结构的线性和非线性响应分析[16-18].有研究表明中等强度但持时很长的地震动可能会比高强度而持时较短的地震动造成的结构非线性响应更大[19].

对于地震动持时的定量化描述方法，目前工程界尚未统一.常用的持时定义方法有绝对持时[20]、等效持时[21]和能量持时[17,22]等.本文采用90%能量持时[17]来确定地震动持续时间，是由于这种方法能够更充分反映地震动的原始特征.该持时定义为地震动能量从总能量的5%累积到95%所经历的时间：

Td=T2-T1，

(1)

(2)

式中：Td表示90%能量持时，T1、T2分别是总能量的5%和95%所对应的时间点.

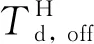
2.3 PGA和能量持时的平均值对比

本文计算了所有69对海陆地震动数据PGA和能量持时Td的统计平均值μ和标准差σ.从结果对比来看，这两个特征参数的统计平均同样验证了上述分析.海底水平地震动PGA平均值为63.56 cm/s2，约是陆地PGA平均值25.73 cm/s2的2.5倍，而海底竖向地震动PGA平均值(12.51 cm/s2)略小于陆地竖向PGA平均值(14.18 cm/s2).另外，海底地震动Td均比陆地地震动Td长，尤其竖向Td平均值(73.90 s)超过陆地Td平均值(33.84 s)的2倍.

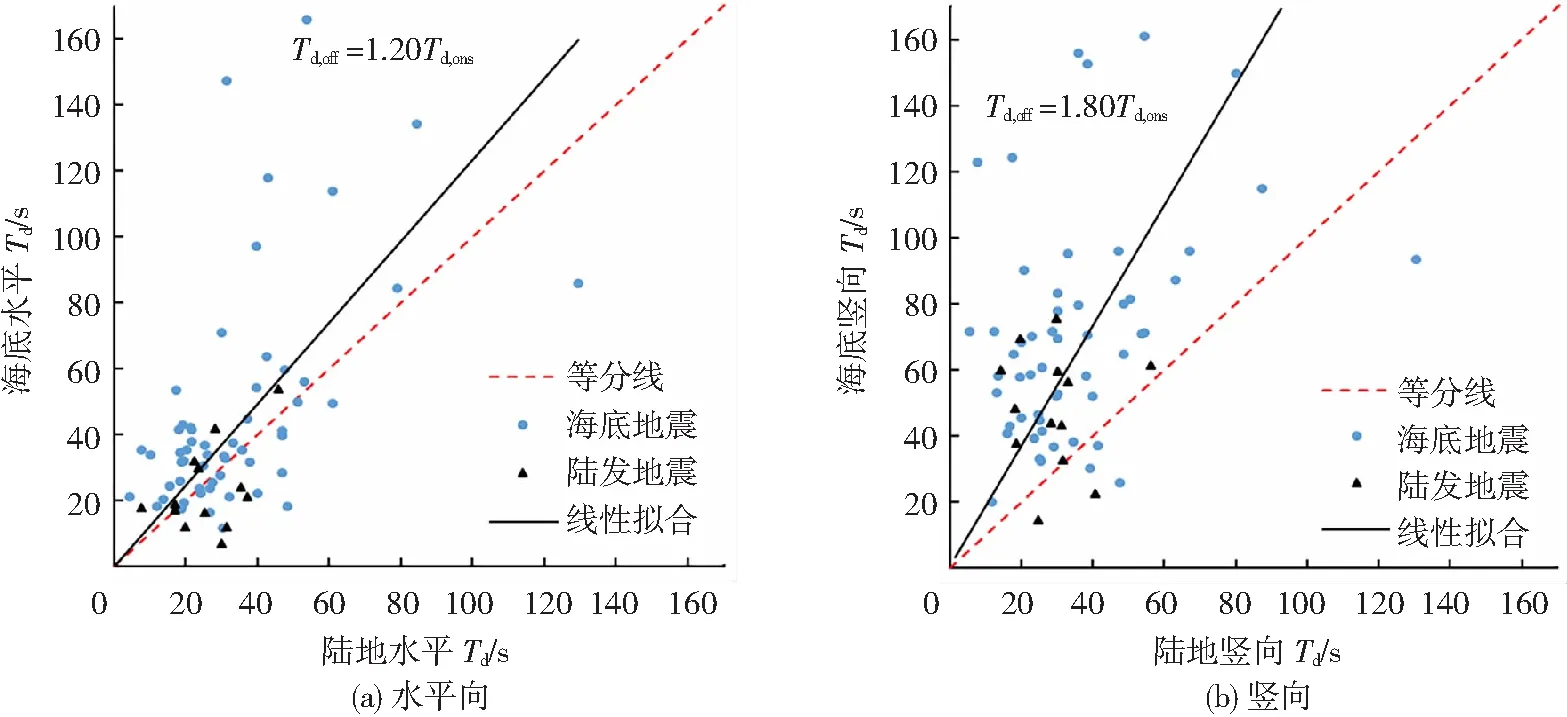
图2 69对海陆地震动的持时Td对比

3 加速度反应谱

地震动的加速度反应谱常被用于结构的频域反应分析[25].加速度放大系数βa则是加速度反应谱与地震动PGA的比值.考虑到对于大部分海洋结构物，如海洋平台和海上风机等，其阻尼主要由结构自身阻尼和水动力阻尼构成，本文选择较为保守的2%阻尼比作为结构受到的总阻尼来进行反应谱计算[26].

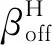
从反应谱的结果可以看出，由于海底沉积土层的影响，地震动的长周期成分被放大，使得反应谱整体向中长周期移动.然而对于竖向地震动而言，由于海水层对高频地震动成分的削弱与压制，处于高频段的加速度反应谱峰值也相应变小，这与文献[1,2,4,27]中的研究结果一致.值得注意的是，很多重要的海洋工程，如跨海大桥、单桩风机等，自振周期都在1 s以上，故而海底场地条件对地震动长周期成分的放大作用会对海洋结构物的地震反应造成不利的影响.

图3 海陆地震动平均加速度放大系数谱

4 时-频分析

4.1 希尔伯特-黄变换(HHT)

由于地震动记录的幅值和频率成分不断随时间变化，在严格意义上是一个非平稳随机过程[28].传统的频域分析方法只适用于平稳随机过程，即幅值和频率不随时间而变化，如傅里叶变换[29]，无法对地震动特性进行精细化研究.为了较好地描述地震动从开始激发到强震段，然后衰减结束的全过程，本文采用希尔伯特-黄变换(HHT)获取HHT谱，进一步研究海陆地震动的能量在时间-频率分布上的差异.HHT变换首先利用经验模态分解方法(EMD)将复杂信号变成一系列符合特定条件的固有模态函数(IMF)，而后对每一个IMF进行希尔伯特变换并得到相应的希尔伯特谱，最后综合所有IMF的希尔伯特谱得到原信号的时频特征谱[30-31].

考虑到所有69对数据呈现相近的结论，受限于篇幅，本文选取了表2 中的SE #17地震中海底台站SR5和陆地台站LR6记录的地震动数据作为代表，详细讨论海陆地震动时-频谱特征.

4.2 HHT谱分析

图4(a)给出了该地震下海陆两个台站东西方向(EW)记录的地震动加速度时程.其中，海底PGA=253.74 cm/s2大于陆地PGA=146.47 cm/s2.图4(b)、(c)分别展示了对应于这两条地震动的HHT时频谱，谱值的大小用颜色的不同显示在时间-频率坐标平面中.从图中可看出，在地面运动触发的早期，无论是海底还是陆地地震动均包含丰富的频率成分，在地面运动后期，很多高频成分逐渐被削弱甚至消失.

对于图4(b)中的陆地水平地震动，HHT谱给出了主要能量的时频域分布，能量主要集中在t=19.74 s到t=20.10 s左右，对应的主要频率成分是从8.40 Hz到12.44 Hz的高频.另外，最大的瞬时能量Einst=151.28 cm2/s4发生在台站记录时刻t=20.05 s，该时间点同样对应于该地震动PGA发生的时刻.该瞬时能量对应的瞬时频率finst=10.61 Hz.由于在地震动频域分析中，人们通常更关注傅里叶谱中卓越频率对结构动态响应的影响，主要是共振等问题.本文利用傅里叶变换同样也计算了各地震动的卓越频率.对于图4(b)中的陆地地震动，其卓越频率fp=9.80 Hz，虽然finst和fp同样对应于最大的能量幅值，但是由于傅里叶变换基于平稳信号，在整个时段对所有频率成分进行平均化处理，使得所获取的卓越频率与利用HHT方法得到的非平稳信号的瞬时频率finst在本质上存在着差别.本文进一步在时程上计算了各地震动PGA所在那个循环的峰-谷周期Tpt，发现该地震动Tpt=0.1 s，或fpt=10 Hz，比卓越频率更接近finst.这一结论适用于其他68对地震动数据.所以考虑到时程的峰-谷周期中包含了PGA，对结构强度影响很大，除了关注卓越频率外，本研究认为还应该在抗震设计中考虑finst或者fpt对结构地震反应的影响.

对于图4(c)中的海底水平地震动，主要能量集中在t=19.83 s到t=20.84 s左右，这与图4(b)中的陆地水平地震动主要能量时段类似，这主要是两个台站震中距相似引起的.不同点是图4(c)对应的主要频率成分来自于1.54 Hz到3.84 Hz的中低频.该海底地震动最大的瞬时能量Einst= 227.81 cm2/s4，比图4(b)陆地地震动大50%，发生于时刻t=20.29 s，相应的瞬时频率finst=2.69 Hz，远低于陆地对照组的瞬时频率.这一结果与反应谱分析类似.希尔伯特谱也反映出，相比于陆地地震动，海底地震动的低频成分被放大.对于该海底地震动，其卓越频率为1.88 Hz，而峰-谷频率为2.33 Hz，后者同样更接近于finst.

从图4(b)、(c)对比还可看出，陆地地震动的能量在大约t=40 s之后即消失，而海底地震动能量的衰减持续到t=100 s之后.这与两条地震动的能量持时长短关系一致，因海底地震动能量持时Td=16.56 s是陆地地震动Td=5.01 s的三倍多.

图4 SE #17中海陆水平地震动HHT谱特征(台站：LR6和SR5)

图5分别给出了该地震下海陆两个台站竖向记录的地震动加速度时程以及HHT谱.和水平向地震动不同的是，海底竖向地震动PGA以及HHT谱中最大能量值小于陆地竖向地震动，而其他HHT谱特征的对比结果与图4中的分析一致，即海底竖向地震动中主要能量所对应的瞬时频率低于陆地竖向地震动，且地震动最大瞬时能量所对应的瞬时频率更接近峰-谷频率，而不是卓越频率.

图5 SE #17中海陆竖向地震动HHT谱特征(台站：LR6和SR5)

5 结 论

1)同一地震下，震中距接近的海底水平地震动PGA通常大于陆地水平地震动PGA.鉴于水平地震动是进行结构抗震设计的关键性动力荷载，工程上在进行海洋结构地震动态响应分析时，如果依然使用陆地水平地震动的PGA结果，很有可能会低估地震动的作用.而对于相应的竖向地震动，总的来说海底竖向地震动PGA比陆地竖向地震动PGA值小.当然，需要注意的是对于水平和竖向PGA的对比结果是针对本研究数据条件而获得的，而影响地震动PGA的因素有很多，对海底地震动PGA今后还应开展更深入广泛的研究.海底地震动的能量持时比陆地地震动更长，尤其是竖向地震动.

2)海底场地条件放大了地震波中长周期成分的能量，使得海底地震动反应谱向中低频偏移.海底水平向地震动反应谱峰值比陆地的大，而海底竖向地震动中高频部分被海水层削弱，其反应谱峰值比陆地的小.使用海底地震动进行海洋工程抗震设计和安全评估是非常重要的.

3)相比于传统的傅里叶变换，希尔伯特-黄变换(HHT)更加适合用来分析非平稳信号的时频特征.海底地震动主要能量成分所对应的频率分布低于陆地地震动.HHT谱中最大瞬时能量所对应的瞬时频率值更接近PGA峰-谷频率，而不是傅里叶谱的卓越频率.因此在地震反应分析时除了考虑卓越频率的影响，还需要考虑PGA峰-谷频率的影响.