考虑阻尼器极限状态的单自由度体系地震响应

骈 超, 钱 江,2

(1.同济大学 结构防灾减灾工程系，上海 200092; 2.土木工程防灾国家重点实验室(同济大学)，上海 200092)

阻尼器在建筑耗能减震方面已得到广泛应用，尤其是液体黏滞阻尼器因其独特优势，在结构工程界成为最受工程师青睐的阻尼器.液体黏滞阻尼器的优点主要有：1)黏滞阻尼器作为附属装置，其刚度为零，所以不影响整个结构的周期和结构设计；2)黏滞阻尼器滞回曲线饱满，能够有效耗散地震输入的能量，减小结构响应；3)在强震和强风荷载下重复使用；4)只要选用合适的内置液体，黏滞阻尼器会有很好的耐久性.

液体黏滞阻尼器最近几年在中国被广泛应用于桥梁、建筑等工程中，但是目前结构设计通常只考虑消能减震构件在规范规定的设防地震作用下正常工作，并没有考虑消能器在实际地震作用下失效的问题.例如中国《建筑抗震设计规范》[1]中规定：消能部件的极限位移(速度)应不小于罕遇地震下消能构件最大位移(速度)的1.2倍，如果是速度相关型的消能构件，还应满足在此极限速度下的承载力要求；同样国外的规范FEMA273[2]中也有类似的规定：在最大地震下，消能器的极限位移(速度)应不小于消能器最大位移(速度)的1.3倍；中国的《建筑消能减震技术规程》[3]关于消能减震结构的性能水准有如下叙述：“当遭受高于本地区抗震设防烈度的罕遇地震影响时，消能构件不应丧失功能，主体结构不致倒塌或发生危及生命的严重破坏.”然而日本3.11地震中位于东北工业大学的一栋钢框架结构首层的8组油阻尼器被完全破坏，油液发生泄漏[4-6]，这是世界范围内首次出现的消能体系破坏案例.随后展开的调查中，也发现许多建筑中阻尼器失效的案例.这些案例表明，阻尼器在遭遇极端地震作用下，是有可能发生失效的.

目前，关于黏滞阻尼器失效的研究并不多.Miyamoto等[7-9]提出了黏滞阻尼器可能的几种极限状态：承载力极限状态、位移极限状态、混合承载力-位移极限状态，并针对黏滞阻尼器基于OpenSEES建立了可以考虑其极限状态的简化模型，并将该模型应用于消能减震结构的非线性动力分析[7]，指出如果将阻尼器的安全系数提高1.3倍，结构倒塌概率将减少至原来的1/2～1/4.Sepehri等[10]针对安装有黏滞阻尼器的消能减震框架提出了一种新的设计方法来减小阻尼器在强震作用下的失效概率.Ataei等[11]指出液体黏滞阻尼器内部硅油泄露将导致其力-位移响应中产生间隙或滞后，并研究了北京银泰中心上安装的液体黏滞阻尼器在内部硅油泄露的情况下，对结构抗震性能的影响.基于Miyamoto等[7-9]提出的黏滞阻尼器在极限状态下的失效模式，宋昊[12]针对一超高层结构研究了黏滞阻尼器的极限状态对其地震响应的影响；王莹[13]研究了黏滞阻尼器漏油和卡动失效对两个实际框架结构抗震性能的影响；朱冬飞[14]针对黏滞阻尼器常见的漏油、间隙、超极限位移和超极限承载力等失效现象建立相应的恢复力模型，并分析其对结构抗震性能的影响; 韩建平等[15]利用OpenSees二次开发得到能模拟黏滞阻尼器位移极限状态和承载力极限状态的Maxwell模型，并将其应用至6层钢框架结构的时程分析中，结果表明不考虑极限状态会高估阻尼器减震性能.针对黏滞阻尼器对单自由度体系地震响应影响的研究较少.

本文根据Miyamoto等[7-9]提出的黏滞阻尼器的3种失效模式，借助Ruaumoko-2D结构动力分析软件创建了能模拟阻尼器极限状态的数值模型，并与Miyamoto等[7-9]提出的模型进行对比，验证该数值模型模拟阻尼器极限状态的可靠性；在多条逐级放大的地震波和正弦波作用下进行时程分析，研究黏滞阻尼器的承载力极限、位移极限对该单自由度体系在不同强度的地震作用下的结构响应的影响，并通过位移时程与阻尼力时程曲线，阐述各极限状态的作用机理.

1 具有极限状态的黏滞阻尼器的数值模型

Miyamoto等[7-9]针对图1的液体黏滞阻尼器提出了其失效的3种极限状态，分别是承载力极限状态、位移极限状态和混合承载力-位移极限状态.其中承载力极限状态是指当阻尼器向外拉伸时如果速度过快会产生较大的阻尼力，导致活塞薄弱区的受拉屈服进而拉裂，或者当阻尼器承受压力作用时，支撑构件发生屈曲从而导致阻尼器失去承载力；位移极限状态是指阻尼器的位移行程超过其可允许的行程范围，造成了活塞与缸筒两端碰撞，缸筒与活塞相对运动速度降为零，因此黏滞阻尼力为零，完全由缸筒进行传力，此时阻尼器本质上变为一个钢支撑；混合极限状态是指当阻尼器的位移行程超过其可允许的行程范围，活塞与油缸两端的接触会导致阻尼器受力急剧上升，受拉时会导致活塞薄弱区屈服进而拉裂，受压时会导致支撑杆屈服或者屈曲失效.

图1 液体黏滞阻尼器构造[7]

具有上述失效极限状态的黏滞阻尼器可通过如下本构关系描述[7]：

(1)

式中：u和F分别代表阻尼器的力和位移；KD、KP和KC分别代表着支撑构件、活塞组件(活塞杆和活塞)和缸筒的刚度；C和α分别为阻尼器的阻尼系数和速度指数；Fmax和umax分别为阻尼器的极限承载力和极限位移.式(1)中的3个公式分别表示阻尼器的正常工作状态、位移极限状态和承载力极限状态.阻尼器正常工作时，是由支撑构件、活塞组件和黏滞阻尼单元串联工作；当达到位移极限状态后，缸筒与活塞相对速度降为零，黏滞阻尼单元退出工作，缸筒替代阻尼单元与支撑构件、活塞组件串联工作；当达到承载力极限状态后，所有单元退出工作.

本文借助Ruaumoko-2D[16]中已有的本构模型，通过图2的方式进行组合来模拟具有上述本构关系的黏滞阻尼器，具体来讲，是由一个黏性单元与一个具有松弛迟滞的双线性(bi-linear with slackness hysteresis)弹簧单元并联，再与一个强度衰减(degrading strength)的弹簧单元串联[16].黏性单元的黏滞性质用下式描述：

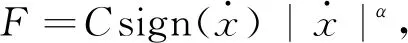
(2)

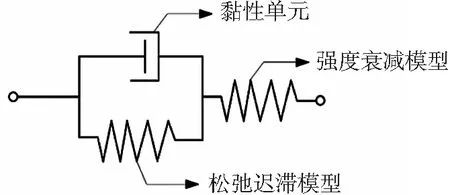
图2 有极限状态的液体黏滞阻尼器的Ruaumoko模型

图3 双线性松弛迟滞模型的本构关系

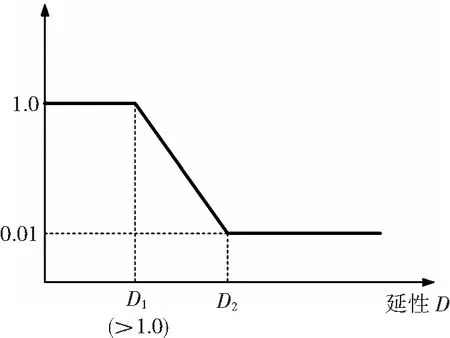
图4 强度与延性的关系

为了验证上述Ruaumoko-2D中建立的考虑极限状态的黏滞阻尼器本构模型的正确性，根据Miyamoto等[7]论文中一个实际的黏滞阻尼器的各主要组成部分的力学参数，分别对阻尼器位移极限状态和承载力极限状态进行数值模拟，并与Miyamoto等[7]的结果进行对比.阻尼器各主要组成部分力学参数分别为：活塞组件的等效刚度为KP=17.25 kN/mm，活塞薄弱区屈服力(极限承载力)为Fmax=1 800 kN，阻尼系数C=148×103N/(mm/s)α，速度指数α=0.3，缸筒行程范围(极限位移)为umax=±100 mm，油缸的刚度KC=175 kN/mm.对比结果见图5、6.

图5 只考虑位移极限状态时阻尼器的响应

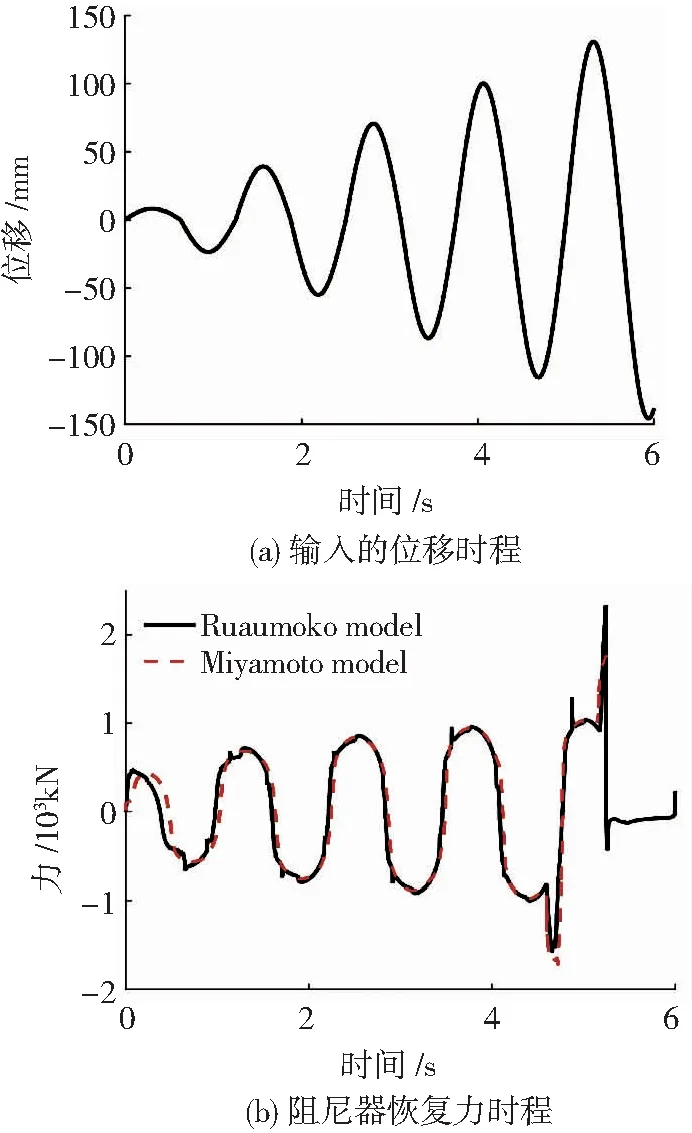
图6 只考虑承载力极限状态时阻尼器的响应

图5(b)为只考虑位移极限状态的黏滞阻尼器在图5(a)所示的振幅逐渐增大的正弦波输入下的时程响应，因为不考虑阻尼器的承载力极限，所以活塞组件的强度值设定为一个较大的数值.图5(b)中实线为本文提出的Ruaumoko模型模拟的结果，虚线为Miyamoto等[7]的结果，二者基本吻合，本文的Ruaumoko模型能够较为准确地模拟出活塞与缸筒两端碰撞时恢复力骤增的效果.

图6(b)为只考虑承载力极限状态时的黏滞阻尼器在图6(a)所示的振幅逐渐增大的正弦波输入下的时程响应，因为不考虑阻尼器的位移极限，所以活塞的行程范围被定义为一个较大的范围，来保证活塞不会与缸筒发生碰撞.由图6可见，本文提出Ruaumoko模型模拟的结果与Miyamoto等[7]的结果非常接近，可以准确模拟出当阻尼器受力超过承载力极限时，恢复力快速降为零，阻尼器退出工作.

2 阻尼器极限状态对单自由度体系地震响应的影响

以下分析黏滞阻尼器的极限状态参数(极限承载力和极限位移)分别对单自由度体系在地震波和正弦波作用下地震响应的影响.该单自由度体系由具有理想弹塑性本构的主结构、具有3种极限状态的黏滞阻尼器次结构和质点M构成，见图7.单自由度体系能够代表实际结构的宏观响应，提高计算效率，便于参数分析，同时也能够排除结构刚度、强度分布和阻尼器分布等因素的干扰.因此将层数分别为2层和10层的钢筋混凝土框架的结构等效为两个单自由度体系，分别代表短周期结构和中长周期结构.两个等效单自由度体系的力学参数见表1.

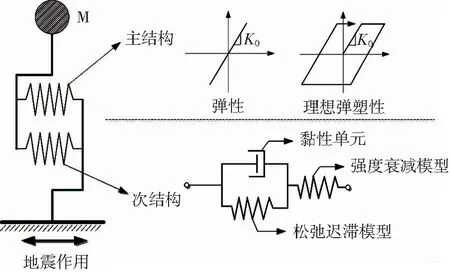
图7 单自由度体系

分别选用3条振幅为0.14g(g为重力加速度), 频率为0.28、0.65、2.27 Hz的正弦波和4条分别代表4类场地的地震波作为地震动输入，逐级放大地震作用，使得输入的地震动的峰值速度(PGV)在0～150 cm/s区间内变化.4条地震波为ATC-63[17]所推荐，借用SeismoMatch反应谱匹配工具，分别按照中国抗震规范规定的抗震设防烈度为9度的多遇地震(αmax=0.32)、设计地震分组为第一组对应的4类场地的反应谱进行匹配，处理后的4条地震波的加速度反应谱与各自对应的规范反应谱见图8.

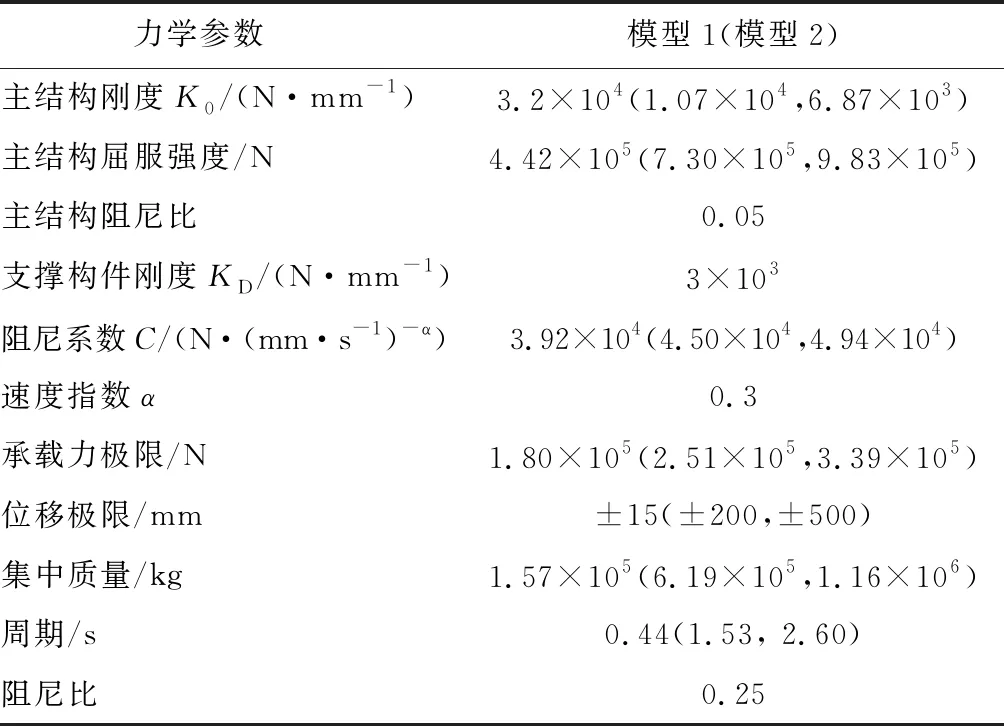
表1 模型力学参数

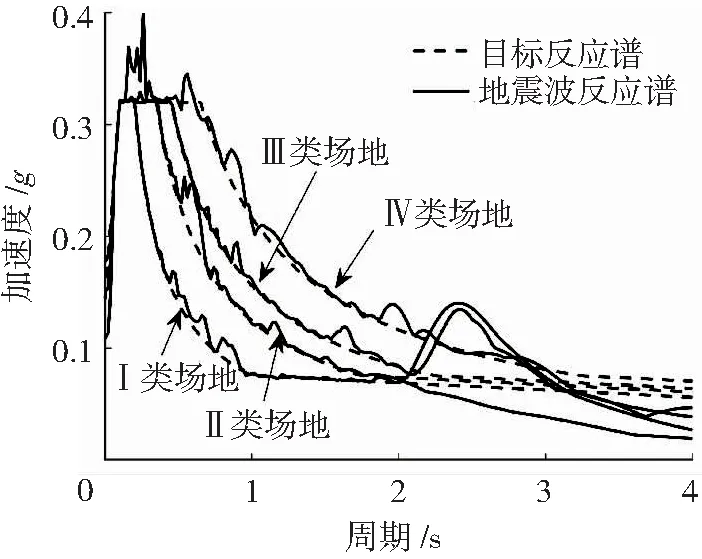
图8 输入的地震波反应谱与规范谱

2.1 承载力极限状态

单自由度体系在逐级放大的地震波和正弦波作用下的响应结果见图9、10.整体上看承载力极限对结构地震波响应起放大作用.从图10可看出，当正弦波的频率与结构自振周期一致时，阻尼器极限状态对结构的影响会明显增大.为了考虑不同极限承载力对单自由度体系响应的影响，将表1对应的极限承载力减小，在逐级放大的地震波和正弦波作用下再次进行分析，结果见图11、12，整体上的位移比要明显大于图9、10中的位移比，而且临界峰值速度也明显降低；位移比随着地震动峰值速度先突增后减小，而且位移比最终衰减到接近1，也就是说，当地震动峰值速度在大于临界峰值速度、并且处在临界峰值速度附近时，阻尼器极限状态对结构最大位移响应的放大作用最为明显，当地震动峰值速度较大时，不管是否考虑阻尼器的承载力极限状态，对最终结构最大位移响应都影响不大.

图9 考虑承载力极限的单自由度体系地震波响应

图10 考虑承载力极限的单自由度体系正弦波响应

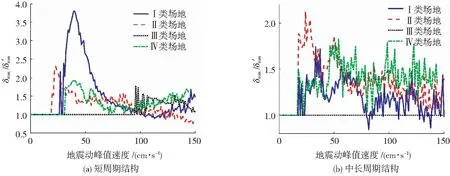
图11 承载力极限降低后考虑承载力极限的单自由度体系地震波响应

为了直观地体现阻尼器的承载力极限对单自由度体系地震响应的影响，图13分别列举了只考虑阻尼器承载力极限状态两个单自由度体系在峰值地面加速度为0.65g的II类场地对应的地震波输入下结构的位移和相应的阻尼力的时程曲线.从图12(b)可见当阻尼器所受的力达到极限承载力时，阻尼力快速降为零，这一时刻就代表着阻尼器活塞薄弱区受拉屈服进而拉裂导致阻尼器失效，而在失效前的阻尼力时程曲线与不考虑承载力极限的阻尼力时程曲线完全重合；图13(a)的阻尼器因为没有达到受拉承载力极限，所以没有失效，因此两条曲线重合.

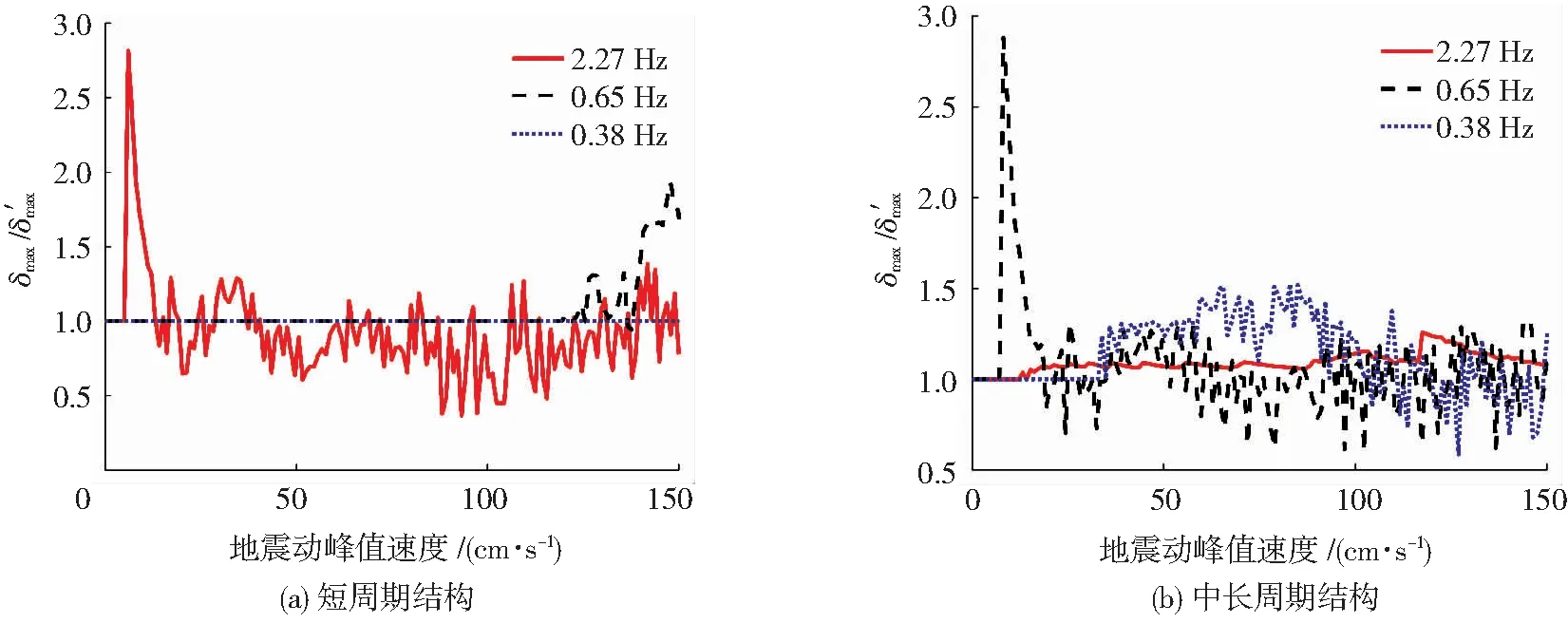
图12 承载力极限降低后考虑承载力极限的单自由度体系正弦波响应

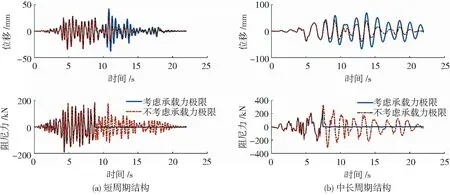
图13 考虑承载力极限的单自由度体系位移和阻尼力的时程曲线

2.2 位移极限对单自由度体系地震响应的影响

本小节只考虑黏滞阻尼器达到极限位移后失效对结构响应的影响，研究位移比与地震动峰值速度之间的关系，图14、15为逐级增大地震波和正弦波作用下单自由度体系的位移比与峰值速度的关系曲线.结果表明，单自由度体系位移比与峰值速度的关系曲线没有明显的规律性.图16列举了考虑阻尼器位移极限状态的单自由度体系在峰值地面加速度为0.65g的II类场地对应的地震波输入下结构的位移和相应的阻尼力的时程曲线，在达到阻尼器位移极限之前，考虑极限状态和不考虑极限状态对应的位移时程曲线是相互重合的，从阻尼力时程曲线可看出，在达到位移极限时阻尼力会有明显突增.

图14 考虑位移极限的单自由度体系地震波响应

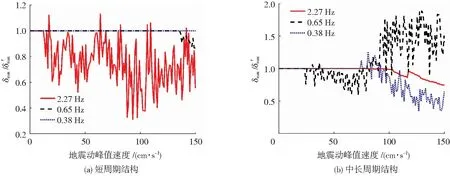
图15 考虑位移极限的单自由度体系正弦波响应

图16 考虑位移极限的单自由度体系位移和阻尼力的时程曲线

2.3 混合极限对单自由度体系地震响应的影响

当阻尼器在达到位移极限之前，先达到承载力极限，则本质上与只考虑承载力极限时是完全相同的.本节期待达到的失效效果是当阻尼器的位移行程超过其可允许的行程范围，活塞与油缸两端的接触会导致阻尼器受力急剧上升，受拉时阻尼器因达到极限承载力而失效.为了实现先位移极限后承载力极限的失效效果，人为将表1中的位移极限减半.图17、18为逐级增大地震波和正弦波作用下单自由度体系的位移比与峰值速度的关系曲线.从图17可见混合极限对应的位移比随着地震动峰值速度的变化规律与承载力极限对应的变化规律类似，但是位移比整体上要比2.1节中承载力极限对应的位移比更大，先突增后下降的变化规律更为明显，这是因为位移极限导致阻尼器更快达到极限承载力，阻尼器耗能减小，位移响应增大，进而导致位移比增大.但是图18表明，并没有上述规律，初步推测是由于阻尼器承载力极限相对较大.为了验证这一推测，人为将对应的极限承载力减小，在逐级放大的正弦波作用下再次进行分析，结果见图19，当阻尼器极限承载力减小后，位移比随着地震动峰值速度的变化规律与2.1节的结论相类似.

图20分别列举了同时考虑阻尼器承载力极限和位移极限状态(混合极限状态)的两个单自由度体系在峰值地面加速度为0.65g的II类场地对应的地震波输入下结构的位移和相应的阻尼力的时程曲线.从图20 (a) 可见，在阻尼器失效前，是否考虑极限状态，所得阻尼力时程不完全重合，这与图13承载力极限状态对应的时程曲线的特征并不一致，这说明，在达到极限承载力之前，阻尼器先达到位移极限状态，造成两条曲线的不重合；图20(b)阻尼力没有最终降为零，说明阻尼器并未失效，但是两条曲线不重合，说明达到位移极限但没有达到承载力极限.

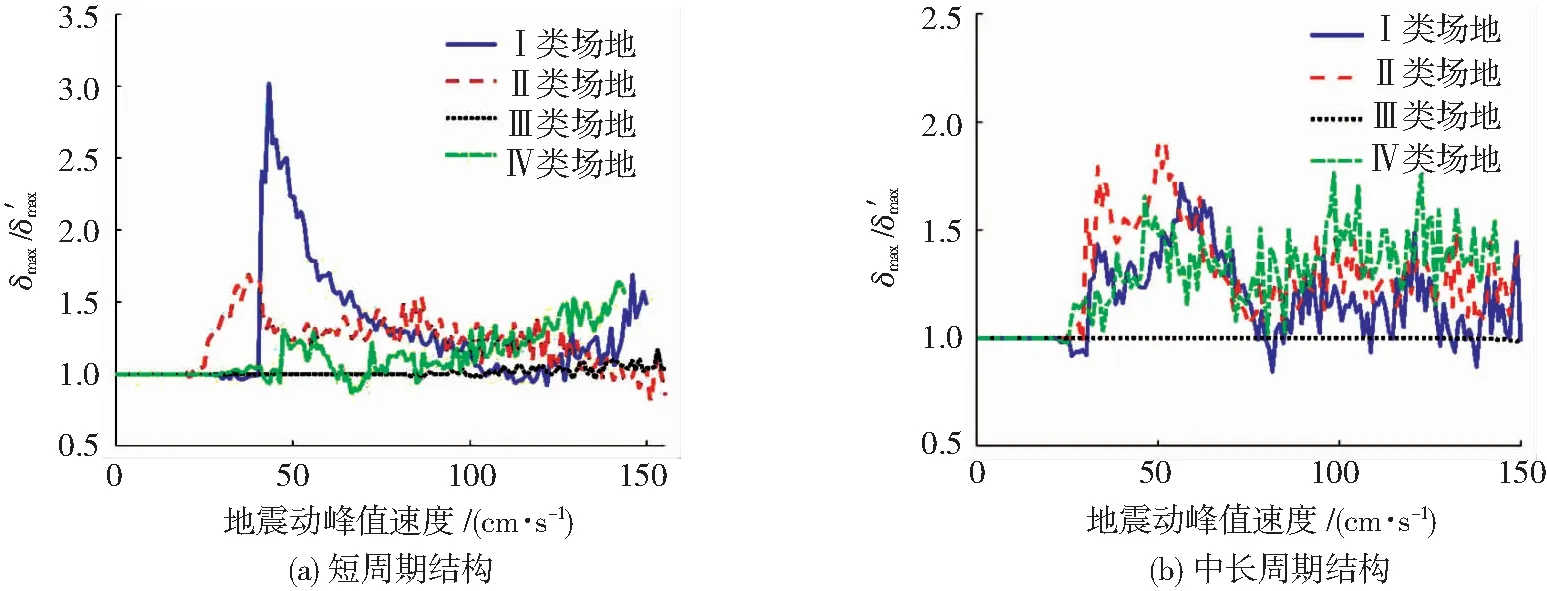
图17 考虑混合极限的单自由度体系地震波响应

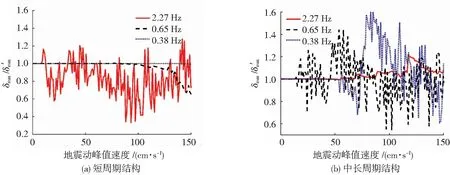
图18 考虑混合极限的单自由度体系正弦波响应

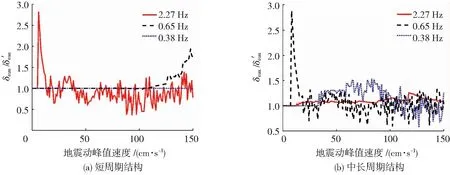
图19 承载力极限降低后考虑混合极限的单自由度体系正弦波响应

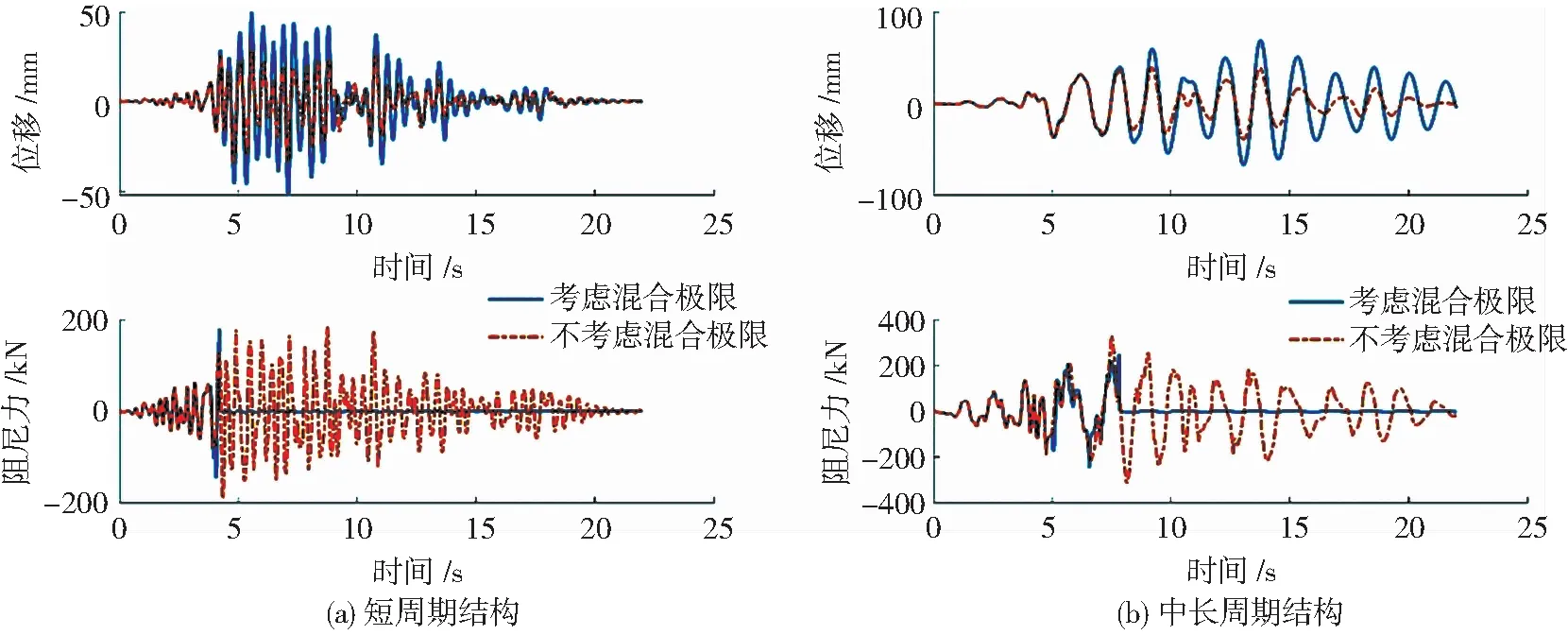
图20 考虑混合极限的单自由度体系位移和阻尼力的时程曲线

3 结 论

1)在软件Ruaumoko-2D中引入Miyamoto 等提出的黏滞阻尼器模型能够较为准确地模拟黏滞阻尼器的3种极限状态.

2)在考虑阻尼器承载力极限状态或混合极限状态情况下，在逐级放大多条地震波和正弦波作用下，随着输入地震波的峰值速度的增加，达到临界峰值速度时，位移比会迅速攀升至最大值然后开始迅速衰减，衰减速度越来越慢.极限承载力越小，极限位移越小，先突增后减小的变化规律越明显.

3)提高黏滞阻尼器承载力极限和位移极限，能够有效地降低位移比，提高临界峰值速度，整体上对于降低结构位移响应有着重要作用.