巧用图像本质破解三角函数参数取值范围

福建省泉州市第七中学 (362000) 赖呈杰 林景芳

函数y=Asin(ωx+φ)(A>0,ω>0)的图像和性质是三角函数考查的重点内容之一，它涵盖了单调性、对称性、最值、零点等内容，其中关于ω范围的问题在近年来的全国高考试卷和各地的模拟卷中屡屡出现，该问题也是学生感到棘手的问题之一.笔者认为，处理ω范围问题只需紧抓函数的图像本质，就能轻松破解，本文就几种常见的类型进行剖析.

类型一 与单调性有关的问题

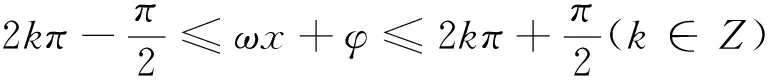
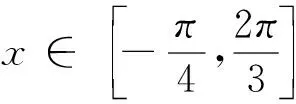
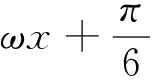
类型二 与最值有关的问题

评注：最值问题通常要求出最值点，让最值点落在指定区间，再结合函数图像特点加以解决，特别要注意到函数在单调开区间内无最值.

类型三 与对称性、零点有关的问题

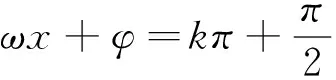
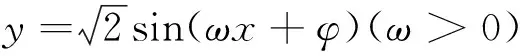
A.1B.2C.3D.4

结合正弦函数的图像，有以下几种情形：

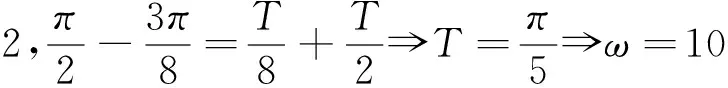
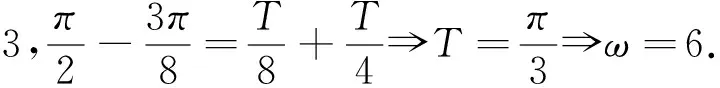
因此ω=2或ω=6.

A.11B.9C.7D.5