基于耦合协调度的大理河流域径流和输沙关系分析

2020-07-22任宗萍李占斌徐国策张铁钢杨媛媛

农业工程学报 2020年11期

贾路，任宗萍※，李占斌，李鹏，徐国策，张铁钢，杨媛媛

（1. 西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048；2. 旱区生态水文与灾害防治国家林业和草原局重点实验室，西安 710048；3. 水利部牧区水利科学研究所，呼和浩特010020）

0 引言

黄河是中华民族的母亲河，随着气候变化与人来活动的影响，黄河流域生态环境状况及自然条件发生了巨大变化，黄河流域的健康和高质量成为一项重大国家战略，黄河流域的发展关系着流域内人民的生产和生活的长远发展[1-2]。黄河中游地区占据了黄河流域的大部分面积，该区域位于世界水土流失最为严重的地区之一-黄土高原，因此治理黄河流域的水沙变化问题一直是治黄工作的核心问题[3-4]。自20 世纪50 年代开始，中国在黄土高原地区实施了大规模的水土保持工程建设，特别是淤地坝工程的建设，有效地拦截了黄土高原地区产生的泥沙，调节了径流，阻止泥沙进入黄河，黄河径流和泥沙显著减少[5]。同时，近几十年全球气候发生显著变化，全球变暖的趋势日益加剧，极端事件频发，已经受到国际社会的普遍关注，气候变化进一步加剧黄河流域水资源的供需矛盾[6-7]。气候变化有可能会加速全球水文循环，这对水沙关系的变化将产生非常重大的影响。研究气候变化条件和人类活动作用下水文过程和水沙变化的状况是目前水文学和水土保持的热点问题之一。

径流和泥沙作为流域极具重要价值的资源，在流域社会、经济和生态环节中扮演着重要的角色。许多研究调查了气候变化和人类活动影响下的径流和输沙的变化特征。曹丽娟等[8]对未来气候变化条件下黄河和长江流域极端径流影响预估进行了研究。欧阳潮波等[9]对60 a 来黄河河龙区间水沙变化特征及人类活动的影响进行了评价。高海东等分析了2000—2017 年河龙区间输沙量锐减的原因[10]。尽管关于径流和输沙对气候变化和人类活动时空变化响应及归因分析的研究已经被进行了研究，并取得了很多的研究成果。但是有一个事实是至关重要的，由于过去的研究大多数是基于单变量角度对流域水文变量间的关系包括水沙关系进行的研究，所以这成为造成识别的变量之间的变化存在巨大的差异[11-12]。在自然界中，地表水、大气、植被、土壤和地下水等环境要素之间存在复杂的相互作用[13]，使用单变量的分析方法可以让事情变得简单、便捷。然而，单变量的分析方法只关注了单个变量的变化（例如径流或输沙），这与现实差别较大，不能完全揭示对气候变化和人类活动的水沙响应。因此，有必要基于多变量的视角研究径流和输沙的变化特征。

大理河流域作为黄河的二级支流[14]，位于中国典型的干旱和半干旱区域。同时，由于大理河流域地处中国黄土高原地区，地形破碎，沟壑区密度大，水土流失比较严重，耕地资源和水资源非常有限。这一情况对该区域工农业发展来说，是十分不利的。众所周知，大理河流域的径流呈现显著下降[15]，这使得当地水资源的供需矛盾进一步加剧，同时伴随着严重的泥沙问题。在过去的许多时间，关于大理河流域的气候变化和人类活动影响下的径流变化和输沙变化的研究已经取得了显著的成果。但是，大部分研究重视探索造成径流变化和输沙变化等单个变量变化的气候变化和人类活动因素，关于径流和输沙之间关系的研究还需要不断探索和深入研究。径流和输沙之间的水沙关系作为流域物质循环中至关重要的环节，二者之间的关系具有紧密的联系，这是水土保持研究关注的重点问题之一[16]。一直以来研究径流输沙之间的关系对于优化流域水土流失治理工作，评估流域水土保持效益都是必要的。一旦流域径流和输沙和之间的关系存在突变，这意味着流域的水文机制和水沙关系已经发生了改变，对于工程设计工作来说也必须进行改变，才能有效地兴利除害。因此，基于多变量视角对大理河流域径流和输沙的变化关系进行探索至关重要，对在气候变化和人类活动的巨大影响条件下指导当地进行水资源规划和水土保持具有重要意义。

本文通过Mann-Kendall 检验研究径流输沙的变化趋势，基于耦合协调度理论和Pettitt 检验方法构建流域径流和输沙之间关系的突变点的识别方法并进行诊断，并通过Copula 方法进行了验证，探讨了造成大理河流域径流和输沙关系变化的可能驱动因素。研究有助于进一步深化对大理河流域水沙关系变化的认识，为大理河流域水土保持工作开展提供一定的科学依据。

1 材料与方法

1.1 研究区概况

大理河流域位于中国黄河流域中游（109°14′～110°13′E，37°30′～37°56′N），绥德水文站为流域出口水文站[17]，如图1 所示。大理河为无定河的第二大支流，起源于靖边县白于山东测的五台山，流经横山县、子洲县、绥德县，在绥德县东北部注入无定河。大理河全长159.9 km，流域面积3 904.24 km2，比降3.16‰，流域地面坡度较大，大部分在15°以上，主要支流有小理河、岔巴沟、驼耳巷沟等。流域西高东低，地形起伏较大，海拔796～1 744 m。流域主要土壤类型为黄绵土和新积土，属于黄土峁状丘陵沟壑区。流域内坡长多大于200 m，沟谷切割深度多大于50 m，使得流域形成了许多坡陡沟深的小流域。流域土壤侵蚀为严重，经过几十年的水土保持综合治理，水土流失量明显下降。

1.2 数据来源

本文所使用的径流和输沙数据来源于黄河水文年鉴，时间序列为1960—2015 年。降水数据是来源于国家地球系统科学数据中心的栅格降水量数据（http：//loess.geodata.cn），时间序列为1960—2017 年，空间分辨率为1 km×1 km，时间分辨率为月，该数据使用全国496 个独立气象观测点数据进行了验证，验证结果可信，该数据可以准确的反映全流域降水的变化分布情况。淤地坝数据来源于2011 年第一次全国水利普查。中国年度植被指数（NDVI）空间分布数据集是基于连续时间序列的 SPOT/VEGETATION NDVI 卫星遥感数据（http：//www.resdc.cn/data.aspx?DATAID=257），采用最大值合成法生成的1998 年以来的年度植被指数数据集。该数据集有效反映了全国各地区在空间和时间尺度上的植被覆盖分布和变化状况，对植被变化状况监测、植被资源合理利用和其他生态环境相关领域的研究有十分重要的参考意义。

图1 陕西省大理河流域地理位置 Fig.1 Location of the Dali River Basin, Shaanxi province

1.3 研究方法

1.3.1 Mann-Kendall 检验

Mann-Kendall（M-K）检验[18]是一种非参数的判断数据序列变化趋势的分析方法，常被广泛使用在气象和水文序列的趋势检验中，本文采用Mann-Kendall 检验捕捉径流量、输沙量、NDVI 以及其他变量的变化趋势。

1.3.2 耦合协调理论

耦合最早是作为一个物理学的概念，指2 个或2 个以上系统或运动形式通过各种相互作用而彼此影响的现象[19]。随着研究的发展，耦合概念被逐步引入到生态学领域中，并被广泛使用[20]。多个系统相互作用耦合度模型可以用一下模型表示[21]

式中Cn为n 元系统的耦合度；u1…un分别为第一个子系统到第n 个子系统对总系统有序度的贡献，计算方法如下

式中ui为第i 个子系统对总系统有序度的贡献；uij为第i个子系统中第j 个指标的归一化值；wij为第i 个子系统中第j 个指标的权重，每个子系统中指标的权重计算使用熵权法进行计算。

在计算每个子系统的熵权时，必须先进行归一化处理，这里采用最大最小值法进行归一化处理：

当uij为数值越大对系统越好时（正向归一化）

当uij为数值越小对系统越好时（负向归一化）

式中xij为子系统第i 个指标的第j 个时序的值。

根据多元系统的耦合度模型，容易得到径流和输沙2个子系统之间的耦合度模型，可以表示成以下形式

式中C 为径流输沙二元系统的耦合度。在本研究中径流和输沙子系统的指标为12 个月的月径流量和月输沙量，每个指标的权重计算采用熵权法，假定径流越大对系统越好，输沙越少对系统越好。

由于耦合度指标在有些情况下却很难反映出子系统整体“功效”与“协同”效应，耦合度各子系统指标的上下限取自各指标的极值，而极值存在动态、不平衡的特性，单纯依靠耦合度判别有可能产生误导。为此，进一步采用耦合协调度模型来评判径流子系统和输沙系统交互耦合的协调程度，计算公式如下

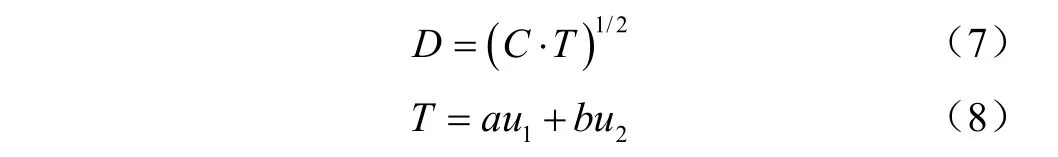
式中D 为耦合协调度；C 为耦合度；T 为径流子系统与输沙子系统的综合调和指数，它反映径流子系统与输沙子系统的整体协同效应或贡献；a、b 为待定系数，实际中常常认为两个子系统的重要性相同[21]，所以a=b=0.5。

1.3.3 边际分布函数与Copula 函数

边际分布函数[22]是统计学中一种描述单变量与其概率分布的函数，不同的分布函数可以刻画不同的变量的特征。在本研究中，指数分布函数、耿贝尔分布函数、皮尔逊三型分布函数和广义极值分布函数被使用来拟合径流和输沙数据，同时通过计算4 种理论分布函数累积概率和经验累积概率的R2来优选出最优的理论分布函数。

Copula 函数是一种可以用来描述多个变量联合分布的一种连接函数[22]，由于它可以连接任何2 个边际分布函数，因此使用起来十分方便。Copula 函数具有很多家族，其中阿基米德家族Copula 函数因为具有较少的参数，所以被广泛使用。本研究中通过AIC 准则，从阿基米德家族Copula 函数的Frank Copula、Gumbel Copula 和Clayton Copula 3 种Copula 这种选出最优的Copula 来连接大理河流域径流和输沙的最优边际分布函数，构建出最优的径流输沙最优Copula 分布函数。

1.3.4 Pettitt 突变点检验

Pettitt 检验法[23]采用Mann-Whitney 中Ut,n值检验同一总体中2 个样本X1,…,Xt和Xt+1,…,XN，Pettitt 检验的零假设为没有变化点，当|Ut,n|取最大值时对应的Xt被认为是可能的突变点。当P≤0.05 时认为数据中存在均值变异点。其显著性水平可由下式计算

当P≤0.05 时认为数据中存在均值变异点。

2 结果与分析

2.1 径流和输沙变化趋势

大理河流域1960—2015 年各月及年径流量和输沙量的变化趋势计算结果如表1 中所示。径流在3、4、5、8、10、11 月以及年尺度均呈现显著的下降趋势，其中3、4、10 月以及年尺度的M-K 统计量绝对值较大，表明径流下降幅度较大，1 月的径流呈现不显著的增加趋势，其他月份的径流呈现不显著的下降趋势。在1960—2015年间，各月输沙以及年尺度输沙均呈现显著的下降趋势，相比同一月份的径流变化趋势而言，输沙的M-K 统计量绝对值均高于径流，说明输沙的下降幅度更大。在1960—2015 年间大理河流域的径流与输沙变化均存在明显的下降趋势，但径流与输沙的变化幅度呈现出不协调的特点。

表1 1960—2015 年大理河流域径流量和输沙量变化趋势 Table 1 Trends of runoff and sediment load in the Dali River Basin from 1960 to 2015

2.2 径流输沙关系变异诊断

2.2.1 径流子系统与输沙子系统的指标变化

本研究中认为径流越大对系统越好，输沙越少对系统越好，选取每年12 个月的径流量和输沙量分别作为两个子系统的构成指标，对每个指标即每个月的径流量和输沙量进行了归一化处理，使用熵权法计算每个指标的权重，如表2。

表2 的结果显示，1960—2015 年间6 月的径流量在一年中权重最大，11 月的径流量权重最小，4、5、7、8、9、10 月的径流量权重较大。在1960—2015 年间，输沙量在8 月的权重最大，2 月和7 月的权重较大。径流的权重值变异系数为0.58，输沙的权重值变异系数为0.51，径流量年分配权重比输沙更为不稳定。

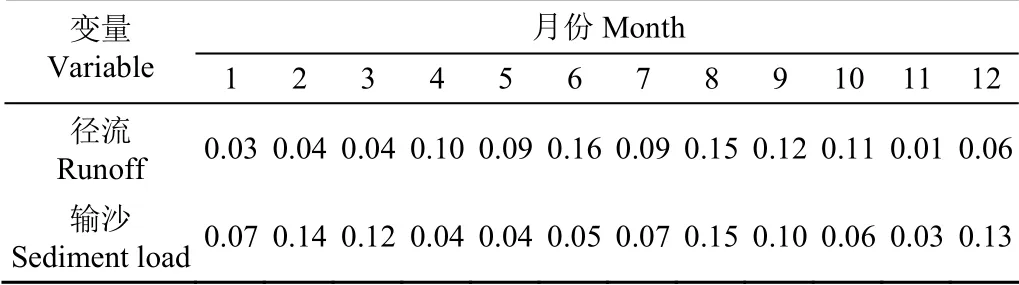
表2 1960—2015 年大理河流域径流量和输沙量权重 Table 2 Weights of runoff and sediment load in the Dali River Basin from 1960 to 2015

2.2.2 径流和输沙耦合协调度的变化趋势与突变点

根据耦合协调度理论计算了大理河流域径流子系统和输沙子系统的耦合协调度，并通过Pettitt 检验方法识别了径流输沙耦合协调度的突变点年份，它反映了大理河流域径流和输沙之间关系的变异特征（图2）。

图2a所示的是1960—2015年间大理河径流输沙耦合协调度的时间序列图，最大值为0.75，最小值为0.42，根据M-K 趋势检验结果表明径流输沙耦合协调度呈现显著下降趋势，说明大理河流域径流输沙关系协调程度不断下降。图2b 表明大理河流域径流输沙耦合协调度的突变点为1996 年，在1996 年径流和输沙之间存在显著突变点，通过对突变点前后的2 个耦合协调度的子序列进一步进行Pettitt 检验，发现不存在显著突变点，这表明大理河流域径流和输沙关系只在1996 年存在明显的不同。

2.2.3 基于Copula 函数的径流输沙突变点验证分析

为了对基于耦合协调度理论识别的径流和输沙关系变异点诊断结果进行验证，本研究采样Copula 函数构建了径流和输沙之间的最优联合分布累积概率，并识别了突变点（图3）。

图2 1960—2015 年大理河流域径流量和输沙量耦合协调度变化及其突变点 Fig.2 Changes of coupling coordination of runoff and sediment load and its change-points in the Dali River Basin from 1960 to 2015

图3 1960—2015 年大理河流域径流和输沙之间的最优联合分布累积概率 Fig.3 Cumulative probability of optimal Copula joint distribution of runoff and sediment load in Dali River Basin from 1960 to 2015

指数分布函数、耿贝尔分布函数、皮尔逊三型分布函数和广义极值分布函数等4 种理论分布函数被使用来拟合大理河流域1960—2015 年的年径流和年输沙数据，通过K-S 检验分别检验了年径流和年输沙数据，发现年径流和年输沙都通过了K-S 检验，这表明4 中理论分布函数都可以用来描述年径流和年输沙，同时使用线性矩法估计了4 种理论分布函数的参数，分别通过计算年径流和年输沙的经验累计概率与4 种理论分布函数的累积概率之间的R2，根据R2最大原则选取该分布函数为最优的分布函数。结果表明，大理河流域1960—2015 年年径流的最优分布函数为皮尔逊三型分布，年输沙的最优分布函数为指数分布。图3a、3b 分别为大理河流域1960—2015 年年径流量、输沙量的最优分布函数累计概率与经验累积概率的时间序列图。基于AIC 准则，从阿基米德家族Copula 函数的Frank Copula、Gumbel Copula 和Clayton Copula 三种Copula 中选出Frank Copula 作为最优的Copula 来连接大理河流域径流和输沙的最优边际分布函数，计算出来径流和输沙之间的联合分布函数累积概率（图3c）。根据M-K 趋势检验对径流和输沙之间的联合分布函数累积概率的分析可知，大理河流域径流和输沙之间的联合分布函数累积概率呈现显著下降趋势，Pettitt 检验对径流和输沙之间的联合分布函数累积概率分析结果表明大理河流域径流和输沙之间关系在1996 年存在显著突变点（图3d）。2 种径流输沙关系突变点的诊断方法表明，基于耦合协调度的径流输沙关系变异诊断方法可以准确的识别出径流输沙的关系突变点。

2.3 变异前后径流输沙变化特征分析

2.3.1 径流输沙变化特征分析

对比年径流量-年输沙量关系突变点前后，径流与输沙的年内和年际的变化特征，可以发现大理河流域1960—1996 年年径流量为1.50 亿m3和1996—2015 年径流量为1.08 亿m3，1996—2015 年期间相比1960—1996 年期间径流量减少27.92%，减少幅度较小。1960—1996 年年输沙量为0.43 亿t 和1996—2015 年输沙量为0.17 亿t，1996—2015 年期间相比1960—1996 年期间输沙量减少57.11%，输沙的减少幅度比径流的减少幅度高29.19 个百分点。1996—2015 年各月径流量、输沙量与1960 —1996 年各月径流量、输沙量相比较发现，除了12月径流量相比突变前有所增加，其余各月径流量均在减少；输沙量在12 个月中均发生了明显的减少现象，特别是在8 月份，径流和输沙的减少量最大（图4）。

图4 突变点前后径流量和输沙量年内分配 Fig.4 Annual distribution of runoff and sediment load before and after the change-point

2.3.2 径流输沙关系变异

径流和输沙关系突变点前后径流和输沙的散点图，如图5。由径流和输沙关系突变点前的径流和输沙相关图（图5a）可以看出，径流输沙关系可以被线性回归方程描述，径流和输沙的决定系数R2为0.867 3（P<0.05），在统计学意义上，决定系数R2表示自变量可以解释因变量的程度，因此，在1996 年之前大理河径流对输沙贡献程度高达86.73%，单位的径流输沙能力较强。图5b 突变点后大理河的径流和输沙相关图表明，在1996—2015 年径流输沙关系也可以被线性回归方程很好的描述，径流和输沙的决定系数R2为0.823 1（P<0.05），在1996 年后大理河径流对输沙贡献程度降低到82.31%，下降幅度为5.10%，单位的径流输沙能力降低。

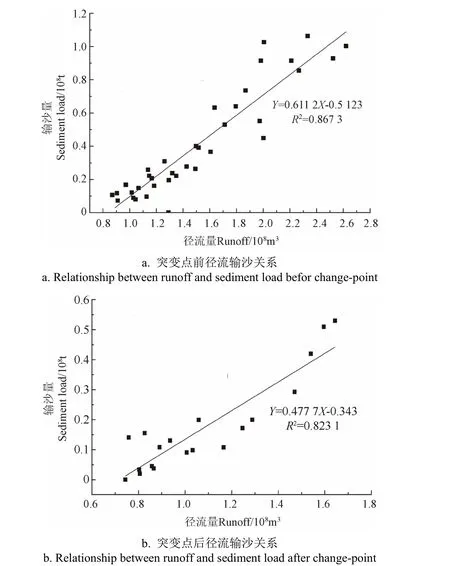
图5 大理河流域突变点前后径流输沙关系 Fig.5 Relationship between runoff and sediment load before and after the change-point in Dali River Basin

2.4 气候变化和人类活动对径流输沙变化的贡献率

对径流和输沙变化影响的主要驱动因素包括气候因素和下垫面因素[24]。本研究使用双累积曲线分析两者对大理河流域1960—2015 年径流和输沙变化的影响。

如图6 所示为1960—2015 年大理河流域年降水量和年径流量双累积曲线（图6a）、年降水量和年输沙量（图 6b）。从图6a 中可以看出，大理河流域年降水量和年径流量之间存在较弱的非一致性。图6b 表明，大理河流域年降水量和年输沙量之间存在明显的非一致性关系。结合图6，将降水和径流、输沙关系划分为3 个时段，分别为1960—1971、1972—1996、1997—2015 年。将1960—1971 作为基准期，认为该时期降水径流关系和降水输沙关系未发生变化，具有一致性，定量分析气候变化和人类会动对径流和输沙变化的贡献率，如表3 所示。在1972—1996、1997—2015 年2 个时期人类活动对径流和输沙减少的贡献率均远远高于气候变化的影响，特别是在1997—2015 年时期，气候变化对径流和输沙变化表现出增加的作用，这表明下垫面的人类活动是导致大理河流域径流和泥沙减少的主要驱动力，这与刘晓燕等[25-26]人的研究结果一致。

表3 气候变化和人类活动对大理河流域径流输沙贡献率计算结果 Table 3 Calculation results of climate change and human activities' contribution to runoff and sediment load in the Dali River Basin

图6 1960—2015 年大理河流域年降水量-径流量和降水量-输沙量双累积曲线 Fig.6 Double accumulation curve of annual precipitation-runoff and precipitation-sediment load in the Dali River Basin from 1960 to 2015

3 讨论

3.1 淤地坝建设对径流输沙的影响

研究表明，黄河流域的年降水量并未发生显著增加[27]，根据1960—2015 年大理河流域年降雨的M-K 趋势检验结果表明，M-K 趋势检验统计量的绝对值均小于1.96，这意味着全流域年降水量均呈不显著的变化趋势（图7b）。对于黄土高原地区来说，人类活动变化中影响最为广泛的就是20 世纪50 年代开始在黄土高原地区实施的水土保持工程，该工程主要包括林草工程、梯田建设和淤地坝工程的修建[28-29]。其中，因为淤地坝具有拦沙淤地的直接经济效益，因而被黄土高原地区广泛推广使用，淤地坝工程的修建历时最长，修建规模最大[30]。图8 中所示为大理河流域1960—2011 年径流量和输沙量变化，其中实测输沙量为绥德水文站的观测值，实际输沙量为淤地坝逐年拦沙量和实测输沙量的加和。实测输沙量的变化基本与实际输沙的变化具有一致性。因此，实际输沙量与径流量的关系和实测输沙量与径流量的关系基本保持一致。根据李宗善等[31]的研究，黄土高原地区淤地坝已经超过10 万座以上，效益明显，直接发挥了拦截泥沙淤泥造地的功能，目前已经截留了280 亿t 水土流失总量，2002 年淤地坝农田规模达到3 200 km2，粮食产量是梯田的2～3 倍。在大理河“7·26”特大暴雨洪水事件中，建设有完备淤地坝系的韭园沟流域相比对照流域洪峰流量消减达到8 倍，洪水含沙量只有对照流域的三分之一。根据2011 年全国第一次水利普查，大理河流域共有骨干淤地坝279 座（图7a）。淤地坝的修建高峰期在20 世纪70 年代，同时2000 年后水利部实施淤地坝亮点工程，淤地坝的修建又出现了第二次高峰。淤地坝的修建直接拦截了大理河流域大量的泥沙，对流域径流产生了再调节和再分配的作用，径流的变化造成产沙输沙能力的减弱，因而间接减少了输沙量。

3.2 植被恢复对径流输沙变化的影响

自从1999 年中国政府在黄土高原地区实施了退耕还林政策，大规模的植树造林工程显著的增加了黄土高原的植被覆盖度[32-33]。特别是在大理河流域，NDVI 从1999—2015 年明显增加（图9）。根据M-K 检验分析，1999—2015 年大理河流域NDVI 均值呈现显著增加趋势，与径流和输沙的变化趋势相反。根据ULSE 土壤侵蚀的模型的原理，随着植被的增加土壤侵蚀程度可以降低，植被在一定程度上阻止了泥沙的产生，减少了输沙量[34]。根据梁越等[35]的研究，退耕还林后黄河河龙区间土壤侵蚀强度减弱，退耕还林工程对河龙区间减少作用从大至小呈现：中部-南部-北部。同时，研究表明由于近60年河龙区间降雨和降雨侵蚀力并未发生明显变化趋势，退耕还林后植被增加可能是小流域泥沙减少的主要推动力。