用于振动采收的有果有叶果树振动模型构建

许林云，刘冠华，周 杰，周宏平，蒋雪松，宣 言

（南京林业大学机械电子工程学院，南京 210037）

0 引 言

现有林果采收的主要方式为通过林果采收设备对果树主干或侧枝处施加振动激励，振动经过树枝传递到果实并引起果实振动响应，当果实的惯性力大于果实的果柄结合力时果实脱落[1]。研究果树的振动采收机理有助于开发林果振动采收装备。在针对果树的动态响应研究中，最常见的研究方法为动力学建模[2-5]和试验研究分析[6-10]。果树动力学建模方面，Miller[11]将树体简化为集中质量-连杆模型，并将杜芬方程与树木振动模型结合起来，对树木的非线性响应进行分析。Kenneth 等[12]通过多自由度的质量-弹簧-阻尼系统构建果树振动模型，将一级侧枝模型与主干模型相连接，二级侧枝模型与对应的一级侧枝模型相连接，研究了多级树枝振动。Murphy 等[13]构建了多级连杆模型，将多连杆模型果树振动方程在振动平衡位置附近简化为线性方程，求解出了多连杆果树振动模型的固有频率和振型，并利用模态分析方法计算了果树的响应。王琳[14]根据云杉的生态特性将其简化为一端固定、一端自由的变截面弹性杆模型，将树干的部分质量与树冠质量看作一个集中质量球固定在杆的顶端，求得了云杉的自由振动响应形式。翁凌云等[15]把Y 型果树简化为变截面楔形梁，将梁顶端施加一个分段树干质量与树冠质量的等效质量块，求得了其受迫振动下的响应。

近年来许多学者利用三维建模与有限元法对果树进行模态和振动响应分析[16-19]。Bentaher 等[20]通过对树木的树形结构测量，利用COSMOSM-(Geostar)数值模拟软件对果树进行了三维重构，并求解了果树在不平衡偏心块式激振下的响应情况。Peng 等[21]用三维软件构建了冬枣果树的三维模型，实测了冬枣树的密度、弹性模量和剪切模量，利用ANSYS 软件对冬枣果树模型进行了模态分析和谐响应分析。Burt 等[22]通过QSM 点云处理软件对威萨姆森林的点云进行处理，利用Abaqus软件构建树木风振有限元模型，通过数值模拟得到了在风振时树木的应力分布。贺磊盈[23]采用2 张不同角度的核桃树图像对核桃树进行了三维重建，并对重建的三维模型模拟果树侧枝修剪，用有限元软件对不同程度修剪的果树进行模态计算，结果发现随着侧枝树木数量的增加，固有频率出现下降趋势。王冬等[24]通过Pro/E 软件建立了3 种常见形态的果树有限元模型，计算了3 种不同激励下的果树响应，确定了3 种树型最合适的激振采收方式。

综上所述，传统的建模方式只适合将复杂多形态的果树极大简化后建模，有限元建模方法虽可构建与复杂形态果树的模型，但现有的建模方法均忽略了树叶和果实对果树的影响，而理论模型应对与实际复杂形态果树较一致的有果有叶果树建模才有实际应用价值及指导意义。本研究提出了将激光点云信息与有限元相结合，提取果树的骨架点及节点树枝半径，构建果树空间有限元模型。基于同种果树在其收获期间果实与树叶的分布规律基本一致的假设，通过对果实和树叶在果树上的分布进行统计分析，确定果实和树叶在果树上的分布规律，继而对模型节点上附加果实质量和树叶质量构建有果有叶的果树空间振动理论模型，并用银杏树对模型进行试验验证及分析。

1 果树空间有限元振动模型

1.1 有果有叶果树振动模型构建方法

将树枝看作空间圆柱梁，采用空间6 自由度圆柱梁进行三维建模。假设果树在小变形振动下为线性振动，可将果树的振动视为空间刚体振动，并将机械振动理论中的三维空间圆柱梁结构有阻尼一般振动微分方程应用于果树，形成果树振动微分方程如式（1）所示

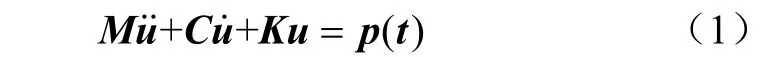
式中K、C 和M 分别为果树的刚度矩阵、阻尼矩阵和质量矩阵，其中质量矩阵M 由树枝质量矩阵Mz、树叶质量矩阵My和果实质量矩阵Mg三部分构成，果树刚度矩阵K 由树枝刚度构成；、和u 分别为节点加速度向量、速度向量和位移向量；p(t)为激励力向量。

依据有限元理论[25]可知6 自由度空间圆柱梁单元的质量矩阵和刚度矩阵分别如对称矩阵（2）和对称矩阵（3）所示

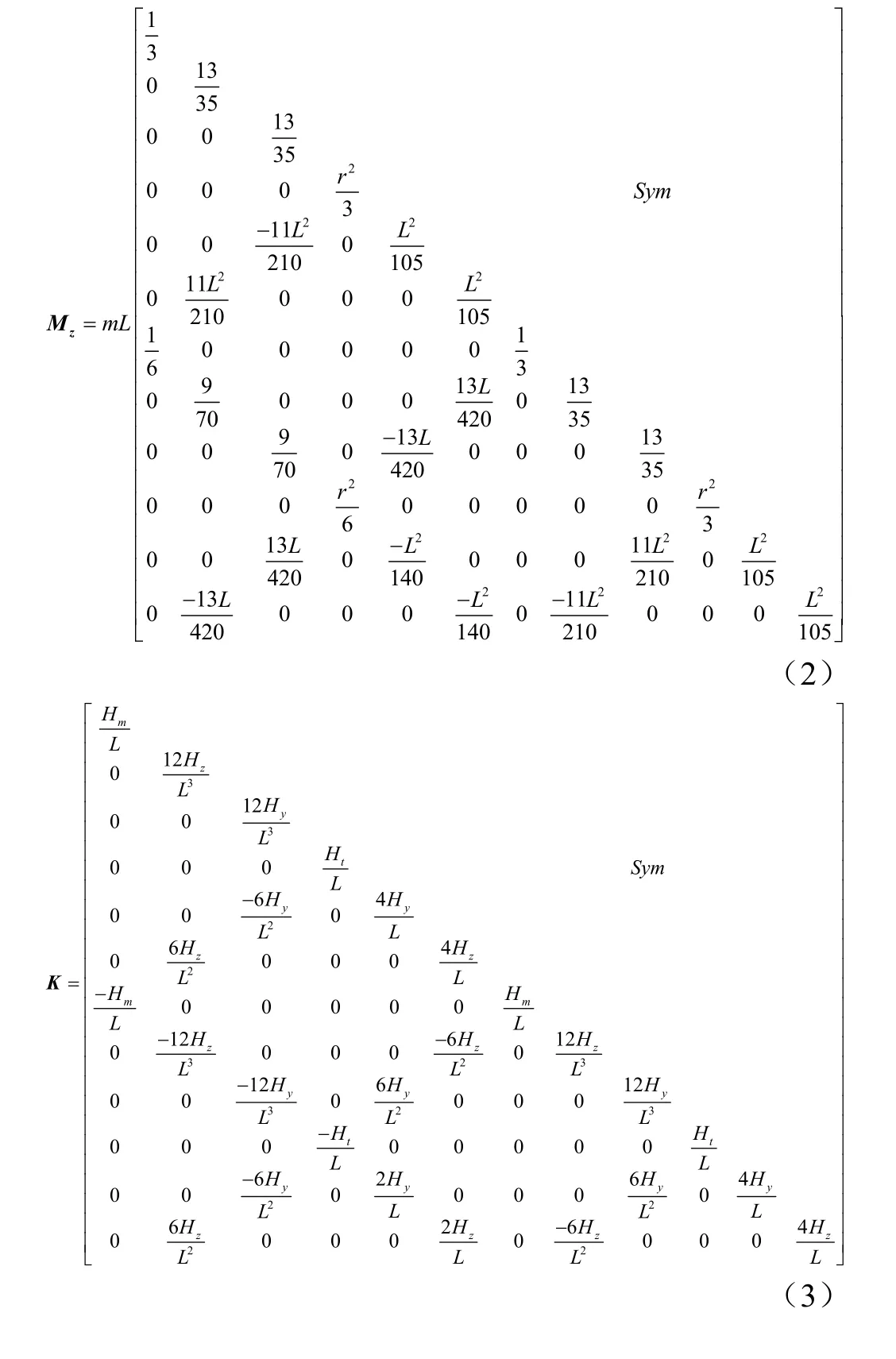
式中r 为对应节点圆柱梁的半径，mm，其所对应单元的截面积为A=πr2，mm2；m 为对应单元的单元质量，kg； L 是单元长度，mm；梁的拉伸刚度Hm=EA，N，其中E为果树的弹性模量，MPa；梁的扭转刚度为Ht=Gmr2/2，N·m2，其中G 为果树的剪切模量，MPa；绕Y 轴的抗弯刚度 Hy=Em(3r2+L2)/12，N·m2；绕 Z 轴的抗弯刚度Hz=Em(3r2+L2)/12，N·m2；Sym 表示省略部分关于对角线对称。

通过果树激光点云提取果树的骨架节点构建的果树振动模型，较人工测量手绘模型可以更好地重现果树的枝杆姿态。以激光扫描提取的骨架点为基础，将2个具有相邻拓扑关系的骨架点作为空间梁单元的2 个节点构成一个空间梁单元，树枝振动模型由已构建的单个单元按照拓扑关系依次连接而成，连接关系如图1所示。

图1 果树骨架模型示意图 Fig.1 Schematic diagram of fruit tree skeleton model

实际的果实采收期间，果树枝杆上有大量的树叶和果实，树叶和果实的质量会影响果树整体的质量分布，只使用果树枝干模型计算得到的模态参数与有果有叶的果树模型计算的结果存在很大差异。本研究提出根据果树的果实和树叶分布规律构建果树有果有叶振动模型。现有的研究中，已经有部分学者采用统计的方式对植物的生态特性进行了研究[26-27]。本研究设单位长度的树枝上果实和树叶的平均数量分别为ng和ny。单个果实的平均质量为mg，kg；单个树叶的平均质量为my，kg。则附加果实与树叶质量矩阵Mg和My如式（4）和式（5）所示

附加树叶与果实质量后的总质量矩阵如式（6）所示

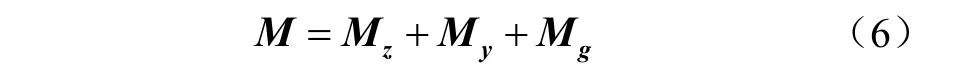
式（1）中的阻尼矩阵表达了树对运动能量的耗散，树木的阻尼是由树木振动过程中树木内部和外部摩擦共同作用的结果。Milne[28]对云杉的阻尼进行了分析，其发现树冠与邻近树木的碰撞占总阻尼的50%，其次为叶子运动时对应的空气阻尼占总阻尼的40%，树体自身的黏塑性阻尼占总阻尼的10%。Sellier 等[29]在研究树木风振时采用瑞利阻尼构建果树有阻尼振动模型。Moore[30]认为树体阻尼与枝条和树叶在树枝上的分布有关，且枝条和树叶实际上影响了果树树枝的质量分布，因此采用瑞利阻尼进行计算是合理的。综上所述，本研究采用瑞利阻尼构建果树振动模型。瑞利阻尼C 一般式如式（7）所示

式中α 为质量阻尼系数，β 为刚度阻尼系数。果树的瑞利阻尼系数可通过实测获取果树的多阶固有频率及对应的黏性阻尼系数，采用最小二乘法进行拟合，即可由式（8）确定α、β。

式中ωi为第i 阶固有圆频率，rad/s；ξi为第i 阶固有圆频率对应的黏性阻尼系数。

则第i 阶固有频率如式（9）所示

式中fi表示第i 阶固有频率，Hz。

1.2 计算有果有叶果树固有频率

由机械振动原理可知，系统有阻尼固有频率ωd和无阻尼固有频率ωn的关系如式（10）所示

式中ωd为有阻尼固有圆频率，rad/s；ωn为无阻尼固有频率，rad/s；ξ 为黏性阻尼系数。

许多学者的试验研究表明树木的阻尼比大约在0.2左右[28,31]在低频区有阻尼固有频率与无阻尼固有频率十分接近。由于果树实际阻尼很小，在计算果树固有频率时，可以忽略果树的阻尼项，在不施加外部激励时，则式（1）可简化为果树无阻尼自由振动微分方程如式（11）所示

根据线性振动理论中的模态振型定义，当果树处于某一模态振型ϕ 时，果树各点的振幅之比是唯一的。设果树在某一模态振型下振动时各点的位移振动响应如式（12）所示

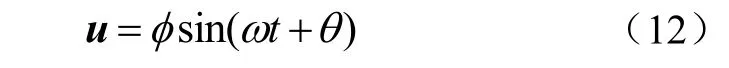
式中ω 表示响应频率，rad/s；θ 表示响应与激励之间的相位差，rad；t 表示响应时间，s。

将式（12）带入式（11）中约去共同因子后得到式（13）

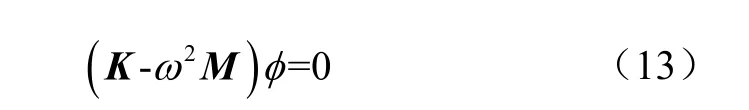
求解式（13）需给定边界条件，果树的边界条件主要为根部对果树的约束。Láng[32]在进行果树有限元分析时对树木的根部简化为弹簧-阻尼系统。Dupuy 等[33]构建了包括树根在内的有限元模型，要构建此类模型需要根部的几何形状，要将树根挖掘出来并进行测量，这样获取根部的形状是很困难的。Sillier 等[29]将根部简化为2 个扭转弹簧，保证果树能够绕水平面的2 个坐标轴转动。Wood 等[34]认为根部虽不能使树木非常牢固地固定在地面上，但这些学者认为这种现象对树木的固有频率影响不大。综上所述，构建树根的约束需在根部节点施加对应的约束条件，本研究考虑了Wood 等[34]的结论与实际计算的便捷性后，将根部约束简化为固定端约束。消去果树底部节点的6 个自由度后求解式（13）的特征行列式即可得到6 自由度三维空间梁单元构建的果树模型的固有频率。

2 银杏树三维模型构建

为验证上节所构建的果树振动模型的准确性，本研究以银杏树为研究对象，在南京林业大学校园内采伐一棵有果有叶的适用于室内试验的小型银杏树（图2a）进行模型构建及相关试验测试，采伐时间为2019 年9 月，正值果实成熟时期。采伐后的果树用地钳将果树根部固定在地面上。为研究有果有叶、无果有叶和无果无叶不同状态果树的频谱特性，采用人工干预的方式，先从有果有叶状态时的果树进行测试，然后人为摘去果实形成无果有叶果树，最后摘去树叶形成无果无叶果树（图2b）进行各项试验测试，所有室内试验在果树采伐后的3 d 内完成。

要精准确定果树骨架点，构建果树骨架振动模型，只能先对无果无叶银杏树通过激光扫描获取骨架点云，然后再在骨架振动模型基础上，通过分别添加果实与树叶分布阵，获得有果有叶的果树振动模型。

2.1 银杏树树枝点云处理及模型构建

本研究采用二维激光雷达扫描图2b 所示的果树，获取果树骨架点云数据，点云采集系统（图3a）包括二维激 光 传 感 器（ UTM-30LX ） 、 2.5 m 丝 杠 滑 台（FLS40L100010C7）、步进电机及驱动器、STC51 单片机、24 V 直流电源和PC 电脑。通过单片机控制滑台以3 mm/s 带动激光扫描仪，将丝杠导轨放置在距果树中心5 m 的圆周上，以120°夹角分3 次对果树进行扫描，可全面获取果树枝杆的形态信息。此外，在距果树中心1 m范围内还需将3 个直径不同的靶标球布置在3 个不同高度的位置上，且要求放置各靶标球时对扫描不会产生遮挡果树或相互遮挡问题。

图2 固定于室内地钳上的银杏树 Fig.2 Ginkgo tree fixed on indoor ground clamp

图3 点云扫描装置及扫描方法 Fig.3 Point cloud scanning device and scanning method

3 个位置点3 次扫描果树树枝点云图可通过3 个靶标球进行拼接，拼接后的原始点云通过半径法对果树原始点云进行去噪处理，对去噪后的点云采用基于点云主方向移动圆柱体的方法获取果树的骨架点，由于受拼接精度和激光扫描精度的影响，通过点云提取的果树骨架点截面半径会存在某些粗大误差，对误差较大的数据采用人工测量实际果树的方式进行修正，最终构建果树空间梁单元振动模型（图4）。

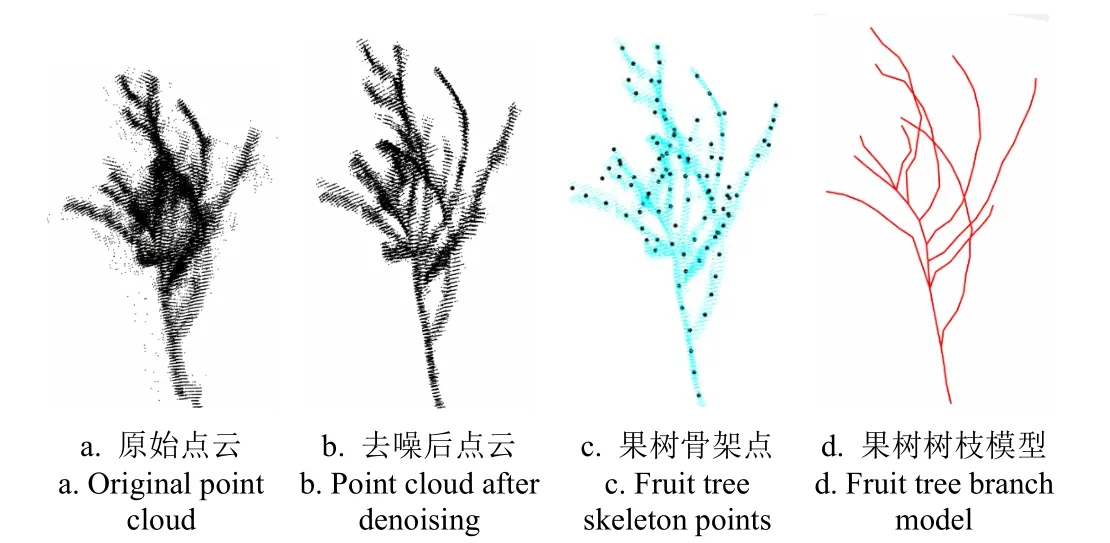
图4 果树建模过程 Fig.4 Fruit tree modeling process

2.2 银杏树果实分布特性

银杏树的果实和树叶只会生长在腋芽处，本研究对室内试验银杏树上的树叶和果实进行统计分析，树叶、果实及腋芽分布状态如图5 所示。

图5 树叶、果实及腋芽局部分布图 Fig.5 Distribution of leaves, fruits and axillary buds

果树上共计335 个腋芽，其中长果实的腋芽共有242个，约占腋芽总数的72.2%。由于构建有果的果树模型需要获得单位长度树枝上的果实的平均质量与平均数量，因此统计内容包括相邻长果的腋芽分布间距、同一长果腋芽处果实生长的数量和同一腋芽上果实的平均质量。并对统计出的各参量分布规律用正态分布进行拟合，拟合公式如式（14）所示

式中a 和b 为拟合常系数，u 为分布期望值即均值，σ 为分布标准差。对应各参数分布如图6 所示。

生长果实的腋芽间距分布如图6a 所示，生长果实的腋芽间距主要集中在3～6 cm 之间，占比为81.4%，整体的分布规律为均值4.24 cm，标准差1.93 cm 的正态分布。由图6b 可知，腋芽处生长的果实数量主要集中在4～10个之间，其中生长有4、6 和8 个果实的腋芽数量明显高于其他果实个数的腋芽数量，其原因是绝大多数银杏果在一个果柄上会并列生长出2 个果实，所以果实数量出现双数的概率明显大于奇数，因此总体分布规律拟合曲线相决定系数较低，只有0.757，单个腋芽处生长果实数量的分布为均值5.69 个，标准差为4.84 个的正态分布。由图6c 可知，生长果实的腋芽主要集中在直径为3～10 mm 的树枝上，占比为93.0%，总体分布规律为均值为6.09 mm，标准差4.09 mm 的正态分布。由图6d 可以发现腋芽处的果实质量主要集中在5.9～6.5 g 之间，占比为81.4%，其分布为均值6.15 g，标准差0.45 g 的正态分布。除了腋芽处生长的果实数量拟合正态曲线的相关系数较低，其余3 种情况拟合正态曲线时的决定系数均高达0.922 以上，说明各分布规律均较好地符合正态分布。

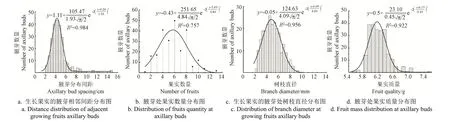
图6 果实分布规律 Fig.6 Fruits distribution law

2.3 树叶分布特性

对试验银杏树上的树叶分布进行研究，共计317 个腋芽处生长树叶，约占腋芽总数的94.6%。对生长树叶腋芽的腋芽相邻间距、同一腋芽处生长树叶的数量、同一腋芽处生长树叶的平均重量和生长树叶腋芽处的树枝直径进行统计，各参数分布如图7 所示。

图7 树叶分布规律 Fig.7 Leaves distribution law

由图7a 可知，生长树叶的腋芽间距主要分布在2～6 cm 之间，占比为86.1%，腋芽间距分布规律为均值4.04 cm，标准差2.26 cm 的正态分布。由图7b 可知，腋芽处的树叶数量主要集中在3～7 片之间，数量分布最多的为5 片，树叶数量分布符合均值为4.85，标准差为2.84的正态分布。由图7c 可以看出，能够生长出树叶的腋芽主要分布在直径2～10 mm 的树枝上，占比为85.8%，有极少数的直径为2 mm 以下、10 mm 以上的树枝也存在少量的树叶，其分布总体符合均值4.95 mm，标准差4.18 mm的正态分布。根据图7d 所示，叶片的平均质量主要分布在0.3～0.6 g，占比为84.9%，其分布符合均值0.40 g，标准差0.28 g 的正态分布。总体来说，腋芽处树枝直径按正态分布曲线进行拟合时的决定系数最低，但也达到0.852，其他3 种参数拟合时的决定系数均高达0.969 以上，说明具有较好的正态分布规律。

2.4 有果有叶模型

为验证上述果实与树叶分布规律的准确性。本研究将上述对果实、树叶所获得的各分布规律，与在南京林业大学校园内生长的10 a 以上的5 棵大型银杏树上随机选取的共计150 个腋芽处的树叶与果实分布规律进行对比，各项分布中误差最大为树叶分布中的腋芽处树枝直径，相对误差为7.6%，其主要原因可能为室外果树具有较多生长有树叶的末端细枝，导致室外果树分布均值偏小。其余各分布的均值相对误差均<5%，对比结果均满足以上的各自正态分布规律，说明采用这些分布规律对果树进行构建有果有叶的动力学模型是可行的。

应用上述获取的银杏树果实和树叶的分布规律，对银杏树枝杆模型按以下规律添加果实质量：生长果实的腋芽间距为4.2 cm，并结合实际果实生长双数居多的现象，单个腋芽生长果实数量为6 个，单个腋芽上生长果实的平均质量为6 g，则对应1 cm 长度的树枝上果实数量密度ng=1.43 个，应用在果实质量矩阵中的单个果实平均质量mg=6×10-3kg。依据生长果实的腋芽处树枝直径分布可知，实际果实大多生长在直径3～10 mm 的树枝上，因此不能对果树整体枝干上进行附加果实质量，而只能在直径符合特定条件的枝干上附加果实质量。因此只在银杏树树枝模型中直径≤10 mm 的单元，应用式（4）计算附加果实质量矩阵Mg。

基于树叶的分布规律，在银杏树枝杆模型上按以下规律添加树叶质量：生长树叶的腋芽间距为4 cm，单个腋芽生长叶片数量为5 个，单个腋芽上生长树叶的平均质量为0.4 g。则按1 cm 长度树枝上树叶密度ny=1.32 个，应用在树叶质量矩阵中的单个树叶平均质量my=4×10-4kg，且只对枝杆模型中直径≤12 mm 的单元，应用式（5）计算附加树叶质量矩阵My。

通过果实和树叶的分布特征可以看出，银杏的树叶质量明显小于果实的质量，对银杏树进行建模时，可进一步简化即忽略银杏树的树叶质量。但本研究为全面体现有果有叶的建模方法，并不忽略树叶的质量，依然根据有果有叶的质量矩阵进行计算。对其他树种来说，特别是果实与树叶质量均对果树质量分布有明显影响的树种，在进行果实建模时同时附加果实和树叶质量矩阵是十分有必要的。

应用式（6）即可计算得到银杏树有果有叶振动模型的质量矩阵，结合式（13）即可计算银杏树有果有叶模型的固有频率。

3 银杏树的频谱特性试验与仿真分析

银杏树频谱特性测试方法采用冲击力锤法，具体测试方法为在果树主干上布置一个加速度传感器测点（测点0），在6 个主要侧枝上布置6 个加速度传感器测点（测点1～6）。为减小传感器质量对测试结果的影响，本研究选取的侧枝测点位置均尽可能距离主干较近即具有较好的刚性，同时又能测试出反映该侧枝的频谱特性，具体布点如图2 所示。通过在测点0 处施加冲击信号，测得0～6 测点的加速度响应信号，即可由式（15）计算果树各个测点的的传递函数。

式中H(f)为果树的传递函数；Y(f)为加速度信号的傅里叶变换；F(f)为力锤冲击信号的傅里叶变换。

频谱测试装置包括冲击力锤（LC-02A）、三向压电式加速度传感器（CA-YD-141）、电荷放大器（YE5853A）、数据采集系统（NI cDAQ-9174）和测试分析软件（CRAS V7.1）。振动采收应用最多的为偏心块式激振方式，偏心块式激振的工作频率区间主要为15～25 Hz[35]，因此本研究对果树频谱特性的频率关注范围设定在0～30 Hz。

3.1 银杏树的频谱特性试验分析

通过测试及数据处理可获取各测点传递函数对应的频谱曲线，如图8 所示为有果有叶频谱曲线，由于果树存在较多固有频率，图中仅标识较为明显波峰对应的频率即各固有频率。各测点频谱曲线中的基频均为0.39 Hz，在0～5 Hz 内存在大量的低矮密集波峰，即果树在低频阶段聚集大量的固有频率，这与De Langre[36]的研究结果是一致的，即在低频区出现大量峰点是由于植物的材料柔性大，导致存在多数固有频率集中在10 Hz 以下。在5 Hz 以下的各峰点单位力引起的加速度幅值基本处于1 mm/(s2·N)左右且峰宽较窄；高于5 Hz后频谱曲线的波峰开始变得稀疏、峰宽变宽，即在有果有叶的情况下果树的高频振动加速度幅值变大且对应阻尼也增大。

图8 三种状态下的果树频谱曲线 Fig.8 Spectrum of fruit tree in three states

去掉果实后，各测点频谱曲线较去除果实前有了一定变化。果树在无果有叶状态下的基频为 0.46 Hz，比有果实时的基频略大，且在0～3 Hz 内密集波峰基本消失，而在5～10 Hz 内由原平缓上升状态变为出现多峰点。各测点频谱曲线在10～30 Hz 的波峰突出较为明显，但单位冲击力引起的加速度幅值并无明显变化趋势。

在无果无叶状态下，果树的基频明显增大为2.03 Hz。在低频0～5 Hz 内波峰较少，但在5～10 Hz 内出现了较多小型波峰，在10～30 Hz 出现大量明显的较高波峰。与有果有叶和无果有叶状态下相比较，无果无叶状态下的各测点频响函数的单位力激发的加速度幅值显著增加，这主要是由于去除树叶后，果树的阻尼系数明显下降。

综上所述，随着逐渐去除掉果树的果实和树叶，果树的低频固有频率集中出现的区域由0～5 Hz 向5～10 Hz 区域逐步变化，这是由于随着果实和树叶的去除，果树的整体质量在下降，但树枝的整体刚度基本没有变化。从固有频率的基本定义可知，其值会随着刚度与质量比的增大逐渐增大，这与上述测试结果相一致。此外，各测点频谱曲线幅值在去掉果实和树叶后有了明显的提升，尤其在去掉树叶后增加特别明显，说明树叶是影响果树振动幅值的主要因素，即树叶的阻尼效应明显大于果树果实和自身材料的阻尼效应。说明树叶和果实的质量分布对果树的频谱特性分布有明显影响，在研究林果采收时不能忽略果实与树叶附加质量的影响，因此构建有果有叶的振动模型才能有效反映实际果树。

3.2 仿真结果分析

基于第2 节构建的银杏树有果有叶有限元模型，利用MATLAB2017 计算该模型的固有频率。为确定计算模型的所需果树的密度、弹性模量和剪切模量参数，本研究通过在校园内其他银杏树上进行随机取样，将样本木材加工成27 个300 mm×20 mm×20 mm 的木条样本，测量木条质量并计算得银杏树的密度为1 250 kg/m3。使用电子万能试验机（CMT6104）测试材料的弹性模量，取27 个样本的平均弹性模量4 713.9 MPa 作为有限元分析模型的弹性模量，取泊松比为0.3，计算可知剪切模量为1 813.0 MPa。由于仿真计算结果和试验测试结果所得固有频率较多，为方便比较试验结果与仿真结果，通过2个频率区域进行验证模型的准确性：1）将低频区域前15阶固有频率的计算值与实测值进行比对，是为验证基频及低阶频率区域所构建模型的仿真计算准确性；2）在中高频15～25 Hz 区域内将两者进行比对，主要是验证在常用振动采收频率范围15～25 Hz 内的仿真模型的计算准确性。

针对果树有限元模型计算所得的固有频率出现成对现象，即连续出现相邻2 个固有频率值十分接近，这是由于仿真模型采用圆柱梁单元，而对称的圆柱梁会在同一固有频率或称模态频率下沿轴向截面2 个正交方向上产生2 个相互垂直的弯曲振型，但由于实际树枝上存在着各种小侧枝且树枝本身很难轴向对称分布，从而会出现一对对的非常接近的固有频率值。因此，本研究将成对出现的固有频率以较高值作为同一阶固有频率。一般仿真计算的固有频率要多于实测的固有频率，将实测频率与仿真计算频率比对，与仿真计算频率接近的实测频率作为同一阶频率。仿真果树模型密度与实际密度存在的差异会导致质量矩阵的误差，枝杆模型的弹性模量与剪切模量与实际的差异会导致刚度矩阵的误差，因此实际计算出的固有频率存在一定误差，Siller 等[29]采用修改模型的弹性模型与等效刚度使基频误差从20%相对误差下降到1%以内，本研究采用类似方法将实际树木密度和弹性模量分别提升了15%和降低了10%，3 种模型的原基频计算精度及调整后的计算精度如表1 所示。仿真模型经过调整后，无果无叶状态下从最大的相对误差14.8%，明显降低为0.5%，且其余2 种状态下的仿真基频与实测基频完全吻合，即相对误差为0。

表1 仿真基频与调整仿真基频表 Table 1 Simulated fundamental frequency and adjusted simulated fundamental frequency

将调整后的前15 阶固有频率的仿真与实测结果列入表2 中，将15～25 Hz 范围内固有频率的仿真与实测结果列于表3 中。实测中的主要固有频率已在图8 中表示出来。

由表2 可知，无果无叶果树模型仿真前15 阶固有频率主要集中在10 Hz 以下，基本呈现均布分隔状态；与实测结果相比对，实测中未出现第2、5、6 阶频率，其余12 阶仿真值与实测值非常接近；仿真计算最大相对误差为6.67%，平均相对误差为2.03%，且其中4.69、5.54、7.81 Hz 在实测频谱曲线中几乎为各个测点均出现的共同固有频率点。4.69、5.54 和7.81 Hz 振型图如图9 所示。可以看出这3 个振型图中大部分侧枝均有较明显的振幅，但不同频率下各枝的振型与振动幅值不同。无果有叶状态下，各阶仿真频率与无果无叶模型相比出现明显下降，致使各阶频率间隔明显缩小，即前15 阶固有频率集中在3 Hz 以下；仿真前15 阶固有频率中只有9 阶固有频率在实测中出现，仿真计算最大误差只有3.85%。有果有叶状态下，前15 阶仿真固有频率进一步降低，密集处于1.12 Hz 以下，绝大多数仿真频率在实测频谱曲线中未能出现，只出现了5 阶固有频率，因较低频率区内激振力引起的加速度响应灵敏度较低，有些固有频率较难激发起来，即在频谱曲线中难以体现出来，能在实测中体现出来的各阶固有频率最大相对误差为2.75%，平均相对误差为1.36%。

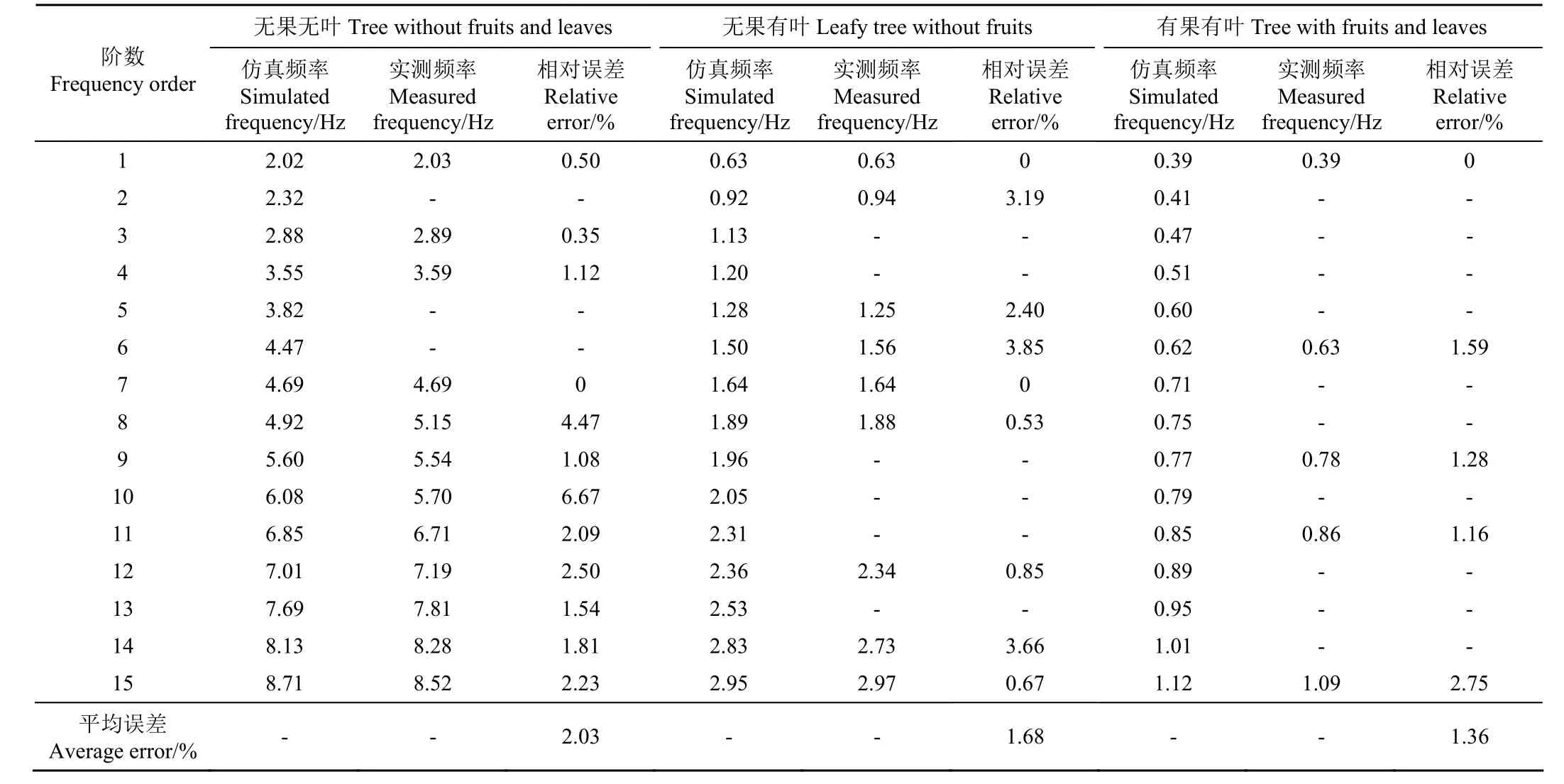
表2 前15 阶仿真与实测固有频率 Table 2 Top 15 steps of simulated and measured natural frequency

图9 部分振型图 Fig.9 Partial mode shape diagram

表3 15～25 Hz 仿真与实测固有频率 Table 3 15-25 Hz simulated and measured natural frequency

由表3 可知，在15～25 Hz 频率区间内，无果无叶状态下共有7 阶仿真固有频率，实测频率对应出现了5 阶；无果有叶与有果有叶状态下，均有10 阶仿真频率，实测频率分别对应出现了7 阶与6 阶，均比前15 阶频率中对应程度高得多。3 种仿真模型的最大相对误差分别为5.76%、2.06%和1.98%，平均相对误差分别为2.32%、0.82%和0.95%。

综上所述，仿真固有频率多于实测频谱曲线体现出来的固有频率，这是因为实测的频谱曲线上某些部位的曲线波峰非常微弱，只使曲线出现微弱起伏，难以判断此处是否存在固有频率，即并未将其标注出来，致使实测固有频率数会少于仿真频率数。因此，在处理仿真频率与实测频率对应关系时，是将实测固有频率与仿真频率中非常接近的固有频率值作为对应的同等阶次。无果无叶果树的各阶固有频率分布较稀疏，而随着树叶与果实的添加，各阶固有频率明显越来越密集，并在实测中所能体现出来的对应固有频率越来越少。同时仿真计算的固有频率只要在实测中能体现出来，其相对误差均较低，最大不超过6.67%，说明所构建的有果有叶模型是可行的，具有一定的实用价值。

3.3 计算误差分析

从试验结果中可以看出，对果树附加质量后的计算精度相较无果无叶模型的计算精度提高，可应用以下相关计算公式进行分析论述。为方便理解，只取其中某一树枝单元基于集中质量方程进行论述，假设构建模型时给定该单元树枝的质量和刚度分别为mz和kz，而实际质量和刚度分别为mz+Δmz和kz+Δkz，其中Δmz和Δkz分别为树枝的质量误差和刚度误差且Δmz和Δkz分别远小于mz和kz，假设实际树枝的无误差精确振动方程如式（16）所示

式中mz为树枝质量，kg；kz为树枝刚度，N/m；Δmz为树枝的质量误差，kg；Δkz为树枝的刚度误差，N/m；Δmz和Δkz分别远小于mz和kz；x 表示位移，m；x˙˙表示加速度，m/s2。

则建模型计算获得的固有频率误差Δf 如式（17）所示

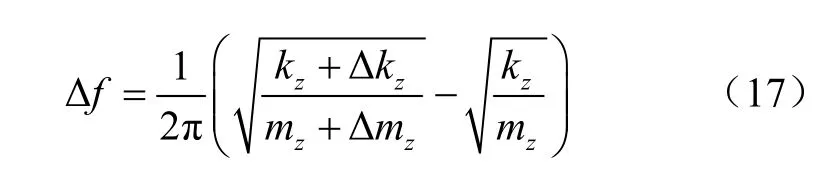
式中Δf 为固有频率误差，Hz。

树体上附加果实和树叶质量后并不会对其刚度产生影响，因此式（17）中仅考虑质量误差Δm。对式（17）进行简化处理并略去高阶无穷小项后得式（18）

附加树叶和果实质量后的计算误差分别如式（19）和式（20）所示

式中Δƒz+y为无果有叶固有频率计算误差，Hz；Δƒz+y+g为有果有叶固有频率计算误差，Hz；my为树叶质量，kg；mg为果实质量，kg；Δmy为树叶质量误差，kg；Δmg为果实质量误差；且Δmy和Δmg分别且分别远小于my和mg。

假设树叶质量和果实质量的相对误差与树枝质量相对误差处于同一数量级，则由式（18）～式（20）可知，附加质量后的分母上的项 mz+my+mg与分子上的项Δmz+Δmy+Δmg的幂次数分别为1.5 和1，误差中的分母项的增加值远大于分子项的增加值，因此固有频率计算误差随着附加树叶质量和果实质量减小。综上所述，果树模型在刚度不变的情况下，随着附加较准确的树叶质量与果实质量，可以减小单纯树枝建模不准确所带来的计算误差。

4 结 论

本研究基于对无果无叶果树激光扫描进行三维重建，建立有果有叶果树的仿真计算模型，并通过试验对模型进行验证。具体结论为：

1）将激光点云与有限元分析相结合，通过提取果树枝杆骨架点和树枝半径，将树枝看作空间圆柱梁，通过分别构建果树的质量矩阵、刚度矩阵与阻尼矩阵，结合果树果实和树叶的质量矩阵，构建有果有叶果树空间6自由度圆柱梁振动模型。

2）提出了构建树叶、果实与腋芽沿果枝生长方向的正态分布形态，找到了银杏树果实和/或树叶的腋芽数量与腋芽间距、果实或树叶数量、树枝直径、果实或树叶平均质量的分布规律，确定了银杏树空间振动模型中果实与树叶的分布质量及质量矩阵。且果实与树叶质量分布矩阵的构建方法可应用于其他品种果树有果有叶振动模型的构建。

3）对银杏树有果有叶、无果有叶和无果无叶3 种状态进行频谱特性测试，发现树叶和果实的质量会明显影响果树的固有频率数量及其分布。说明只构建果树的枝干模型确定果树的频谱特性，无法应用于果树实际果实基于频谱的共振采收。

4）通过对银杏树具体的仿真建模和试验获得的各阶固有频率进行比对验证，仿真计算固有频率数量要多于实测所体现出来的固有频率数量，但实测固有频率均可在仿真频率中找到十分相近的值，且仿真模型的果树各枝振型幅值与实测频谱曲线中各枝的加速度响应幅值之间的对应关系基本吻合。有果有叶仿真模型在常用采收频率15～25 Hz 内最大相对误差均<6.67%，并对仿真模型的计算误差进行了分析说明，证明本研究所述果树建模方法的可行性。

本研究所构建的果树振动模型，可通过激光扫描设备应用于田间果树固有频率的快速计算，从而可确定田间采收设备的实际采收频率，此为本研究的后续进展。