课堂教学的有效性

韩琼 方学士

【摘 要】 《数学课程标准》的基本理念是义务教育阶段的数学课程应突出体现基础性、普及性和发展性，使数学教育面向全体学生，实现人人学有价值的数学、人人都能获得必需的数学和不同的人在数学上得到不同的发展。同时指出，数学是人们生活、劳动和学习必不可少的工具，是人类的一种文化。如何让更多甚至全部的学生在课堂上学到知识，重要的就是激发学生的兴趣，这样可以大大提升课堂有效性。

【关键词】 课堂教学;课堂有效性

一、问题提出

《数学课程标准》的基本理念是义务教育阶段的数学课程应突出体现基础性、普及性和发展性，使数学教育面向全体学生，实现人人学有价值的数学、人人都能获得必需的数学和不同的人在数学上得到不同的发展。由于每一个学生的认知水平与能力的不同，他们所接受的知识程度也不同，于是我们在教学中常安排层层递进的模式，从旧知识到新知识循序渐进，步步为赢;布置作业时常分必做题与选做题，可谓考虑周到，让每一个学生都能得到相应的提高。但事与愿违，学生之间的差距随年级的增大而增大。

如何让更多甚至全部的学生在课堂上学到知识，使课堂教学更有效，最重要的就是激发学生的兴趣。于是，教师常想出许多方法，其目的都是培养学生对数学的学习兴趣、有成就感。以下谈谈促进课堂教学有效性的方法与建议。

二、实践体會

1.利用问题串的魅力

利用问题串的教学方法，可以使教学内容精练、简洁，常利用一道简单的基本题进行一题多变、一题多解，有时也可以一法多用，产生有梯度、有层次的一系列问题，让学习有困难的学生感受到问题的本源，让学有余力的学生及时巩固与提升。例如：在初一学到“用字母表示数”时，常遇到找规律的题，这类题可以培养学生思维能力，但给教师教学带来一些困难，如何引导是关键。例如一道填空题：。

由于此题没有提示，是一道填空题，没有梯度的设置，学生不知道从何入手。于是在当时教学中作了以下尝试：

[导1]计算：与的值相等吗？（结论：相等）

在初一学生的认知能力下，无法摸索出“拆项法”，这时给予正确的“道路”，虽扼杀他们的创新，但可以为新的“创新”埋下伏笔，正所谓“借鸡下蛋”。

[导2]计算：与的值相等吗？（结论：相等）

[导3]计算：与的值相等吗？（结论：相等）

[导4]你能发现其中的规律，用一个字母n表示出你所发现的规律吗？这是一步从特殊到一般的转化，是学完“用字母表示数”后的一次应用。（结论：）

利用你得到的规律，进行计算。容易作如下处理：

利用规律进行拆项，结合首尾相消得到结论，并让学生感受结果的有趣性，即。课后，我不禁在想：我扼杀了学生的创造思维，因为给了他们过多的问题串作为铺垫，使一道经典的问题没有深度，而且没有拓展，只做了“对题论题”，于是，利用一次课余时间对此题进行了变式与拓展。

【变题1】求的值。

【变题2】求的值。

思路1体现了学生思维的连贯性和一定的分析能力;思路2体现了对知识的整体把握性和一定的思维能力，可以说是创造性思维的体现，是我当时没有备课到的。

而后我又进行了拓展，采用填空的形式进行考查。

【拓展1】观察规律填空：2，6，12，20，____，42，_____。

让学生去发现其中的规律，学生得到第2个数比第1个数大4，第3个数比第2个数大6，第4个数比第3个数大8，于是得到第5个数应比第4个数大10，填入30，以此类推，另一空填56。我接着问学生第9个数是多少？（学生很有兴趣在算出是90）那第90个数呢？此时学生没有办法，经过一句“想想问题的本源”，部分学生恍然大悟，得到第90个数为8190。原来这组数学的规律可以看成是：，这样联系了先前的知识，（其实还可以作1，3，6，10，15，21……类似规律填空的训练）并进行了拓展2的训练。

【拓展2】求的值。

此题可以说是原题的变式，也是拓展1的延伸或变式，学生没有出现一个一个计算，很快利用上述方法进行了求解，考查了小学的分解因式的知识。我进行了总结，并提出了一道新的问题。

【拓展3】通过上述问题，请你在1到100中找出10个自然数，使它们的倒数之和等于1。

通过变题与拓展，学生对这一拆项的问题基本掌握，于是，我又“趁热打铁”，进行了延伸，作为学有余力的学生的家庭作业。

【延伸1】对进行拆项，使它等于某两项的差。

这是一个开放问题，学生的答案都是正确的，因为只要两项之差等于即可。主要培养学生的开放性思维。

【延伸2】用一个等式建立起与的数量关系。

这是一个承上启下的问题，一方面让学生检验第一问的拆项的正确性，为下一步服务;另一方面考查学生对这类问题的理解与掌握程度。

【延伸3】求的值。

通过问题串，挖掘一道问题的深度，联系这一问题的问题链，建立问题的更大“问题链”，举一反三，让学生感受难题也是由基本的简单题变化得到的，从而激发学生学习的兴趣，提升课堂教学的有效性。

2.多用现实生活模型

记得有一次与朋友聊天时，他问了这样一个“玩笑”题：“统一”与“茅盾”有何关系？答案是：由于“统一”是方便面，“茅盾”是人，所以没有关系！

这是一道很有趣的问题，于是我在此基础上进行了“大胆”的“遐”想（瞎想）。可以说，这一问题是四大数学思想的较好的、通俗的教学素材。理由如下：

当“茅盾”爱吃方便面时，此时是爱与被爱的关系;当“茅盾”不爱吃方便面时，此时是不爱与不被爱的关系。于是，进入了数学的思维空间，从中我们得到分类讨论的思想方法。

当“茅盾”由于工作、学习原因，不可能天天如此，今天与明天也许不同，于是我们需要统计，列表，再利用数形结合进行思考，很容易发现名人的生活规律。

当“茅盾”爱吃方便面时，我们一定会关心“名人”的“八卦”，比如，他到底一天能吃多少，一年呢？一生呢？假设他一天吃x包，于是有了365x包，等等，从中得到函数和方程的思想方法。

当“茅盾”不爱吃方便面时，我们一定会去思考他为什么不爱吃？他到底爱吃什么？这便有了转化和化归的思想方法。

虽然这一“玩笑”缺乏数学的严谨性和科学性，但在教学中起到很好的启发效果，记得给初二学生教学时，学生不仅记住了“玩笑题”，更记住了“题外题”—四大数学思想。利用生活之事，不仅让学生明白生活中处处有数学，而且能很好地抓住学生的心灵，感觉当时学生对这一堂课的印象极深，回想他们那时的眼神，我一定要大胆让生活变得数学化，让数学生活化，培养学生学习的兴趣，这一有趣的教学收到了效果，对一些大胆的创新，我们何乐而不为呢！

其实，在生活中充满了数学，班费开支、手机话费、贷款（利息）、股票、土地問题、奥运等，例如某年的存款利率多次调整（总共10次），当年宁波市中考就考了一道有关存款利率的大题，每年出现民生问题，如话费、垃圾分类等等，我们应该抓住时代气息，关注实际生活，用现实数学模型鼓舞学生。

3.注重数学史的应用

数学史记载了民族的兴衰、研究的成败，引人数学史知识不仅是爱国主义教育，更是梳理数学内容、感受知识的发生过程，立体地、人文地、逻辑地展现数学的魅力，可以激励学生的兴趣。而数学史不仅仅可以发现数学本源或本质，更能让学生全面了解问题本质，更快记忆并掌握数学知识内容。

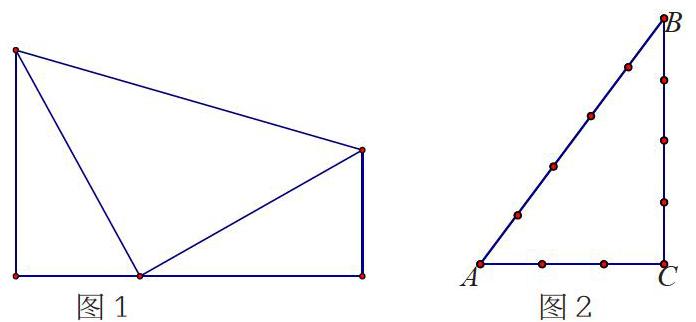
三次数学危机的感染，让学生明白数学发展的艰辛，在初一学到无理数，给出了第一次数学危机，教育珍爱生命的同时，感受数的第一次扩充的前前后后，潜意识地培养学生对数学的热爱，同时，对圆周率π与刘徽、祖冲之、卢道夫等人的故事，让学生背诵卢道夫墓碑上的把π的近似值算到小数点后35位数的一系列数学史，让学生感受无规律中的有趣性。进入初二，反证法证明是对无理数的一次补充，用一名数学家的灾难充分肯定了无理数的存在;再如，勾股定理的中西结合，多名字的定理，感受数学的发现犹如牛顿吃苹果，需要观察与思考，介绍美国第二十任总统伽菲尔德的故事：1876年一个周末的傍晚，散步的伽菲尔德发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。由于好奇心驱使，伽菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。伽菲尔德便问他们在干什么，那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边长分别为3和4，那么斜边长为多少呢？”伽菲尔德答道：“是5呀。”小男孩又问道：“如果两条直角边长分别为5和7，那么这个直角三角形的斜边长又是多少？”伽菲尔德不假思索地回答道：“那斜边的平方一定等于5的平方加上7的平方。”小男孩又说：“先生，你能说出其中的道理吗？”伽菲尔德一时语塞，无法解释了，心里很不是滋味。于是，伽菲尔德不再散步，立即回家，潜心研究小男孩给他出的难题。他经过反复思考与演算，终于弄清了其中的道理，并给出了简洁的证明方法（如图1所示）。

古埃及人用下面的方法得到直角：把一根长绳打上等距离的结（12段），然后用桩钉如图2那样钉成一个三角形，其中∠C便是直角。你能说出其中的原因吗？让学生感受勾股定理及其逆定理的作用。还有，欧拉公式、七巧板、哥德巴赫猜想等有趣的数学问题或数学史。当然，也包括中国古代数学的不足，用先进和“落后”的数学史激励学生正确看待“中国数学”的传统，产生正确的民族意识，感受数学是全人类的财富。正如陈省身先生说过：“21世纪数学大国，是要和世界上各国的数学家能够独立、平等地进行交流。”

三、总结反思

要使全体学生实现人人学有价值的数学、人人都能获得必需的数学和不同的人在数学上得到不同的发展的目标，让课堂教学充满创新活力，有效的同时，还要有趣、有用起来，教师是课堂的创造者与开放者，是学习活动的组织者、引导者和参与者。我们要抓住生活气息、时代气息和自身发展，让学生在课堂里有所发展，课堂教学有效性至关重要，只有保持课堂教学的有效性，学生才会少走“冤枉”路，得以发展。