格上基于KEM的认证密钥交换协议
2020-07-21赵宗渠黄鹂娟马少提
赵宗渠,黄鹂娟,范 涛,马少提
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
0 概述
认证密钥交换(Authenticated Key Exchange,AKE)协议可使通信方在有主动敌手的信道上建立安全的共享会话密钥,同时实现彼此身份的相互认证,在后续的对称密码中能够保证数据的完整性和真实性。目前多数AKE协议的安全性依赖于大整数分解和离散对数的Diffie-Hellman[1]困难问题,随着量子计算技术的发展,此类问题在多项式时间算法下是可解的,这将给现有协议带来安全威胁。格上构造的公钥密码体制因其运算简单、可并行性和抗量子攻击的优点,将在后量子时代成为最有效的解决方案之一,基于格的AKE协议因此成为学术界的研究热点。
基于格的AKE协议[2-4]可以抵抗量子攻击,解决经典困难问题下协议的安全性问题,但不能降低通信复杂度并实现认证。文献[5]在标准模型下构造高效的口令认证密钥交换协议,但该协议不能抵抗量子攻击。文献[6]基于LWE构造了无环密钥交换协议,虽然该协议可以抵抗量子攻击,但无法实现客户和服务器的相互认证。文献[7]提出一个基于理想格的密钥交换协议,使通信方以显著概率计算得到一个相同的会话密钥,然而该协议提取的会话密钥只具有高熵,并不是均匀分布的,虽然通信方可以利用随机提取器得到均匀分布的共同比特,但这会降低协议的效率。文献[8]提出一种基于理想格的密钥封装机制(Key Encapsulation Mechanism,KEM),文献[9]在此基础上结合一种简单的低带宽协调技术提出一种变形的错误协调机制,结合环LWE困难问题构造密钥交换协议,使加密方案的密文长度缩短了近两倍,通信方可以直接得到均匀的共同比特。
文献[10]结合Peikert式错误协调机制构造了适用于TLS协议的Diffie-Hellman式密钥交换协议,并给出具体的实现参数,其中会话密钥能达到较高的量子安全级别,但错误协调机制模数较大,使得通信量较大,降低了协议的效率。文献[11]基于R-LWE困难问题,利用格解码算法结合中心二项分布提出了NewHope密钥交换协议,优化了文献[10]的密钥交换协议,扩大了可容忍的错误范围,减少了模数,节省了通信量。文献[12]提出的NewHopeSimple方案,使用加密的构造方法代替调和技术,降低了协议的计算复杂度。文献[13]基于加密的构造方法提出抗选择密文攻击安全的Kyber系列密钥封装算法,其采用密钥压缩技术对需要发送的公钥和密文进行压缩,降低了通信量。
随着格密码的快速发展,密钥交换协议的效率已得到大幅提高,但目前多数协议都是Diffie-Hellman式密钥交换协议[7,10,14-16],只能提供被动安全性,不能实现相互认证,也不能抵抗中间人攻击,而实际应用中必须要考虑网络上的主动攻击者。因此,构造认证密钥交换协议来抵御主动攻击是研究趋势所向,而基于KEM方案构造认证密钥交换协议是一种可行的方法。
文献[17]在NTRU格Diffie-Hellman式密钥交换协议的基础上,结合带消息恢复功能的签名算法与KEM方案实现协议的认证性。与传统签名算法相比,该方案既增加了安全性又提高了通信效率。文献[18]将具有CCA安全和CPA安全的KEM方案相结合,提出了适用于格的可认证密钥交换协议的通用架构,即GC协议,其将KEM方案作为基本的设计原语,在CK+模型下是可证明安全的。文献[19]提出的CCA安全的密钥封装机制,可由基本的CPA安全的密钥封装机制获得,使用这一方法,Kyber构造了具有认证性的密钥交换协议Kyber.AKE。文献[20]设计了格上基于R-LWE的三方PAKE协议,实现了通信方的显式认证,可避免两方认证密钥交换协议的局限性,但该协议存在会话密钥的不一致性问题。
为实现Diffie-Hellman式密钥交换协议的认证性并使其能够抵抗量子攻击,本文结合带消息恢复功能的签名算法,基于R-LWE构造一个KEM方案。在协议执行时采样随机种子生成协议双方的公共参数,防止攻击者利用固定公共参数攻击协议,以保证前向安全性。发送方选择定比特长的随机字符串,每4个元素使用Encode函数[12]编码其中的一个比特,编码后的环元素可容忍更大的错误,从而降低模数,缩减通信量。此外,在保证密文恢复完整性的前提下对密文元素使用Compress压缩函数进行压缩,减轻服务器的传输负荷,同时利用带有消息恢复功能的签名算法实现协议的认证性。
1 相关知识




1.1 密文压缩算法
密文压缩技术是减少用户通信量的有效方法,其对密文元素进行压缩,丢掉密文元素的低位比特,即部分噪音信息。在保证密文恢复完整性的前提下,有效减少通信量,减轻服务器的传输负荷。将密文元素从q映射到2d上,其中d 定义1一个密文压缩算法包括2个多项式时间算法,即压缩算法Compressq(x,d)和解压缩算法Decompressq(x,d)。 1)压缩函数: Compressq(x,d)=⎣(2d/q)·x」mod+2d 2)解压缩函数: Decompressq(c,d)=「(q/2d)·c⎤ 文献[14]提出带消息恢复的签名算法,其中每一个用户都有一对密钥,即一个需要公开的公钥和一个需要秘密保存的私钥。当用户需要对某个消息m进行签名产生对应的数字签名Sig时,即需要使用自己的私钥和消息m=(m1‖m2)进行签名运算,运算结果就是签名值。签名值只需要消息m中的部分消息m2表示。任何人都可以使用该用户的公钥来恢复消息和验证签名是否正确,并且没有人能够在用户私钥未知的前提下伪造出一个合法的消息签名对。此算法可解决签名消息过长的问题。 定义21个带消息恢复的签名算法包括3个多项式时间算法,即签名密钥生成算法SigKeyGen(1λ)、签名算法Sig((f,g),m=(m1‖m2))和验证算法Ver(h,σ=(s1,s2,m2))。 1)签名密钥生成算法SigKeyGen(1λ):{f,g←Df,h←f/gmodq}得到(Ks,Kv)=(g,h)。 2)签名算法Sig((f,g),m=(m1‖m2)):{t=(m1+F(H′(m)) modq‖H′(m))s1,s2←Ds满足(f/g)s1+s2=tmodq,得到σ=(s1,s2,m2)。 3)验证算法Ver(h,σ=(s1,s2,m2)):(t1‖t2)←hs1+s2modq,m1←t1-F(t2)modq,若(s1,s2)‖ 定义3[10]用户A选取v∈{0,1}n环元素k,即每4个q元素中编码v的一个比特,用户B根据收到的k′,取在{0,1,…,q-1}范围中的4个系数减去⎣q/2」,累积它们的绝对值,若得到的结果小于q则vi取1,否则取0。可容忍更大的错误,从而降低了模数,缩减了通信量。Encode函数和Decode函数的具体描述如下: Encode(v∈{0,1}n) 输入k 对于i从0到n-1循环执行: ki←vi·⎣q/2」; ki+n←vi·⎣q/2」; ki+2n←vi·⎣q/2」; 输出k 输入k′,对于i从0到n-1循环执行: 若t 否则k′i←0; 输出k′ 模型中会话密钥的安全性通过模拟者和攻击者之间的游戏定义。首先攻击者A选择一定数量的诚实参与者,通过提供攻击者以下查询来建模攻击者的能力: 3)Corrupt(i)。攻击者A通过此查询来腐化参与者i。要求被询问的协议参与者返回参与者i的长期私钥,同时称参与者i被腐化(Corrupted)。 通过模拟一个挑战者与攻击者之间的游戏定义AKE协议的安全性。游戏分为以下4个阶段: 第1阶段攻击者A可以进行任意除Test以外的查询,预言机并给出相应答案。 第4阶段攻击者A结束游戏,输出猜测值b′。 对于任意攻击者A,如果A赢得上述游戏的优势AdvA=|2Pr[b′=b]-1|是可忽略的,则称该认证密钥协商协议是安全的。 认证密钥交换协议包括2个阶段,即系统建立阶段Setup和会话密钥的协商阶段KeyExchange。 H1和H2分别是在{0,1}l1和{0,1}l2上的抗碰撞哈希函数,通信双方分别使用带消息恢复功能的签名算法,选取{f,g←Df,h←f/gmodq},生成自己的签名密钥对: SigKeyGen(1λ)→(KSA,KVA)=(gA,hA) SigKeyGen(1λ)→(KSB,KVB)=(gB,hB) 用户UA和用户UB通过交换公共信息来协商出一个共享的会话密钥,具体过程如下: 若按照上述协议执行,最终交易双方得到相同的会话密钥,即SKA=SKB,具体的交换过程如图1所示。 图1 格上基于KEM的AKE协议交换过程 若用户UA和用户UB诚实地运行协议,那么双方获得相同的密钥SKA=SKB成立。 证明:通过一系列得模拟游戏,证明通信内容不会泄露秘密的信息,并证明通信双方交换的密钥与随机数不可区分。设sid*表示测试会话标示符,攻击者A尝试区分会话密钥SK和均匀随机密钥SK′,定义攻击者A赢得游戏的优势为: Adv(A)=|Pr[b′=1|b=1]-Pr[b′=1|b=0]| 在签名方案的强不可伪造性下,此修改不会改变攻击者A的优势。一旦伪造文件被发现,不需要运行完整个协议,签名方案立即被破坏。同时,c的分布与其他一般分布不可区分,所以,猜测出c=bs′b+e″b+a×k的概率可以忽略。因为c=a(sas′b+k)+e″b+ea,根据引理2可知,sas′b+k的分布与χα的分布小于4ε,基本可以忽略,则游戏G1中c的分布接近游戏G0中c的分布,即A无法区分。若RLWEq,χ是困难问题,则: |AdvG1(A)-AdvG0(A)|≤negl(n) 定义标记CorrectGuess来表示是否sk→⊥解密失败或者sk1←sk2解密成功,模拟器P不会显式地计算CorrectGuess的值。有: 标记CorrectGuess对游戏G5的比特b′无影响,这两个事件是独立的:AdvG5(A)=AdvG4(A)/2。 在最后的游戏中,测试会话的会话密钥是真实随机的,因此与随机的情况没有区别:AdvG7(A)=0。 通过以上游戏,可知攻击者A的优势是可忽略的。证毕。 本节对所提出的格上基于KEM的认证密钥交换协议方案进行性能分析,性能主要体现在3个方面: 1)发送方选择定比特长的随机字符串,将这个随机字符串中每4个元素使用Encode函数编码其中的一个比特,编码后的环元素可容忍更大的错误,从而降低了模数,缩减了通信量。 2)使用Compress压缩函数,对密文元素进行压缩,在保证密文恢复完整性的前提下,有效减少通信量,减轻服务器的传输负荷。 3)利用带消息恢复功能的签名算法,对方案中发送消息进行签名,在发送的过程中,用户双方只需要发送消息的部分值,有效降低了传输过程中的通信量。 表1 AKE协议效率分析与对比 本文方案和所对比的方案均为标准模型下构造。由表1可以看出,在通信量方面,本文方案采用Encode函数和Compress压缩函数,大幅缩短了密文的尺寸,有效降低了通信代价,同时使用带消息恢复功能的签名算法,在保证协议认证性的同时,也降低了通信量,与文献[10]方案相比,本文协议不但可实现相互认证,降低了通信量同时避免使用计算复杂的调和机制而使用计算简单的加密机制,方案计算更加简洁高效。本文协议的封装和解封装采用R-LWE困难假设,与文献[6]相比,解决了密文尺寸过长的问题。 综上可知,与同类方案相比,本文方案具有较低的通信量,计算复杂度也在可接受范围内。因此,从方案的效率参数和计算效率分析,本文协议更具有实际应用价值。 认证密钥交换协议被广泛应用于互联网安全协议和传输层安全协议中,可有效提高实体间的通信效率。本文基于R-LWE困难假设,以加密的构造方法代替Peikert错误协调机制,提出一种基于KEM的认证密钥交换协议。将KEM和带消息恢复功能的数字签名相结合,实现协议的认证性,同时降低需要发送的签名密文长度,大幅减少通信量。利用格上基于R-LWE问题构造的密码系统具有密钥、密文尺寸小的优点,可提高AKE协议效率,并且有效抵抗量子攻击。本文方案基于R-LWE困难假设构造,而LWE的安全性较R-LWE更为稳健,下一步将考虑在维持较低通信量的情况下,基于LWE构造强安全的认证密钥交换方案。


1.2 带消息恢复的签名算法
1.3 Encode函数与Decode函数
1.4 AKE协议安全模型






2 算法设计及方案构造
2.1 系统建立阶段
2.2 会话密钥的协商阶段


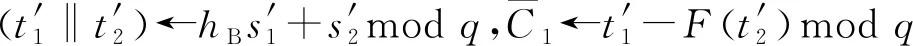

3 安全性分析
3.1 正确性证明

3.2 安全性证明
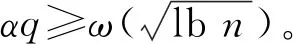










4 性能分析


5 结束语
