基于大跨径混合梁斜拉桥的粘滞阻尼器参数优化分析

陈 原

(四川省公路规划勘察设计研究院有限公司，四川成都 610041)

1 概述

结构保护系统，是上世纪最为伟大的科技成果之一。而其中发展最为迅速的，当属各种耗能阻尼器，其应用范围超过了我们的想象。1999年，阻尼器技术开始应用于桥梁工程结构中，并迅速发展。

目前，以粘滞阻尼器所构成的消能减震系统在各类大跨结构的抗震设计中应用广泛。这些大跨度桥梁往往在各个交通网络中起到非常重要的枢纽作用，在地震发生后，一旦桥梁受损，将给地震受灾地区的救援和恢复工作带来不可估计的损失。因此，提高大跨度桥梁的抗震性能一直以来是桥梁技术人员分析研究的重点。

随着粘滞阻尼器在我国桥梁工程的迅速发展，此类型阻尼器已成功应用于各类桥梁结构工程，包括鹅公岩长江大桥(2000年建成，主跨600m钢箱梁悬索桥)、上海卢浦大桥(2003年建成，主跨550m拱桥)、包树高速公路黄河特大桥(2011年建成，6×150m连续梁桥)、马鞍山长江公路大桥左汊桥(2013年建成，主跨2×1 080m悬索桥)、合福铁路铜陵长江大桥(2016年建成，主跨630m公铁两用钢桁梁斜拉桥)、丰都长江二桥(2017年建成，主跨680m钢箱梁斜拉桥)等。这些桥梁通常以轻质高强的钢结构主梁为主，对于跨径较大，且梁体较重的“混凝土-组合梁”的混合梁形式应用相对较少。本文以某跨江大跨径“混凝土-组合梁”混合梁斜拉桥为工程背景，研究通过在桥梁纵向设置粘滞阻尼器来提高桥梁纵向抗震性能，并就阻尼器的参数确定进行分析，得到的参数变化和分析方式可供该类工程应用参考[1]。

2 粘滞阻尼器的构造

粘滞阻尼器即一种消能构造，主要由缸体、活塞、活塞杆及阻尼介质构成[2]，具体如图1所示。

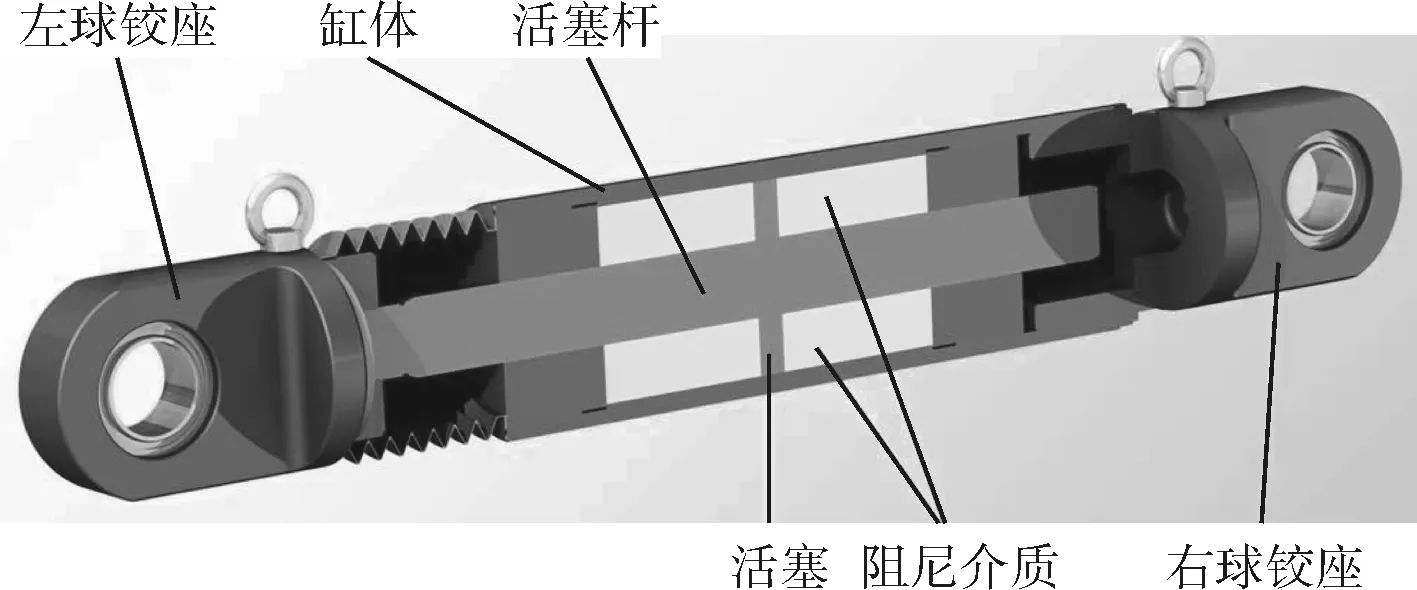
图1 粘滞阻尼器的基本构造

粘滞阻尼器对结构进行振动控制的原理为：通过缸体内活塞部分的往复运动激起缸体内阻尼介质流动而产生流动阻抗力(包括节流孔对阻尼介质的剪切阻抗)，从而减小结构在各种作用下引起的振动反应，达到消能作用。

粘滞阻尼器的力与速度的关系一般采用式(1)表达：

F=CVα

(1)

式中：F为阻尼力，单位kN；C为阻尼常数，单位kN/(m/s)α；V为阻尼器冲程速度，单位m/s；α为阻尼指数。

3 工程背景

3.1 工程概况

某跨江大跨度斜拉桥，位于宜宾市临港经济开发区。大桥采用主跨480m的混合式斜拉桥方案，即边跨采用双纵肋混凝土梁断面，中跨采用双钢箱梁组合梁断面，钢混结合段位于中跨索塔附近。主塔为钻石型桥塔配群桩基础，主塔总高约183m，其中上塔柱约134m，下塔柱约49m。边跨拉索标准间距8.5m，中跨拉索标准间距11.1m。

桥梁总长866m，主跨跨径480m，边跨跨径193m，边中跨比为0.402。单侧边跨设置2个辅助墩，设置辅助墩后的边跨跨径组合变为45m+51m+97m。中跨主梁标准宽度40m，边跨主梁为变宽，宽度范围40～57m。桥梁布置图及标准梁体断面如图2～图4所示。

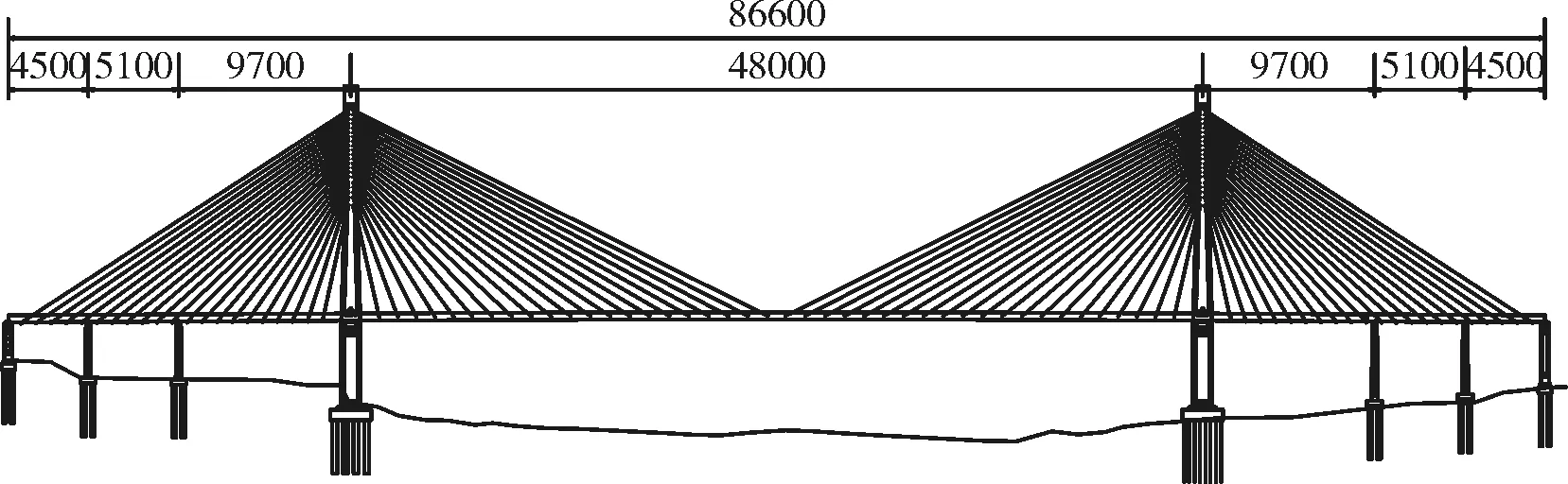
图2 桥型总体布置

图3 中跨组合梁断面

图4 边跨混凝土梁断面

3.2 计算模型

主桥结构抗震分析计算采用MIDAS/Civil三维有限元计算分析软件，其中主梁、主塔、桥墩、承台及桩基采用梁单元进行模拟，斜拉索采用桁架单元模拟，拉索弹性模量采用公路斜拉桥设计细则[3]中6.2.4公式进行修正，桩基根据地勘资料和地基规范，采用m法模拟土弹簧进行约束。粘滞阻尼器采用MIDAS自带的Maxwell模型进行模拟。

3.3 地震参数输入

地震参数的输入，采用该桥《工程场地地震安全性评价报告》中提供参数，选取50a超越概率2 %(即地震重现期2 475a，对应抗震规范的E2)的参数计算[4]。报告中针对此概率水平的地震作用提供了3组水平地震动加速度时程数据，其中一组数据如图5所示。

图5 加速度时程荷载 (函数单位：m/s2)

4 粘滞阻尼器计算分析

4.1 布设方案

纵向阻尼器的位置一般布设在两个具体位置：一是布设在梁端头交界墩或桥台位置；一是布设在主塔位置。此外，阻尼器的布设个数和位置一般采用对称偶数布置，通常为4个或者8个。

该长江桥考虑主塔结构较强，交界墩相对较弱。因此阻尼器仅布设在主塔位置。同时由于该桥梁宽度较宽，主梁整体重量较大，因此设置8个阻尼器进行计算分析。

4.2 参数选取

不同的阻尼参数直接影响了结构在地震作用下的不同反应，根据式(1)可知，影响结构地震作用得阻尼器参数主要在阻尼常数C及阻尼指数α，因此本文将根据以下不同取值进行结构地震响应对比，以确定适合该长江大桥的阻尼器参数(表1)。

表1 粘滞阻尼器参数取值

4.3 变形及内力分析

桥梁地震作用下的关键研究点，主要包括两个方面：一是结构关键部位的内力；二是结构在地震作用下的位移。该桥设置的阻尼器主要用于抑制纵桥向地震作用，纵桥向地震作用下的关键受力位置即为主塔塔底。同时，纵桥向作用下的桥梁关键部位位移分析主要为塔顶和梁端。因此，本文主要通过对比塔底内力、梁端及塔顶位移，来分析阻尼器参数对桥梁结构抗震的影响，同时结合阻尼器阻尼力的大小，最终确定该桥合理的参数大小。不同阻尼常数C及阻尼指数α的计算结果如图6～图11所示。

图6 塔顶纵向位移曲线

图7 梁端纵向位移曲线

图8 塔柱底纵向弯矩曲线

图9 塔柱底纵向剪力曲线

图10 塔柱底轴力曲线

图11 阻尼力曲线

设置粘滞阻尼器，在不同阻尼常数C及阻尼指数α的参数下，桥梁结构的地震响应有着较大差别。通过上述对比图形，可见：

(1)对比不设阻尼器的情况，在设有阻尼器的情况下，塔顶位移减小了41.5 %～71.2 %，梁端位移减小了42.9 %～74.4 %，塔底纵向弯矩减小了24.8 %～58.4 %，塔底纵向剪力减小了12.8 %～25.2 %，塔底轴力减小了5.6 %～13.2 %。设置阻尼器在内力及位移各项指标上，对桥梁结构抗震均有改善。

(2)阻尼常数C的增加，有利于桥梁结构地震响应。以阻尼指数α=0.3为例，阻尼常数C由2 000增加至3 500后，塔顶位移减小了31.0 %，梁端位移减小了33.8 %，塔底纵向弯矩减小了28.5 %，塔底纵向剪力减小了5.4 %，塔底轴力减小了2.4 %。但阻尼器最大阻尼力增加了56.9 %。

(3)阻尼指数α的减小，有利于桥梁结构地震响应。以阻尼常数C=2500为例，阻尼指数α由1.0减小至0.2后，塔顶位移减小了29.5 %，梁端位移减小了31.0 %，塔底纵向弯矩减小了32.8 %，塔底纵向剪力减小了6.0 %，塔底轴力减小了6.0 %，同时阻尼器最大阻尼力也减小了3.2 %。

(4)阻尼器设置于索塔横梁位置，阻尼器的最大阻尼力对索塔横梁的受力有影响，通过上述对比，综合考虑索塔受力、横梁受力及梁端伸缩缝的选取后，最终选用的阻尼器参数为阻尼常数C=2500kN/(m/s)α，阻尼指数α=0.2，最大阻尼力F=2500kN，最大阻尼行程S=600mm。在此参数下，塔顶及梁端位移分别下降了61.0 %及63.7 %，塔底的纵向弯矩、剪力及轴力分别下降了52.0 %、21.6 %及12.6 %。桩基边桩顶的轴力及弯矩也相应下降了49.5 %及16.9 %。

5 结论

本文针对某跨江大跨径“混凝土-组合梁”混合梁斜拉桥，在对比分析了不同的阻尼参数对桥梁地震作用的影响后，得出了以下结论：

(1)阻尼器能有效减小地震作用下该类桥梁的位移和内力，尤其对桥梁纵向位移及塔底纵向弯矩这两个关键指标的减小作用明显。

(2)阻尼指数α不变而阻尼常数C增加时，地震作用下桥梁的位移和内力随之减小，但阻尼器最大阻尼力随之增加。

(3)阻尼常数C不变而阻尼指数α增加时，地震作用下桥梁的位移和内力随之增加，而阻尼器最大阻尼力呈现出一定的反向抛物线形状，且α在0.2～1.0范围内可找出最大阻尼力的极小值。

(4)阻尼器设置于索塔横梁位置，阻尼力过大对索塔横梁的受力不利，由于阻尼指数对阻尼力的影响较小，而阻尼常数对阻尼力的影响显著，因此较小的阻尼指数配以合适的阻尼常数是比较合理的选择。

随着我国城市交通和“一路一带”的发展，将会有更多的城市桥梁和海外桥梁项目的建设。如何有效地减小桥梁结构在地震、大风作用下的动力效应，减少重大灾害下的人员和经济损失，更加科学高效地完成建设，值得我们仔细研究。本文对于阻尼器在此类桥梁上的应用分析，值得今后的同类工程参考。