圆柱和带圆弧圆柱绕流的二维数值模拟

2020-07-21陈立

四川建筑 2020年1期

陈立

(西南交通大学桥梁工程系，四川成都 610031)

圆柱绕流是流体力学中经典问题之一,因为流体具有一定的黏性,在一定雷诺数范围内,当流体流过固定圆柱时受到壁面的影响会发生边界层分离的现象,由此产生的漩涡会对圆柱产生周期性的气动力作用,这就是圆柱的绕流问题。对于圆柱绕流问题,国内外学者对其开展了较多的研究。Schlichting[1]根据圆柱绕流的实验结果绘制了阻力系数CD与雷诺数Re的关系曲线(Re范围1～107),发现CD在亚临界区比较稳定,此时稳定值大约为1.2。Simiu和Scanlan[2]通过对放入水洞中的圆柱体释放颜料,研究了流体随雷诺数增长的结构形态,发现在低雷诺数时(Re≈1),流体会附着在整个圆周上;在雷诺数Re≈20时,圆柱后端会形成两个对称分布的尾流漩涡;在5000≤Re≤200000范围内时,分离点后的尾流会由层流向湍流过渡。Shih[3]等人在高雷诺数(105≤Re≤107)下测量了不同粗糙度的圆柱的斯托罗哈数St,发现测量的St值大致保持不变,其值大约为0.2。

在城市中的斜拉桥,为了产生夜景的效果,会在斜拉索上安装灯具来实现亮化效果,通常采用在斜拉索表面固定线槽后,再将灯具安装在线槽上的方法[4]。其拉索截面可以简化为带圆弧的圆柱截面,这种截面的气动力特性较为复杂,容易导致风致振动。而在以往的文献中,很少有人对带圆弧圆柱的截面进行过绕流分析。因此本文,采用流体计算软件Fluent进行数值模拟,系统分析了圆柱和带圆弧圆柱的各种气动力参数,并且对比了其中差异,最后研究了带圆弧圆柱容易驰振的角度,对于深入认识流体的绕流问题以及改进工程结构设计有重要意义。

1 计算模型

1.1 控制方程

计算采用商业流体力学软件Fluent进行二维绕流模拟,湍流模型选用SSTk-ω模型。该模型增加了混合功能,即近壁区域标准k-ω模型有效,自由表面k-ε模型的变形有效。该模型还考虑了湍流剪应力的传播,采用更合适的模型常量与涡粘系数,这些改进使得SSTk-ω模型比标准k-ω模型在广泛的流动领域中有更高的精度和可信度。SSTk-ω模型的流动控制方程如下:

(1)

(2)

式(1)是湍流动能输送方程，式(2)为耗散率输送方程.在方程中,ui为时均速度,ρ为空气静压,k为湍流动能,ω为比耗散率,Gk和Gω分别为k和ω的产生项,Yk和Yω分别为k和ω的耗散项,Dω为正交发散项,Sk与Sω为用户自定义项。

1.2 模型和计算域参数

计算采用的拉索直径D为100mm,一种为纯圆形截面,目的是为了将计算结果与文献进行对比,以保证网格划分的正确性,并与另一种截面的拉索的计算结果进行比较;另一种拉索带有圆弧形凸起,圆弧弦长B为20mm,高H为10mm,见图1(a)。圆弧的位置用角度θ来定义,见图1(b)。

图1 圆弧大小与圆弧位置角示意

两种模型采用的的计算域见图2与图3,计算区域为圆形区域,为了使外边界足够远,计算区域的直径为3 200mm,为拉索直径的32倍,拉索中心与计算域中心重合。流体计算域左边为速度入口,流速设置为10m/s,湍流强度为0.5 %,湍流粘度比为2;右边边界设置为压力出口;圆柱表面设为无滑移壁面。

图2 圆形截面计算域与网格划分

图3 带圆弧圆形截面计算域与网格划分(θ=0°)

1.3 网格划分与验证

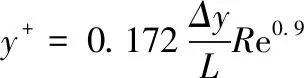
为了保证后续计算的可靠性,本文对网格和边界条件进行验证。首先对经典圆柱绕流的结果进行检查,截面为圆截面,流场的雷诺数设置为6.8×104,采用的湍流模型为SSTk-ω模型,压力速度解耦采用SIMPLE算法,时间步设置为0.001s。计算结果和文献[6]中的结果与实验结果[1]对比如表1所示。

表1 绕柱绕流计算结果对比

在采用二维模型来模拟圆柱绕流时,忽略了湍流对展向涡量的影响,且雷诺数越大这个影响也越大,因此计算所得到的升力、阻力系数和斯特劳哈尔数均会高于实验值,这在文献[7]里均有描述.在采用二维的SST模型时，本文计算结果与文献[6]基本一致,因此可以认为网格和边界条件的设置是可靠的,并且将该网格划分参数与边界条件应用于接下来的带圆弧圆截面网格划分中。

2 计算结果

2.1 流场分析

图4给出了圆柱与带圆弧圆柱的绕流流线图,从图4(a)可以看出,虽然圆截面具有对称性,但是流线上下是不对称的,这是由于在圆柱下游产生了周期性的漩涡脱落,且流线仅在发生涡脱的地方与表面发生分离。而从图4(b)和图4(f)中可以发现,当圆弧位置角θ为0 °或者是180 °时流线会一直附着在带圆弧圆柱的表面。从图4(c)、图4(d)和图4(e)中可以看出,当圆弧位置角θ为45 °、90 °、135 °时,流线会在抵达圆弧之前与表面分离,且θ为90 °与135 °时,分离后的流线会在圆弧表面发生再附。θ为45 °时,流线分离现象十分明显，而且分离后的流线并不会再附于带圆弧圆柱表面。

(a)圆柱附近流线

(b)带圆弧圆柱流线(θ=0°)

(c)带圆弧圆柱流线(θ=45°)

(d)带圆弧圆柱流线(θ=90°)

(e)带圆弧圆柱流线(θ=135°)

(f)带圆弧圆柱流线(θ=180°)

2.2 气动力系数分析

图5～图8给出了圆形截面和圆弧位置角分别为45 °、90 °、135 °的带圆弧的圆截面绕流的升力时程曲线、阻力时程曲线以及升力时程曲线的频谱分析结果。从升力时程曲线图中可以看出,两种截面的升力系数都呈周期性变化,但是随着圆弧位置角θ的增加,产生了不止一种的升力系数峰值,这说明带圆弧的圆柱随着圆弧位置角θ的变化会产生多个频率的漩涡脱落。从数值上来看,圆柱由于其对称性,其平均升力系数的值为0;由于圆弧的影响,带圆弧圆柱的平均升力系数均不为0,其值分别为:θ=45°时,CL=0.875;θ=90°时CL=0.223;θ=135°时,CL=0.486;从阻力时程曲线图中可以看出,圆柱的平均阻力系数为1.41。水线位置角为90 °时,带圆弧圆柱的平均阻力系数CD=2.06大于圆柱的值。而当水线位置角为45 °和135 °时,带圆弧圆柱的平均阻力系数分别为1.034和1.209均小于圆柱的值.从图7(b)和图8(b)中可以看出,当水线位置角为90 °和135 °时,阻力时程明显包含了多个频率的成分。

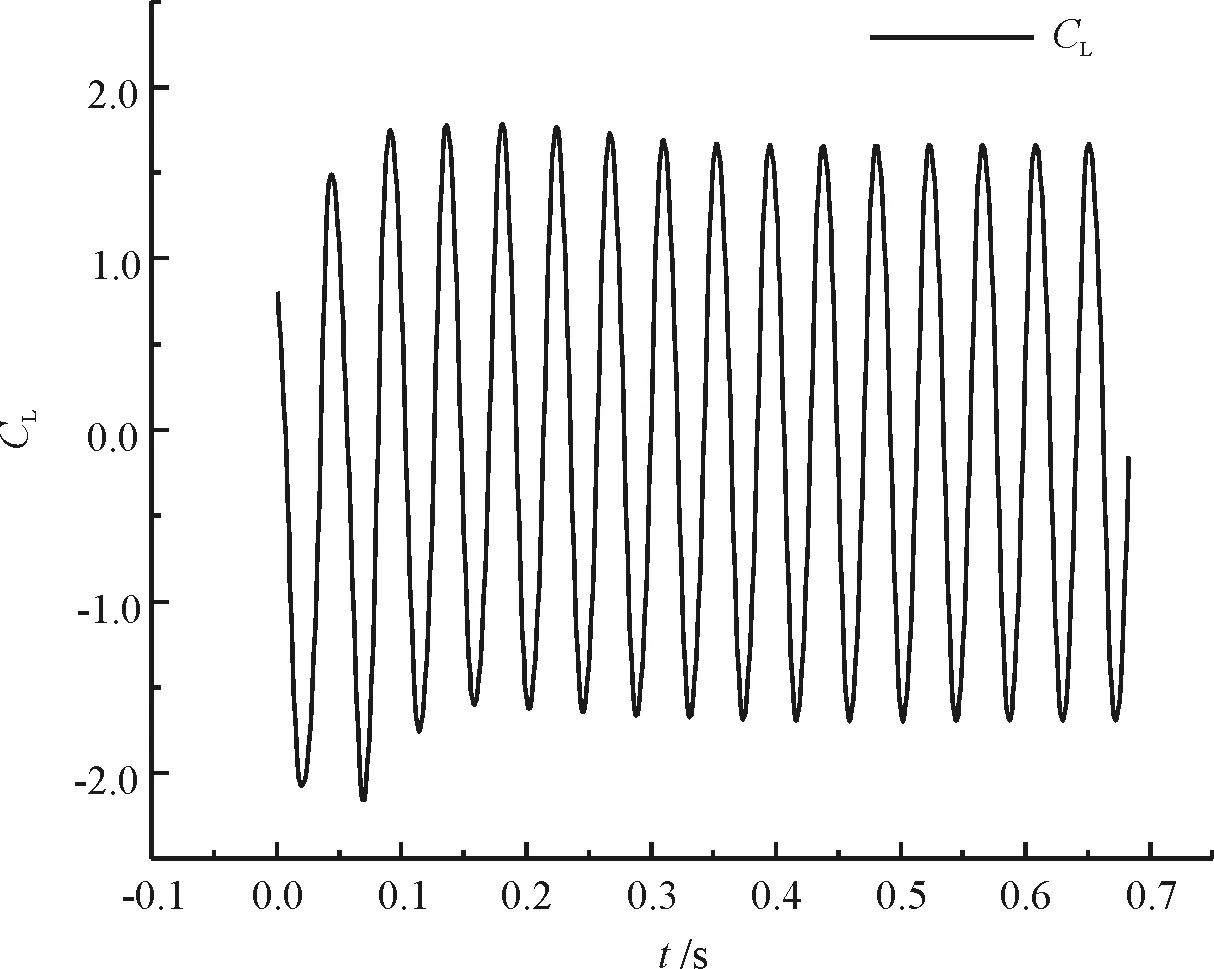
(a)升力时程曲线

(b)阻力时程曲线

(c)升力时程曲线的频谱分析

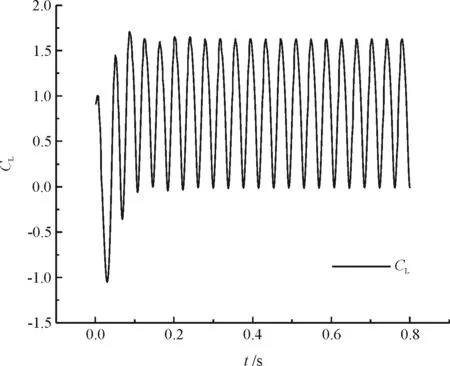
(a)升力时程曲线

(b)阻力时程曲线

(c)升力时程曲线的频谱分析

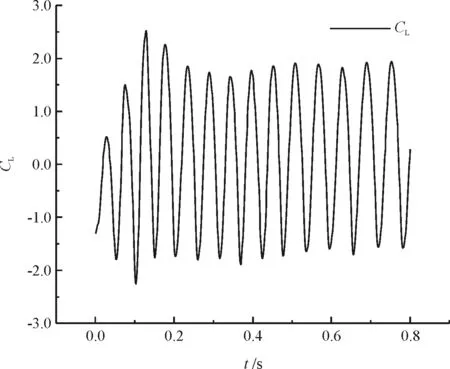
(a)升力时程曲线

(b)阻力时程曲线

(c)升力时程曲线的频谱分析

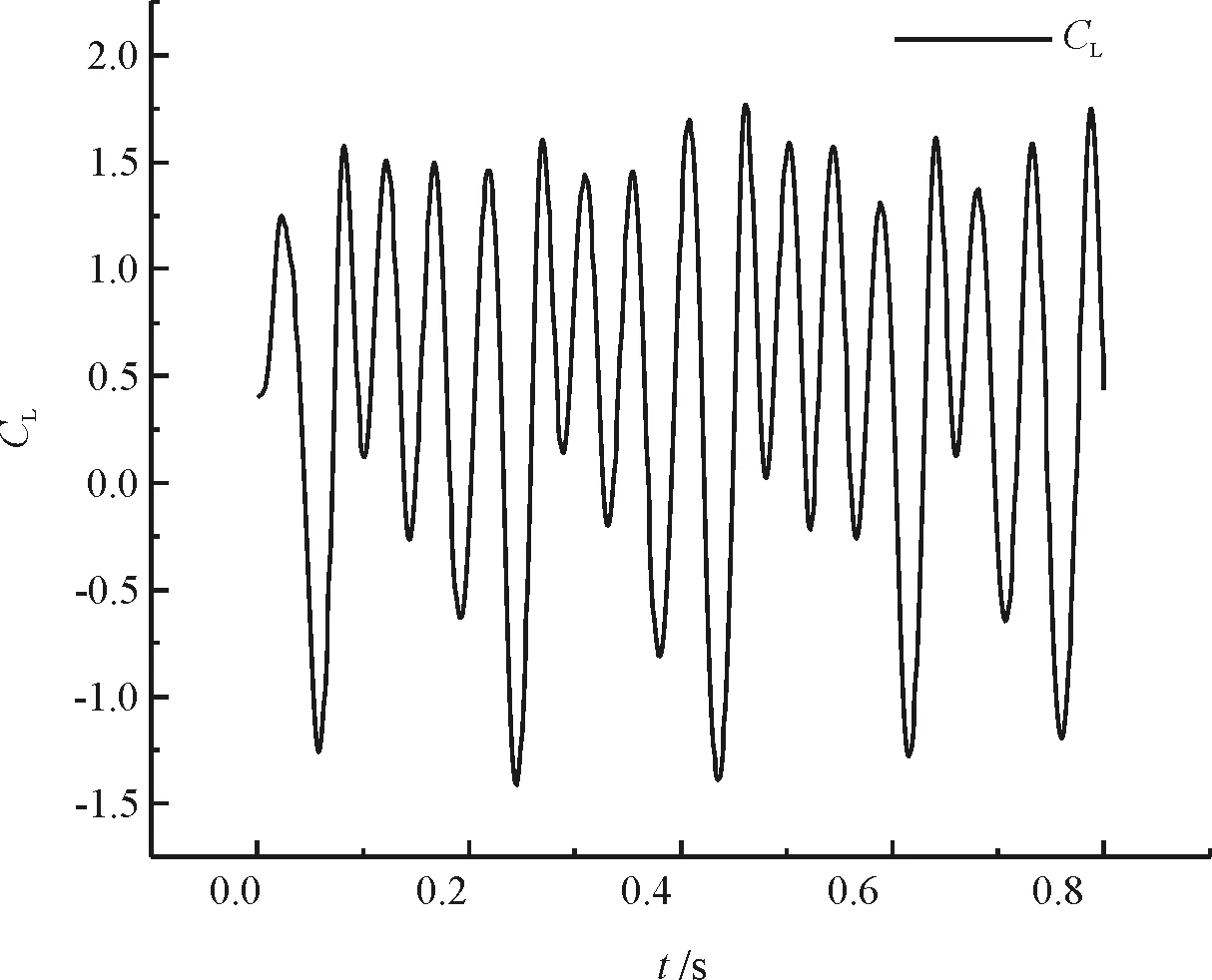
(a)升力时程曲线

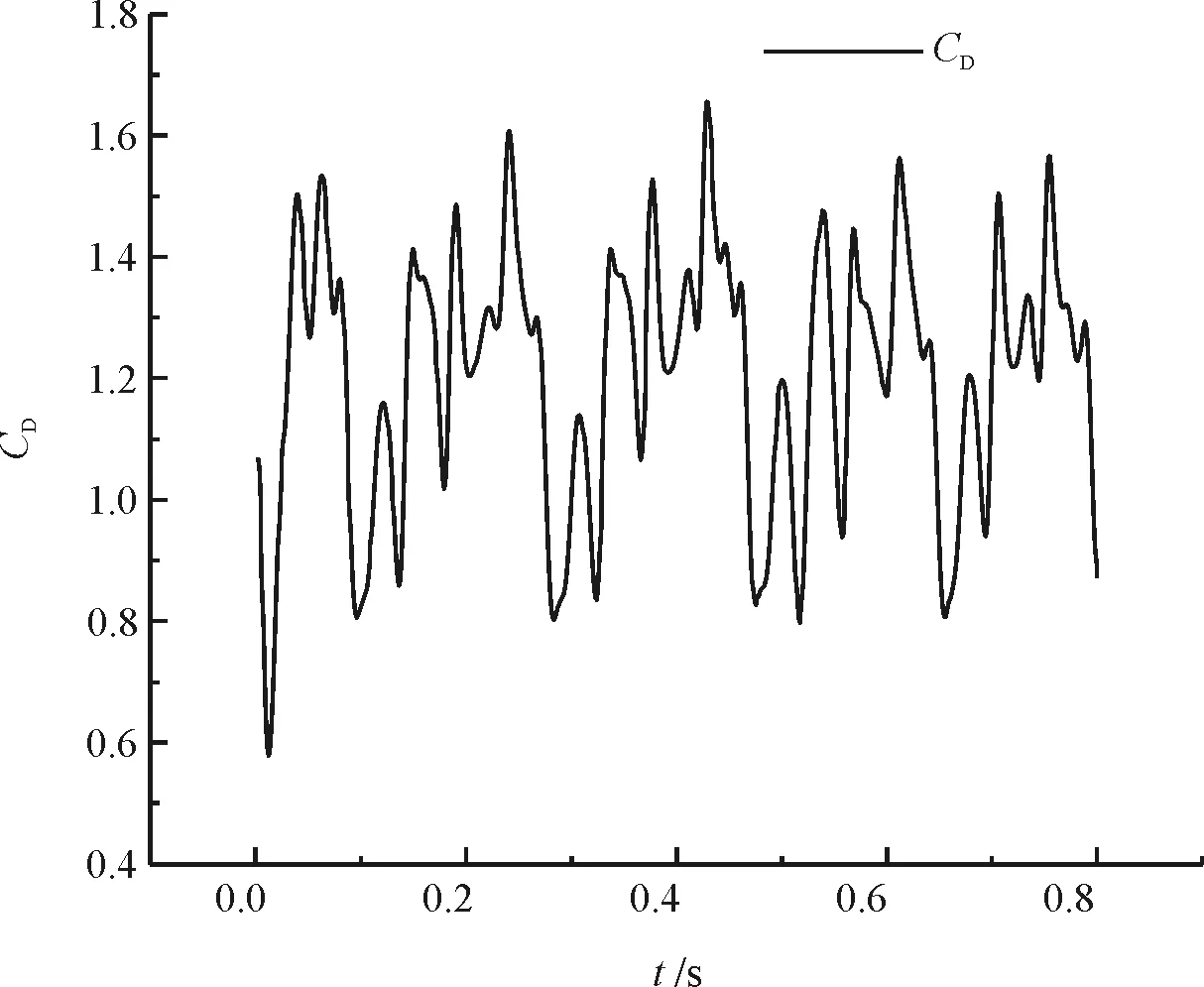
(b)阻力时程曲线

(c)升力时程曲线的频谱分析

通过对比升力时程曲线与阻力时程曲线可以发现,圆柱的阻力系数主频是升力系数主频的两倍,这在圆柱绕流的数值模拟中已有相同结论[10]。而带圆弧圆柱的阻力系数主频和升力系数主频相同,这是因为带圆弧圆柱不具有上下的对称性导致一个周期的涡脱会产生一个周期的阻力系数的变化。

从升力时程曲线的频谱分析图中可以看出,圆柱的斯托罗哈数St=0.234;当水线位置角变化时,带圆弧圆柱的斯托罗哈数分别为:θ=45°时,St=0.260;θ=90°时St=0.175;θ=135°时,St=0.213。可见,圆弧的存在和圆弧位置角都会改变拉索的涡脱频率特性。

图9给出了带圆弧圆柱的平均阻力系数和平均升力系数随圆弧位置角的变化曲线。从图9中可以看出,带圆弧圆柱的平均阻力系数曲线呈中间高两端低的突起形状,在圆弧位置角θ=45°时平均阻力系数开始上升,直到θ=100°时达到最大值,最大值为2.289,之后平均阻力系数开始下降,直到θ=140°下降的趋势停止.在0～45 °和140～180 °之间时平均阻力系数的值都相对较低,且变化比较平缓,系数值约为1.1左右。带圆弧圆柱的平均升力系数曲线形状为M形,当圆弧位置角θ=0～40°时,平均升力系数变化不大,并且数值都很小,系数值约为0.05。θ=45°时,平均升力系数突然达到了一个峰值,系数值为0.875。在θ=75°～110°时,平均升力系数比较稳定,系数值在0.23左右.之后平均升力系数开始上升,在θ=140°时达到第二个峰值,其值为0.573。之后开始慢慢下降,直到θ=165°时曲线变得平缓,在θ=180°时,平均升力系数变为0。