不排水条件下临坡地基破坏模式与承载能力分析

吴 迪， 程 明

(1. 西南交通大学土木工程学院，四川成都 610031； 2. 高速铁路线路工程教育部重点实验室，四川成都 610031)

在实际工程中由于地形或工程条件限制，需要在既有建筑附近进行基坑开挖，或者需要将建筑物建于边坡附近。此时为了保证建筑基础的稳定，需要考虑边坡对地基承载能力的削弱。因此临坡地基极限承载力是一个具有实际意义的岩土问题，但目前还没有完善的解决。

分析临坡地基极限承载力既需要考虑边坡的稳定，也需要考虑地基承载能力。两个问题的杂糅使得问题变得较为复杂。Meyerhof[1]研究发现，在条形荷载下，当坡高较低时临坡地基破坏机制为承载破坏，坡高较高时破坏机制为边坡稳定破坏。Georgiadis[2]分析了临坡地基在不同边坡条件和土体强度参数下的破坏机制，并对影响因素进行分析。国内也有大量的学者[3-6]通过极限平衡法或者极限分析法对临坡地基极限承载力问题进行了研究。但两种方法均需要提前假定破坏面，不能准确的反应临坡地基承载与稳定两种破坏机制的耦合问题。刘文红[7]对条形荷载下不排水土坡破坏模式判定及极限承载力进行了研究

考虑在不排水条件下，采用有限元计算分析临坡地基的破坏机制；研究不同土体黏聚力、荷载位置、边坡高度组合情况下，临坡地基极限承载力及破坏模式变化规律。

1 有限元计算模型及验证

1.1 有限元计算模型及网格划分

临坡地基极限承载力的大小由土体性质及边坡形状决定，主要参数为土体容重γ、黏聚力c、内摩擦角φ、边坡高度H、荷载宽度B、距离比系数λ(基础外侧边缘距坡顶距离/基础宽度)(图1)。在不排水的条件下，内摩擦角φ=0，因此可以不考虑。

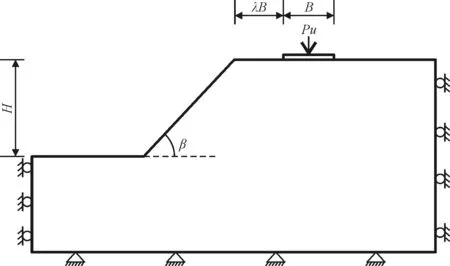
图1 计算模型示意

为了更方便地分析各种因素对于斜坡地基承载力的影响，在此将极限承载力以及相关尺寸表示为无量纲形式。

式中：P为极限承载力；c为土体黏聚力；φ为土体内摩擦角；γ为土体容重；H为边坡高度；β为边坡坡度；B为条形荷载宽度；λ为距离比系数。

运用PLAXIS2D软件建立有限元数值模型进行分析。考虑到条形基础的长度方向尺寸远大于横截面尺寸，属典型平面应变问题，因此计算模型采用二维模型。模型侧边采用水平约束，底边采用水平及竖直双向约束，顶面及坡面为自由面。为了简化分析，将边坡视为理想弹塑性材料的均质土坡，服从Mohr-Coulomb屈服准则，条形荷载作用于板单元几何模型网格划分首先采用全局网格划分，再对条形基础荷载、坡脚处进行网格加密，将几何模型划分为若干个 15 节点的三角形有限元单元网格(图2)。

图2 网格划分示意

由于计算模型有斜坡存在，计算采用重力加载法来附加土体重力引起的自重应力。重力加载为塑性计算中的一种，在重力加载过程中，将根据土的体积重度生成初始应力，如果选择重力加载，则会在重力加载工序中施加土的自重生成初始应力。使用重力加载生成初始应力后，在附加荷载工序中重置位移为零，删除初始应力生成过程中所产生的位移，重置位移后，应力依然保留。在工程实际中，岩土的破坏往往是一个渐进性的破坏过程，岩土体是由初始的线性弹性状态逐渐过渡到塑性流动的极限破坏状态的。因此可以采用增量加载的方式求解地基的极限承载力。随着荷载的逐步增加，岩土体由弹性逐渐过渡到塑性，最后达到极限状态，这时对应的荷载就为所要求的极限荷载。

1.2 有限元计算模型验证

对于不排水条件下(纯黏性土)条形荷载水平地基极限承载力，Meyerhof[1]提出了如式(1)所列承载力方程。

P=cuNc

(1)

式中：cu为纯黏性土粘聚力，Nc为承载系数。当边坡坡度β为0时，Nc=π+2。

将不同条件下下，采用PLAXIS2D计算结果与Georgiadis计算结果进行对比如图3所示，可以看出结算结果吻合。当λ足够大时Nc=π+2，与水平地基情况下的黏聚力参数一样大。因为当荷载位置足够远离边坡时，地基承载能力不再受边坡影响，次结论与Meyerhof一致。因此所采用计算方法具有可靠性。

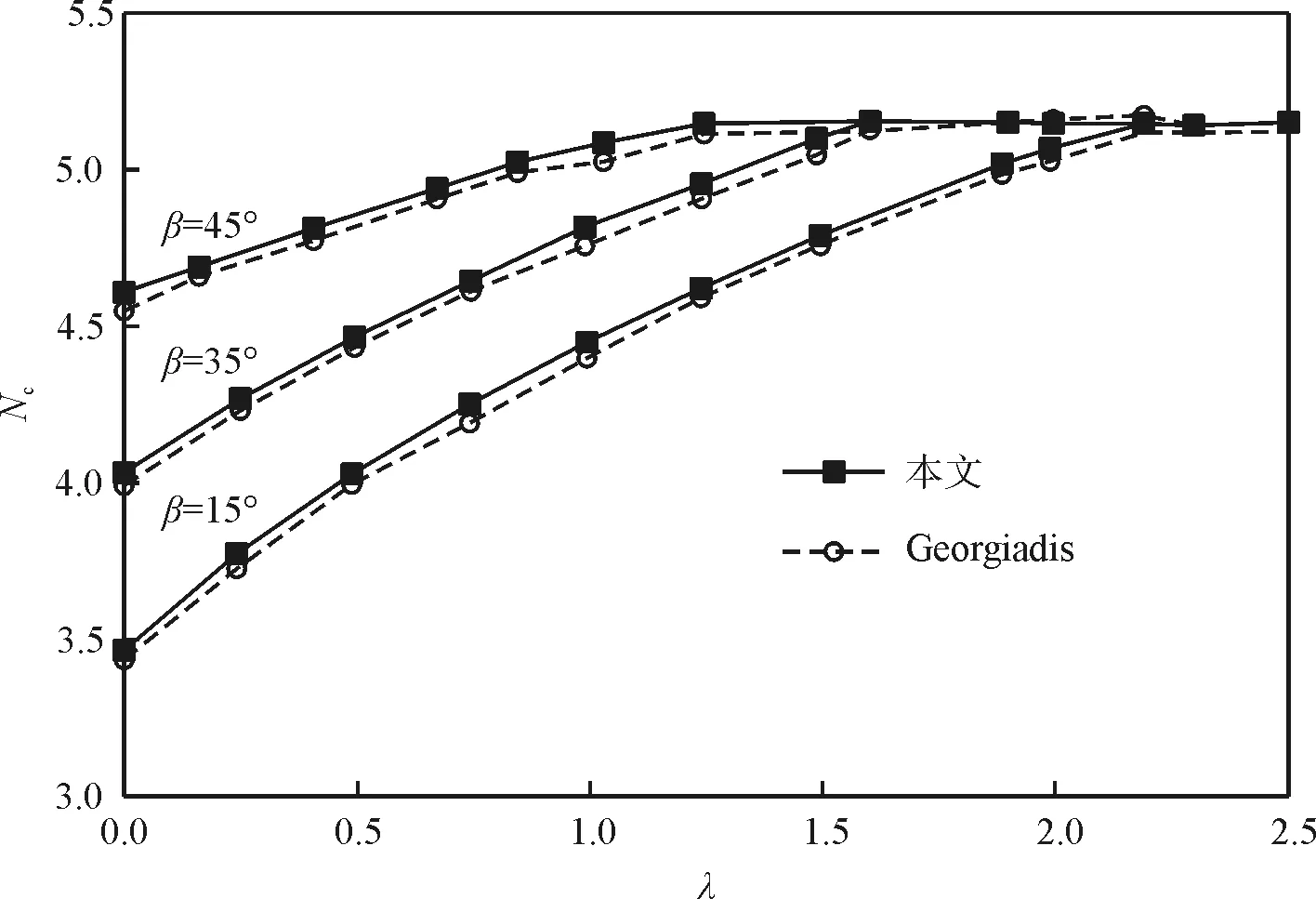
图3 黏聚力承载系数Nc对比

2 临坡地基破坏模式及影响因素分析

由于临坡地基问题是边坡稳定与地基承载的耦合作用，边坡对临坡地基承载能力的削弱作用体现在：

(1)由于边坡的几何条件，破坏区域减少引起抗滑力降低，破坏主导因素为外部荷载作用，破坏机制为承载破坏；

(2)当边坡稳定性不足时，破坏面趋近于边坡自重引起的稳定潜在滑动面，此时破坏区域朗肯被动区消失，因此抗滑力降低，引起破坏的主要原因为边坡土体自重的负面影响，破坏机制主要为稳定破坏。

据此可以将临坡地基破坏模式分为3类(图4)。当边坡不受边坡稳定影响，边坡高度较低时，滑动区域发展至地基面以下，被动区可以提供较大抗滑力，为图4(a)地基承载破坏，当边坡足够高，破坏面不再延伸至地基面以下，从坡面滑出为图4(b)边坡承载破坏。当边坡受边坡稳定性影响时，滑动面从坡脚滑出，破坏机制与边坡稳定破坏类似，为图4(c)边坡稳定破坏，边坡对临坡地基承载力削弱作用更明显。

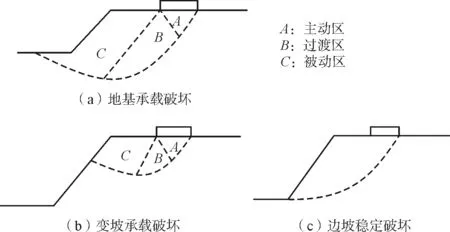
图4 破坏模式示意

2.1 黏聚力的影响

用cu/γB来为分析黏聚力cu对临坡地基极限承载力与破坏模式的影响规律，计算λ=1时极限承载随cu/γB变化规律如图5所示。

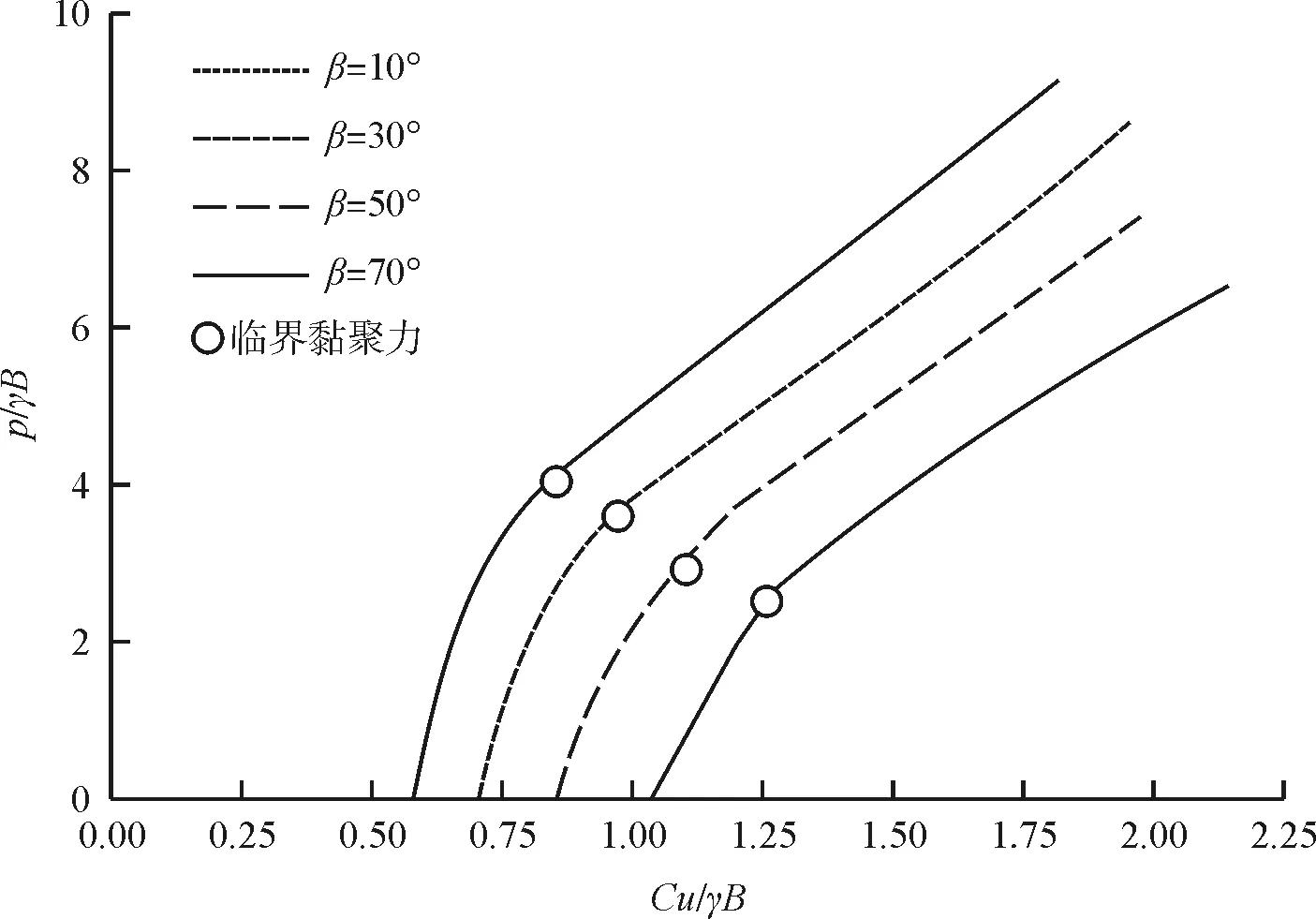
图5 极限承载力p/γB随cu/γB变化规律

可以看出临坡地基地基极限承载力随黏聚力增加而增加，且可以分为曲线段和直线段两个阶段。曲线与横坐标交点为边坡安全系数Fs=1时对应的黏聚力。此时边坡处于极限稳定状态，其承载能力为0。随着黏聚力增加，极限承载随黏聚力变化呈曲线变化，破坏模式为边坡稳定破坏。地基承载能力受边坡稳定性不足的负面影响，破坏面从坡脚滑出，承载力削弱明显。随着黏聚力增加，边坡稳定性逐渐提高。地基承载能力受边坡稳定性影响程度逐渐降低，至到黏聚力达到临界黏聚力，极限承载力开始随黏聚力线性增加。此时破坏模式如图所示，临坡地基承载能力不再受边坡稳定性控制。

2.2 距离比系数λ的影响

计算临坡地基极限承载随距离比系数λ变化规律如图6所示。可以看出随着条形荷载位置远离坡肩(即λ增大)，临坡地基极限承载力明显增大。当λ达到一定大小后，临坡地基极限承载力不再继续增加，定义此时的λ0为临界距离。达到临界距离后，临坡地基承载问题等同于相应土体强度下水平地基极限承载问题。极限承载力大小与边坡坡度无关，由土体黏聚力决定。

如图7所示，当cu/γB=1时，在β=30°时，临坡地基破坏模式为边坡承载破坏，β=45°、60°时破坏模式为边坡稳定破坏；当cu/γB=5时均发生边坡承载破坏。对比两种不同破坏模式下，极限承载力随λ变化情况，可以发现在承载破坏情况下，极限承载力增加速度比稳定破坏时要快，且更容易达到临界距离。

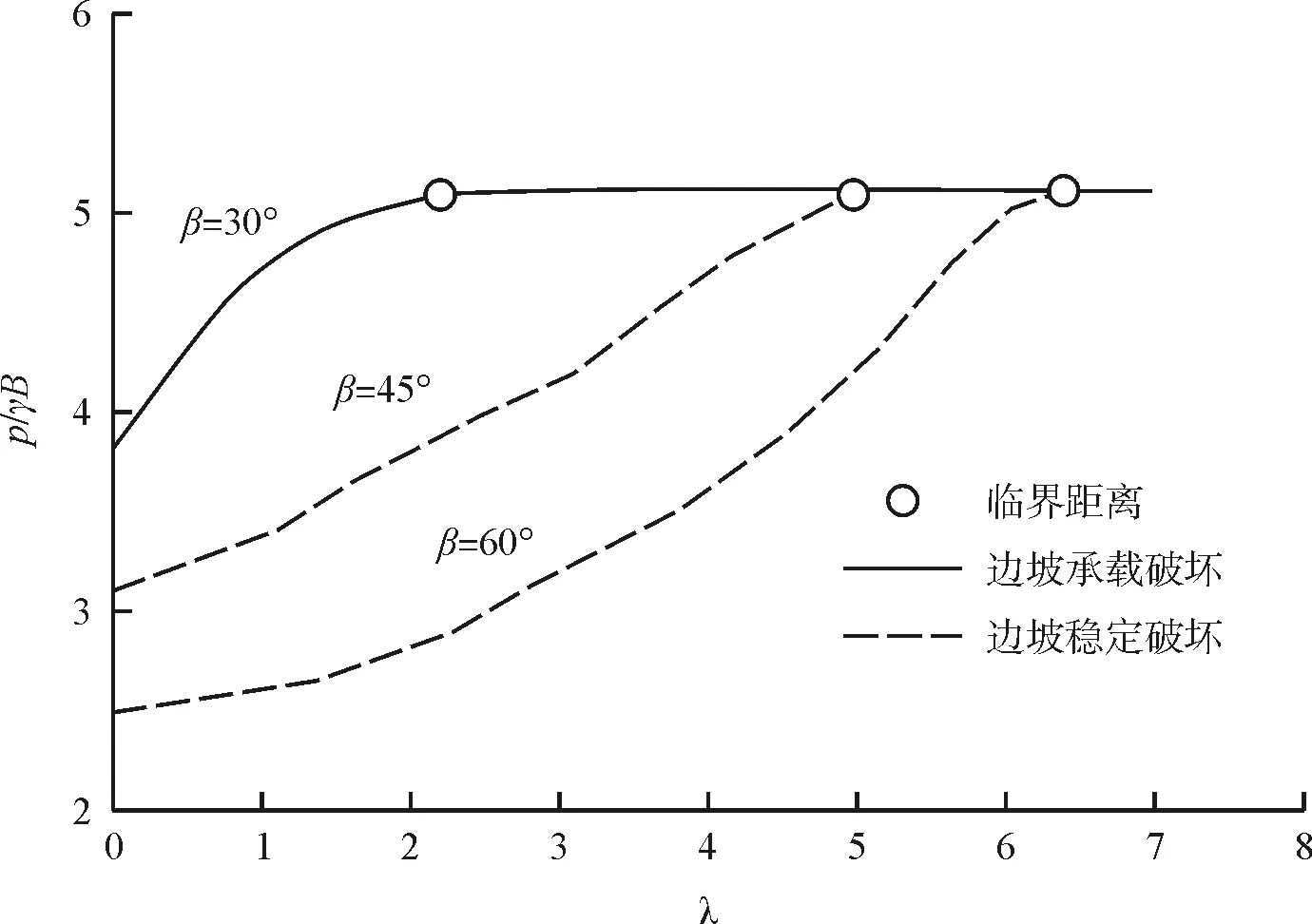
(a) cu/γB=1

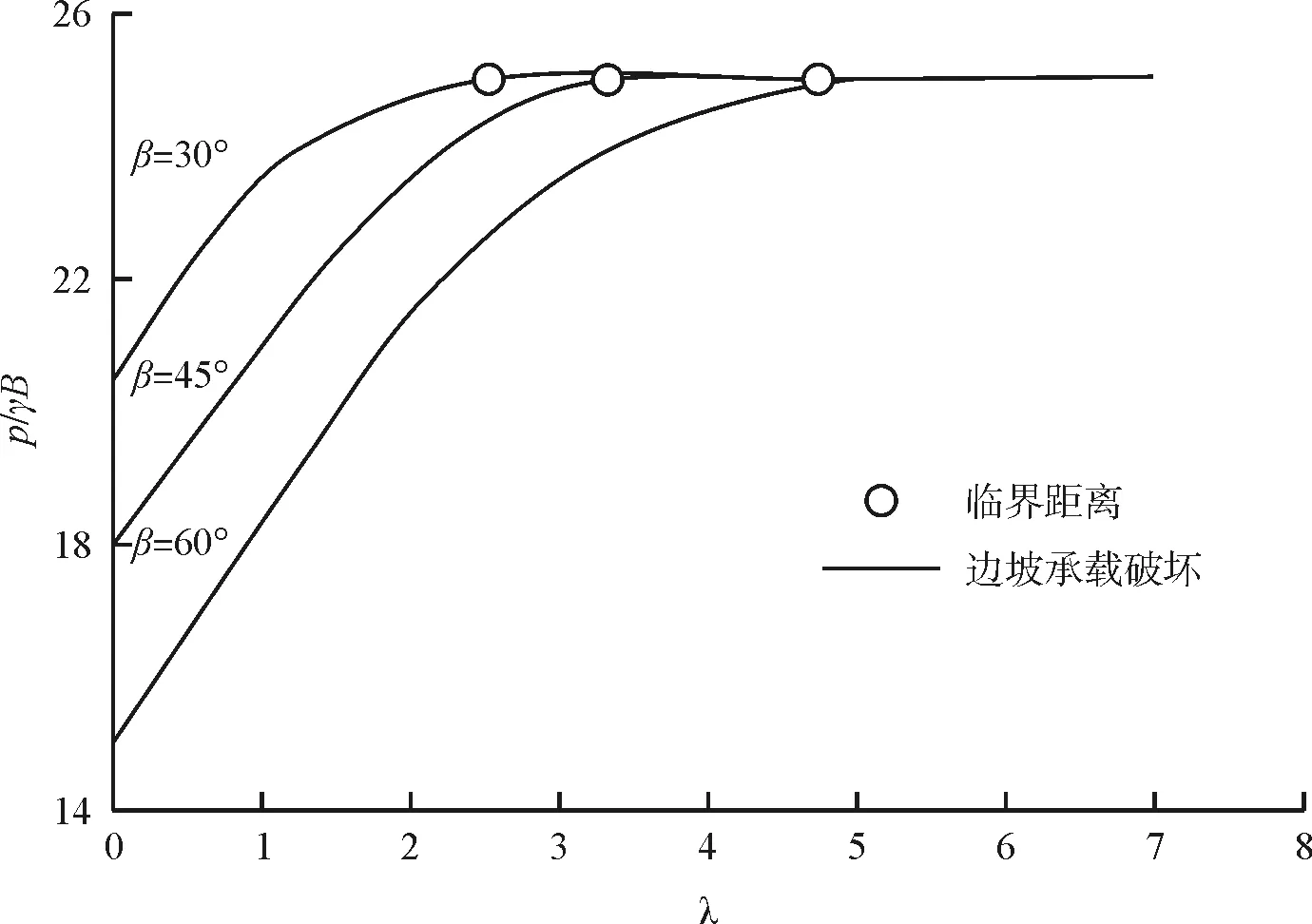
(b)cu/γB=5 图6 Nc随H/B变化规律

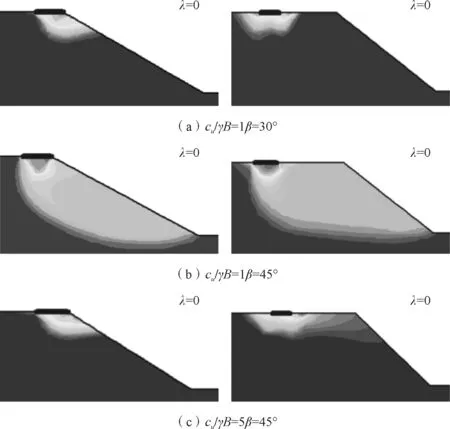
图7 破坏模式位移增量

2.3 边坡高度H的影响

由于P=cuNc，承载力系数Nc随坡高的变化可以反映出边坡高度对临坡地基承载能力的削弱作用。计算分析cu/γB=0.5、1.0、1.5三种情况下，H/B对临坡地基极限承载力的影响规律(图8)。

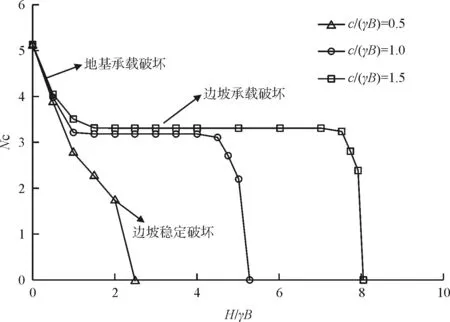
图8 Nc随H/B变化规律

当H/B=0时，无论cu/γB取何值，Nc均为5.14(≈π+2)，地基承载能力不受边坡影响，等同于水平地基。H/B≤1.5时，破坏模式为地基承载破坏，临坡地基极限承载力急剧降低。在这种破坏模式下，随着坡高的增加，破坏区域侵入地基面以下部分逐渐减小，抗滑力明显降低。随着坡高继续增加，cu/γB=0.5时，破坏模式转变为边坡稳定破坏，承载能力继续降低。当cu/γB=1.0或cu/γB=1.5时，边坡稳定性相对较高，表现的破坏模式为边坡承载破坏，承载能力在一定范围内不受边坡稳定性影响，因此极限承载不随坡高变化。但是随着H/B继续增加，边坡稳定继续增加，cu/γB=1.0、1.5两种情况分别在H/B=4.1和H/B=7.2时边坡模式坡面承载破坏转变为边坡稳定破坏。随着H/B继续增加，最终临坡地基极限承载力减为0。即边坡达到极限稳定状态，不再具有承载能力。

3 结论

采用有限元方法，对不排水条件下临坡地基破坏模式及极限承载力随黏聚力cu、荷载位置λ、边坡高度H/B变化规律进行了研究，结论如下：

(1)根据破坏机制与破坏区特征，可以将临坡地基破坏模式分为地基承载破坏、边坡承载破坏、边坡稳定破坏三类。

(2)随着黏聚力增加，临坡地基破坏模式由稳定破坏向承载破坏转变。发生承载破坏时，极限承载力随黏聚力呈线性增加。

(3)距离比系数λ达到临界距离λ0时，临界地基极限承载力不再增加。相比于模式为承载破坏，当临坡地基发生边坡稳定破坏时临界距离λ0显著增加。

(4)临坡地基破发生地基承载破坏或边坡稳定破坏时，极限承载力随边坡高度增加锐减，发生边坡承载破坏时，边坡高度对极限承载力没有影响。