周期性轨道缺陷态研究

柯文华， 李 祥， 魏 晓

(1. 高速铁路线路工程教育部重点实验室，四川成都 610031； 2. 西南交通大学土木工程学院， 四川成都 610031)

近些年我国轨道交通快速发展，列车运行速度和密度都在不断提高，轮轨之间的相互作用也随之不断加剧，由此引起的环境振动与噪声问题逐渐进入人们的视野，得到越来越多的重视。轨道作为一种向上承载列车荷载、向下传递轮轨作用力的结构，它的振动传递特性在解决轨道交通引起的环境振动与噪声问题中显得尤为重要。

为了方便施工与养护维修，轨道通常被设计成一种周期性结构，最明显的就是扣件呈现一定距离的周期性排列。以钢轨-扣件系统为研究对象，可将钢轨考虑成周期支撑梁模型，将最小的周期单元称为元胞，轨道结构的元胞如图1所示。

图1 周期轨道结构

近代固体物理学研究发现周期结构具有重要的物理特性，即衰减域特性，又称之为振动带隙特性：当振动在周期结构中传播时，某些频率范围内的振动不能通过，则这些频率段称之为带隙或禁带；而某些频率范围内的振动可以通过，称之为通带[1]。

由于轨道结构存在周期性，而周期结构又具有带隙特性，因此有许多学者以周期结构带隙理论来研究轨道结构的振动特性。

西南交通大学王平老师在文献[2]中运用传递矩阵方法和Bloch理论，通过Matlab编程计算，发现在周期性支撑的轨道结构中存在带隙。易强利用U变换法计算2种具有无限长周期轨道特征的轨道模型在静荷载作用下的精确解[3]。孟铎基于局域共振原理研究轨道周期性结构振动特性，并在轨道上周期性附加吸振器，研究周期结构带隙特性在轨道减振中的应用[1]。陈代秀运用ANSYS建立车-轨耦合模型发现扣减的周期性布置对轮轨力有一定的影响[4]。

以上研究均表明扣件周期性支撑会使轨道结构振动时存在带隙，但都是针对严格周期轨道结构而言的，现实运营路线经常会出现弹条断裂、轨下橡胶垫板失效等情况，破坏轨道结构严格的周期性，这样必然会对轨道结构的振动特性带来一定的影响，因此本文基于Bloch定理，结合超元胞理论，用有限元计算方法，建立含缺陷的周期性轨道结构超元胞，研究扣件受损或失效对周期性轨道结构带隙特性的影响。

1 有限元法轨道结构缺陷态计算

解析解模型都过于简化和理想化，与现实情况相差较大，而有限元算法能考虑复杂的边界条件，使计算结果更加接近现实，而且可利用现有的专业软件如ANSYS、ABAQUS等，操作方便，已有学者运用有限元法对周期结构的动力学特性进行过相关研究[5-8]。由于以上优点，本文采用基于ANSYS的有限元方法进行建模计算，钢轨和扣件分别采用beam4梁单元和弹簧单元进行模拟，模型如图2所示。

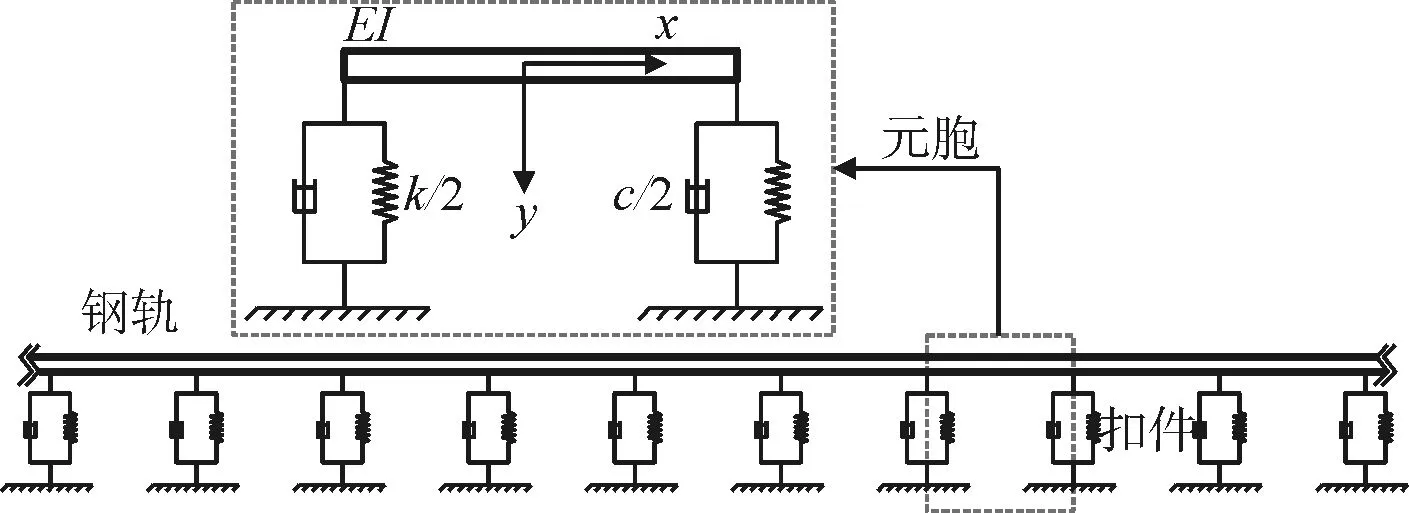
图2 模型示意

对包含任意N个元胞的周期轨道结构应用有限元方法离散后可得到广义特征值方程：

KU=ω2MU

(1)

该方程可缩聚到一个元胞子结构中[9]，因此运用有限元法研究周期结构的动力学只需对单个元胞子结构进行分析，在整个结构中提取单个元胞，采用有限元技术将单个元胞进行离散化处理，然后根据周期元胞之间的边界条件，运用Bloch定理对其进行处理，可以得到相对应的各个振动模态[10]。

将图1虚线中的单个元胞提取出来如图3所示。

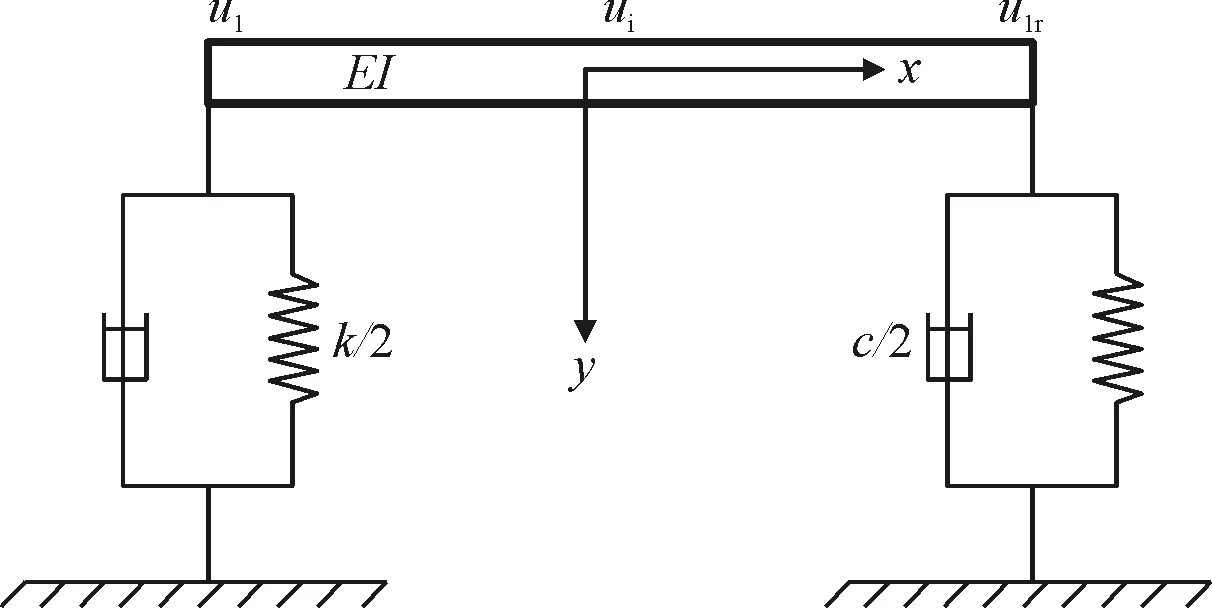
图3 单个元胞示意

该元胞的运动方程可表示为：

(k-ω2m)u=F

(2)

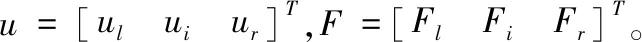
根据Bloch定理，周期结构元胞的边界点之间的位移和力之间存在如下关系：

ur=ulei(qk·a)Fr=-Flei(qk·a)

(3)

式中：qk表示波矢，a表示元胞长度，即扣件间距，可得：

u=AuBF=BFB

(4)

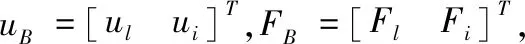
(5)

将式(5)代入式(2)后得到：

(k-ω2m)AqB=BFB

(6)

式(7)两边乘A的复共轭转置矩阵AH，又Fi=0，可得：

(7)

式(7)是一个典型的矩阵特征值问题。特征值问题的形成与求解还依赖于边界条件的处理，将节点位移写成复数形式，即：

u=uR+iuI

(8)

上标I、R分别代表实部和虚部。

将式(8)代入式(3)，又ei(qk·a)=cos(qk·a)+isin(qk·a)，可得：

(9)

求解关于周期结构的Hermitain特征值问题就转换为求解在式(9)约束条件下单个周期子结构的特征值问题。由于特征值方程分成了实部和虚部，所以需要建立两个完全相同的元胞子结构有限元模型。在通用有限元软件ANSYS中建立频率提取分析步，沿不可约Brillouin区边界选取波矢，分别求解每个波矢对应的特征值，就可以得到能带结构ωn(k)。取多个元胞子结构组合成超元胞，在超元胞中引入受损扣件，以此超元胞计算含缺陷的周期轨道结构带隙特性。

2 有限元模型计算结果

钢轨采用CHN60轨，截面面积为7 745 mm2，截面惯性矩为3.217×10-5m4，弹性模量为210 GPa，扣件间距a=0.625 m，扣件刚度取值如下表1所示：

表1 扣件刚度参数

取30个元胞组成超元胞，受损扣件位于正中间，根据理论推导部分可知，需要建立两个完全相同的元胞子结构有限元模型分别代表特征方程的实部和虚部，图中的上面那条线代表实部模型，下面的代表虚部模型(图4)。

图4 模型示意

由于在横向振动分析时,梁模型无法反映钢轨于轨头处横向激励引起的扭转变形,计算结果与实体模型差别较大，而且钢轨从1 200Hz开始会发生较大的截面变形振动，Beam4梁单元无法模拟这种截面变形[11]，故本文只研究1 200Hz内钢轨垂向与纵向振动，通过分别改变扣件垂向刚度kv和纵向刚度kl来简单模拟扣件受损，以研究这种缺陷对轨道结构振动的影响。

2.1 改变垂向刚度

Kv依次等于Kv,0、0.75Kv,0、0.5Kv,0和0，其中Kv,0为扣件正常垂向刚度，不同扣件刚度下钢轨垂向振动的能带曲线如图5所示。

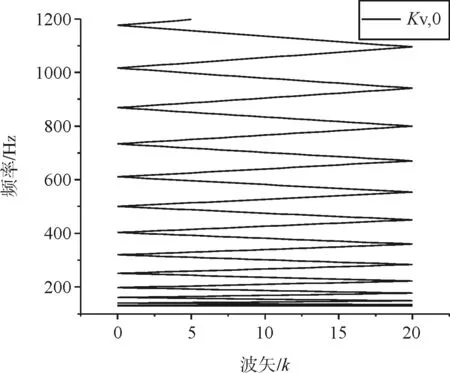
(a)Kv=Kv,0

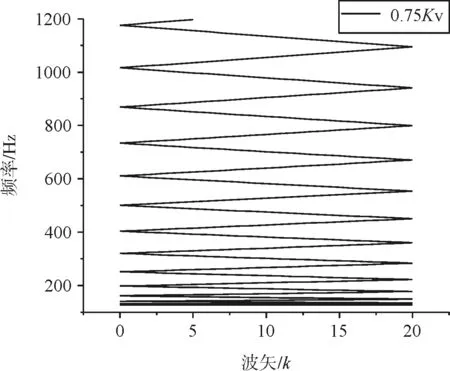
(b)Kv=0.75Kv,0

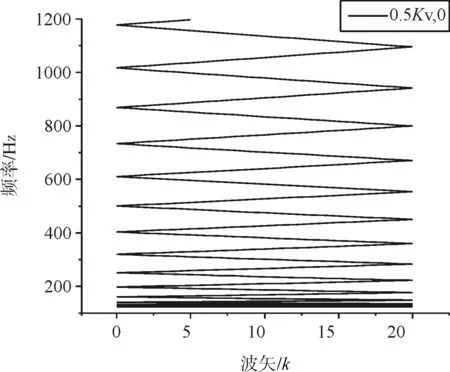
(c)Kv=0.5Kv,0

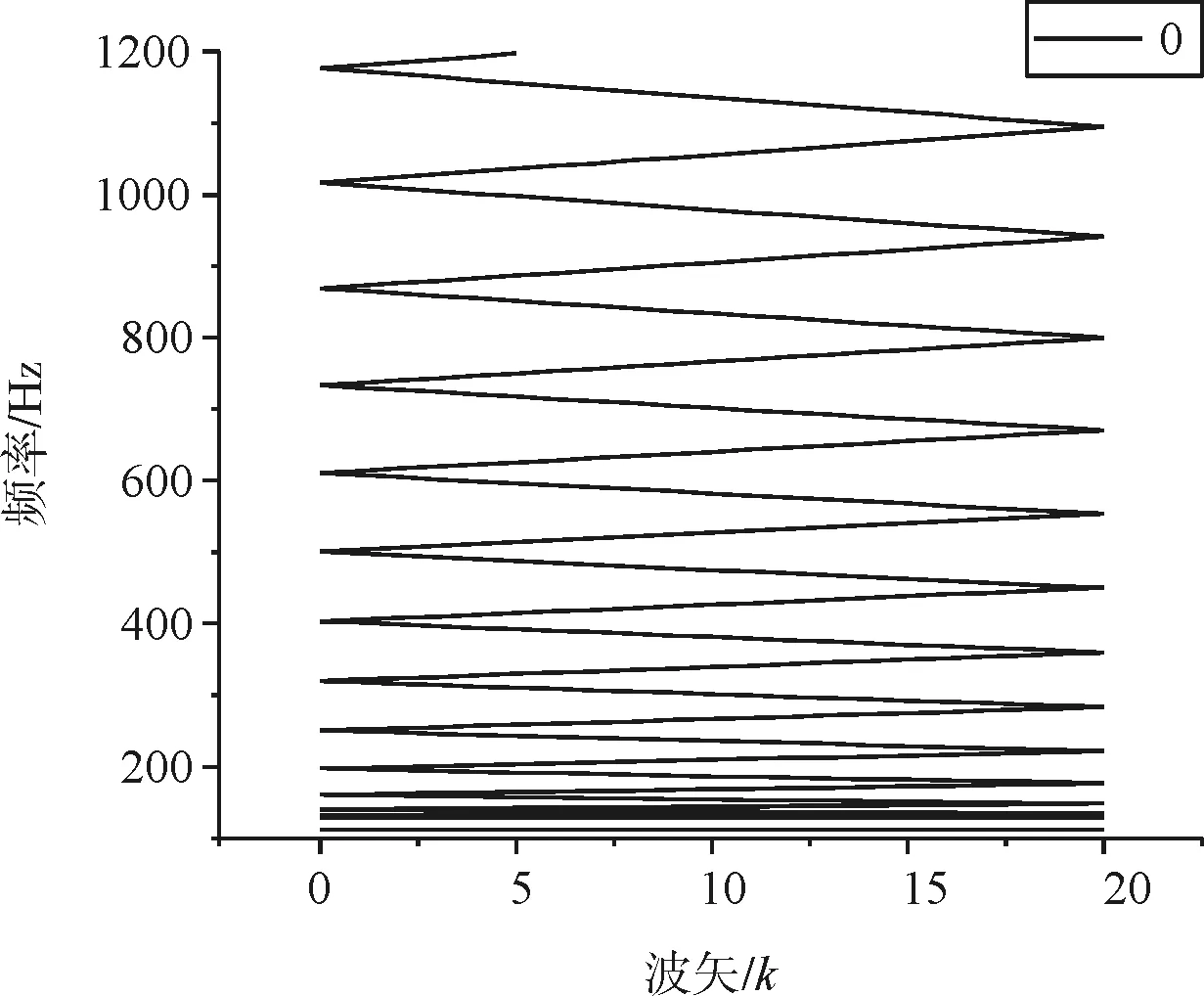
(d)Kv=0图5 垂向振动能带结构曲线

由图5可知，在不同Kv值下，130～1 200Hz范围内垂向振动都有对应的波矢，相应的振动能正常传递，这种振动不受抑制的频带即为通带。在0～130Hz范围内的能带曲线比较密集，现分别对图5(a)～图5(d)在0～13Hz频段内进行局部放大，如下图6(a)～图6(d)所示。

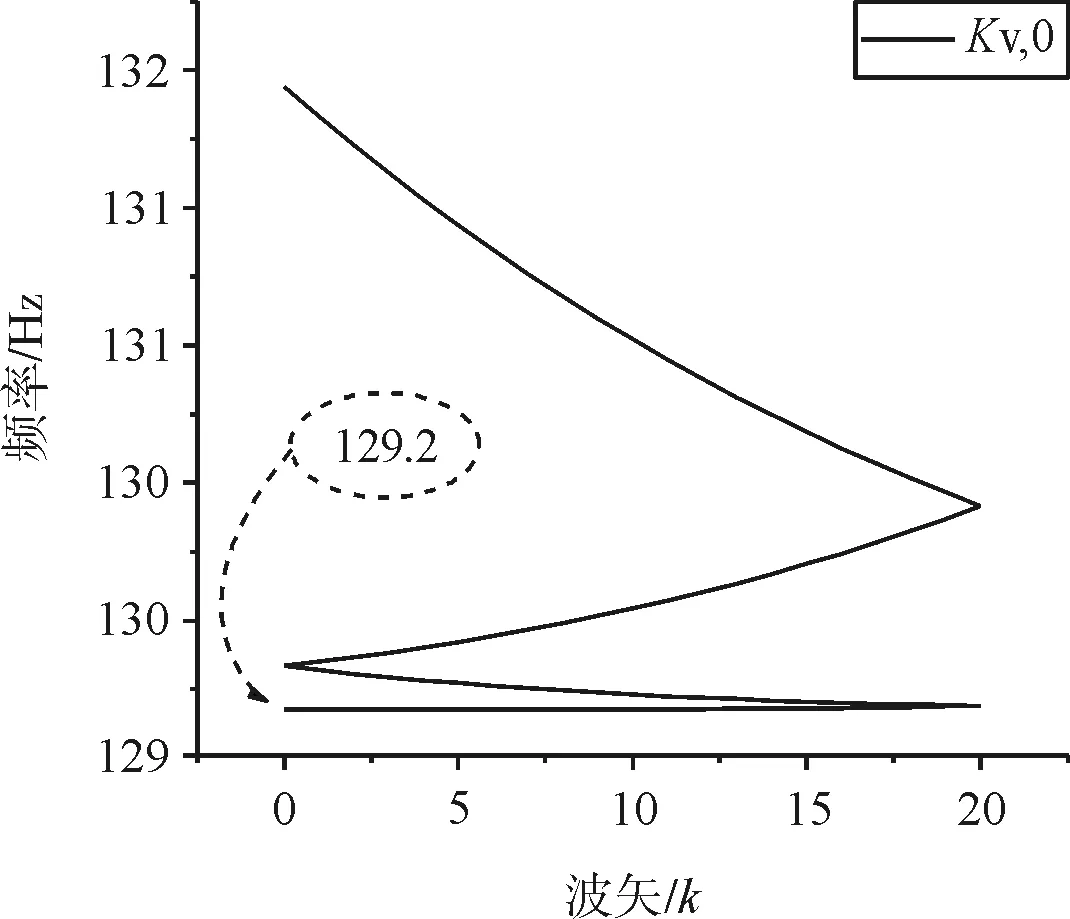
(a)Kv=Kv,0

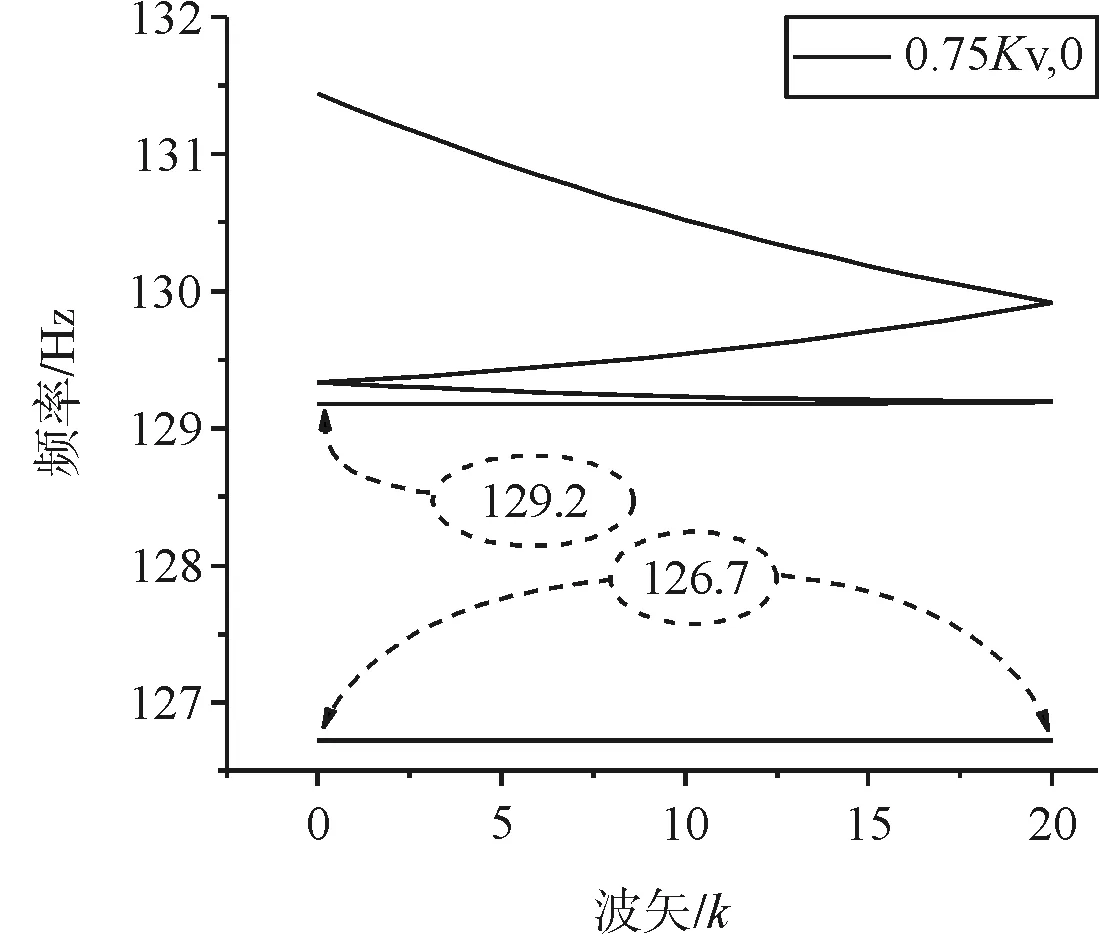
(b)Kv=0.75Kv,0

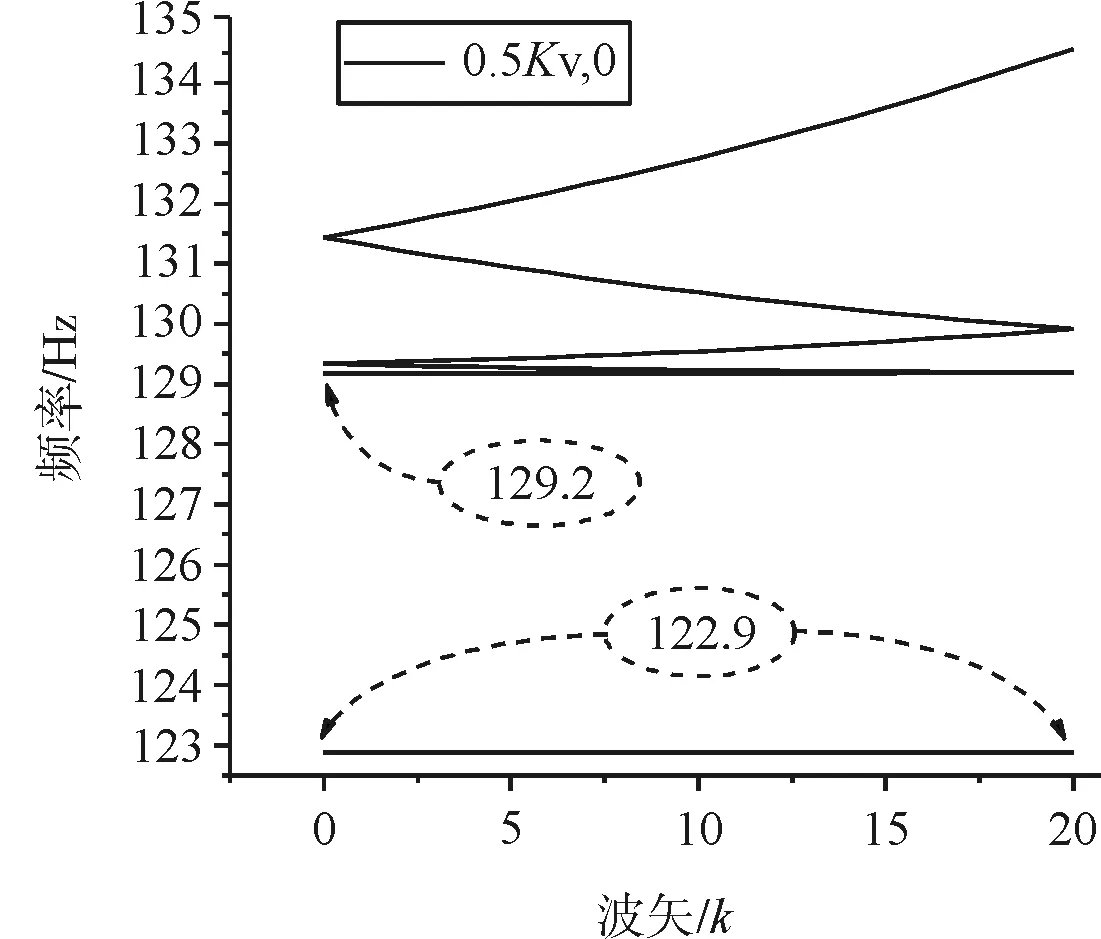
(c)Kv=0.5Kv,0

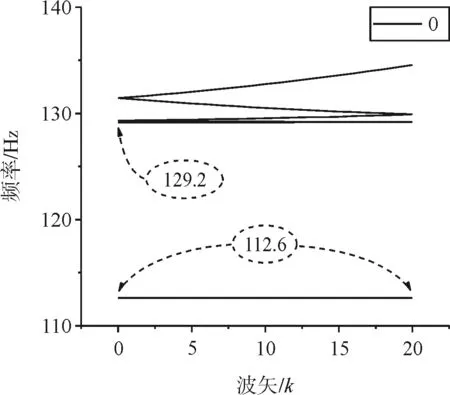
(d)Kv=0图6 0～130 Hz频带内局部放大

将图6中的带隙及缺陷态频率汇总如表2所示。

当Kv=Kv,0时，为严格周期结构，对应图6 (a)，可知在0～129.2Hz频带内，垂向振动没有对应的波矢k，说明此频带范围内的垂向振动波在结构中无法传播，这个频带称为带隙，与通带相对应，也被称作禁带。这个结果与文献[1]结果一致，证明有限元法结合超元胞算法的正确性。从图6(b)～图6(d)可知，不同扣件下都存在0～129.2Hz的带隙，但是在带隙内，还有一个平直带，此即为缺陷态，当缺陷处扣件刚度从0.75Kv,0变化至0时，该固定频率从126.7Hz降到112.6Hz，说明这个特定频率的振动是因为受损扣件刚度变化而引起的，且随刚度的减小而减小。观察能带曲线的带边频率振型以及缺陷态频率振型(图7)。

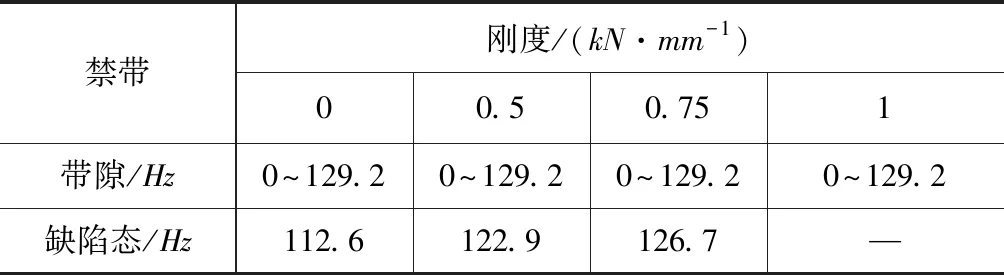
表2 扣件刚度参数

(a)带边振型

(b)缺陷处振型图7 振型示意

从图7(a)可知，带边频率处表现为钢轨整体的垂向平移振动，在缺陷态频率处，钢轨的振动被局域化在受损扣件附近，这种局域化会使原本受损的扣件产生较大的振动，加速受损扣件的破坏失效。

在带隙之外的能带曲线与无缺陷时基本一致，说明振动正常传播，在通带范围内的阵型如下图所示，扣件缺陷并没有对阵型产生明显的影响。

2.2 改变纵向刚度

与垂向刚度一样，将纵向刚度KL分成4个值，依次为KL,0、0.75KL,0、0.5KL,0和0。

由图8可知，纵向振动带隙为0～71Hz，改变扣件纵向刚度对纵向振动的带隙特性没有影响，且没有出现缺陷态，这是因为钢轨本身纵向刚度比较大，扣件纵向刚度对钢轨纵向振动影响很小。此时的带边振型如图9所示，为钢轨的纵向伸缩振动。

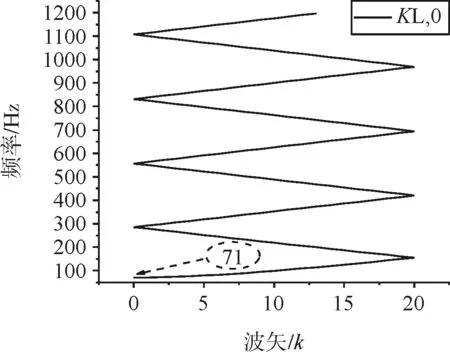
(a)KL=KL,0

(b)KL=0.75KL,0

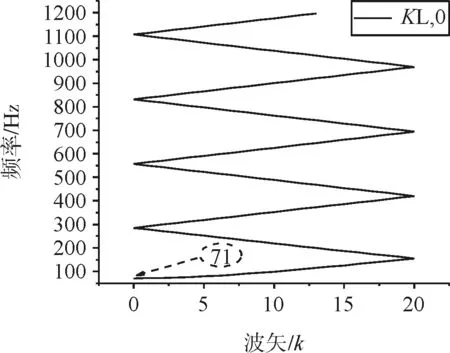
(c)KL=0.5KL,0

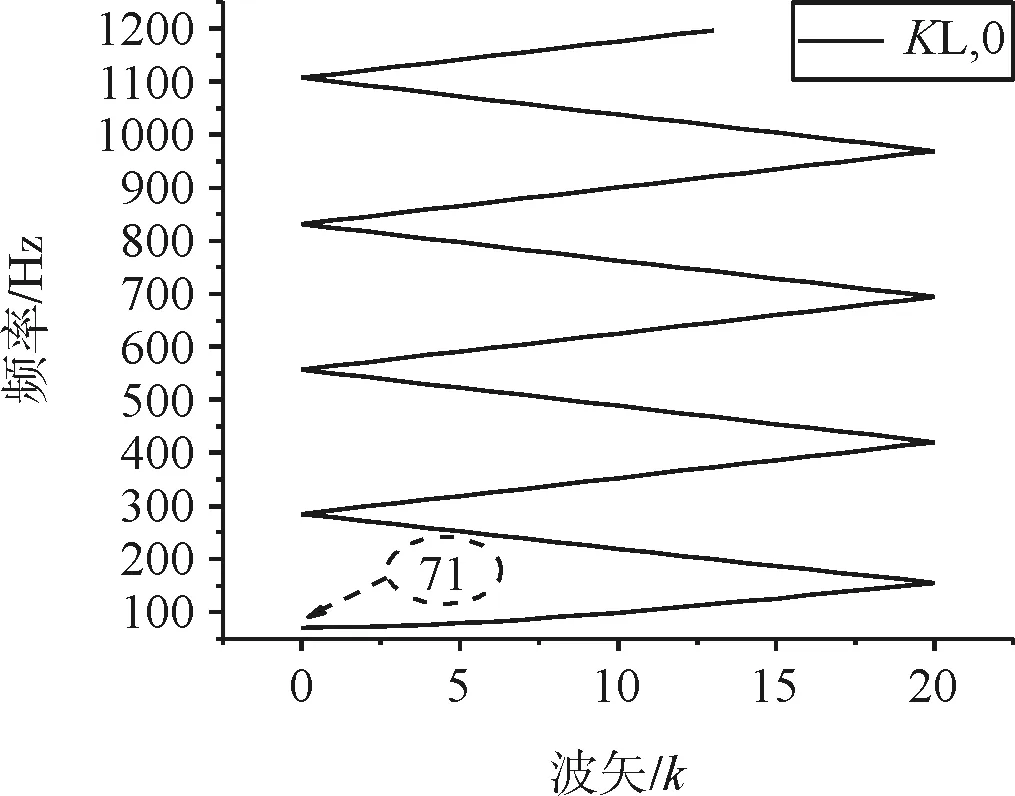
(d)KL=0

图9 带边振型

3 结论

通过有限元方法结合超元胞理论，建立30跨轨道结构有限元模型，并添加周期性边界条件，改变中间扣件垂向、纵向刚度来模拟扣件受损，从周期结构带隙特性理论的角度研究单个扣件受损引起的轨道结构缺陷对振动响应的影响。计算分析可得如下结论：

(1)周期性支撑的轨道结构在垂向和纵向振动方向上都存在带隙，且垂向振动带隙为0～129.2Hz，纵向振动带隙为0～71Hz。

(2)扣件垂向刚度减小会在垂向带隙内引起平直带，且平直带频率随着扣件垂向刚度的减小而减小，该平直带频率的振动波被局域在受损扣件处，会进一步加快受损扣件的破坏失效。

(3)改变扣件纵向刚度对纵向振动带隙无明显影响，且带隙内没有出现平直带。