无砟轨道钢轨振动传递频域特性试验分析

李泽宇， 谭 義

(西南交通大学土木工程学院，四川成都 610031)

伴随着国民经济的发展和人们出行需求的增长，列车的运行速度不断提高。无砟轨道作为新一代的轨道形式，要承担起承载更快、更重的列车的任务。由于轮轨相互作用愈加激烈，钢轨振动成了一个不可忽视的因素。这种振动信号会沿着钢轨向长度方向传播，也会沿着轨道结构往下传递[1]。钢轨的振动会对人们的生活环境产生危害，更会严重影响行车安全，使得维修任务加剧，而这些危害与钢轨的振动频率和传递特性息息相关，因此对无砟轨道钢轨振动沿着钢轨方向的传递特性的试验分析是十分必要的。

1 时域与频域分析法

1.1 时域分析法

时域是刻画物理信号对时间的关系，为了表达物理量随时间的变化规律。在时域图内对信号进行过滤波形、放大、统计特征的相关计算、相关性分析等处理，统称为时域分析法。

1.2 频域分析法

频域是一种描述信号在频率方面特性的坐标系。时域分析有许多局限性，如有些信号在时域上的特征不明显，因为信号不仅与时间有关，还与频率、相位等信息有关，这就需要进行信号频率的分析，频域分析可以将收录来的复杂信号分解为简单正弦波的叠加，可以更加精确地分析信号内部组成[2]。

把时域变换为频域的手段就要涉及到傅里叶级数和傅里叶变换。本实验运用MALTAB中的FFT函数进行频谱分析和PSD函数进行关于能量的功率谱分析[3]。

2 数据采集软件设计

本实验利用可视化的LabVIEW图形编辑语言和NI MAX配置管理软件交互设计数据采集软件设计。

本次实验设置8个通道，所以会生成8个AI加速计，将加速计中的灵敏度、最值、物理通道还有采样速率和采样数进行输入化，变为输入控件，就可以在前面板进行键入(图1)。

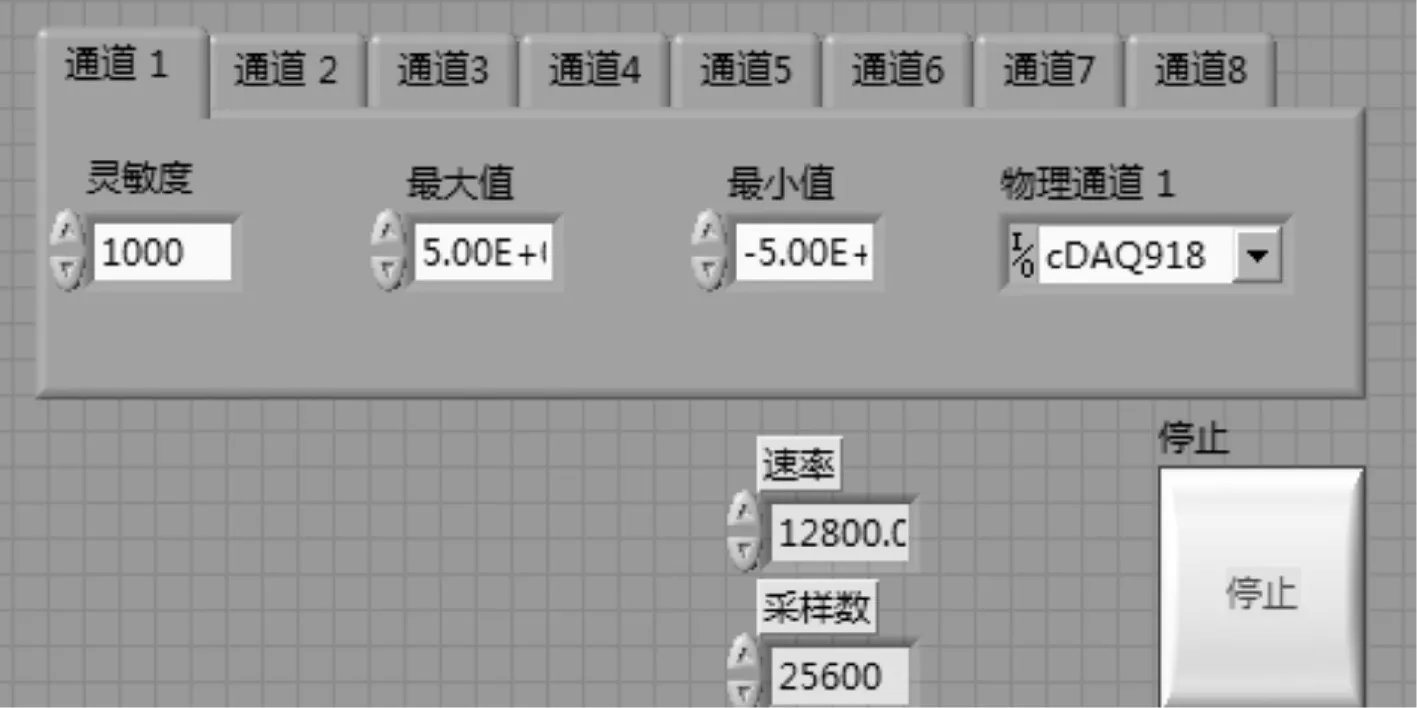
图1 LabVIEW键入参数的设置界面

最后设计好后的程序如图2所示。

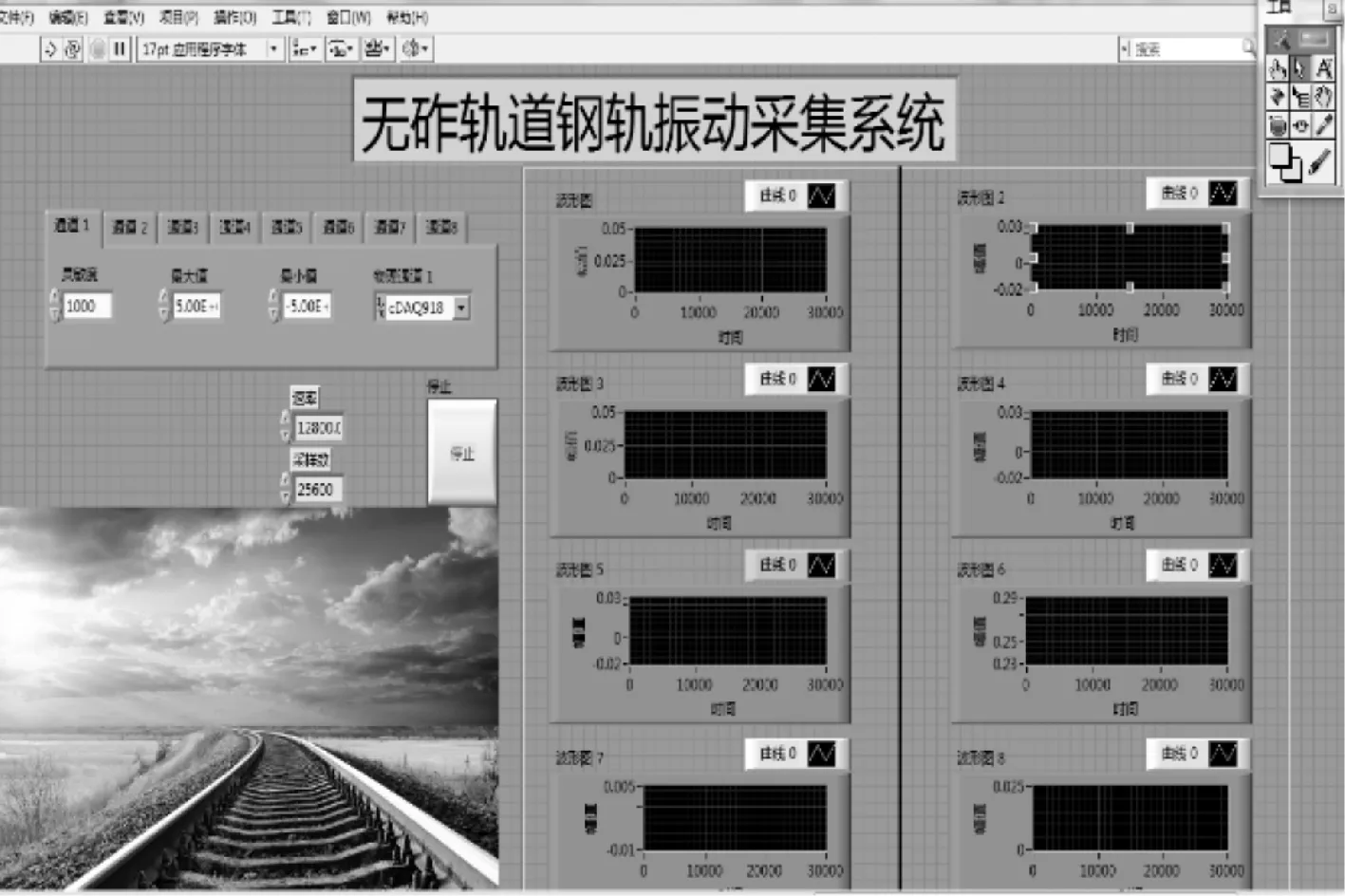
图2 LabVIEW钢轨振动采集系统界面前面板

本实验有7个三向加速度传感器，一个单向加速度传感器。沿着钢轨方向均匀布置8个测点，每70 cm一个测点，利用其中三项加速度传感器可同时测出3个互相垂直的方向的加速度，因此引出线有X、Y、Z三个方向，本实验采用的是Z接线头。

3 实验结果分析

3.1 频域分析

研究轨道钢轨垂向振动沿着纵向传的规律，首先通过频谱图对其进行频率特性的分析[4]。进行振动试验时，本实验通过一个敲击使钢轨产生振动，相当于给钢轨一个脉冲，这样在一个脉冲下的频谱图可以更直观地看出峰值的变化规律。取5个敲击点的数据，将数据转化为5个频谱图(图3)。由上而下分别是距离钢轨由近到远的5个测点的频谱图。

图3 五个测点的振动频域

3.1.1 振动传播峰值分析

由图3可以直观地看出，钢轨在发生振动时，频率峰值基本都出现在0～10 Hz，钢轨此时基本处于低频振动。

再取0～10 Hz作为主要频域进行研究，画出这5个测点的频率峰值的变化图(图4)。

图4 5个测点峰值的变化

从图4可得：在0～10 Hz的振幅峰值分别为：0.670 9g、0.026 8g、0.024 83g、0.002 467g、0.002 142g。从第一个测点一直到第5个测点的振动峰值一直在递减。由衰减率公式：(前一点峰值-下一测点峰值)/前一测点峰值，可以求出在传递过程中的衰减率[5]。

通过表1可得，峰值的变化趋势与理论上是一致的，一直处于衰减状态。并且，衰减率的变化是具有周期性的，测点1～2距离敲击点较近，振动峰值在这段传递过程中有明显的衰减，当衰减到一定幅值后，衰减达到一定的极限。从测点2～3可以看出，这时衰减率明显降低，之后，振动接着传递，衰减率又会有一个大幅度提升，测点3～4的衰减率达到了90.1 %。然而测点4～5的峰值衰减率随着振动传播有下降到了13.2 %，并且可以发现，从第4个测点附近往后顺延，峰值基本趋于0，维持在小数点后三位个数的加速度，这时振动幅值已经很小，环境噪声可能对其产生不可忽略的影响。由此可以得出结论：振动峰值衰减率并不是一成不变的，也不是逐渐变大或变小的，它存在一定周期性变化。

表1 测点之间的峰值衰减值及衰减率

3.1.2 振动峰值所对应的频率的变化规律

在对频谱图进行分析时，由于峰值均出现在0～10 Hz内，将频谱图放大为横轴最大值为10 Hz的频谱图，这样可以直接通过结合5个测点的振动峰值图直接求出峰值所对应的频率。放大后的频谱图见图5。峰值所对应的频率见表2。

图5 0～10 Hz的频谱图放大

表2 5个测点0～10 Hz的振动峰值及对应的峰值

通过表2可得，敲击所产生的振动对于前3个测点均在0.878 9 Hz时达到振动的峰值，所对应的峰值虽然是减小的趋势，但是还没有达到10-3的数量级。此时，敲击振动产生的振动响应占据主导地位，所产生的频率也是此时钢轨的主要频率。而到了4、5测点，峰值频率明显降低，此时的峰值数量级有一个大幅度下滑，已经到了10-3的数量级。这是因为当敲击振动传递到4、5测点时，由于振动的衰减，导致敲击产生的振动频率在该处并不能占据主导地位，而此时环境噪声所产生的振动会干扰到振动信号，降低峰值频率。因此，可得结论：当距离振动源较近时，峰值频率以敲击振动的频率作为主要频率，并且以0.878 9 Hz保持不变，当传递距离较远时，振动信号的衰弱、噪声的影响会降低峰值频率。

3.2 功率谱分析

研究无砟轨道钢轨垂向振动沿着钢轨方向振动的能量传播规律，通过功率谱图进行分析。

对已有的5个测点的数据绘制为功率谱图。由于发生振动的主频率集中在0～10 Hz，把图放大到0～10 Hz范围内进行研究。第一个测点到第五个测点的功率谱图分别如图6～图10。

图6 测点1的功率谱图

图7 测点2的功率谱图

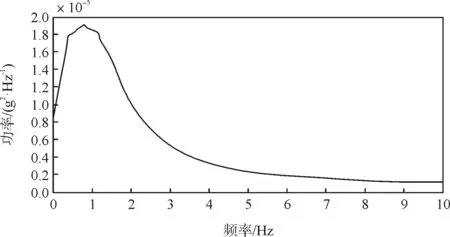
图8 测点3的功率谱图

图9 测点4的功率谱图

图10 测点5的功率谱图

3.2.1 振动传播中能量分布规律

功率谱图代表了能量的分布状况，从图中，可以明显的看到，峰值发生的地方能量较高。我们所研究的5个测点的峰值功率谱密度及对应的频率值见表3。

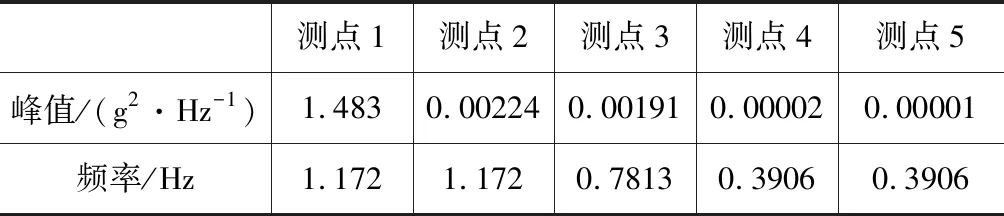
表3 5个测点的功率谱密度峰值及发生频率表

对表3分析，前两个测点峰值发生频率保持不变，也就是说能量的主要分布在频率为1.172 Hz的频率范围附近，当振动传播到第3个测点时功率密度峰值有明显降低，随后的4、5测点的功率密度峰值频率又稳定在0.390 6 Hz。这表明，第三个测点是一个能量分布的规律转折点，因为前后的峰值频率均发生了跳跃。故此分析，第三个测点附近会产生对能量在频率方面的重分布，这种重分布前后的能量分布基本处于稳定，例如本次实验前后的1、2测点和4、5测点，分别稳定在1.172 Hz和0.390 6 Hz。

另外，从表中曲线的光滑度可得：距离敲击点较近的1～3测点的功率密度曲线都较为平滑，这是因为，前三个测点中的振动主要是由于敲击产生的，故此功率谱密度值也普遍偏高，可以通过功率谱密度峰值可以看出，当振动传播到4、5测点时，功率谱密度峰值跌到了10-5和10-6的数量级。并且，4、5测点的功率密度曲线明显变得不光滑、曲折。这是因为在振动传播到4、5测点附近时，敲击产生的振动影响已经变得微弱了，噪声及其他振动对能量分布有较为明显的影响。

3.2.2 振动传播过程中能量的衰减

对已经得到的5个测点的功率谱图进行面积计算，得到的值就是在该频率范围内每个测点所产生的能量值。由于振动主要发生在0～10 Hz频率范围内，所以主要研究0～10 Hz范围内的频谱图，通过计算其面积求得的能量就是0～10 Hz范围内5个测点的能量值。5个测点的能量值见表4。

表4 5个测点的振动能量

通过表4不难发现，测点1的振动能量最大，这是因为它距离敲击点很近，能量还没有衰减太多，从测点1～2过程中，能量有大幅度损失，然而到了测点2～3能量基本维持不变，缓慢减少，测点3～4能量又有明显的跌落，但是减少量并没有1～2的大。

通过计算能量衰减率可以更好地看出能量的变化趋势。能量衰减率=(前一测点振动能量-后一测点振动能量)/前一测点振动能量。测点1～2、2～3、3～4、4～5的能量衰减率见表5。

表5 各测点间的能量衰减率

通过表5可得，从测点1传播到测点2的时候，振动能量基本完全损失，衰减率高达99.8 %，结合对于频域峰值的分析。也就是说，在测点1～2这一阶段中，带有主要能量的频率振幅发生了很大的衰减，但是这种衰减并没有改变频谱图密度峰值的位置，它属于一种整体的衰减。观察测点2～3，频率衰减率相对于1～2有显著降低，这是因为大部分的易损耗的振动能量已经在测点1～2的振动过程中损失，而留下来的大部分振动信号会在2～3测点之间保持一段长度的能量传播。测点3～4过程中，上一阶段已经保持了一段长度的振动信号会再次做一个大幅度衰减，类似距离敲击点近的1～2过程的大跌落。测点4～5的过程中，能量还处于衰减状态，这表明振动信号仍然在传播，但是由于4、5测点的振动能量很低，并且只有7.2 %的衰减率，可以认为能量基本衰弱完成，趋于稳定。

结果表明，振动在沿钢轨纵向传递时，能量并不是线性衰减的，而是有一定的衰减规律的。每到一定的距离能量会产生一次跌落，是一种梯度变化式的衰减过程。

4 结束语

(1)钢轨产生振动时，其频域图中振动峰值的变化趋势与理论上是一致的，一直处于衰减状态，且衰减率呈周期变化。由振动源向远处延伸，所对应的振动峰值虽然是减小的趋势，但是峰值频率不会发生变化。在距离敲击点280 cm左右处，敲击振动产生的振动响应均占主导地位，所产生的频率也是此时钢轨的主要频率。当传播到360 cm处，峰值频率明显降低，并且峰值会有大幅度衰弱，此时环境噪声对于远端的振动影响不可以忽略。

(2)钢轨产生振动时，距离敲击点较近的功率谱密度峰值发生频率保持不变，这段距离的范围在140 cm左右，也就是说能量主要分布都在相同的频率范围内。当振动在140～280 cm范围内传播时功率密度峰值会有明显降低。在280～420 cm范围内，能量进行重新分布，在这之后的能量分布规律又会在420 cm后保持稳定。对于能量衰减，振动在沿钢轨纵向传递时，能量并不是线性衰减的，而是有一定的衰减规律的。每到一定的距离能量会产生一次跌落，是一种梯度变化式的衰减过程。